改进蚁群算法的飞机冲突解脱路径规划方法*
2016-06-24敬忠良李旻哲
倪 壮, 肖 刚, 敬忠良, 李旻哲
(上海交通大学 航空航天学院,上海200240)
改进蚁群算法的飞机冲突解脱路径规划方法*
倪壮, 肖刚, 敬忠良, 李旻哲
(上海交通大学 航空航天学院,上海200240)
摘要:冲突解脱是空中交通防撞系统中一个关键问题。提出了一种基于改进蚁群算法的冲突解脱路径规划方法。该方法通过优化蚁群算法初始搜索角度,减少了盲目搜索的时间。此外,在搜索过程中引入“精英策略”,对当前时刻寻找的最优解给予额外的信息素增强,使得算法的搜索具有一定的方向性,从而得到更优的规划路径,缩短算法的搜索时间。通过仿真验证,改进后的算法可以得到更优的冲突解脱路径,算法效率更高,在空中交通防撞系统中具有较好的发展前景。
关键词:空中交通防撞系统; 冲突解脱; 蚁群算法; 精英策略; 角度信息
0引言
空中交通防撞系统(trafficalertandcollisionavoidancesystem,TCAS)是飞机环境监视系统(aircraftenvironmentsurveillancesystem,AESS)的一个重要组成部分。冲突解脱是TCAS中十分重要的一个模块,主要功能是当预测到两架或多架飞机发生冲突时,为飞机规划出一条避免飞行冲突的理想路径。近年来,在冲突解脱方面已经有了大量的研究工作,例如:神经网络法[1]、遗传算法[2]、人工势场法[3]等。神经网络法的学习能力很好,但当动态环境中障碍物较多时,网络结构庞大且神经元的阈值需要随时间的变化而不断改变;遗传算法的全局搜索能力很好,但搜索的空间大,并且当环境改变时必须重新建立模型;人工势场法虽然便于底层的实时控制,但缺乏全局信息,可能会出现局部最优值的问题。
蚁群优化[4](antcolonyoptimization,ACO)算法,又称蚂蚁算法,是一种用来寻找优化路径的几率型算法。它由DorigoM在1992年提出,其灵感来源于蚂蚁在寻找食物过程中发现路径的行为。蚁群算法作为一种自组织算法,具有良好的扩展性、较强的鲁棒性、算法实现也较简单,使得该算法在解决旅行商问题(travelingsalesmanproblem,TSP)[5]、函数优化[6]和路径规划[7,8]等问题都取得了较好的实验结果。但是,传统的蚁群算法的搜索效率受参数的设置影响很大,并且会出现收敛速度慢,陷入局部最优等情况。针对这些情况,国内外学者做了不少工作。StutzleT等人提出了一种最大最小蚂蚁系统算法[9],以防止早熟收敛现象的发生,但当信息平均分布在各个方向上时,蚂蚁释放的信息素将对蚁群的决策产生误导。BoteeHM利用遗传算法对蚁群算法参数的组合优化进行了深入的研究[10],但遗传算法计算量大,优化效果不明显。
针对上述出现的问题,本文通过对多架飞机冲突解脱问题的建模,引入飞行的角度信息,对蚁群算法初始时刻的搜索范围进行了约束,同时,在每次循环结束后即对当前时刻寻找的最优解给予额外的信息素增强,提出了一种基于改进的蚁群算法的冲突解脱算法。由于该算法在搜索过程中有一定的方向性,又避免了初始阶段的盲目搜索,使得运算效率和系统的实时性得到了提高。
1理论背景
1.1蚁群算法的数学模型
(1)
式中τij(t)为城市i与城市j连接路径上在t时刻的信息素浓度;ηij(t)为启发函数,表示蚂蚁从城市i转移到城市j的期望程度;α为累积信息重要程度因子,β为启发函数重要程度因子;allowedk(k=1,2,…,m)表示蚂蚁k下一步允许访问城市的集合。
传统蚁群算法中,启发函数ηij(t)为
ηij(t)=1/dij
(2)
式中dij为城市i与城市j间距离。
当所有蚂蚁完成一次循环后,各个城市之间连接路径上的信息素浓度需要进行实时更新,多路径的选优计算公式为
(3)


(4)
式中Q为信息素浓度的常数;Lk为蚂蚁k在本次循环中所走路径的长度。
1.2改进蚁群算法
文献[11]提出了一种改进的蚁群算法,引入了精英策略(elitiststrategy),它的基本思想是: 在每次循环结束后即对当前时刻寻找的最优解给予额外的信息素增强,使其在下一时刻循环中对蚁群更加具有吸引力。信息素根据下式进行更新
τij(t+1)=(1-ρ)τij(t)+ρΔτij(t)
(5)
(6)
式中Q为信息素浓度的常数,Lbest为最短路径,Lworst为最长路径,ρ为蒸发因子,Δτij(t)为城市i到城市j蚂蚁所引起的信息素的增加量。
如式(6)所示,更新后每条边的信息素限制在所经过的最长路径信息素浓度和最短信息素浓度之间,避免某些边上的信息素过大。该算法减小了各条边信息素的差距,扩大了解的搜索空间,可以防止算法过早陷入局部收敛。
此外,由于蚁群算法一开始没有一个确切的路径,搜索时间大多消耗在搜索的初始阶段。针对该情况,文献[12]提出了一种新的改进的蚁群算法,解决了搜索算法初始阶段没有明确的方向导致的盲目搜索的问题,缩小了搜索范围,减少了搜索时间,提升了算法效率。
假设城市r信息素初始值为
(7)
式中W为常数,Lp,r为起始城市p到城市r间的距离,Lr,q为城市r到目的城市q间的距离。由于W为常数,当Lr较小时,τr(0)较大。通过比较L的大小确定算法在初始阶段大致的搜索方向。
2建模与分析
2.1冲突解脱问题建模


(8)

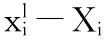
(9)
所以,冲突解脱问题就是找到解脱路径,使n架飞机的延误距离之和最小。在时刻t,任意两架飞机i和j之间的距离满足

(10)
式中δ为空管所规定的在水平空域中飞机之间必须保持的安全距离,一般取5海里。
2.2问题分析
假设飞机的起始点为S,终点为D,两点间距离为L,飞机解脱角度为θ,最小解脱角度为θ0。场景如图1所示。
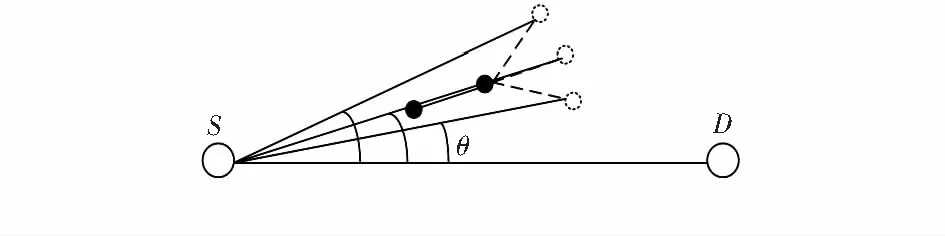
图1 飞行场景角度示意图Fig 1 Angle chart of flight scene
为了使延误距离最小,显然在满足式(10)的约束条件下,优先选择较小的角度θ。所以,在使用蚁群算法搜索最优路径的初始时刻,应当首先计算解脱路径与原航线的偏离角度,从较小的路径角度开始搜索。同时,根据“精英策略”,在搜索过程中应当动态更新下一时刻路径与原航线的角度,在每次循环结束后即对当前时刻寻找的最优解给予额外的信息素增强,使其在下一时刻循环中对蚁群更具吸引力。
2.3冲突解脱算法
根据以上分析,本文基于改进的蚁群算法,给出了飞机在冲突解脱时的最优路径搜索算法。算法流程如图2所示。

图2 改进蚁群算法的算法流程图Fig 2 Flow chart of the improved ant colony algorithm
改进的蚁群算法具体算法步骤如下:
1)初始化参数,初始化改进蚁群算法的最大迭代次数NCmax,蚂蚁数量m、起始点为S,终点为D;
2)将各只蚂蚁随机的放置在n个不同的出发点(代表n架飞机的初始出发点),在搜索初始阶段加入角度的信息,指导所有的蚂蚁走完路径;
3)根据不同路径的蚂蚁之间的约束条件式(10)来约束蚂蚁在路径中的行为,确保蚂蚁在行走的过程中无冲突发生;
4)计算每个蚂蚁到终点后与初始目标点的距离,由式(9)来计算最优化目标函数的值,记录并选择当前迭代次数中的最优解,同时给予最短路径较大的信息素增强,对各路径上的信息素浓度进行更新;
5)如果迭代次数没有达到最大,则清空蚂蚁经过路径的记录,返回步骤(2);否则,计算终止,输出最优解。
3实验结果与分析
假设在一块200km×200km的空域范围内,初始时刻出现4架飞机,飞机匀速飞行,起点分别位于[0,100],[100,200],[200,200],[200,0]km四个点,目标终点为[200,100],[100,0],[0,0],[0,200]km。目标飞行20步,并在第10步4架飞机会同时发生冲突。将改进后的蚁群算法与原始的蚁群算法进行对比,实验中选取的蚂蚁总数m=80 只,ρ=0.35,Q=1000,迭代次数NCmax=200。本文通过Matlab对原始蚁群算法和改进后的蚁群算法进行仿真,图3为原始蚁群算法规划出的冲突解脱仿真结果,图4为改进蚁群算法规划出的冲突解脱仿真结果,图5为原始蚁群算法与改进后的蚁群算法的延误路径总长度曲线图,表1为原始蚁群算法与改进后的蚁群算法的平均运行时间表。
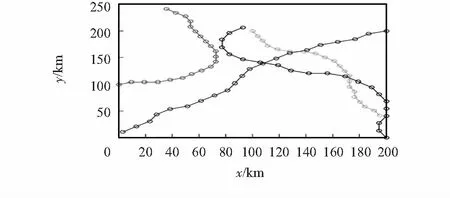
图3 原始蚁群算法仿真结果Fig 3 Simulation results by original ant colony algorithm

图4 改进后蚁群算法仿真结果Fig 4 Simulation results by improved ant colony algorithm
通过观察可知,本文提出的改进蚁群算法规划的路径更接近于原有航线,延误路径总长度更小,在解脱的同时能尽量按原航线方向飞行,使得解脱后的飞行路线更优。此外,本文提出的改进蚁群算法的算法效率,运行时间都明显优于原始蚁群算法,平均运行时间缩短了约35.5 %。仿真结果证实了改进的蚁群算法能有效地解决多架飞机间冲突解脱路径规划问题。
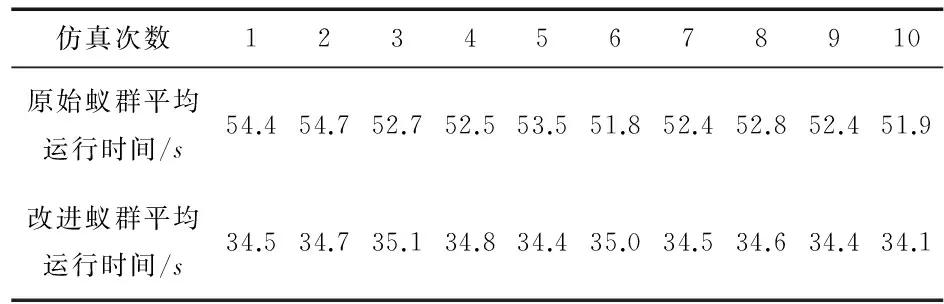
仿真次数12345678910原始蚁群平均运行时间/s54.454.752.752.553.551.852.452.852.451.9改进蚁群平均运行时间/s34.534.735.134.834.435.034.534.634.434.1
4结束语
本文提出了运用改进的蚁群算法对多架飞机间冲突解脱进行路径规划的方法。传统的蚁群算法搜索效率较低,本文引入了“精英策略”, 对当前时刻寻找的最优解给予额外的信息素增强,使得算法在搜索过程中具有一定的方向性,提升了算法搜索效率;此外,在算法搜索的初始阶段引入了角度信息,避免了初始阶段的盲目搜索,缩短了算法的搜索时间。最后利用改进的蚁群算法实现了飞机间冲突解脱进行路径规划,仿真实验证明了该路径规划方法的有效性与可行性。
参考文献:
[1]邓万,郑庆,陈琳,等.神经网络急速学习方法研究[J].计算机学报,2010,33(2):279-287.
[2]刑焕来,潘炜,邹喜华.一种解决组合优化问题的改进型量子遗传算法[J].电子学报, 2007,35(10):1999-2007.
[3]DerekJBennet,ColinRMcInnes.Distributedcontrolofmulti-robotsystemsusingbifurcatingpotentialfield[J].RoboticsandAutonomousSystems,2010,58(3):256-264.
[4]DorigoM,ManiezzoV,ColorniA.Antsystem:Optimizationbyacolonyofcooperatingagents[J].IEEETransactionsonSystems,Man,andCybernetics—PartB,1996,26(1):29-41.
[5]郭平,鄢文晋.基于TSP问题的蚁群算法综述[J].计算机科学,2007(10):181-184.
[6]马卫,朱庆保.求解函数优化问题的快速连续蚁群算法[J].电子学报,2008,36(11):2120-2124.
[7]段爱民,陈泽琳.基于改进蚁群算法的物流配送路径优化[J].计算机技术与发展,2011(12):178-181.
[8]郑峰峻.改进的蚁群算法在物流配送路径问题中的实现[J].物流科技,2010(2):22-24.
[9]StutzleT,HoosHH.Max-minantsystemandlocalsearchforthetravellingsalesmanproblem[C]∥IEEEInternationalConferenceonEvolutionaryComputation,Indianapolis:IEEE,1997:309-314.
[10]BoteeHM,BonabeauE.Evolvingantcolonyoptimization[J].CompexSystem,1998,1(2):149-159.
[11] 张家善,王志宏,陈应.一种基于精英策略的改进蚁群算法及应用[J].计算机系统应用,2012,21(10):105-108.
[12] 叶仕通,万智萍.一种基于改进全局信息素更新效率的蚁群算法及仿真[J].计算机应用与软件,2014,31(1):176-179.
[13] 郭茜.空中交通飞行冲突解决方法研究[D].天津:中国民航大学,2008:36-40.
Pathplanningmethodforaircraftsconflictresolutionbasedonimprovedantcolonyalgorithm*
NIZhuang,XIAOGang,JINGZhong-liang,LIMin-zhe
(SchoolofAeronauticsandAstronautics,ShanghaiJiaoTongUniversity,Shanghai200240,China)
Abstract:Conflict resolution is one of key issues of traffic alert and collision avoidance system (TCAS).A path planning method for conflict resolution based on an improved ant colony algorithm is presented.The proposed method initializes ant colony optimization algorithm with the angle information to reduce blind search time."Elite" strategy is also introduced which can provide additional pheromone enhanced during search procedure for the optimal solution.This scheme accelerates the algorithm searches with a suitable direction,which results in better planning path,shortens search time.The simulation results show that the proposed algorithm derives better path for conflict resolution with a higher efficiency,and has good prospects for development in air traffic collision avoidance system.
Key words:traffic alert and collision avoidance system(TCAS); conflict resolution; ant colony algorithm; elite strategy; angle information
DOI:10.13873/J.1000—9787(2016)04—0130—04
收稿日期:2015—07—15
*基金项目:国家自然科学基金资助项目(61175028)
中图分类号:V 271.1
文献标识码:A
文章编号:1000—9787(2016)04—0130—04
作者简介:
倪壮(1989-),男,安徽淮南人,硕士研究生,主要研究方向为空中交通防撞系统。
