多面棱体的时栅转台自动标定系统设计*

王淑娴， 彭东林,2， 高忠华,2， 张旭云， 周金钢， 郑方燕,2

(1.重庆理工大学 机械检测技术与装备教育部工程研究中心,重庆 400054;2.重庆理工大学 时栅传感及先进检测技术重庆市重点实验室，重庆 400054)

多面棱体的时栅转台自动标定系统设计*

王淑娴1， 彭东林1,2， 高忠华1,2， 张旭云1， 周金钢1， 郑方燕1,2

(1.重庆理工大学 机械检测技术与装备教育部工程研究中心,重庆 400054;2.重庆理工大学 时栅传感及先进检测技术重庆市重点实验室，重庆 400054)

摘要:针对传感器安装偏心、使用环境变化等因素造成时栅转台精度降低的问题，提出了由多面棱体和自准直仪对误差进行标定，并利用谐波修正技术进行误差修正的时栅转台自动标定系统。系统以多面棱体和自准直仪高精度测量仪器作为测量基准，以ARM处理器为核心对步进电机进行闭环控制，实现转台的精确定位，且能够进行数据采集和误差处理。经实验证明：与手动标定方式相比，该标定系统不仅效率高而且标定后的时栅转台测量系统分度精度可达±1.3″。

关键词：多面棱体； 自准直仪； 时栅位移传感器； 转台； 自动标定

0引言

时栅位移传感器是一种采用“时空转换”的思维方式，用时间量去完成空间位移测量的新型传感器[1～3]。以时栅角位移传感器作为测量元件的时栅转台因精度高、成本低的优点，因而具有良好的应用前景，可广泛地应用于数控机床以及其他回转运动控制系统。但是由于受传感器安装偏心、使用环境的变化等因素的影响，转台的定位精度相比时栅传感器精度有较大的损失，导致机械加工精度降低。

为了解决上述问题，本文以多面棱体和自准直仪为基准仪器，以ARM为核心的数控系统对步进电机进行闭环控制来实现转台的精确定位。定位完成后上位机与下位机通信完成数据的自动采集并通过上位机程序进行误差处理，从而实现时栅转台的智能化高精度标定。

1自动标定系统

整个标定系统是由装有时栅的转台、多面棱体、自准直仪、数控系统和上位机组成。多面棱体随着转台的转动在数控系统的控制下进行转台准确定位，完成数据的采集，采集后的数据送入上位机完成误差处理。

1.1时栅位移传感器

在回转工作台中，转台转动的实际角位移是由高精度时栅传感器测量出来。时栅角位移传感器作为转台的主要测量元件其主要由定子、定子内嵌线圈、转子及定测头b和动测头a组成，如图1所示。

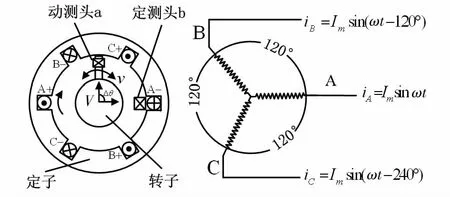
图1　时栅位移传感器的结构原理图Fig 1　Structure principle diagram of time-grating displacementsensor

定子内嵌线圈为空间上互差120°的三相绕组，工作时，在三相绕组中通入幅值相等，相位相差120°的激励电流

(1)

式中Im为激励电流振幅；ω为激励电流频率。

类似于交流电机，在定子气隙中产生一个以角速度V运动的旋转磁场M。旋转磁场M中放置定测头和动测头两测头，其中，定测头固定不动，动测头则以速度v随着转子转动，通过检测磁场M经过定测头b和动测头a的时间差ΔT和定测头信号的周期T，将ΔT和T这两个模拟信号经一系列的信号处理后送入微处理器进行计算处理，得到转子运动的角位移大小(单位为(°))

(2)

式中θ为角位移；V为磁场的运动速度；ΔT为时间差；T为信号周期；W为一个对极所对应的角位移量。

1.2多面棱体—自准直仪标定方法

如图2所示，将多面棱体和时栅角位移传感器安装在转台的主轴上，同时将自准直仪放置在可调整的固定三角架上。调节三角架的高度和自准直仪的位置，使自准直仪视轴和多面棱体工作面互相垂直，并和多面棱体工作面的中心在同一水平面上[4]。转动转台，使转台停留在0°～5°(72对极时栅的单对极内)位置。标定的过程中，当转台转到多面棱体面中心时，自准直仪获取距棱体面中心法线方向的偏差角，上位机软件程序根据多面棱体的面数加上偏差值计算出角度值，再结合采集到的时栅角位移值，从而实现对转台高精度标定。时栅转台各测点的误差值

li=ai-[(bi-b1)+Δc±di]

(3)

式子li为被校准时栅转台第i测点的误差值；ai为时栅转台第i个测点的示值，i=1,2，…，n;bi为棱体的第i面和第一面的夹角;Δc为多面棱体面的修正值；di为自准直仪的偏差值。

图2　多面棱体—自准直仪校准时栅转台Fig 2　Calibration time-grating turntable based on polygons-autocollinator

2系统设计

基于多面棱体和自准直仪的时栅转台自动标定系统的原理框图如图3所示。整个标定系统是由基准仪器(多面棱体和与它配套使用的自准直仪)、待标定的时栅转台、自动控制的核心数控系统和计算机组成。

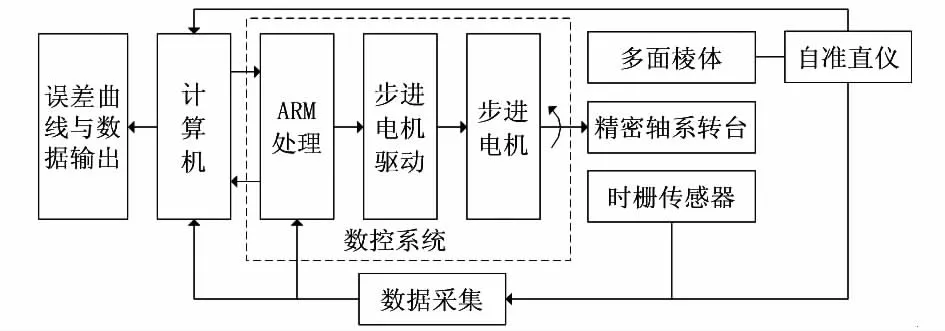
图3　实验系统原理框图Fig 3　Principle block diagram of experimental system

多面棱体安装在时栅转台的转轴上，步进电机驱动时栅转台匀速运动。转台旋转到自准直仪对准多面棱体中心时，对时栅传感器进行动态采样，并且这一采样序列反馈给ARM处理器形成对转台的全闭环控制。同时自准直仪采集到的信号为多面棱体面中心定位的偏差值，上位机程序将偏差值和多面棱体转过的角度数、修正值计算处理得到转台转过的真实角位移。转台转动的实际角位移和时栅转台的显示数据通过上位机作比较得到转台的原始误差，然后进行相应的谐波分析和实时显示等数据处理，并且利用谐波修正技术对误差进行修正。

2.1数控系统的设计

如图4所示的数控系统是时栅转台自动标定系统提高测试效率的关键部分。采用步进电机带动转台旋转取代了繁杂的人工摇转手轮带动转台旋转操作，上位机按照一定的控制算法控制步进电机带动转台定位取代了人眼观察对转台转动的定位。

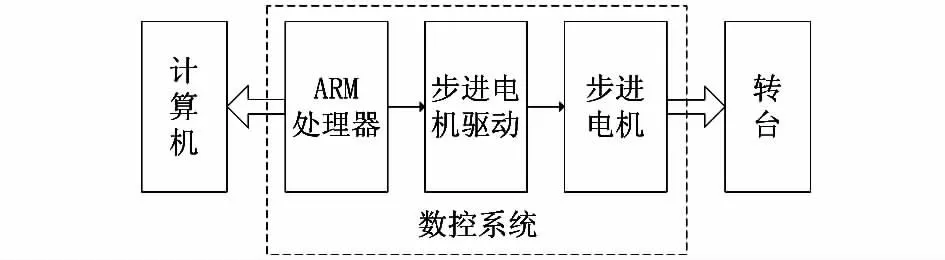
图4　数控系统的结构框图Fig 4　Structure block diagram of numerical control system

由于数控系统主要是通过ARM处理器对步进电机的闭环控制来实现对于转台的精确定位，因此,ARM的控制和步进电机的驱动是数控系统的重要环节。

2.2ARM控制与电机驱动

数控转台由步进电机驱动,以ARM处理器为核心控制步进电机的自动转位。首先调整数控转台转动至时栅传感器输出为0°，自准直仪对准棱体第一面，计算机通过串口开始采集时栅的角度值与自准直仪读取的偏差值，时栅传感器的输出信号由上位机发送给ARM处理器，ARM根据接收的信号控制步进电机的转动。同时，接收时栅的反馈值形成闭环控制，使转台的角度得到调整，最终实现精确定位。定位完成后，ARM处理器向计算机发送“定位完成”信号。

电机的驱动选用与其他驱动方法相比具有减小或消除电路中的低频振荡、噪声和转矩波动等优势的细分驱动方法[5]，将一个歩距角细分成若干小步来实现高精度的定位。采用MS—2H090M驱动器配合34HS300DZ型两相混合式步进电机。为了达到最高的控制精度，使用时将驱动器的细分值设为最大值200，步进电机1.8°的歩距角转换为0.009°的驱动脉冲当量Pd，分度转台的蜗杆和蜗轮副的传动比为Z=180∶1。因此，每个驱动脉冲当量ΔP为

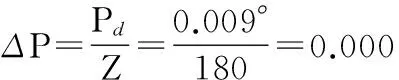
(4)

可以匹配多面棱体的精度，足够满足系统±2″的分度精度要求。

3软件设计

根据测控系统的任务要求，上位机程序需要实现采集自准直仪偏差值和时栅的数据和误差处理等功能。系统采用VC++软件编制出功能完善、操作简便、显示直观的标定系统上位机界面[7]，按照图5的流程图完成标定过程。

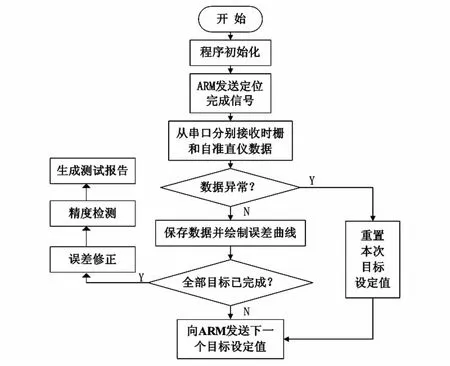
图5　上位机软件流程图Fig 5　Software flow chart of upper PC

当下位机ARM发送定位完毕信号后，上位机便开始 从串口分别读取时栅和自准直仪的数据信息，若此时读到的数据是正确的，则把上述的两个数据作差作为时栅传感器的原始误差保存到数据库，并在屏幕上显示误差曲线；若此时读到的数据不正确，则通知下位机重新定位这个目标点。判断所有的目标点是否定位完成，若没有完成，则向下位机发送下一个目标点的设定值；若所有目标点的数据都采集完成，则程序根据误差模型对时栅传感器的系统误差进行修正，并实现测试报告的自动生成，从而完成误差修正工作。

3.1步进电机的控制

步进电机的控制是数控系统的重要组成部分，时栅转台定位精度取决于电机控制的质量，因此，电机控制质量将会对转台标定的准确性产生影响。根据经典控制理论的介绍，步进电机有单向逼近和双向逼近两种控制方法[8，9]。虽然双向逼近相比于单向逼近具有定位速度快的优势，但双向逼近会带来回程误差，为了获取高精度的定位，系统以ARM为核心，采用二分法进行单向逼近完成对步进电机的控制。按图6的流程预先设置一个角度值N，ARM自动将角度值转换为步进电机的脉冲数，脉冲数控制步进电机转动N—1度，然后每次转动剩下1/2的读数来逼近预设值。

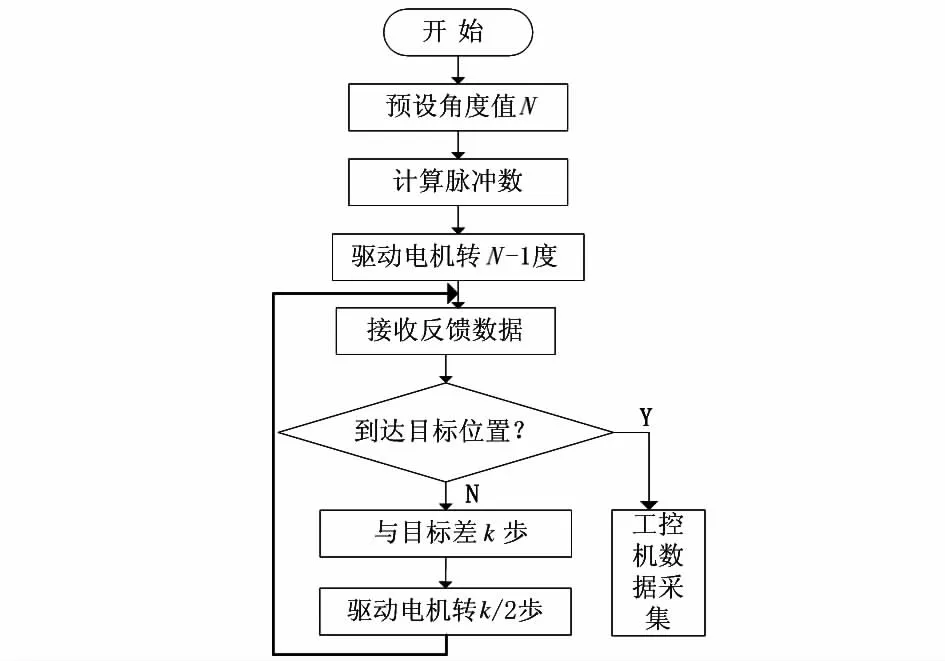
图6　电机单向逼近控制流程图Fig 6　Flow chart of one-way approximation motor contorl

3.2数据采集

数据采集按照图7的流程图进行。系统开机后，在上位机界面完成步进电机旋转方向和设备选择等参数的设置。变量初始化后开始测试，多面棱体随时栅转台同步匀速转动。当时栅转台转动到预定目标值时，自准直仪正对多面棱体面中心点。上位机程序发生中断事件，串口传送自准直仪和时栅的数据到上位机，数据保存后，重复此过程，直到转台整周23个数据点完成。

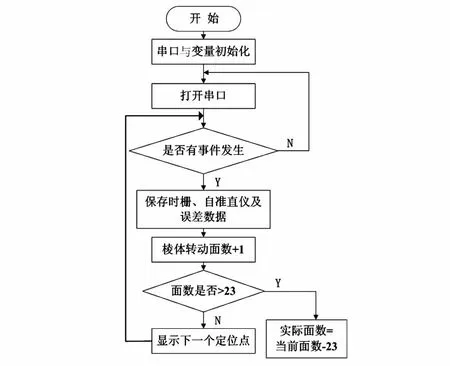
图7　数据采集流程图Fig 7　Flow chart of data acquisition

3.3谐波修正

谐波修正法是时栅传感器和先进检测技术中心依据时栅自身的结构特点所提出的一种方法，现已成功应用[6]。根据傅里叶级数的展开式可知，任何误差曲线都可以表示为含有1,2,3,...,N(N趋于无穷)次误差的函数，因此,在一个圆周上分布有m个读数头，那么就可以消去除km(k=1,2,3,…)次以外的各次误差。于是，在时栅旋转磁场内放置多个测头将时栅传感器测量误差进行分离,然后将采集到的误差值构成误差曲线，上位机对误差曲线进行分析并拟合出含有相同谐波次数的曲线，将误差曲线和拟合曲线作差来修正误差，重复多次对误差曲线拟合、修正，直到达到理想值。

本系统采用23面多面棱体是对装有72对极时栅的转台进行标定，将测得的时栅整周的23个误差数据来构成误差曲线，用含有主要谐波成分的拟合曲线对误差进行反复多次修正，直至误差曲线低于设计值。

4实验验证

为了验证本标定系统的可靠性，采用精度极高的九江公司生产的0级23面多面棱体和示值误差为±1″的自准直仪对装有72对极时栅的转台进行标定测试。实验装置如图8所示。

图8　系统装置Fig 8　System equipment

在转台转动的整周360°范围内每(360/23)°进行采点。采集整周后的原始误差和根据其谐波次数拟合出的曲线如图9所示，原始误差曲线和拟合曲线接近重合且主要含有一次谐波如图10，作差后得到图11所示的谐波修正后的误差曲线，一次谐波被消除，最终得到±1.3″的转台精度，达到设计要求。

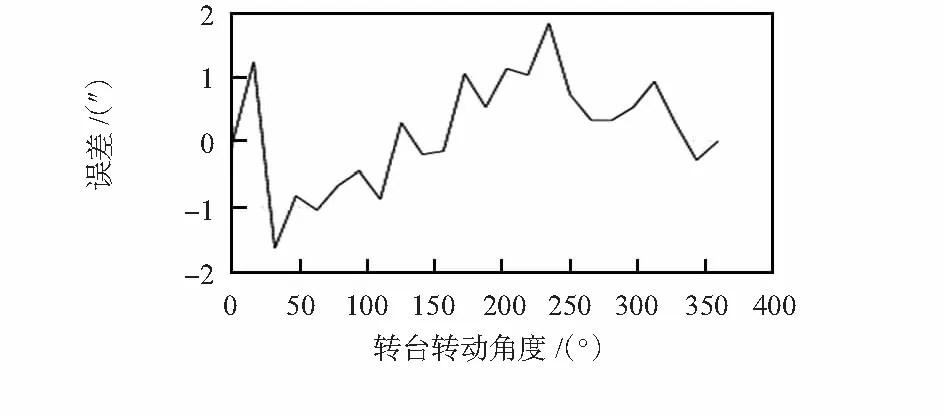
图9　整周实测误差曲线与拟合曲线Fig 9　Error curve of integer measurement and fitting curve

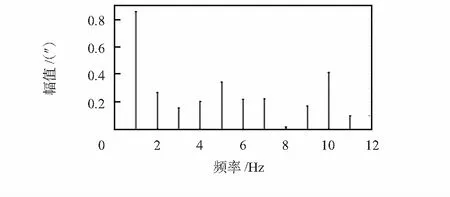
图10　傅里叶变换的幅值—频率曲线Fig 10　Amplitude-frequency curve of Fourier transform

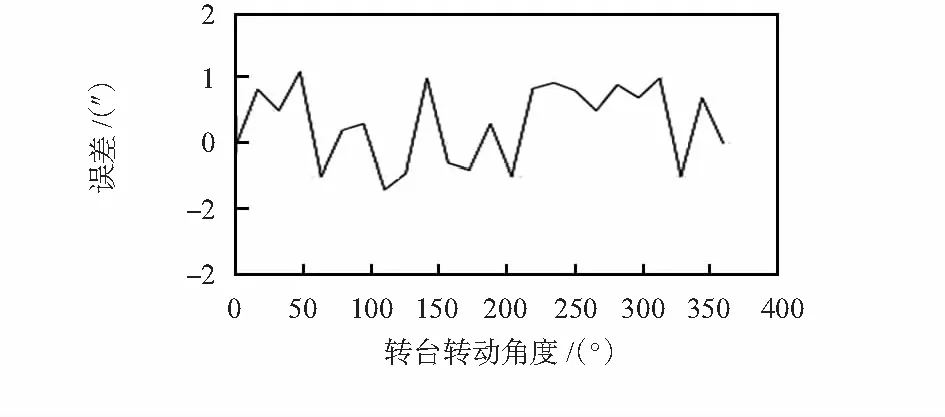
图11　谐波修正后的误差曲线Fig 11　Error curve after harmonic wave correction

5结束语

该系统以高精度的多面棱体和自准直仪为基准量对时栅转台进行标定，其中数控电机系统中的ARM对步进电机进行控制，不仅提高了标定的效率，而且减小了人为因素对测量结果的影响，提高了转台的定位精度。对于标定后的误差采用谐波修正方法进行多次修正，经实验证明:时栅转台的分度精度可以达到±1.3″，整个标定系统的设计可行。

参考文献:

[1]彭东林.时栅位移传感器与新型机床动态监测系统[M].北京：科学出版社，2010:56-86.

[2]PengDonglin，TanWeimin,LiuXiaokang,etal.Timespacecoordinatetransformationandtimegratingdisplacementsensor[C]∥ProceedingsoftheSecondInternationalSymposiumonInstrumentionScienceandTechnology,2002:440-444.

[3]刘小康,郑方燕.时栅数控转台空间回转位置预测方法研究[J].仪器仪表学报,2011,31(10):2303-2308.

[4]高同山.双轴电子自准直仪的应用之一测量多面棱体与角度块[J].中国计量，2008(9):77-79.

[5]林海波.单片机控制的步进电机斩波恒流细分驱动器的实现[J].电气传动与控制，2003(7):46-48.

[6]彭东林,刘小康,张兴红,等.基于谐波修正法的高精度时栅位移传感器[J].仪器仪表学报，2006,27(1):31-33.

[7]徐璇,姜明新,黄静,等.基于MFC的工程软件界面设计[J].电子设计工程，2011,21(19):11-13.

[8]陈锡侯,陈涛,彭涛,等.基于ARM和FPGA的三维精密定位控制系统[J].仪表技术与传感器,2011(5)：59-62.

[9]王安敏,牛传猛,崔伟.基于X-Y工作平台的步进电机闭环控制系统[J].微电机,2010,43 (1):103-105.

[10] 杨继森,何建，彭东林,等.基于STM32 的时栅转台高精度自动标定系统设计[J].传感器与微系统,2014,33(3):107-109.

[11]KulkarniAmol，El-SharkawiS，MohamedA.Intelligentprecisionpositioncontrolofelasticdrivesystems[J]．IEEETransactionsonEnergyConversion，2001，16(1):26-27.

Designofautomaticcalibrationsystemfortime-gratingturntablebasedonpolygons*

WANGShu-xian1，PENGDong-lin1,2，GAOZhong-hua1,2，ZHANGXu-yun1，ZHOUJin-gang1，ZHENGFang-yan1,2

(1.EngineeringResearchCenterofMechanicalTestingTechnologyandEquipment,MinistryofEducation,ChongqingUniversityofTechnology,Chongqing400054,China;2.KeyLaboratoryofChongqingCity,ChongqingUniversityofTechnology,Chongqing400054,China)

Abstract:Aiming at the problem of time-grating turntable precision reducing induced by sensor mounting eccentric or environmental changes and so on,present automatic calibration system for time-grating turntable which calibrates error by polygons and autocollinator and use harmonic wave correcting technology for error correction.Polygons and autocollinator high-precision measuring instruments are applied to the system as measuring standard,ARM processor is used as core to carry out closed-loop control on stepper motor and achieve precise positioning,and the system can carry out data acquisition and error processing.Experimental result shows that compared with manual mode,the calibration system is not only high efficient,but also indexing precision can reach ±1.3" after calibration.

Key words:polygons； autocollinator； time-grating displacement sensor; turntable; automatic calibration

DOI:10.13873/J.1000—9787(2016)04—0100—04

收稿日期：2015—07—13

*基金项目：国家自然科学基金资助项目(51127001)；国家重大科学仪器设备开发专项项目(2013YQ220893)；重庆理工大学研究生创新基金资助项目(YCX2014224)；重庆理工大学博士科研启动基金资助项目(2015ZD08)

中图分类号：TP 23

文献标识码：A

文章编号：1000—9787(2016)04—0100—04

作者简介:

王淑娴(1990-)，女，山东济宁人，硕士研究生，主要研究方向为智能检测与传感器技术方向的研究。