插入式电磁流量计的研究*
2016-06-24李小京
李小京, 路 璐
(天津工业大学 电气工程与自动化学院,天津 300387)
插入式电磁流量计的研究*
李小京, 路璐
(天津工业大学 电气工程与自动化学院,天津 300387)
摘要:研究提高插入式电磁流量计的准确度问题。通过改进流量计内部所插入线圈的物理结构与改进流量计的物理结构来提高测量精度。分别计算出传统流量计与改进后的流量计的磁通密度,并对流场进行数值耦合,获得电极两端的电动势,并与实验数值对比,误差分别为11.3 %,4.25 %,证明了所用方法的合理性。
关键词:电磁感应; 传感器; 插入式电磁流量计
0引言
插入式电磁流量计是在管道式电磁流量计的基础上发展起来的一种流体流量仪表,保留了电磁流量计测量原有的优点,克服了电磁流量计在大口径管道上安装困难、费用高等缺陷。
插入式电磁流量计主要由传感器和变送器组成。传感器将液体流量变换成感应电动势信号,并传输到转换器;转换器将传感器送来的流量信号进行放大,并将流量信号转换成电信号[1]。电极检测出的感应电势数值很小,通常是μV,因此,测量精度很容易受外界影响。
本文提出了通过向流量计内部插入铁芯和改进流量计的物理结构的方法,重新检测电极两端的电动势,并与实验数据相对比误差较小,比传统的插入式电磁流量计有着更好的精确度。
1插入式电磁流量计的基本方程
如图1所示,流体做切割磁感线运动所产生的感应电动势,通过电极引入到转换器中进行测量,以线圈匝数为2 620匝的传感器的物理模型为例,给出了插入式电磁流量
计的基本方程解。
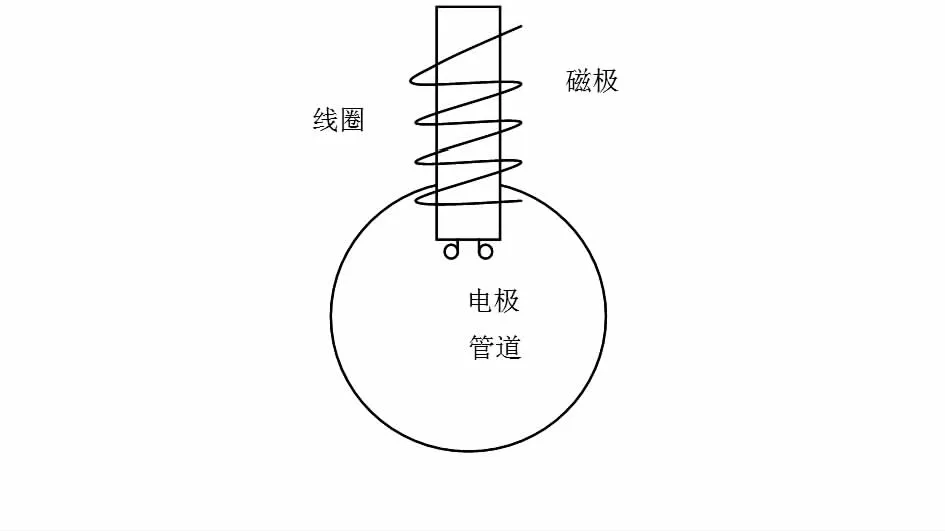
图1 插入式电磁流量计原理图Fig 1 Principle diagram of insertion electromagnetic flowmeter
已知插入式电磁流量计的基本方程为
UAB=2RBzvy=BDEv
(1)
如图2,当圆柱绕流为平面势流且磁场在z轴方向分布均匀时,磁场为定值Bz,流体流速为定值vy,两个电极间距为D,考虑有限区域影响时,两电极间的电位差通过辅助公式G(格林公式)可得[2]
(2)
由式(2)可知,当测量区域的边界固定,即h固定时,k为常数,且当h趋近于无穷大时,k值趋近于1。
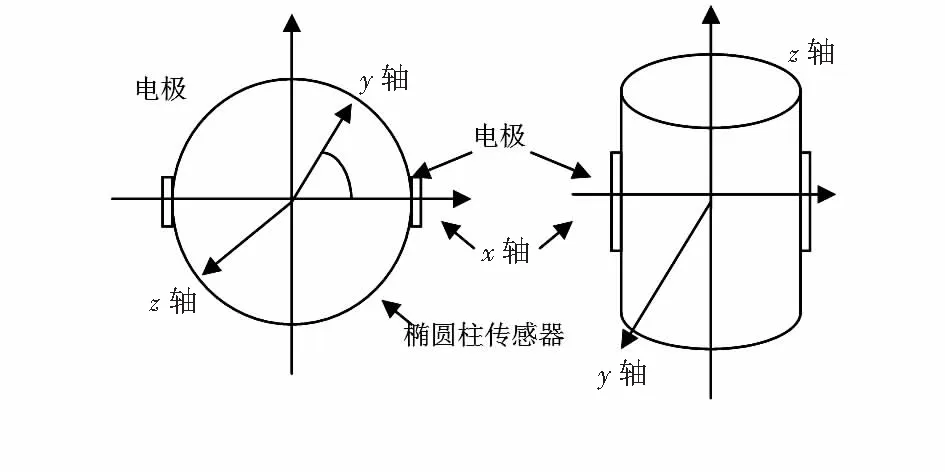
图2 椭圆柱型传感器的三维模型Fig 2 3D model for elliptic cylindrical sensor
2流量计电磁场的求解
当电流通过线圈时,会在线圈周围产生磁场。流量计测量杆的两侧各设置了一对电极,在流量计进行测量时,只需将电极置于管道的平均流速点上即可[3]。
本文采用MatlabPDE工具箱进行仿真,设置PDE参数,磁导率μ=1,电流密度:左边的线圈电流密度J=-1,右边的线圈电流密度J=1,其余传感器、管道、电极和铁芯区域电流密度均为0,传感器周围的电磁场如图3所示[2]。
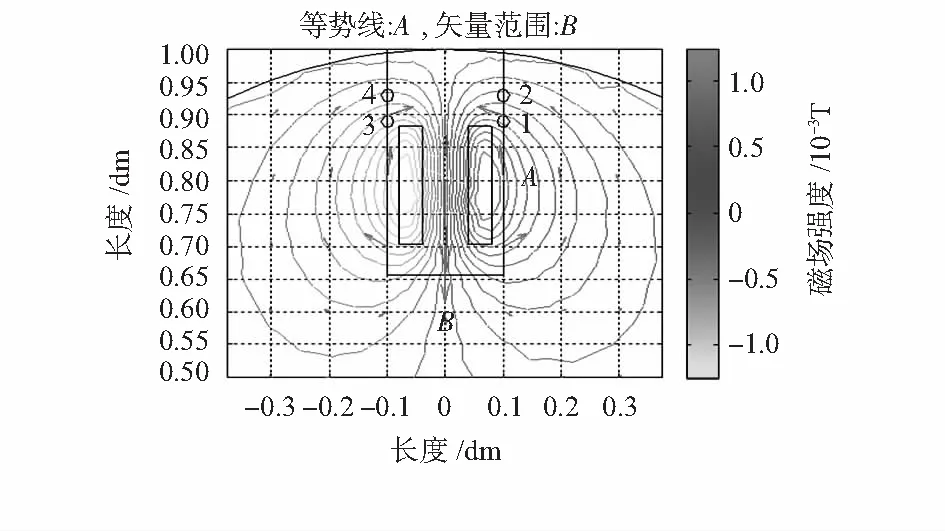
图3 传感器磁场仿真图Fig 3 Simulated diagram of magnetic field of sensor
如图3,传感器1,2对电极与3,4对电极连成的直线和磁场以及平均流速成相互垂直关系,由于电极所在位置的磁感应强度B较小,所以,液体流经电极时产生的感生电动势数值较小,容易受到外界的干扰[4]。
3改进的流量计电磁场求解
为了可以增加管道内的磁场强度,在线圈中插入“工”字型铁芯,并在测量杆的两侧安置新的电极[5]。铁芯二维模型如图4所示。
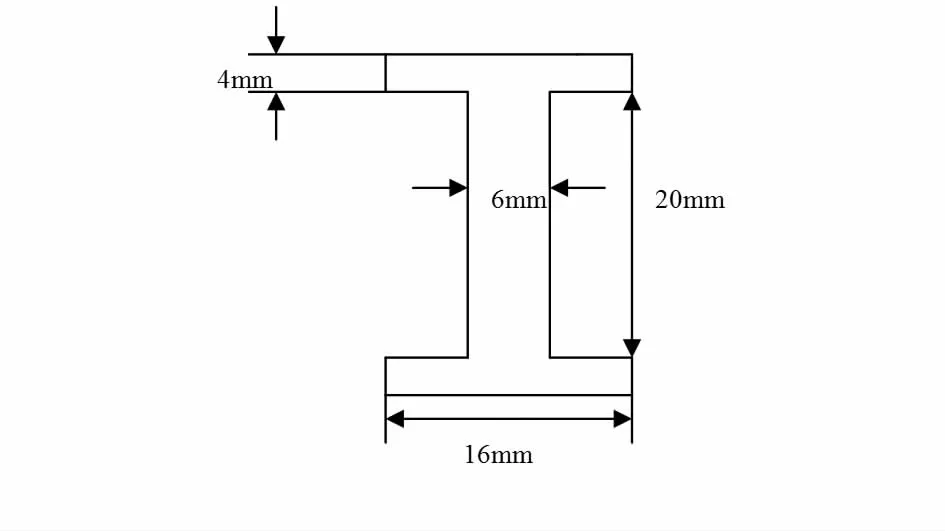
图4 铁芯模型Fig 4 Model for iron core
设置PDE参数,铁芯的磁导率μ=200,其余各个区域磁导率μ=1,左线圈中电流密度J=-1,右线圈中电流密度J=1,其余传感器、管道、电极和铁芯区域电流密度均为0。传感器周围的电磁场如图5所示。
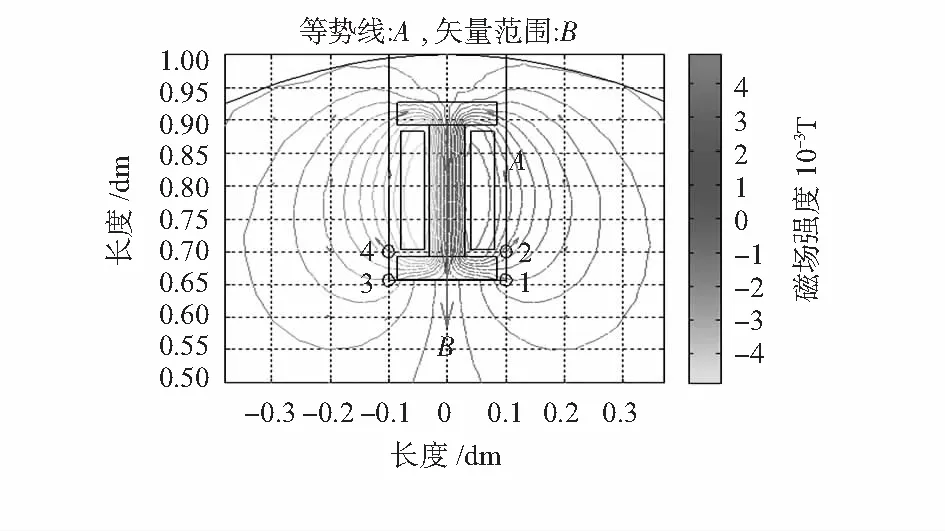
图5 传感器磁场仿真Fig 5 Magnetic field simulation of sensor
1,2对电极与3,4对电极连成的直线和磁场以及平均流速成相互垂直关系,液体流经电极时产生感生电动势。
表1中B1代表未插入铁芯的传感器电极所处位置的磁场强度,B2代表插入铁芯后电极所处位置的磁场强度。插入铁芯后,电极所在区域内的磁场强度明显增大,液体流经电极时产生的感生电动势数值较大,其抗干扰能力也得到了很大的提升[6,7]。
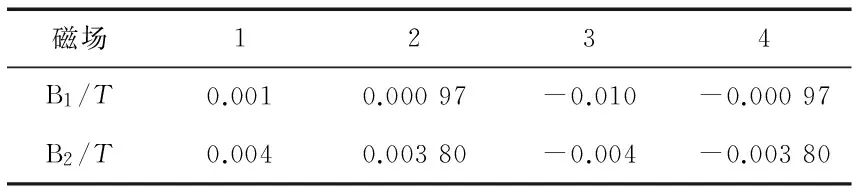
表1 磁场数据对比
4传感器的物理结构
传统的传感器为圆柱形,其几何图形如图6所示,管道直径0.2m,长1m,传感器为半径为0.02m的圆柱体[8]。
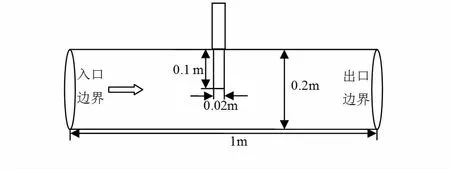
图6 传感器与管道模型图Fig 6 Model for sensor and pipeline
传感器的探入会使流体产生绕流现象,对流速的影响很大,降低了测量精度。雷诺数Re在绕流现象中起决定性作用,其公式如下[9]
Re=ρvL/μ
(3)
式中ρ,μ分别为流体密度和粘度,v,L分别为液体流场的特征速度和特征直径。本文所测量的流体为水,其粘度为μ=1.0×10-3Pa·s。随着Re的增大,圆柱背后的漩涡进一步扩大,并逐步周期性地脱落出旋转方向相反且排列规则的双列漩涡,经非线性作用后形成了著名的卡门涡街[10],导致两侧电极所检测到的流场产生严重的失真。
为了降低绕流物体的压差阻力,可以通过减小后部逆压梯度,将圆柱型传感器改造成椭圆柱型。
格子Bolzmann方法是一种计算流体力学的算法,将流体的宏观运动作为大量微观粒子运动的统计平均结果,宏观的物理量可由微观粒子的统计平均值得到。
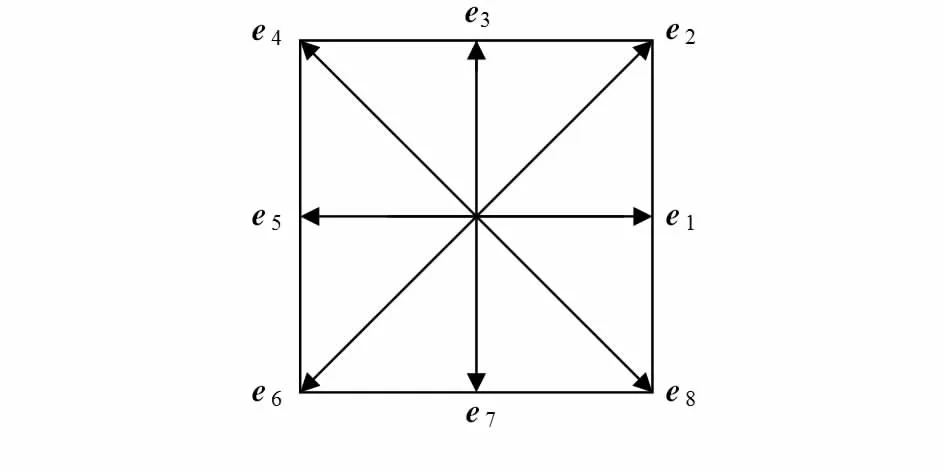
图7 二维速度模型Fig 7 2D model for velocity
α=1,2…7,8,fα(xb,t)为α方向上粒子速度分布函数。用动量转换法计算柱体受力,设eα是离散速度矢量,xf为流体节点,xb为固体节点,在α方向上,流体与柱体碰撞前的动量为eαfα(xf,t),碰撞后的动量为-eαfα(xb,t),动量改变量为-eα[fα(xb,t)+fα(xf,t)]。由力的相互作用可知,柱体受力为[9]
F=∑eα[fα(xb,t)+fα(xf,t)]
(4)
由此可得,阻力系数为
(5)
式中b为椭圆的竖直方向的半轴长,ρ为宏观量的密度,u为宏观量的速度
(6)
(7)
因此,在传感器所受外力不变的条件下,阻力系数与椭圆的半轴长b呈反比。流体经过传感器时所受阻力越小,流体流速所受传感器的影响越低。
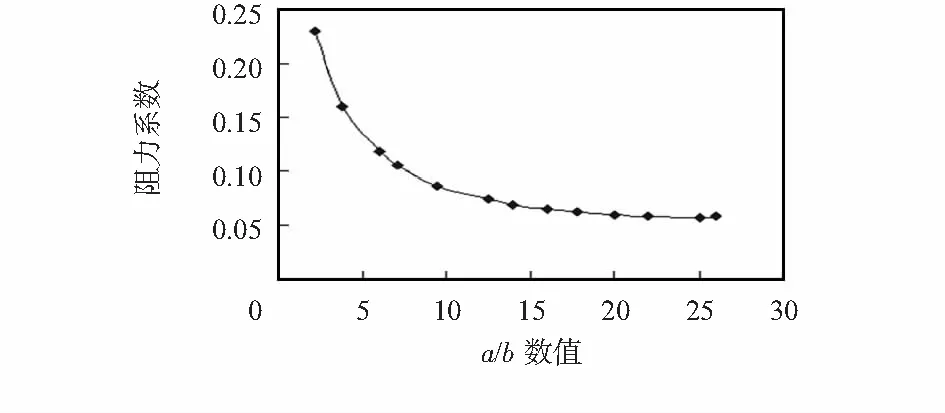
图8 阻力系数与a/b关系图Fig 8 Relationship between resistance coefficient and a/b
图8为阻力系数与椭圆柱的a/b比值变换关系,阻力系数随着a/b的增大而减小,液体绕流阻力减小,当a/b>25时,阻力系数增大[9]。由此可知,若保持a不变,将圆柱改为椭圆柱,即b增加,则a/b减小,阻力系数增加,此时阻力系数与Re数呈反比,因此,Re数减小,圆柱绕流程度降低。由此可知,将圆柱改为椭圆柱可以有效地降低绕流物体的压差阻力。本实验所使用的传感器为a/b=2的椭圆柱型。
本文利用Fluent软件分别对圆柱型传感器与椭圆柱型传感器周围的流场进行仿真,参数设置如表2所示。

表2 进口流速
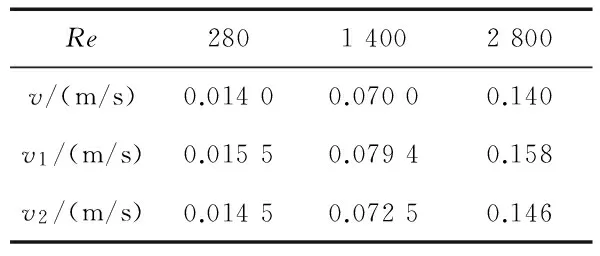
圆柱体与椭圆体形状的传感器流场速度矢量仿真如图9~图11,vc为圆柱体传感器所在管道的进口流速,ve为椭圆柱体传感器所在管道的进口流速。
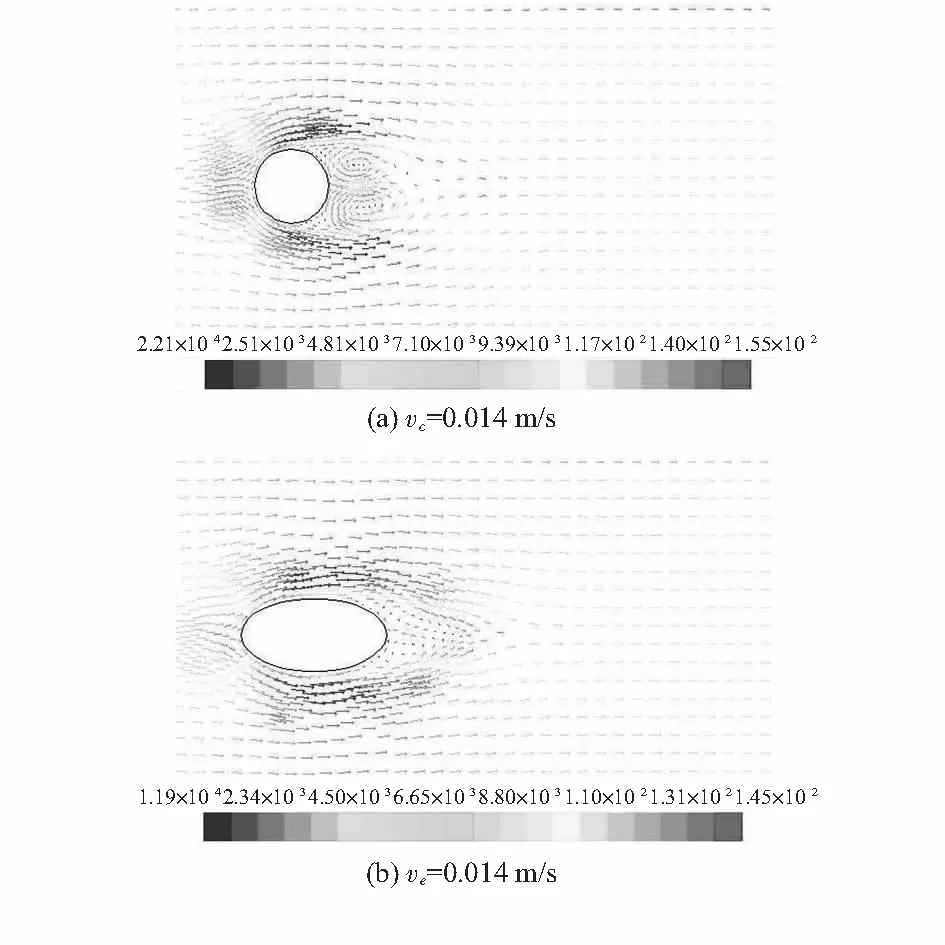
图9 Re=280速度矢量图(部分放大)Fig 9 Diagram of velocity vector while Re=280
仿真结果图中,当传感器为圆柱型时,随着Re的增大,圆柱背后的漩涡进一步扩大,并形成著名的卡门涡街,两侧电极所检测到的流场流速严重失真。
从表3可知,当传感器为椭圆柱体时,电极检测出的流速误差更小。这是因为其后部逆压梯度减小,绕流物体的压差阻力减小,从而降低了传感器两侧的电极受扰流的影响,提高了电极检测流速的精确度。
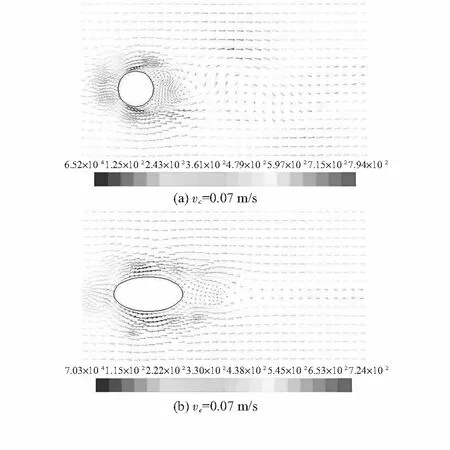
图10 Re=1 400 速度矢量图(部分放大)Fig 10 Diagram of velocity vector while Re=1 400
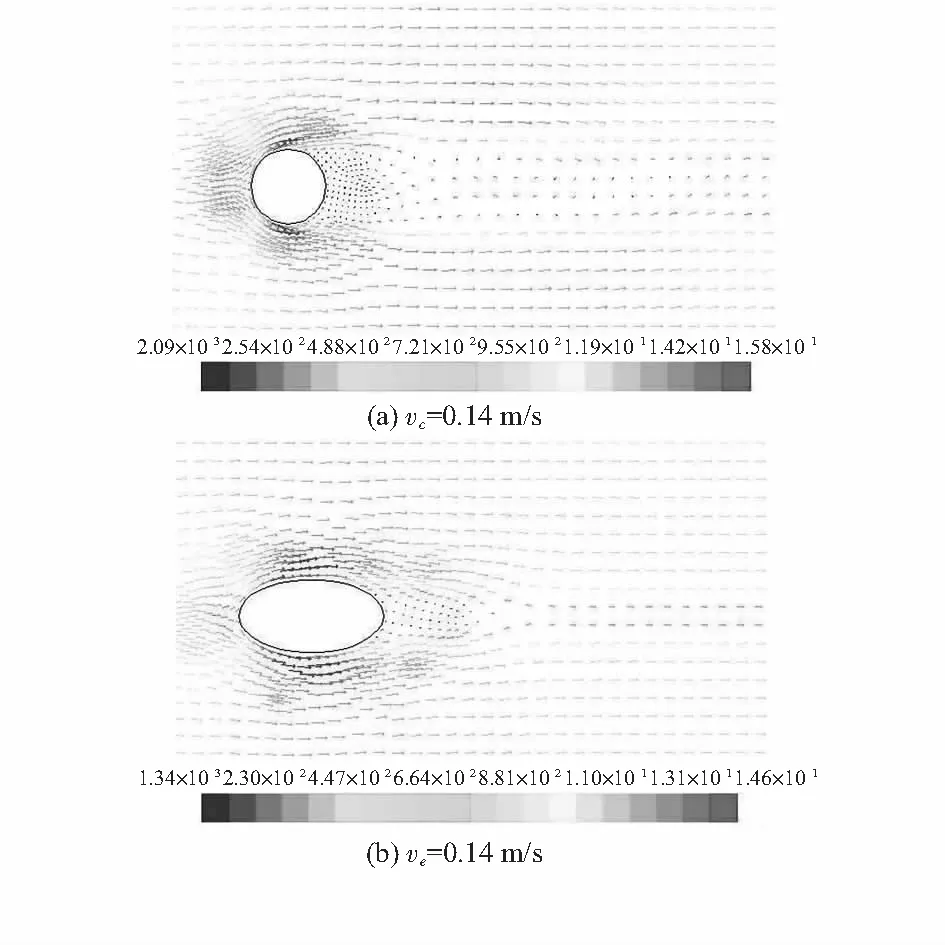
图11 Re=2 800 速度矢量图(部分放大)Fig 11 Diagram of velocity vector while Re=2 800
Re28014002800v/(m/s)0.01400.07000.140v1/(m/s)0.01550.07940.158v2/(m/s)0.01450.07250.146
5Fluent仿真与实验数据对比
Fluent软件分别对圆柱型和椭圆柱型传感器进行流场仿真,仿真数据与实验数据对比如图12所示。
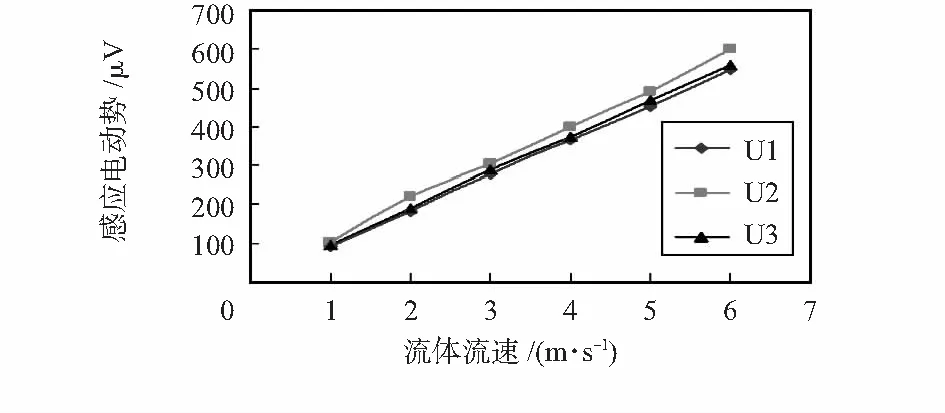
图12 仿真数据与实验数据对比图Fig 12 Simulaiton and experimental data contrast
U1,U2,U3分别为实测数据,圆柱型传感器仿真数据,椭圆柱型传感器仿真数据,从图中可看出:圆柱型传感器所测得感应电动势误差为11.3 %,椭圆形传感器所测得感应电动势误差为4.25 %。
6结束语
本文利用Matlab软件分别仿真出有无铁芯的流量计周围的磁场密度,通过增加磁通密度来提高流量计的抗干扰能力,增加电极所测到磁通B的精度。另一方面通过格子算法(Boltzmann)和动量转换计算出椭圆柱绕流的阻力,并利用Fluent软件最终仿真出椭圆柱体传感器四周的流场,与传统的圆柱体传感器相对比,发现椭圆柱体比圆柱体对流体所造成的绕流影响更小,其两侧电极所在位置的流速v的精确度更高。说明利用椭圆柱体代替圆柱体传感器有着更高的参考价值。
参考文献:
[1]赵宇洋,张涛,Lucas G,等.多电极电磁流量计转换器设计[J].传感器与微系统,2012,31(6):87-89.
[2]陈坚祯.一种新型多电极插入式电磁流量传感器及其基础研究[D].上海:上海大学,2009.
[3]袁加维,董连鹏.电磁流量计的分类和选型[J].农业与技术,2009,29(1):152-154.
[4]曹金亮.多参数电磁流量计及其实现技术的研究[D].上海:上海大学,2007.
[5]沈丹平.多电极插入式电磁流量计的研究[D].上海:上海大学,2009.
[6]杨勇.非满管电磁流量计测量方法与实验装置研究[D].合肥:合肥工业大学,2010.
[7]杨尚林,刘诗斌,郭博,等.铁芯参数对磁通门输入输出特性影响分析[J].传感技术学报,2014 (1):40-47.
[8]余行良,程留恩.一种新型电磁流量计传感器[J].自动化博览,2002,19(2):19-20.
[9]郑海成,施卫平,张合金,等.用格子Boltzmann方法计算椭圆柱绕流的阻力[J].吉林大学学报:理学版,2009,47(5):928-932.
[10] 闵强利.低雷诺数卡门涡街数值模拟[J].四川兵工学报,2009,30(11):81-83.
Studyoninsertionelectromagneticflowmeter*
LIXiao-jing,LULu
(SchoolofElectricalEngineeringandAutomation,TianjinPolytechnicUniversity,Tianjin300387,China)
Abstract:Research on improving methods for accuracy of insertion electromagnetic flowmeter.By improving physical structure of coil and improving physical structure of flowmeter to improve measuring precision of flowmeter.Respectively calculate magnetic flux density of traditional flowmeter and improved flowmeter,and numerical coupling of flow field is carried out,electromotive force at the ends of electrodes is obtained,and compared with experimental value,errors are 11.3 % and 4.25 %,respectively,rationality of the method is proved.
Key words:electromagnetic induction; sensor; insertion electromagnetic flowmeter
DOI:10.13873/J.1000—9787(2016)04—0038—04
收稿日期:2015—08—22
*基金项目:国家自然科学基金资助项目(61372011);天津市重点实验室项目
中图分类号:TB 937
文献标识码:A
文章编号:1000—9787(2016)04—0038—04
作者简介:
李小京(1955 -),男,山西太原人,硕士,教授,从事测量与控制、流量传感器设计与应用研究方向。
