基于马尔科夫模型下的水质评价

龙珂良,陈　星,崔广柏,林　松,王依依,范云柱

(河海大学水文水资源学院, 江苏 南京　210098)

基于马尔科夫模型下的水质评价

龙珂良,陈星,崔广柏,林松,王依依,范云柱

(河海大学水文水资源学院, 江苏 南京210098)

摘要：基于马尔科夫模型原理,对常熟市原型调水试验后水质改善情况进行动态评价。选定水质评价指标进行无量纲处理、隶属度划分、权重分配,构建概率转移矩阵,求出进步度,并对引水过程中污染物浓度的变化进行分析,从而进行水质评价。结果表明：调水试验后各断面水质均有相应变化,并且大部分断面水质在改善,离引水口最近的两个断面改善效果最为明显,部分断面因为引水不足以及沿程陆域污染等而导致水质有所恶化。

关键词：原型调水;马尔科夫模型;离差最大化赋权法;进步度

随着经济迅速发展,水污染已成为长江三角洲主要水环境问题,严重危害到人们的日常生活。大量含重金属的工业废水、生活污水、农业排水使得水质日益恶化,因此必须对水质进行改善,采用水质评价方法来判断水环境改善的效果。水质评价是指通过客观定量的方式描述水体状态,从而给水环境整治提供依据。水质评价方法多以静态评价为主,大多数未将污染物的时空分布与水质综合评价动态地进行结合。国内外常用水质评价方法有层次分析法[1]、相对差距和法[2]、主成分分析法[3]、TOPSIS法[4]、RSR值综合评价法[5]、人工神经网络法[6]和全概率评分法[7]等。实际上,江河湖库连通的过程中,污染物浓度的变化是一个随机的过程,具有很大的不确定性,因此一般的水质预测模型很难考虑这些随机因素,但是基于马尔科夫过程构建的马尔科夫模型是一种无后效性的随机过程,时间和状态都是离散的,可通过构建转移矩阵,确定水质变化进步度,进行水质评价。马尔科夫模型有数学基础作为支撑,具有其他评价方法不具有的优势,是目前国内外研究的热点。

常熟市位于长江三角洲经济发达区域,东北濒临长江,位于太湖流域下游的平原水网区,地势较低,河网分布密集,其经济发展与水环境之间存在矛盾。笔者选取常熟市常浒河以东、白茆塘以北地区为研究对象,在传统污染源治理的基础上,加强水系连通,加快水体流动,增加水环境容量,促进水环境改善。基于马尔科夫模型，对常熟市原型调水试验后水质情况进行动态评价,克服了一般水质模型的缺点,将各项污染物评价指标的时空分布与水质综合评价动态结合[8]。

1研究方法介绍

数学家马尔科夫根据切比雪夫在概率论中的研究,进行了独立随机变量和古典极值理论的研究,改进并完善了概率论中的中心极限定理及大数定律。马尔科夫对随机变量序列进行了深入研究,得到了马尔科夫随机过程,即“马尔科夫过程”。在此基础上,马尔科夫链和马尔科夫模型应运而生。随着“马尔科夫过程”的提出,它已经成为现代概率论与数理统计中随机过程分支理论的一个重要组成部分。

1.1马尔科夫模型原理

已知一个系统或一个转换过程处于t时刻的状态,当它处于t+1时刻的状态只与t时刻的状态有关,而与t时刻之前的所有状态都无关。这种性质被称为无后效性[9]。

将上述性质用概率分布函数来表示,假设随机过程t时刻系统所处的状态为xn,t+1时刻所处的状态为xn+1,则t+1时刻系统所处状态xn+1下的条件概率可表示为

(1)

其中,pij为马尔科夫链的一步转移概率。

相应的,由pij(h)组成一个矩阵成为h步转移矩阵:

(2)

特别地,当h=1时,此时称为一步转移矩阵。

(3)

1.2进步度

a. 划分质量状态。常见的水质划分是将原始数据直接分类,大约有3～6个状态,但是这种方法会导致大量数据集中在一个类别中,区别度不大,达不到划分水质的目的。因此,要重新规划隶属度更精细的划分标准,将上述每个指标、每个状态无量纲规范化的数据进行划分,一般划分为11个状态,如下表1。

表1　马尔科夫无量纲规格化后的水质状态划分

b. 进步度。其实,一步转移矩阵已经能够大致判断水质的变化情况,但是为了避免马尔科夫概率矩阵发生多步转移,在求得一步转移矩阵后进行进步度求解,这样能更直观、更精确地判断水质改善情况。求解进步度公式如下:

(4)

式中:i,j=1,2,…,11,进步度矩阵S(i,j)=sij。当进步度为正数时,表示水质得到了改善;当进步度为负值时,表示水质得到了恶化。进步度的绝对值越大,表示水质改善(或恶化)的程度越大。pk=∑sij为第k个断面的进步度,根据pk来动态评价常熟市水循环调控后各断面水质改善情况。

2实例应用

2.1马尔科夫模型计算

常熟市原型调水监测时间为12:00～24:00,引水期徐六泾、金泾最大引水流量分别达55.1 m3/s和43.3 m3/s,平均流量分别为31 m3/s和24.2 m3/s。沿程各河道由于所处位置和河道规模的差异,分流情况差别较大,在引水期间,盐铁塘断面水流运移速度缓慢,汇入常浒河和白茆塘,而东环河由于离排水河道近,受到监测前河道排水的影响,引水期河道仍然处于排水阶段,且流量很大,东环河平均流量为20.5 m3/s。选取常熟市常浒河以东、白茆塘以北地区为研究区,该区位于常熟市的滨江地带,地势比较低洼,河网分布密集,具有代表性。对区内7个水质监测断面进行马尔科夫模型求解,选取TP、TN、NH3-N、CODMn4个指标作为评价指标体系,动态地对各断面进行对比评价。研究区各断面具体位置见图1。通过对各个断面引水后水质的变化情况来评价该区在原型调水试验后的水质情况。

图1　研究区各断面具体位置

根据指标无量纲化处理和质量划分状态,这4个指标都属于越小越优型,求出各断面的隶属度矩阵(由于篇幅问题,下面仅列出两个断面计算过程)如下:

得到隶属度矩阵后,由VB编写程序,通过最大化离差权重分析法公式,得到各指标权重。指标权重为ω1=(0.411,0.227,0.738,0.485);ω2=(0.134,0.648,0.376,0.648)。

各断面初始矩阵如下:

统计隶属度矩阵中相邻两次监测值由i级变到j级的个数,从而求得概率转移矩阵为

由概率转移矩阵,根据式(4)求得进步度矩阵为

2.2结果分析

2.2.1进步度分析

由上述进步度矩阵可以求出相应断面的进步度:s1=0.36;s2=-0.39;s3=0.22;s4=-0.06;s5=0.08;s6=0.89;s7=1.89。

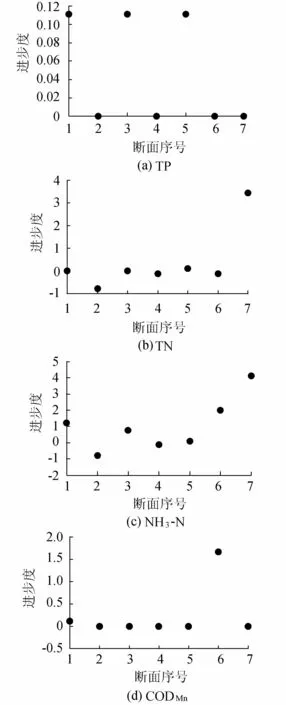
s2

a. 断面7,6,1,3,5水质都有所改善,而断面2,4水质相对有所恶化,断面7,6,1,3,5改善程度依次呈递减趋势。

b. 由于断面2引水阶段流向改变为盐铁塘至徐六泾时,各项水质指标浓度普遍呈上升趋势,而且断面2水质浓度较断面1上升很大,这是因为引水的中途盐铁塘水流携大量污染物质汇入徐六泾断面2。断面4与2情况一致,引水的中途盐铁塘水流携大量污染物质汇入金泾断面4。

c. 断面6、7距离徐六泾、金泾入河处比较近,所以引水对其水质状况改善比较大,而断面1、3相对较远,且要途经里睦塘,因此这两个断面相对于断面6、7水质改善较小。断面5位于清水港上，距离引水口比较远,所以水质改善不明显。

d. 徐六泾断面6到断面1、金泾断面7到断面3水质改善程度明显下降,主要是因为徐六泾、金泾沿程工厂较多,周边水质较差小水系汇入这两条河流。同时由于断面6到1沿程距离要比断面7到3沿程距离要短,因而断面1相比断面3水质改善明显。

7个断面水质指标监测数值直接反映此次调水对常熟市水质的改善状况。调水期间各水质指标(TP 、TN、CODMn、NH3-N)质量进步度曲线随断面变化如图2所示。

图2　各污染物指标不同断面下质量进步度变化

分析图2可得到以下结论:

a. 在调水过程中,常浒河以东、白茆塘以北地区各断面各污染物指标浓度的进步度总体呈现正值,表明污染物指标浓度随着调水过程的持续、水体连通性的改善,总体趋势是下降的,因此,江河湖连通调水过程对研究区各断面污染物指标质量的改善效果显著。

b. 进步度特征明显不同的是TP和CODMn,由图2可见,两者的进步度在水质改善最好的断面7处反而减小,分析其原因,主要是受调水日天气影响,导致河底底泥扰动剧烈,致使该断面TP和CODMn浓度增大,水质变差,但后期TP和CODMn进步度为正,表明改善水体连通性的调水过程对降低调水区河流TP和CODMn浓度的效果还是显著的。

c. 在实际引水过程中,徐六泾比金泾引水流量略大一点,但是断面7相比断面6水质改善更明显,主要原因是建新塘位于徐六泾引水口位置很近,引水期间分流作用明显;并且徐六泾区域内河道本底水质较差,因而断面6相比7水质改善差。徐六泾断面2、金泾断面4、清水港断面5在调水不同阶段均存在时段流量减小、水质指标浓度增大现象。表明现有方案引排流量不足以改善区域水环境,引水流量有待加大、引水时段尚需加长。

2.2.2污染物浓度分析

调水期各断面污染物质量浓度变化过程线如下图3所示。

根据图3可以得出以下规律:

a. 在调水期间,各断面污染物指标浓度随调水流量和时间的变化总体呈现下降趋势。断面2、3、4污染物指标浓度呈现锯齿形波动,变化相对不明显,主要是由于离引水口距离较远。

b. 各断面污染物指标浓度基本随着调水流量的增加而减小,到了后期,随着调水流量的减少而略微回升。

c. 调水河流断面离调水路线的源头起点越远,断面污染物指标浓度变化越小,表明该断面水环境综合质量改善程度越差。

3结论

a. 通过马尔科夫模型计算转移矩阵,从而得出进步度,对水质进行动态评价。事实证明,通过马尔科夫模型计算出来的结果与评价得出的结论和实际情况一致,具有一定的科学性。马尔科夫模型在水质评价方面引入了状态的概念,给定了状态空间,从而得出水质变化的趋势,但是在指标权重的计算精度方面仍需要考虑,并加以改进。

图3　调水期间各断面污染物质量浓度变化过程线

b. 在常熟市原型调水试验过程中,常浒河以东、白茆塘以北地区各条河流断面污染物指标浓度的进步度绝大部分为正,表明本次调水试验对改善常浒河以东、白茆塘以北地区河流水质效果显著。总体而言,在调水试验过程中,在江河湖连通性改善的情况下,断面水环境综合质量虽然小幅度震荡性变化,但总体呈现上升趋势,表明随着调水过程的进行、调水水量的增加、水体连通性的改善,各断面水环境综合质量有一定程度的改善。

c. 马尔科夫模型的状态矩阵随机性较强,应综合应用其他水质模型,将其结果与该模型结果进行对比分析,从而更好地预测水质变化。

参考文献：

[ 1 ] 邓雪, 李家铭, 曾浩健, 等. 层次分析法权重计算方法分析及其应用研究[J]. 数学的实践与认识, 2012, 42(7): 93-99. (DENG Xue, LI Jiaming, ZENG Haojian, et al. The weights calculation method and application of analytic hierarchy process [J]. Mathematics in Practice and Theory, 2012, 42 (7): 93-99. (in Chinese))

[ 2 ] 王晖, 陈丽, 陈垦, 等. 多指标综合评价方法及权重系数的选择[J]. 广东药学院学报, 2007, 23(5): 583-589. (WANG Hui, CHEN Li, CHEN Ken, et al. Choose for multiple index comprehensive evaluation method and weighting coefficients [J]. Journal of Guangdong College of Pharmacy, 2007, 23(5):583-589. (in Chinese))

[ 3 ] 何成刚. 马尔科夫模型预测方法的研究及其应用[D]. 合肥: 安徽大学, 2011:7-13.

[ 4 ] 张又, 刘凌, 姚秀岚, 等. 引江济太调水中望虞河水质变化的规律[J]. 水资源保护, 2013, 29(2): 52-57. (ZHANG You, LIU Ling, YAO Xiulan, et al. Variation of water quality of Wangyu River during water diversion from Yangtze River to Taihu Lake [J]. Water Resources Protection, 2013, 29(2):52-57. (in Chinese))

[ 5 ] 李学法, 王守峰, 李超, 等. 基于马尔科夫模型的区域水环境安全评价[J]. 安徽农业科学, 2012, 40(28): 13903-13906. (LI Xuefa, WANG Shoufeng, LI Chao, et al. Water environment assessment based on Markov model [J]. Journal of Anhui Agricultural Sciences, 2012, 40(28):13903-13906. (in Chinese))

[ 6 ] 陈华友.多属性决策中基于离差最大化的组合赋权方法[J].系统工程与电子技术,2004,26(2):194-197. (CHEN Huayou. Combination determining weights method for multiple attribute decision making based on maximizing deviations [J]. Journal of Systems Engineering and Electronics, 2004, 26(2):194-197. (in Chinese))

[ 7 ] 马惠群,刘凌,陈涛.改进的多指标水质动态评价模型及应用[J].武汉大学学报:工学版,2008,41(5):54-57. (MA Huiqun, LIU Ling, CHEN Tao. Improved dynamic evaluation model of multifactorial water quality and its application [J]. Engineering Journal of Wuhan University, 2008, 41(5):54-57. (in Chinese))

[ 8 ] 周鹏飞.湖泊健康综合评价指标体系研究[J].安徽农业科学,2012,40(21):11005-11007. (ZHOU Pengfei. Research on the synthesis apprisal index system of lake heath [J]. Journal of Anhui Agricultural Sciences, 2012,40(21):11005-11007. (in Chinese))

[ 9 ] 郭金玉,张忠彬,孙庆云.层次分析法的研究与应用[J].中国安全科学学报,2008,18(5):148-153. (GUO Jinyu, ZHANG Zhongbin, SUN Qingyun. Research and application of analytic hierarchy process(AHP) [J]. Journal of Safety Science and Technology, 2008, 18 (5):148-153. (in Chinese))

[10] 覃春乔, 陈星, 张其成, 等. 基于马尔科夫模型的污染物质量浓度变化规律[J]. 水资源保护, 2014, 30(3): 56-60. (QIN Chunqiao, CHEN Xing, ZHANG Qicheng, et al. The pollutant concentration variation based on Markov model [J]. Water Resources Protection, 2014,30 (3): 56-60. (in Chinese))

Water quality evaluation based on Markov model

LONG Keliang, CHEN Xing, CUI Guangbo, LIN Song, WANG Yiyi, FAN Yunzhu

(CollegeofHydrologyandWaterResources,HohaiUniversity,Nanjing210098,China)

Abstract：Based on the principles of the Markov model dynamic evaluation was conducted to investigate the improvement of water quality after an experiment on prototype water diversion in Changshu City. Tthe water quality evaluation indices were selected for the dimensionless analysis, the division of the degree of membership, and the allocation of weights. The probability transfer matrix was established to obtain the degree of progress, and the change of concentrations of pollutants in the process of water diversion was analyzed, in order to evaluate the water quality. The results show that the water quality of all the sections have changed after the water diversion. The water quality of most of the sections improved, with the most significant improvement seen in the two sections nearest the water inlet. Meanwhile, the water quality of some sections deteriorated due to insufficient water diversion and pollution in the land area along the water diversion route.

Key words：prototype water diversion; Markov model; method of maximizing deviations to weighting; progress degree

DOI：10.3880/j.issn.1004-6933.2016.02.027

基金项目:江苏省科技支撑计划(BE2011697)

作者简介:龙珂良(1992—),女,硕士研究生,研究方向为水文物理规律模拟及水文预报。E-mail: 309811672@qq.com 通信作者:陈星,讲师。E-mail: Chenxing@hhu.edu.cn

中图分类号：X522;X132

文献标志码：A

文章编号：1004-6933(2016)02-0133-06

(收稿日期：2015-12-28编辑：徐娟)