OPGW 架空输电系统任一点接地短路电流分布的研究

齐 郑，饶 志，杨琳琳

(1.华北电力大学电气与电子工程学院，北京 102206；2.国网北京市电力公司，北京 100031)

OPGW 架空输电系统任一点接地短路电流分布的研究

齐 郑1，饶 志1，杨琳琳2

(1.华北电力大学电气与电子工程学院，北京 102206；2.国网北京市电力公司，北京 100031)

架空输电线路发生接地短路时，短路电流在光纤复合架空地线(OPGW)上的分布对电力系统有重要影响。传统计算 OPGW 线上短路电流的方法大多采用工程简化计算和基于序分量法的计算，并且只考虑接地短路发生在杆塔处的情形，计算结果过于粗糙。为此提出了基于相分量模型对全线任一点接地短路电流计算的方法。分别提出接地短路发生在杆塔处和杆塔间不同的数学模型，进一步求解相导线和OPGW每一级档距上的电流。数值算例验证了在杆塔处接地短路分流模型的正确性，杆塔处接地短路的分流结果进一步验证了杆塔间接地短路分流模型的正确性，并在实际工程中进行了应用。对于复杂的OPGW架空输电系统，基于相分量模型的计算方法能够准确计算全线任一点发生接地短路时，OPGW 线上短路电流的分布情况。

光纤复合架空地线；架空输电线路；杆塔；任一点接地；短路电流分布

0 引言

光纤复合架空地线(OPGW)具有传统架空地线防雷和分流的功能，同时兼具光纤通信的作用，在架空输电线路上的应用越来越普遍[1-3]。因此，OPGW线的选型和校验显得非常重要。热校验便是其中一个重要指标，定量计算出发生接地短路时，OPGW线 上 电 流 大 小 便 是 其 中 的 关 键[4]。 我 国 大 部 分110 kV 及以上的交、直流输电线路均采用双架空地线配置，目前的趋势是采用 OPGW 线来取代普通架空地线。OPGW 线运行方式的改进对减小线上的电能损耗效果明显，但这些技术手段也无法避免地造成了线路运行状况更加复杂[5]。

通过广泛的调研发现，简化算法、基于序分量的方法和基于相分量的方法是目前计算 OPGW 线上短路电流的三类主要方法[6-8]。简化算法忽略的重要因素太多，导致计算结果粗糙。序分量法计算的一个重要前提是系统三相参数对称，但实际线路运行状况复杂，对称的条件很难满足，导致计算结果仍然过于保守。基于相分量的计算方法则能充分反应输电线路的复杂运行状况。国外 Dawalibi博士在理论和实践方面做了大量的工作[9-10]，国内文献对相分量法计算架空地线上短路电流分布已经开展了较有成效的研究[11-16]，但注意到都只是对接地短路发生在杆塔处的情形进行了分析，对故障发生在杆塔之间的模型没有讨论。本文采用网孔法对 OPGW架空输电线任一点接地短路进行分析，包括接地短路发生在杆塔处和杆塔间的情况，形成一套完整的计算体系，同时用数值实例对短路电流的量化计算进行了验证。

需要说明的是，接地短路包括单相接地短路和两相接地短路，文中分别建立了这两种情形下的数学模型。

1 架空输电系统任一点接地短路电流计算

架空输电线路的 OPGW 线和三相载流导线共同组成一个空间平行多导体系统，形成输电线路的统一电磁场。各平行导体的相互位置、电荷情况、接线方式等，都会直接影响该电磁场的分布，进而决定 OPGW 线上感应电量的大小。在实际线路中，由于每条 OPGW 线与三相载流导线的空间位置并不对称，在 OPGW 上便会有电磁感应分量。基于相分量模型的计算考虑了相线和 OPGW 线之间的互感影响，各导线间的互感计算参考文献[17]中的相关公式。如图1 所示，以 5D1-SJ3 塔型为例，线间距离可以通过计算塔型中双回线路与 OPGW 之间的距离确定，高电压等级下相线采用的是多分裂导线，通常情况下，取相线等效中心到 OPGW 的距离作为计算各导线之间互感抗的原始参数。

线路运行时，由于积污等原因造成绝缘子闪络，此时可作为接地短路发生在杆塔处来处理；不可忽略的是，在杆塔间的部分由于人为或自然因素导致的接地短路也时有发生。由于两种情况均有各自的特殊性，数学模型也不相同。

OPGW架空输电系统运行模型如图2所示。

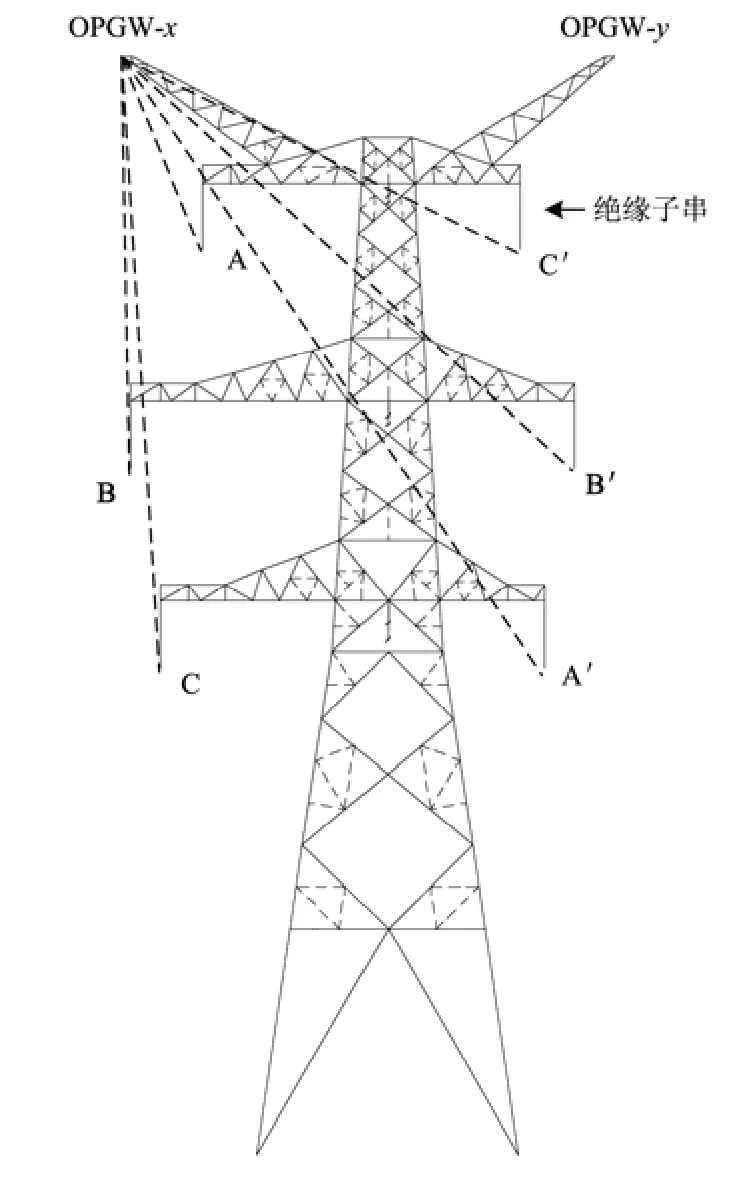
图1 线间距离计算示意图Fig. 1 Diagram of distance calculation between wires

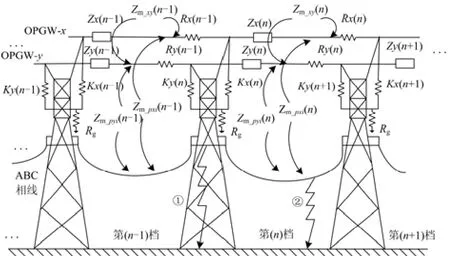
图2 输电线路运行示意图Fig. 2 Diagram of transmission system operation

图2 中 OPGW-x 和 OPGW-y 构成架空输电线路的双地线系统，以杆塔为自然分段节点，形成各级档距，以第 n 档为例，对其中的参数进行说明：Zx(n)表示第 n 档内 OPGW-x 的自阻抗，Zy(n)表示第 n 档内 OPGW-y 的自阻抗；Zm-pxi(n)表示第 n 档内输电导线的第 i相对 OPGW-x 的互阻抗，Zm-pyi(n)表示第 n档内输电导线的第 i相对 OPGW-y 的互阻抗(其中 i分别表示 A、B 和 C 相)；Zm-xy(n)表示第 n 档内OPGW-x 和 OPGW-y 之间的互阻抗；Rx(n)和 Ry(n)分别表示第 n 档内模拟 OPGW-x 和 OPGW-y 分段绝缘运行的开关电阻：开关电阻闭合则说明无分段绝缘运行，开关电阻断开则说明分段绝缘运行，这种设置能够有效地表现出 OPGW 在水平方向上的电气连接状况；Kx(n)和 Ky(n)分别表示第 n 档内模拟OPGW-x 和 OPGW-y 在杆塔处是否接地运行的开关电阻：开关电阻闭合则说明在该级杆塔处接地运行，开关电阻断开则说明在该级塔处非接地运行，这种设置能够有效地表现出 OPGW 在垂直方向上的电气连接状况；Rg表示每级杆塔的等效接地电阻。图2中①表示接地短路发生在杆塔处，②表示接地短路发生在杆塔之间。

1.1 杆塔处接地短路

本文讨论的是双端电源输电线路。将图2转换成如图3所示的等效电路图。接地短路包括单相接地短路和两相接地短路，本文在 ABC 三相线的短路点引入了一个“接地黑箱”。对于单相接地短路(本文以 A 相为例)和两相接地短路(本文以 AB 两相为例)，接地黑箱的含义分别如图4(a)和图4(b)所示，其中 Idk表示故障点的短路电流，Zdk表示故障点的接地阻抗。图4(a)表示短路发生在杆塔处的情形，短路电流 Idk一部分先经过 Zdk，再经杆塔入地，一部分通过 OPGW 返回；图4(b)表示短路发生在杆塔间的情形，短路电流 Idk直接经 Zdk入地，电流分布的量化值与短路类型、短路点的位置有重要关系。

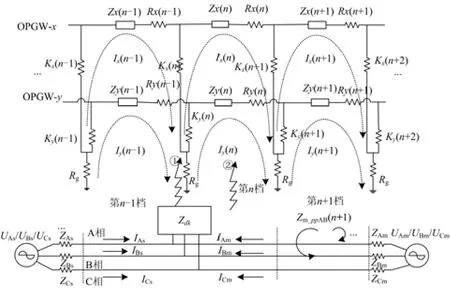
图3 杆塔处接地短路等效电路图Fig. 3 Equivalent circuit diagram of grounding fault at tower

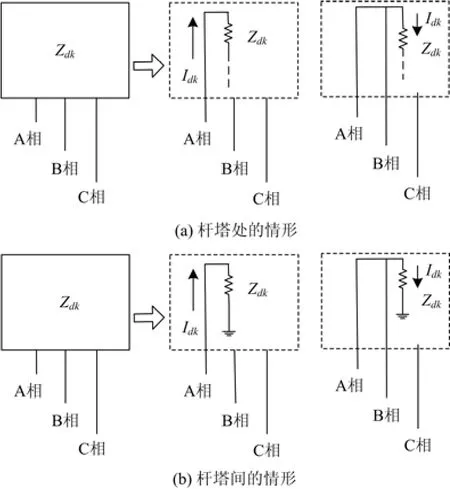
图4 接地黑箱两种情形下的示意图Fig. 4 Black-box of grounding faults

从线路首端到短路点，导线的相分量方程如下(从短路点到线路末端方程类似)：

以第n-1级档距和第n级档距之间的杆塔为例：A 相接地短路时的方程如式(1)所示，其中 i表示讨论 OPGW 对相线感应电压时的档距编号，则从线路首端到短路点之间的档距可依次编号为 i=1,2,3,…, n-2,n-1。由于每档 OPGW 上的电流、OPGW 和 A相之间的互阻抗都不同，造成每档两条 OPGW 对 A相的感应电压不同。因此从 i=1 到 i=n-1，将 OPGW对 A 相的感应电压求和，即得到式(1)中总的感应电压表达式。

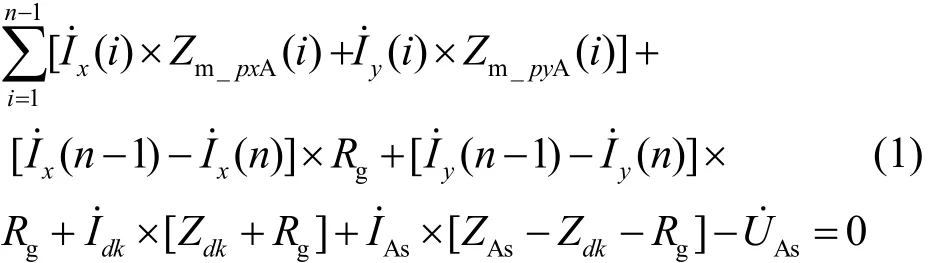
式(2)和式(3)表示 AB 两相接地短路时的方程。需要说明的是，式(1)—式(3)中参数 i含义相同；式(2)和式(3)中参数 j表示讨论相线间感应电压时的档距编号，j是为了与 i有所区别，两者并无实质不同。

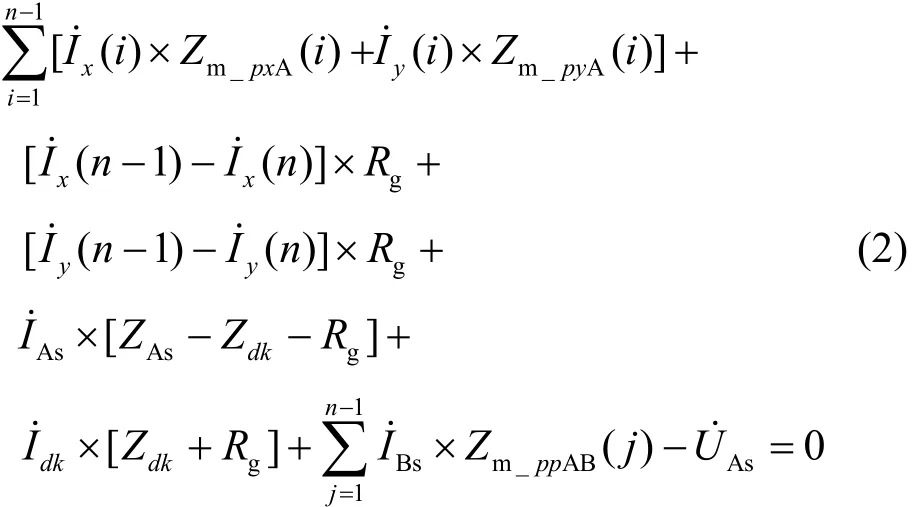
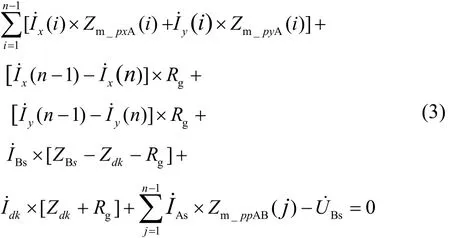
式(2)和式(3)中 Idk如式(4)所示。

注意到，和短路点有直接联系的网孔，在列写方程时要重点考虑对短路电流源的处理。为了不增加网孔的数目，图5将短路电流源等效变换为电压源处理。本文重点列出第 n-1 和第 n 档的回路电压方程，其他和短路电流无直接联系的网孔可去掉 Idk的相关项，列写较为简单，不再赘述。

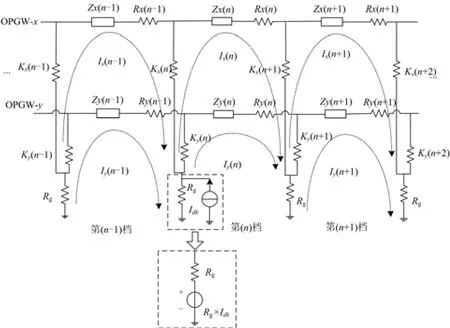
图5 杆塔处接地短路简化图Fig. 5 Simplified circuit diagram of grounding fault at tower

分别列出 OPGW-x和 OPGW-y第 n-1 级档距所满足的方程，如式(5)和式(6)所示。

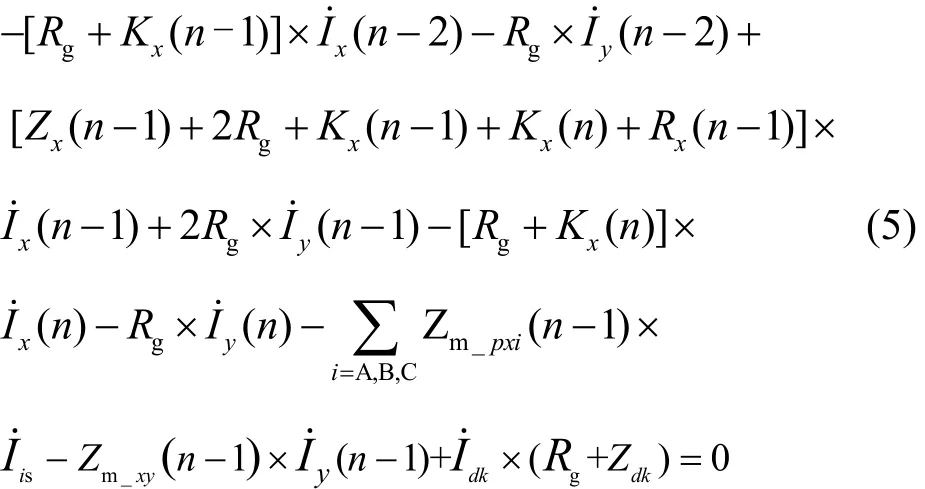
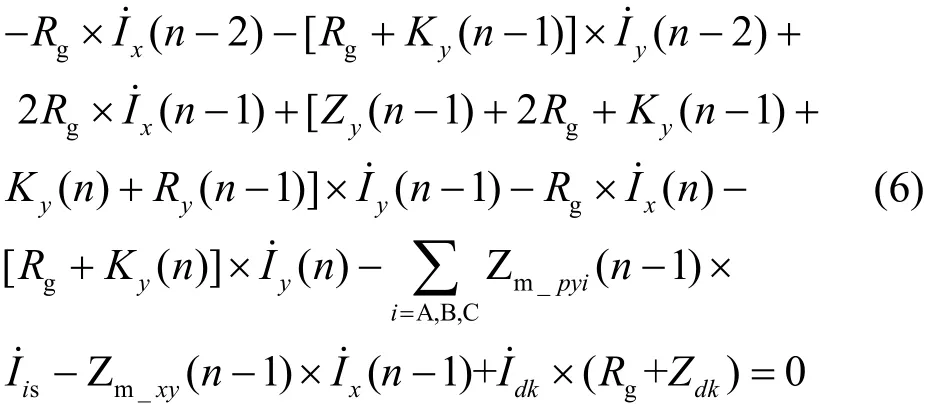
分别列出 OPGW-x 和 OPGW-y 第 n 级档距所满足的方程，如式(7)和式(8)所示。

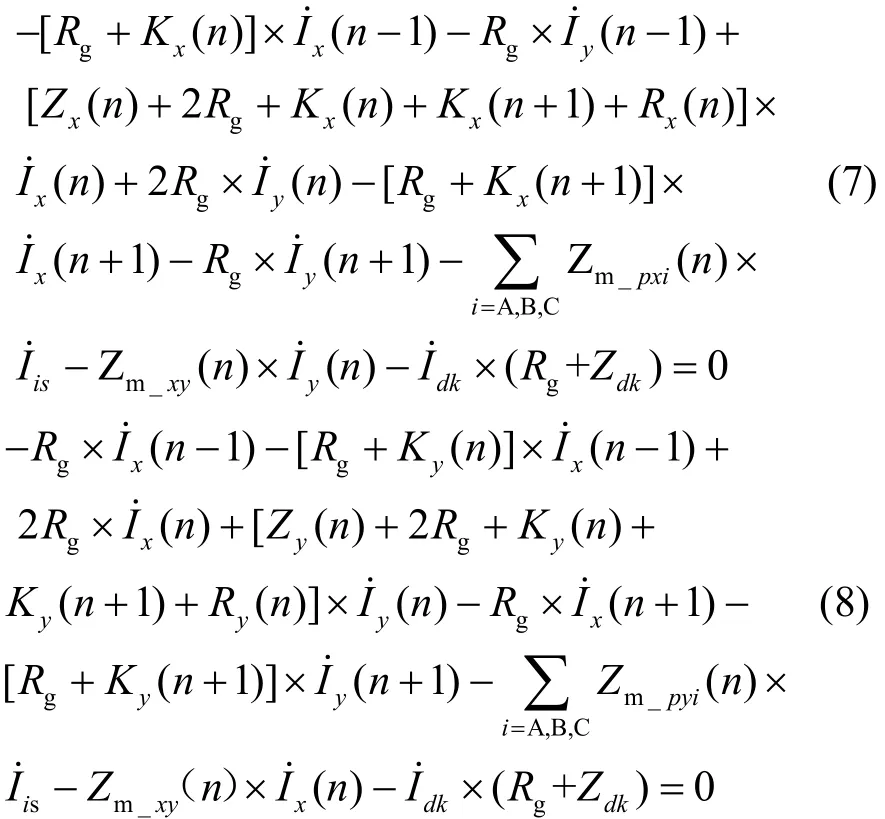
本节讨论的是接地短路发生在杆塔处的情形，通过文中的计算模型，列写出两条 OPGW 和三相导线之间满足的所有相分量方程，形成电网络求解，即可得到图5 中每档内 OPGW-x和 OPGW-y 上的电流，并且在计算机程序的帮助下，计算过程很容易完成。以该回路电流值为分析基础，接地短路发生在杆塔处时，OPGW输电系统一系列相关电气量就能进行求解。

1.2 杆塔间接地短路

线路运行中，在两杆塔间发生接地短路的模型如图6所示，该模型中的所有的参数和图5中的对应相同，是图2和图3中②的情形。根据短路后电磁环境和实际电阻率的综合考虑，确定短路电流的三条分流路径[18-20]。文献[19]是本课题组成员的前期研究成果，本文在其基础上对该模型进行了更深入的研究。用等效电阻值来模拟分流路径，随着在两塔之间的短路距离的变化，分流支路上的短路电流也在变化的。根据实际工程的处理经验和现场运行的数据，本文的处理方法是用 Rf1和 Rf3来表示接地点到两侧杆塔的地电阻，等效从地面流过并上杆塔的路径。此时，杆塔处是极端的条件，一侧路径的等效电阻最大，相对应的另一侧路径的等效电阻最小；设定 Rf1和 Rf3之和为定值，并且随着短路点从前一级杆塔到后一级杆塔的位置变化而变化；用Rf2来等效直接入地的路径，虽然大地电阻率等因素变化，但在此分流路径上仍可用一个定值表示，用参数 λ表示该值的大小。同时短路电流 Idk从这三个并联电阻 Rf1，Rf3和 Rf2的节点注入。为了减少回路数，将短路电流 Idk和 Rf2进行了如图7 的变换，图中 If1和 If2分别表示在杆塔间短路下，新增的两个回路中的网孔电流。

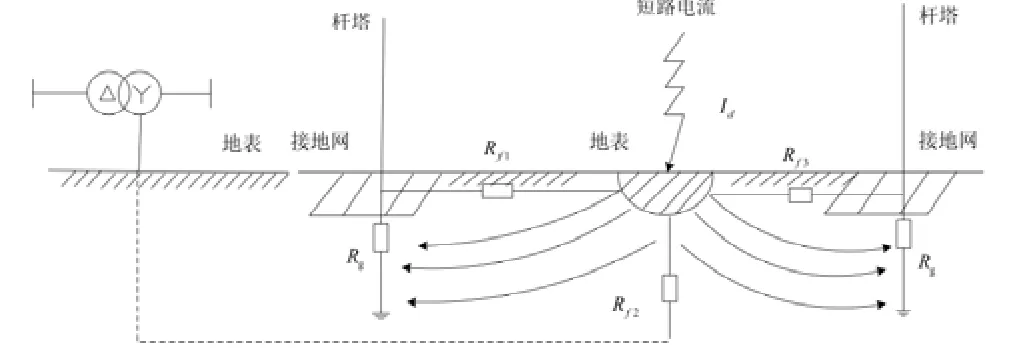
图6 短路电流分流路径等效示意图Fig. 6 Diagram of fault current distribution

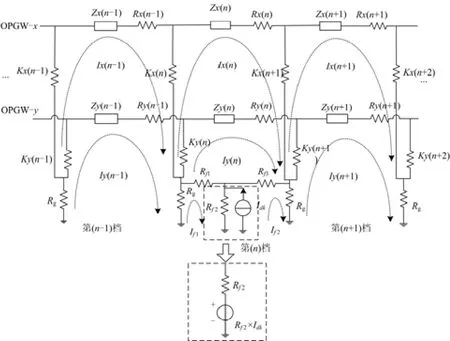
图7 杆塔间接地短路简化图Fig. 7 Simplified circuit diagram of grounding fault between towers

电阻 Rf1，Rf3和 Rf2的表达式分别如式(9)、式(10)和式(11)所示。在下式中，a(k)表示第 k 级档距的长度；Lf表示短路点到线路始端的距离；ρ 表示大地电阻率；参数 α，β，λ表示根据输电线路的实际运行环境决定的一系列系数，用来表征等效电阻值的大小。需要说明的是，由于在两杆塔之间发生短路的情形，工程中实际采集到的数据匮乏，但以上等效拟合的电阻值可以通过对线路实际运行环境综合得到，模型的可靠性将在下一节中进行验证说明。

从线路首端到短路点，导线的相分量方程如下(从短路点到线路末端方程类似)。

以第 n 档内发生单相接地短路为例，式(12)表示A相的方程：

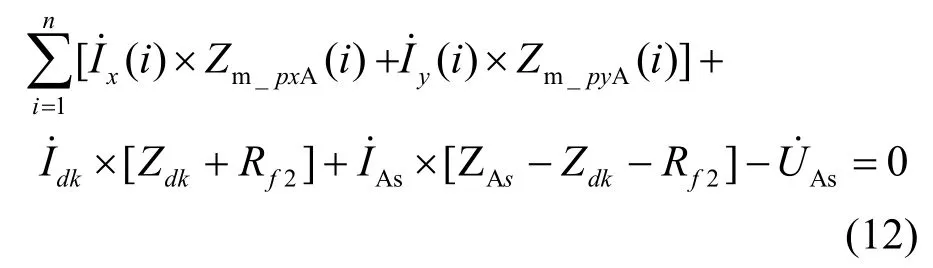
以第 n 档内两相接地短路为例，式(13)和式(14)表示AB相的方程。

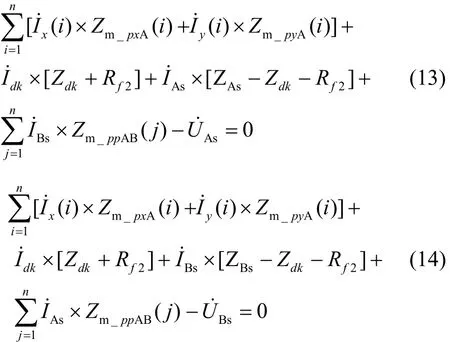
式(12)—式(14)与式(1)—式(3)中参数 i 含义相同；式(13)、式(14)与式(2)、式(3)中参数 j含义相同。

分别列出 OPGW-x和 OPGW-y 第 n-1 档内所满足的方程，如式(15)和式(16)所示。

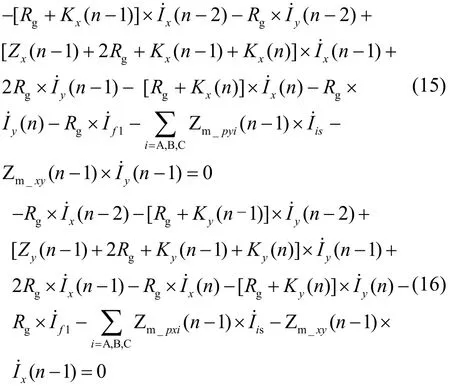
分别列出 OPGW-x 和 OPGW-y 第 n 级档距内所满足的方程，如式(17)和式(18)所示。

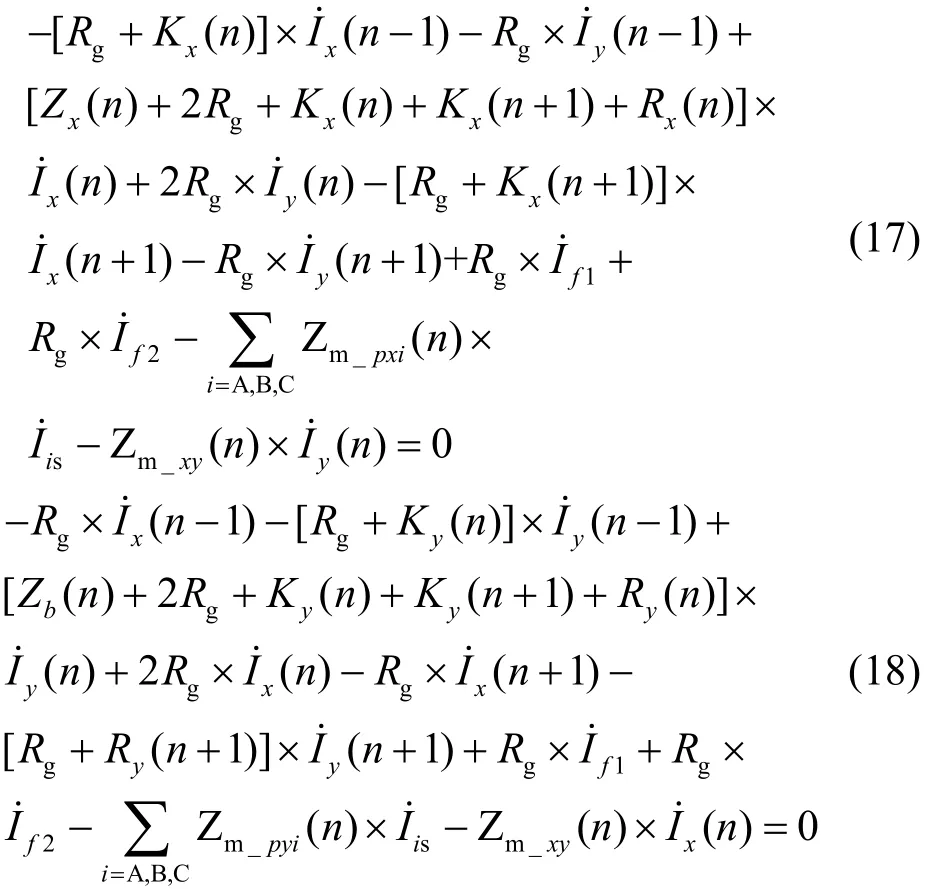
分别列出 OPGW-x 和 OPGW-y 第 n+1 级档距内所满足的方程，如式(19)和式(20)所示。

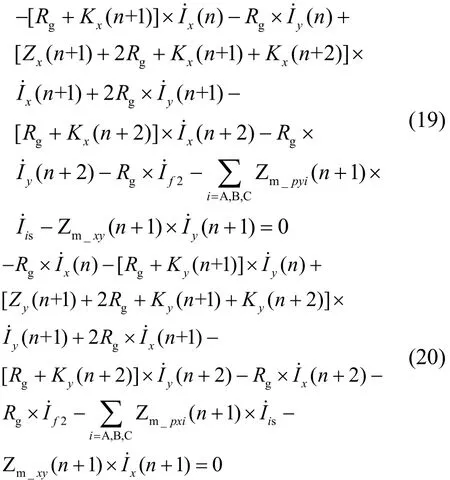
式(21)和式(22)表示图6 中两个增广接地网孔满足的方程：

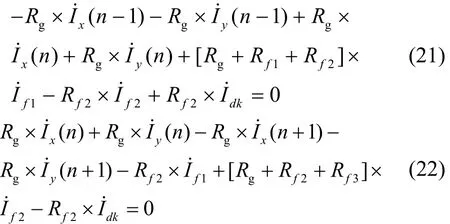
本节讨论的重点是接地短路发生在杆塔间的情形，计算过程和杆塔上的情形相似，模型的建立和方程的正确列写是正确计算的保障。本文综合考虑大地电阻率等影响因素，将此时的分流路径进行等效，选取合适的相关参数，建立电网络，便能对一系列的电气量进行求解。

2 算例验证与应用

在架空输电系统的工程实际中，发生接地短路时，OPGW 线上的短路电流数据，没有装置对其进行过监测。通过广泛的文献调研发现，文献[9]的作者作为相分量模型计算接地系统短路电流的奠基人，其论文算例作为验证后续改进方法正确性的准则，在文献[11]、文献[13]以及文献[14]等论文中均采用此方法进行验证。

在这节中分两方面来进行说明：一方面采用文献[9]中的算例与本文的计算结果进行比较；另一方面采用文献[9]中的算例，通过杆塔处接地短路的计算结果来验证杆塔间接地短路计算的结果。

2.1 杆塔处接地短路验证

文献[9]中以一条两端供电的单地线输电线路为例，线路长 100 km，每档距长度平均为 0.5 km，共 200 级档距，杆塔等值接地电阻 Rg=0.01 kΩ，在线路中部发生单相接地短路。与本文的计算结果比较如表1所示。

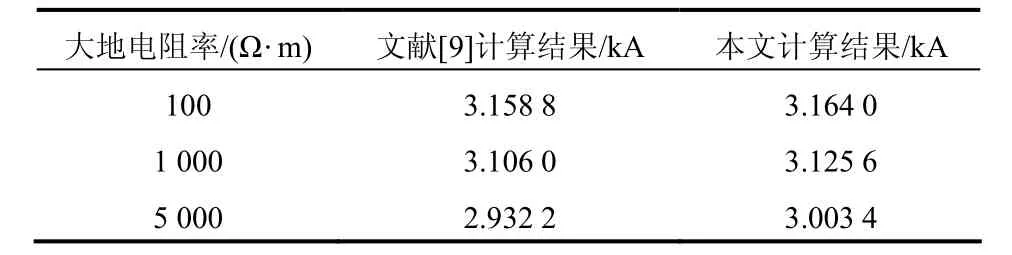
表1 短路电流计算结果比较表一Table 1 Result comparison table 1

如果该条线路只有左侧的电源供电，右侧视为负荷，和本文的计算结果比较如表2所示。

表2 短路电流计算结果比较表二Table 2 Result comparison table 2

从表1和表2中我们可以看到，对于地电阻率从100 mW × 到5000 mW × 变化的过程中，本文的计算结果和文献[9]中的结果匹配较好，从而能够验证本文计算方法的正确。

2.2 杆塔间接地短路验证

如前文所述，包括文献[9]在内的文献都是以接地短路发生在杆塔处展开讨论的，本文通过杆塔处的计算结果对杆塔间的情形进行验证。仍采用文献[9]中的算例，进行如下的计算：以逐级杆塔发生单相接地短路；以档距值的二分之一为短路步长进行单相接地短路。大地电阻率取1000 mW× ，在两种不同的情形下，整条线路 OPGW 线上短路电流分布如图8所示。

为更清晰地分析，将图8局部放大后如图9所示。

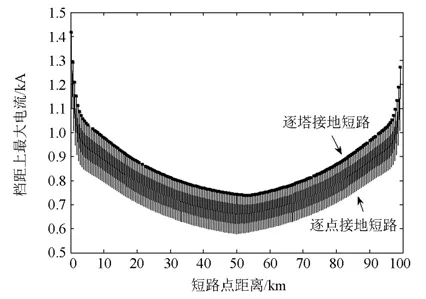
图8 杆塔间接地短路验证图Fig. 8 Verification diagram of grounding fault between towers

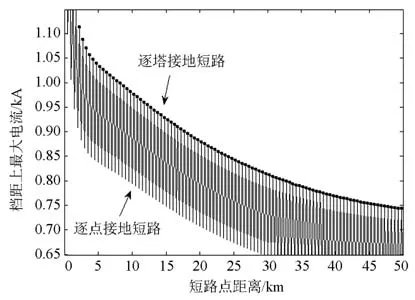
图9 局部放大图Fig. 9 Diagram of partial magnifying

如图9中标记点所示，全线在逐塔发生接地短路和全线逐点短路计算的极大值点重合，形成包络的形式，短路步长取在两杆塔之间，此时接地短路，OPGW 线分流作用不明显，处于全线逐点短路计算的极小值点。两种不同模型下，杆塔处短路时的计算结果一致，从而验证了在杆塔间短路计算的正确性，从而说明两者能够形成统一的计算体系。

2.3 实际线路应用

基于以上理论开发的计算软件已投入到实际工程应用中，能够方便计算出架空输电系统任一点发生接地短路时，相导线和 OPGW 线上短路电流分布情况。下面以某 500 kV 高压输电线路为例，该工程参数如下：采用同塔双回配置；导线型号采用JL/LHA1-400 铝合金芯铝绞线，导线为 4 分裂，分裂间距为 450 mm(正方形边长)，双 OPGW 线组合，计算塔形主要采用 5D1-SZ2；线路全长 120 km，共240 级杆塔，每档的平均档距为 0.5 km；两侧变电站内等效接地电阻为 0.5 Ω，每级杆塔的接地电阻取10 Ω，土壤电阻率1000 mW× 。双回路从首端变电站出线时，左右两侧的相线分别如图10所示的ABC和 CBA 排列，全线经三次换位，换位塔分别为 N52、N126、N280 号塔，具体换位方式见图11。

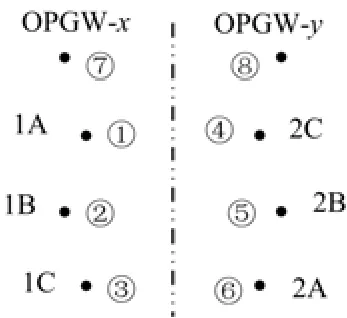
图10 导线分布示意图Fig. 10 Diagram of wires distribution

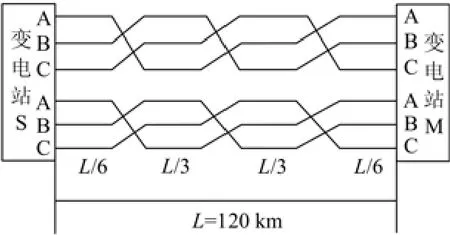
图11 导线换位示意图Fig. 11 Diagram of wire transposition

通过计算，短路电流分布如图12 所示，具体数值见表3。在双端电源线路中，随着故障杆塔向线路末端推进，首端电源提供的短路电流逐渐减小，末端短路电流逐渐增大，若两侧系统参数相差不大，则短路电流分布曲线近似对称。

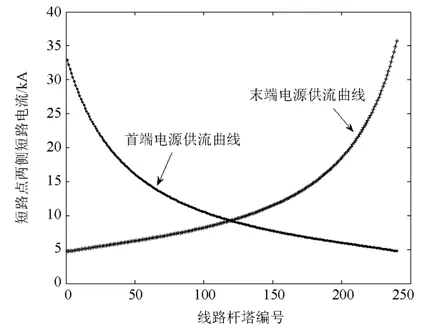
图12 短路电流分布示意图Fig. 12 Diagram of fault current distribution

通过计算，每一级杆塔发生单相接地短路的短路后，故障杆塔前两档和后一档中两条 OPGW 线上短路电流见表4。

每次在杆塔处发生接地短路，故障杆塔的邻近档内，OPGW 线上短路电流值最大。从表4中的数值可以看出，随着故障杆塔向线路末端推进，OPGW短路电流最大位置逐步由故障杆塔的前一档变成了故障杆塔的后一档。表4中的数据能够清楚看出在线路任意级杆塔处短路时，OPGW 线上短路电流分布情况；当然，本计算系统对于杆塔间的任一点的接地短路情况也能很好地进行求解。

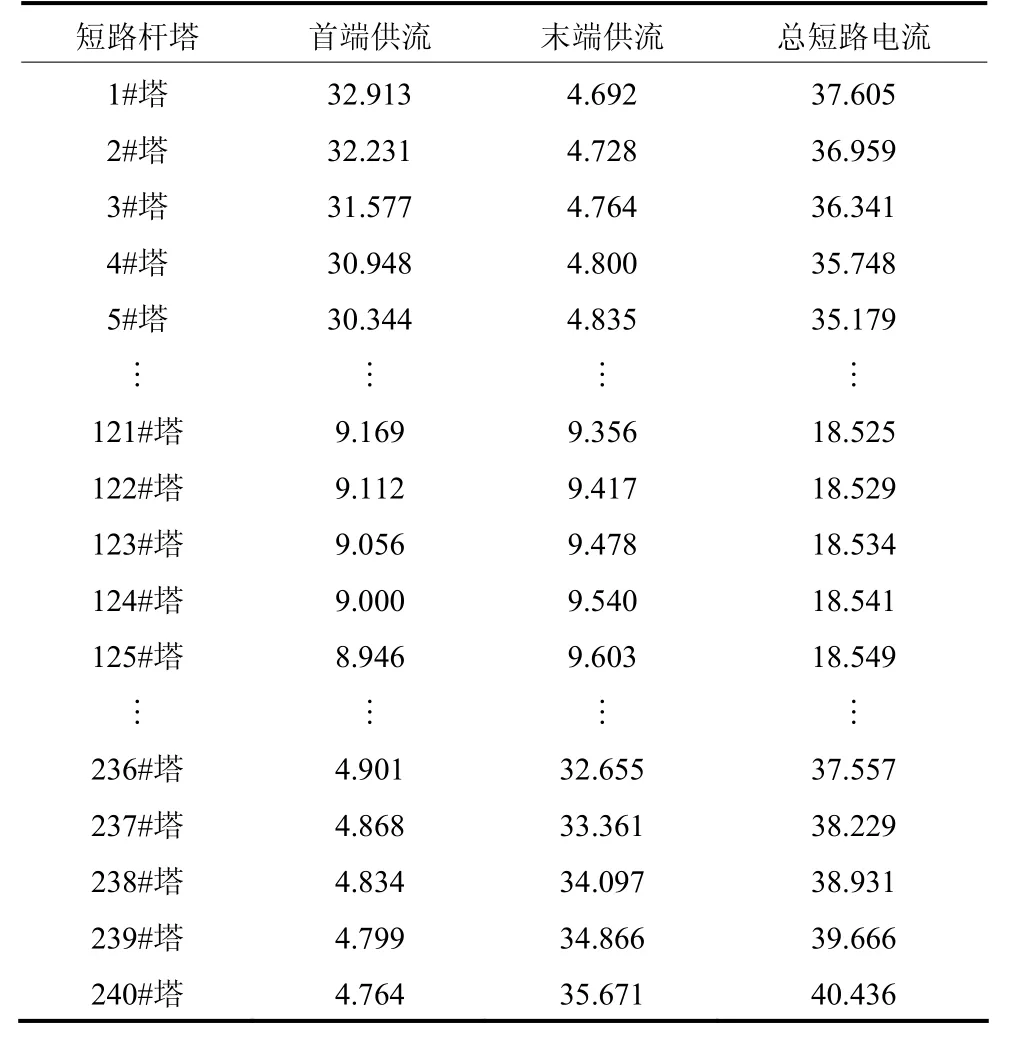
表3 各杆塔单相接地短路电流Table 3 Current with grounding fault at each towerkA

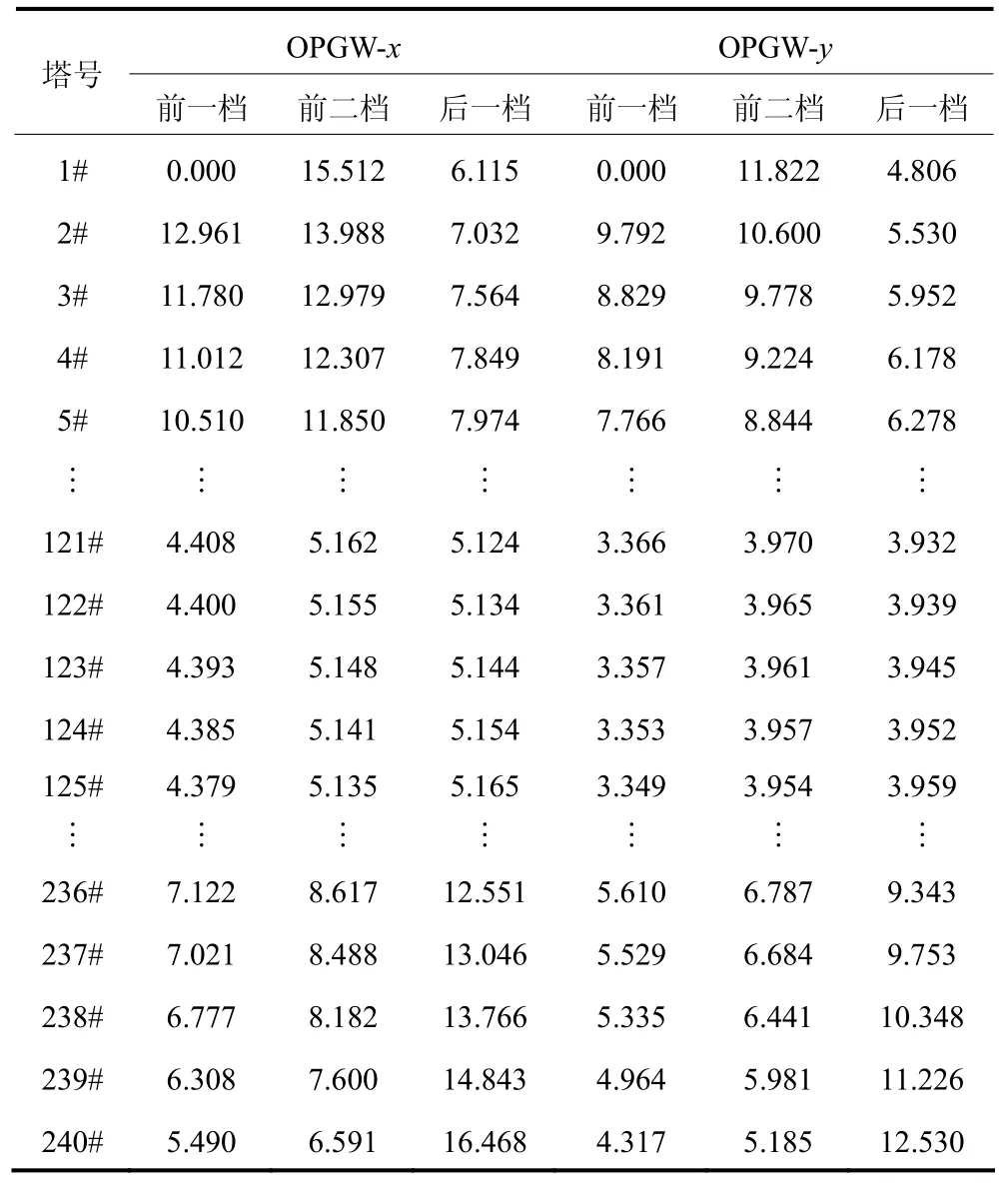
表4 OPGW 线短路电流Table 4 Fault current on OPGWkA

结合表3和表4分析，在第一级塔和最后一级塔上发生单相接地短路时，OPGW 能够起到较好的分流作用，有高达 80%的分流效果明显。在线路中间部分，OPGW 也有 50%的分流效果。总而言之，本工程算例的应用很好地说明本文的方法能够准确计算出架空输电线路的发生接地短路时，线路短路电流的分布情况和OPGW 线的分流系数。

3 结论

本文介绍了双 OPGW 的架空输电系统在复杂运行情况下，任一点发生接地短路后，基于相分量法的短路电流计算方法。该方法分别建立了接地短路发生在杆塔处和杆塔间的数学模型，形成了一套完整的计算体系，实用性强。同时，分别对接地短路发生在杆塔上和杆塔之间的情形进行了校验，并讨论了其在实际输电工程中的应用，能够准确计算出全线任一点发生接地短路时，相线和 OPGW 线上短路电流的分布情况，为 OPGW 线的校验选型和输电工程建设提供参考。

[1]赵建青, 姚瑶, 邱玩辉, 等. 基于输电线路在线巡视系统 的 智 能 预 警 系 统 研 究 [J]. 电 力 系 统 保 护 与 控 制 , 2013, 41(23): 49-54. ZHAO Jianqing, YAO Yao, QIU Wanhui, et al. Study on intelligent early warning system based on transmission line on-line inspection system[J]. Power System Protection and Control, 2013, 41(23): 49-54.

[2]杜天苍, 张尧, 夏文波. 利用短路电流热效应的 OPGW分流地线选型[J]. 高电压技术, 2007, 33(9): 110-114. DU Tiancang, ZHANG Yao, XIA Wenbo. Selection of the shunt ground wire of OPGW using thermal effect of short circuit current[J]. High Voltage Engineering, 2007, 33(9): 110-114.

[3]张国志, 张清枝. OPGW 工程测量技术探讨[J]. 电力系统保护与控制, 2009, 36(23): 130-132. ZHANG Guozhi, ZHANG Qingzhi. Discussion on measurement technology for OPGW projects[J]. Power System Protection and Control, 2009, 36(23): 130-132.

[4]张云鹏. 复杂结构输电线路接地短路及 OPGW 电流计算研究[D]. 郑州: 郑州大学, 2012. ZHANG Yunpeng. Compute and research on the complex structure transmission line grounding short-circuit and the current distribution of OPGW[D]. Zhengzhou: Zhengzhou University, 2012.

[5]王宇, 王建国, 彭向阳, 等. 220 kV 同塔双回输电线路架空地线感应电流与电能损耗[J]. 高压电器, 2013, 49(5): 31-38. WANG Yu, WANG Jianguo, PENG Xiangyang, et al. Overhead ground wires induction current and energy lossof 220 kV double circuit transmission lines[J]. High Voltage Apparatus, 2013, 49(5): 31-38.

[6]冯树海, 於益军, 王礼文, 等. 适用于拓扑调整的短路电流快速计算方法[J]. 电力系统保护与控制, 2014, 42(8): 28-33. FENG Shuhai, YU Yijun, WANG Liwen, et al. A method of fast short-circuit current calculation for topology adjustment[J]. Power System Protection and Control, 2014, 42(8): 28-33.

[7]顾秀芳, 王红坡. 基于相分量的配电网短路电流通用计算方法研究[J]. 电力系统保护与控制, 2011, 39(16): 80-82. GU Xiufang, WANG Hongpo. Research on general method for calculating short-circuit fault current of distribution network based on phase component[J]. Power System Protection and Control, 2011, 39(16): 80-82.

[8]梁睿, 杨学君, 薛雪, 等. 零序分布参数的单相接地故障 精 确 定 位 研 究 [J]. 电 工 技 术 学 报 , 2015, 30(12): 472-479. LIANG Rui, YANG Xuejun, XUE Xue, et al. Study of accurate single-phase grounding fault location based on distributed parameter theory using data of zero sequence components[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 472-479.

[9]DAWALIBI F. Ground fault current distribution between soil and neutral conductors[J]. IEEE Transactions on Power Apparatus and Systems, 1980, 99(2): 452-461.

[10]DAWALIBI F, NILES G B. Measurements and computations of fault current distribution on overhead transmission lines[J]. IEEE Transactions on Power Apparatus and Systems, 1984, 103(3): 553-560.

[11]蒋陶宁, 李军, 孙成秋, 等. 交流特高压输电线路复杂地线系统单相短路电流的计算[J]. 电网技术, 2011, 35(10): 16-21. JIANG Taoning, LI Jun, SUN Chengqiu, et al. Calculation of the single phase short-circuit current in complex ground system of UHV AC transmission lines[J]. Power System Technology, 2011, 35(10): 16-21.

[12]叶圣永, 程超, 唐权, 等. 基于 BPA 的短路电流计算模 式 研 究 [J]. 电 力 系 统 保 护 与 控 制 , 2015, 43(18): 138-143. YE Shengyong, CHENG Chao, TANG Quan, et al. Research on calculation mode of short-circuit current based on BPA[J]. Power System Protection and Control, 2015, 43(18): 138-143.

[13]邹军, 袁建生, 李昊, 等. 架空线路短路电流分布及地线屏蔽系数的计算[J]. 电网技术, 2000, 24(10): 27-30. ZOU Jun, YUAN Jiansheng, LI Hao, et al. Computation of fault current distribution and shielding coefficient of ground wires for overhead transmission lines[J]. Power System Technology, 2000, 24(10): 27-30.

[14]邹军, 袁建生, 周宇坤, 等. 统一广义双侧消去法与架空线路–地下电缆混合输电系统故障电流分布的计算[J]. 中国电机工程学报, 2002, 22(10): 112-115. ZOU Jun, YUAN Jiansheng, ZHOU Yukun, et al. Uniform generalized double-sided elimination method and the calculation of the fault current distribution for hybrid overhead-underground power lines[J]. Proceedings of the CSEE, 2002, 22(10): 112-115.

[15]潘启军, 孟庆云, 张向明, 等. 基于互感参数提取的多导体与多导线模型缩减方法研究[J]. 电工技术学报, 2015, 30(8): 289-296. PAN Qijun, MENG Qingyun, ZHANG Xiangming, et al. A model reduction study of multiple conductors and multiple wires based on extraction of mutual inductance parameters[J]. Transactions of China Electrotechnical Society, 2015, 30(8): 289-296.

[16]刘赟, 俞集辉, 程鹏. 基于电磁-热耦合场的架空输电线 路 载 流 量 分 析 与 计 算 [J]. 电 力 系 统 保 护 与 控 制 , 2015, 43(9): 28-34. LIU Yun, YU Jihui, CHENG Peng. Analysis and calculation on the ampacity of overhead transmission lines based on electromagnetic-thermal coupling fields[J]. Power System Protection and Control, 2015, 43(9): 28-34.

[17]电力工程高压送电线路设计手册[M]. 北京: 中国电力出版社, 2003.

[18]袁涛, 唐妍, 司马文霞, 等. 短导体对水平接地极冲击特性的影响[J]. 电工技术学报, 2015, 30(1): 177-185. YUAN Tao, TANG Yan, SIMA Wenxia, et al. Simulation analysis of the impact characteristic of grounding electrode based on the current shielding effect[J]. Transactions of China Electrotechnical Society, 2015, 30(1): 177-185.

[19]黎鹏, 崔健, 付杰. 架空输电线任一点不对称短路时OPGW 线路电流的分布研究[J]. 华北电力大学学报, 2014, 41(4): 56-60. LI Peng, CUI Jian, FU Jie. Analysis of asymmetric short-circuit current distribution in OPGW overhead transmission line system[J]. Journal of North China Electric Power University, 2014, 41(4): 56-60.

[20]吴田, 胡毅, 刘凯, 等. 复合光纤架空地线在不同接地方 式 下 的放电路径选择 特 性[J]. 高 电 压 技 术, 2012, 38(4): 878-884. WU Tian, HU Yi, LIU Kai, et al. Discharge path selective probability of optical fiber composite overhead ground wire at different ground methods[J]. High Voltage Engineering, 2012, 38(4): 878-884.

Research of current distribution between OPGWs in overhead transmission system with grounding fault at any point

QI Zheng1, RAO Zhi1, YANG Linlin2
(1. School of Electric and Electronic Engineering, North China Electric Power University, Beijing 102206, China; 2. State Grid Beijing Electric Power Company, Beijing 100031, China)

Fault currents distributed on optical composite overhead grounding wire (OPGW) have a significant influence on the safe operation of the overhead transmission system. Traditional calculation methods include simplified calculation method and sequence component method. These two only focus on the grounding fault at one of the power towers. Owing to much ignorance, the calculation results are too simplified and not reliable. To solve these problems, this paper discusses the calculation of the grounding fault current distributed on OPGW at any point of the transmission line based on phase component method. The whole line can be divided into different sections by each power tower. Separately, two mathematic modulations are built when the grounding fault at tower and between towers. Numerical examples are applied to verify the correctness of theories of fault at the tower, and then the results are used to verify the correctness of fault between towers, finally applied into an actual project. In the complex overhead transmission system with OPGWs, phase component method proposed can accurately calculate the current distribution with grounding fault at any point of the line. This work is supported by National Natural Science Foundation of China (No. 51277066).

optical fiber composite overhead grounding wire; overhead transmission line; power tower; grounding fault at any point; fault current distribution

TM77

1674-3415(2016)02-0086-09

2015-04-08；

2015-07-02

齐郑(1977-)，男，博士，副教授，研究方向为电力系统分析与控制、配网自动化、输配电技术等；E-mail: qizheng319@126.com

(编辑 周金梅)

国家自然科学基金项目(51277066)

饶 志(1990-)，男，通信作者，硕士研究生，研究方向为电力系统分析与控制、输配电技术。E-mail: sibeiti@126. com