基于响应面法的轿车主减速齿轮可靠性灵敏度研究

梁明轩　 王晓林 　袁惠群 　于印鑫

1. 中国计量学院, 杭州, 310018　2. 东北大学, 沈阳, 110819 3.昆明理工大学， 昆明，650500

基于响应面法的轿车主减速齿轮可靠性灵敏度研究

梁明轩1王晓林1袁惠群2于印鑫3

1. 中国计量学院, 杭州, 3100182. 东北大学, 沈阳, 110819 3.昆明理工大学， 昆明，650500

摘要：为获得某轿车主减速齿轮尺寸参数对其传动可靠性的影响，提出采用改进拉丁超立方抽样(LHS)获取随机尺寸样本的方法；通过显式有限元仿真构建齿面最大接触应力完全二次响应面(RSM)，研究了可靠度对参数的灵敏度。结果表明主减速齿轮可靠度对压力角和模数的均值与方差较为敏感，应合理控制其取值。

关键词：主减速齿轮；改进拉丁超立方抽样；完全二次响应面；可靠性灵敏度

0引言

汽车变速器是影响汽车性能的关键部件之一，其内部主减速齿轮副处于常啮合状态，承受着整车的全部驱动负载，且工况复杂多变，一旦出现故障不容易替换，该齿轮副的动力稳健性将会直接影响到整车的耐久性和可靠性等性能指标[1-3]。影响齿轮副接触应力的因素有很多，采用蒙特卡罗(MonteCarlo)模拟齿轮接触应力分布时，需将不确定因素作为随机变量建立概率模型，此时样本抽样方法对于近似响应面模型的建立至关重要[4]。近20年来，拉丁超立方抽样方法已广泛应用于预测模式的参数不确定性分析中[5-7]。为了用较少的样本有效地估计响应变量的均值，McKay等[5]提出了中值拉丁超立方抽样(medianLatinhypercubesampling,MLHS)方法，它可以在抽取较少样本的情况下，获得较高的计算精度。Jirutitijaroen等[6]提出了含随机排序法的拉丁超立方抽样(LHSwithrandompermutation,LHSRP)方法，该方法需要准备足够数量的素数并考虑素数的根逆转换，以上方法均没有考虑抽样参数的概率分布尾部特征。

目前，机械零件可靠性灵敏度分析大多以单个一体化结构的振动响应量作为极限状态函数[8-11]，对于含有齿轮耦合接触非线性的可靠度灵敏性分析在文献中鲜见。文献[8]采用不含交叉项的纯二次多项式响应面法对翼梁结构的强度可靠度进行计算，获得了机翼腹板和上下缘线等基本变量参数对结构的可靠性灵敏度。文献[9]将6σ可靠性方法与协同优化相结合研究了汽车车桥轻量化问题，表明协同优化方法得到的最优解提高了系统的可靠性。王新刚等[10]重点考虑零件可靠度和失效率受变载荷和强度退化的影响，分析了管形截面扭杆在时变载荷作用下的动态可靠性灵敏度。

事实上，由于设计公差、制造误差和啮合磨损等因素影响，汽车主减速齿轮副尺寸分布具有一定的随机性，此时按确定性设计的齿轮副仍有可能发生疲劳失效。为体现参数分布的重要性，本文首先改进了LHS抽样，利用显式动态有限元程序仿真获得了不同参数样本下主减速齿轮副啮合三维接触应力，从而构建了齿面接触极限状态完全二次多项式显式响应面，计算了主减速齿轮副在随机尺寸参数影响下的可靠度，并对影响啮合可靠性的基本随机变量的灵敏度进行了分析，该方法和研究结果能较好地用于轿车主减速齿轮副结构优化。

1改进的拉丁超立方重要性抽样

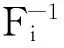
x1,in=Fi-1((n-0.5)/N)

(1)

采用子区间随机抽样的LHSRP法样本点x2,in可表示为

x2,in=Fi-1(ri,n/N+(n-1)/N)

(2)

式中，ri,n为[0,1]内的独立伪随机数，n=1,2,…,N。

当采用LHIS法抽样时，抽取概率密度曲线期望左边子区间的右边界点，抽取期望值右边子区间的左边界点，这样就保证抽取更多的期望值附近样本点，更接近实际样本分布特征，其样本点x3,in可以表示为

(3)

采用MLHS法、LHSRP法和LHIS法的抽样过程如图1a和图1b所示，对于样本Xi服从期望为4、标准差为2的正态分布的6次抽样结果如图1c和图1d所示。可以看出MLHS法和LHSRP法抽样更侧重于在子区间内取点，体现了“分层”的思想，而LHIS法的关键在于选取子区间内趋近期望值的边界顶点，兼顾了“分层”和“重要性”的思想，从而使抽样结果能更好地体现样本实际分布，具有较高的收敛性。

(a)MLHS、LHSRP法概率分布曲线

(b)LHIS法概率密度曲线

(c)MLHS、LHSRP法的抽样结果(d)本文LHIS法的抽样结果图1　MLHS、LHSRP和LHIS方法的样点比较图

2主减速齿轮三维啮合应力响应面

2.1响应面模型理论

响应面法(responsesurfacemethodology,RSM)是通过一系列确定性的试验拟合一个响应面来模拟真实极限状态曲面的方法。响应面法作为经典的代理模型方法包括线性响应面、加权非线性响应面、高精度响应面以及Kriging响应面等[11-12]，本文采用显式完全二次多项式响应面拟合隐式极限状态函数，便于通过求可靠度显式表达式的偏导数获得系统的可靠性灵敏度。假设n维随机输入变量x和响应向量y之间具有如下近似关系：

(4)

式中，a0、ai、aij(i=1,2，…,n; j=i,i+1,…,n)为待定系数。

对输入变量x的k个样本值(x1,x2,…,xk)进行仿真试验，得到k个响应量(y1,y2,…,yk)，则样本点试验值与近似响应面值之间的误差可以表示为

(5)

利用最小二乘法对式(5)进行回归分析，使误差项最小，则可以得到

(6)

通过对式(6)进行求解可以得到系统基本随机变量和结构响应值的近似关系式中各系数的估计值，从而得到响应面函数的显式表达式。

2.2基于显式有限元法的齿轮啮合仿真

某型国产变速器主减速器输入齿轮齿数z1=15，输出齿轮齿数z2=65，一挡工况输入转速w=95.993 rad/s，额定扭矩T=1545.818N·m。在主减速齿轮副的尺寸范围内，假设齿宽、螺旋角、压力角和模数服从正态分布，各变量的取值全部集中在[μ-3σ, μ+3σ]，样本分布均满足3σ准则，其均值和标准差如表1所示。

表1　主减速齿轮尺寸变量均值和标准差

齿面出现最大接触应力是齿轮出现点蚀失效的直接原因，为了构建接触应力响应面模型，首先利用LHIS法对主减速齿轮副尺寸随机变量进行抽样，得到仿真样本点，利用ABAQUS/Explicit显式动态有限元程序仿真得到每组样本点齿面最大接触应力值。

图2为某型主减速齿轮副有限元模型，分别在两齿轮轴心建立参考点RP-1与RP-2，建立如图2所示坐标系，将齿轮内圈与参考点完全耦合，通过参考点施加边界条件和载荷，约束参考点x、y、z方向位移以及绕x、y轴的旋转，保留绕z轴旋转自由度；在RP-1点上施加转速ω，在RP-2上施加负载扭矩T，仿真时间为20 ms，取齿面最大应力作为响应真实值。

图3为样本初始取值时齿面最大接触应力云图，可以看出在动态啮合过程中齿面最大接触应力为947.62 MPa。

图 2　ABAQUS/Explicit中主减速齿轮有限元模型

图 3　初始样本值下齿轮接触应力云图

利用式(4)～式(6)进行数据回归分析可以得到主减速齿轮副接触应力响应面模型，其系数如表2所示。

表2　响应面函数系数项

3主减速器齿轮啮合可靠性及灵敏度分析

3.1可靠性分析及可靠度

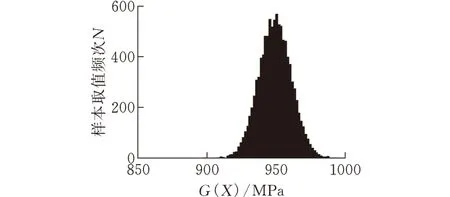
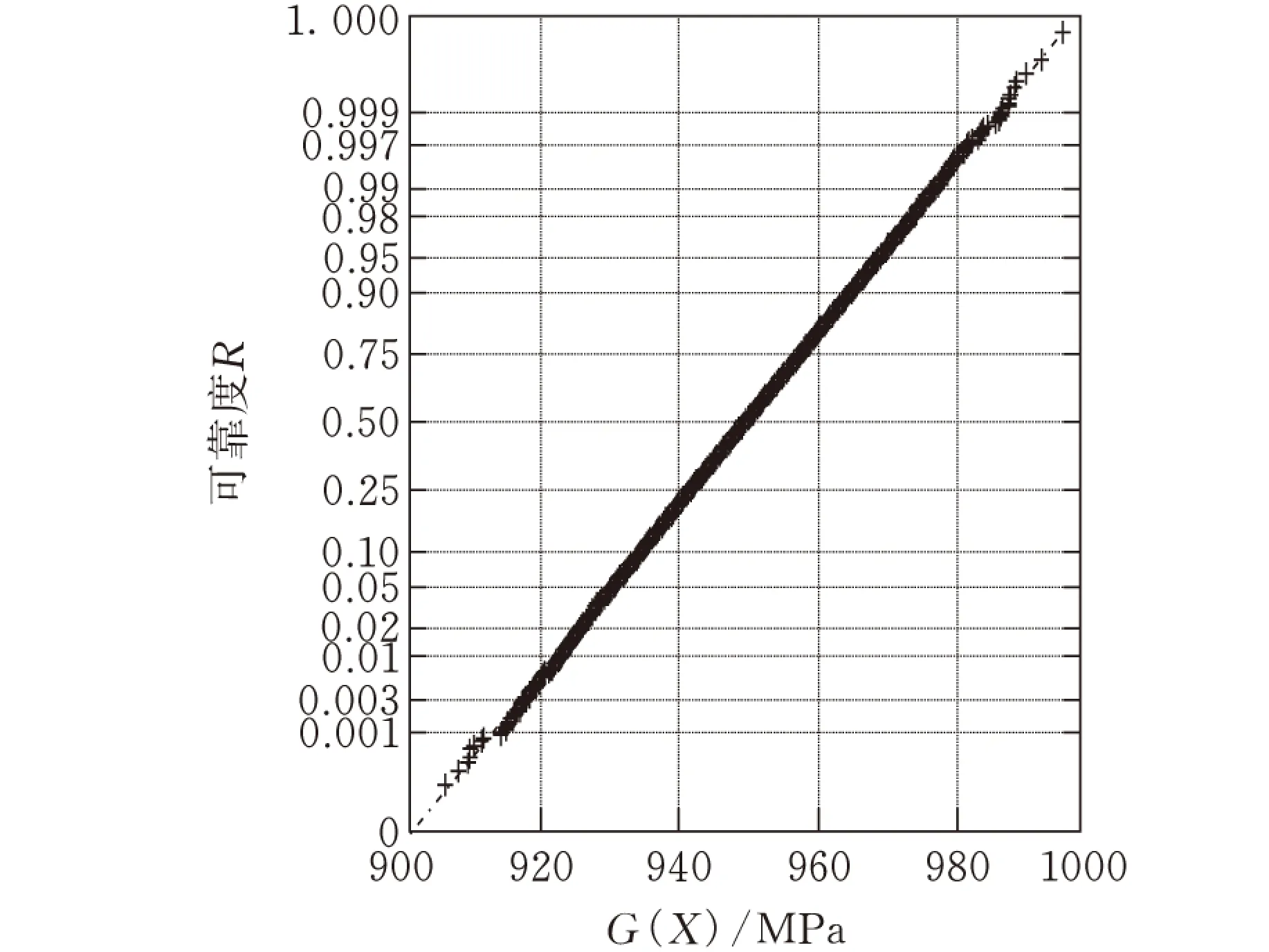
假设Pmax为主减速器齿轮副齿面许用接触应力强度因子，G(X)是接触状态响应面函数，齿轮接触存在两种状态：G(X)≥Pmax失效状态；G(X)

μG=E(G(X))=μG(μ1,μ2,…,μk,D1,D2,…,Dk)

(7)

DG=D(G(X))=DG(μ1,μ2,…,μk,D1,D2,…,Dk)

(8)

由此可以得到状态函数的可靠性指标表达式为

(9)

对于任意分布的状态函数可以采用蒙特卡罗法模拟得到其分布特征参数，若G(X)服从正态分布，则系统可靠度可表示为R=ψ(β)，其中ψ(·)为标准正态分布[10]。取设计要求的主减速齿轮啮合极限接触强度因子Pmax=985 MPa。图4为利用蒙特卡罗法通过2000次模拟得到的主减速齿面最大接触应力响应状态函数G(X)概率直方图和正态概率图。从图4可以看出G(X)服从正态分布，得到状态函数均值和标准差为：μG=949.4799 MPa，σG=351.6672 MPa。通过式(9)计算得到β=2.70，从而得到其可靠度R=0.9965。

(a)状态函数G(X)概率直方图

(b)状态函数G(X)正态概率图图 4　主减速齿轮副最大接触应力函数概率分布图

3.2主减速器接触可靠性灵敏度分析

参数的灵敏度分析是确定各参数对模式预测结果的贡献大小，均值灵敏度反映了样本均值大小对可靠性的影响程度，方差灵敏度反映了样本参数波动性对可靠性的影响程度，它有利于在进一步的研究过程中有效减小模式预测参数的不确定性程度。主减速齿轮接触强度可靠度对基本随机变量的均值和方差的灵敏度为

(10)

(11)

利用式(10)和式(11)将μG和DG对矩阵μ和D中各元素求偏导数，略去求解过程，得到

4结论

(1)利用改进的拉丁超立方抽样对某型主减速齿轮副基本结构尺寸进行了抽样，采用完全二次多项式显式响应面法对其接触可靠性进行了分析。

(2)在主减速齿轮副基本尺寸样本服从正态分布的情况下，由蒙特卡罗法模拟得到的最大齿面接触应力服从正态分布。主减速齿轮副模数分布是影响其可靠性的最主要因素；压力角和模数均值的增大会降低其接触可靠度，齿宽和螺旋角的增大会增大其可靠度；基本尺寸随机波动对其接触可靠性影响相对较小。该方法可为轿车主减速齿轮啮合传动优化设计提供参考。

参考文献：

[1]Rao S S, Tjandra M .Reliability-based Design of Automotive Transmission Systems[J]. Reliability Engineering & System Safety, 1994, 46(2): 159-169.

[2]李昌, 韩兴. 基于响应面法齿轮啮合传动可靠性灵敏度分析[J]. 航空动力学报, 2011, 26(3): 711-715.

Li Chang, Han Xing. Analysis of Reliability Sensitivity for Gear Engagement Based on Response Surface Methods[J]. Journal of Aerospace Power, 2011, 26(3): 711-715.

[3]尚蛟, 冯慧华, 鲁守卫, 等. 轿车变速器主减速器齿轮副动态性能仿真[J]. 振动工程学报, 2010, 23(6): 665-669.

Shang Jiao, Feng Huihua, Lu Shouwei. et al. Simulation Research on Dynamic Performance for Gear Pair of Main Gear Box in Transmission of a Car[J]. Journal of Vibration Engineering, 2010, 23(6): 665-669.

[4]Hosseini S A A, Khadem S E. Vibration and Reliability of a Rotating Beam with Random Properties under Random Excitation[J]. International Journal of Mechanical Sciences, 2007, 49(12): 1377-1388.

[5]Mckay M D, Beckman R J, Conover W J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code[J]. Technometrics, 1979, 21(2): 239-245.

[6]Jirutitijaroen P, Singh C. Comparison of Simulation Methods for Power System Reliability Indexes and Their Distributions[J]. IEEE Transactions on Power Systems, 2008, 23(2): 486-493.

[7]Echard B, Gayton N, Lemaire M. AK-MCS: an Active Learning Reliability Method Combing Kriging and Monte Carlo Simiulation[J]. Structural Safety, 2011, 33(2): 145-154.[8]高宗战, 刘志群, 姜志峰, 等. 飞机翼梁结构强度可靠性灵敏度分析[J]. 机械工程学报, 2010, 46(14): 194-198.

Gao Zongzhan, Liu Zhiqun, Jiang Zhifeng, et al. Strength Reliability and Parameter Sensitivity Analysis for Airfoil Spar Structure[J]. Journal of Mechanical Engineering, 2010, 46(14): 194-198.

[9]姜武华, 王其东, 何炜, 等. 基于可靠性的车桥结构多学科优化[J]. 汽车工程, 2012, 34(12): 1136-1140.

Jiang Wuhua, Wang Qidong, He Wei, et al. Reliability-based Multidisciplinary Optimization of Vehicle Axle Structure[J]. Automotive Engineering, 2012, 34(12): 1136-1140.

[10]王新刚, 张义民, 王宝艳. 机械零部件的动态可靠性灵敏度分析[J]. 机械工程学报, 2010,46(10): 188-193.

Wang Xingang, Zhang Yimin, Wang Baoyan. Dynamic Reliability Sensitivity Analysis of Mechanical Components[J]. Journal of Mechanical Engineering, 2010,46(10): 188-193.

[11]吕震宙, 宋述芳, 李红双, 等. 结构机构可靠性及可靠性灵敏度分析[M]. 北京: 科学出版社, 2009.

[12]吕震宙, 赵洁, 岳珠峰. 机械可靠性分析的高精度响应面法[J]. 应用数学和力学, 2007, 28(1):16-24.

Lü Zhenzhou, Zhao Jie, Yue Zhufeng. Advanced Response Surface Method for Mechanical Reliability Analysis[J]. Applied Mathematics and Mechanics, 2007, 28(1):16-24.

(编辑王艳丽)

ReliabilitySensitivityforMainReductionGearsofaCarBasedonResponseSurfaceMethods

LiangMingxuan1WangXiaolin1YuanHuiqun2YuYinxin2

1.ChinaJiliangUniversity,Hangzhou， 3100182.NortheasternUniversity,Shenyang,1108193.KunmingUniversityofScienceandTechnology,Kunming,650500

Abstract：In order to obtain the effects of size parameters on reliability of the main reduction gears in a car, an improved LHS was presented to acquire the random size samples. The full quadratic RSM of the maximum contact stress on tooth surface was built through explicit finite element simulations to study reliability sensitivity to the key parameters. The results show that the mean and variance of pressure angle and modulus which are more sensitive to reliability of the gears must be selected reasonably in design stage.

Key words：main reduction gear; improved Latin hypercube sampling; full quadratic response surface model; reliability sensitivity

收稿日期：2015-05-04

基金项目：国家高技术研究发展计划(863计划)资助项目(2012AA040104);浙江省“仪器科学与技术”重中之重学科开放基金资助项目

中图分类号：TK122

DOI：10.3969/j.issn.1004-132X.2016.04.023

作者简介：梁明轩，男，1986年生。中国计量学院机电工程学院讲师。研究方向为齿轮箱传动系统动力学及其可靠性、转子系统非线性动力学及振动控制。发表论文6篇。王晓林，男，1957年生。中国计量学院机电工程学院教授。袁惠群，男，1954年生。东北大学理学院教授、博士研究生导师。于印鑫，男，1983年生。昆明理工大学机电工程学院讲师。