基于粒子群优化支持向量机的注水井吸水剖面预测*
2016-06-23李俊键周代余丁帅伟姜汉桥张曙振旷曦域
李俊键 周代余 赵 冀 丁帅伟 姜汉桥 张曙振 梁 彬 旷曦域 王 倩
(1. 中国石油大学(北京)石油工程教育部重点实验室 北京 102249; 2. 中国石油塔里木油田分公司勘探开发研究院 新疆库尔勒 841000)
基于粒子群优化支持向量机的注水井吸水剖面预测*
李俊键1周代余2赵 冀2丁帅伟1姜汉桥1张曙振2梁 彬1旷曦域2王 倩2
(1. 中国石油大学(北京)石油工程教育部重点实验室 北京 102249; 2. 中国石油塔里木油田分公司勘探开发研究院 新疆库尔勒 841000)
李俊键,周代余,赵冀,等.基于粒子群优化支持向量机的注水井吸水剖面预测[J].中国海上油气,2016,28(5):66-70.
Li Junjian,Zhou Daiyu,Zhao Ji,et al.Prediction of water injection profile based on particle swarm optimization-support vector machine[J].China Offshore Oil and Gas,2016,28(5):66-70.
注水井吸水剖面预测对于分层注水调整方案的编制和注采井组水淹状况的确定具有重要的指导意义。历史吸水剖面是目前最准确的计算分层吸水量的资料,但是目前对于该资料的使用并不是很全面,多因吸水剖面资料过少,或插值方法选取过于简单。本文在历史吸水剖面资料的基础上,利用粒子群优化支持向量机方法,通过回归拟合历史吸水剖面资料,建立了吸水剖面预测模型,实现了无吸水剖面时间点注水井吸水剖面的预测,从而达到准确劈分注水量的目的。实例应用结果表明本文方法考虑了各种影响小层吸水的动静态因素,预测结果准确可靠,可用于注水井分层注水量的劈分研究。
吸水剖面预测;支持向量机;粒子群算法;回归预测模型
对于注水开发油田,特别是在注水开发后期,由于油藏平面上和纵向上的非均质及油水黏度的差别、注采井组内部的不平衡及注入水的长期冲刷,造成注入水在平面上向生产井方向的舌进现象和纵向上向高渗透层的突进现象,从而使注入水无效循环而影响注水效果。此外,在编制分层注水调整方案时,首先要知道目的层的注水效果,然后才能根据油水井的动态变化确定具体注水层段调整意见。
长期以来,注水井吸水剖面预测是计算注水井分层注水量和累计吸水量的重要依据,对每口注水井进行小层吸水量的劈分是在注水油田开发中后期研究注采井组的水淹状况和驱油效率最重要的环节[1]。关于注水井小层吸水剖面预测的计算,目前主要有渗流力学计算方法、劈分系数法、吸水剖面插值法和数值模拟法[1-5]。其中,传统的渗流力学方法多为KH法,该方法没有充分考虑储层的连通性、压差、物质平衡和能量平衡,其计算结果不能反映地下的实际注水情况;劈分系数法虽然考虑的因素较多,但是建立的吸水剖面和影响因素之间的关系多为线性关系,不太符合生产实际情况;吸水剖面插值法是目前最准确的一种方法,但吸水剖面资料的多少和插值方法的选取会影响劈分的精度,而海上油田测试成本较高,实际的吸水剖面资料并不多;数值模拟法虽然使用比较方便,但其准确性须建立在精确的地质模型和较高质量的历史拟合基础之上,工作量较大。本文提出了利用粒子群优化支持向量机方法,通过回归拟合历史吸水剖面资料,建立吸水剖面预测模型,实现未知时间点注水井吸水剖面的预测,从而达到准确劈分注水量的目的,并进行了实例应用。
1 支持向量机回归及粒子群优化原理
1.1 支持向量机回归原理
支持向量机方法(SVM)是20世纪90年代初Vapnik等[6]根据统计学习理论提出的一种新的机器学习方法,它以结构风险最小化原则为理论基础,通过适当地选择函数子集及该子集中的判别函数,使学习机器的实际风险达到最小。该算法的优势在于可以对小样本数据进行较好的回归预测,与神经网络模型以及其他常规的回归方法相比具有样本需求量少、回归精度高的特点。

(1)
式(1)中右侧第1项是使回归函数更为平坦,泛化能力更好;第2项则为减少误差;常数C>0为罚系数。本文选用径向基函数exp(g|xi-xj|2)作为核函数。
1.2 粒子群优化算法原理
粒子群算法(PSO)是模拟鸟群觅食行为的一种基于迭代的最优化算法,是Eberhart等[8]提出的。设粒子群的种群规模为M,决策空间n维,第i个粒子在n维的位置表示为xi=(xi1,xi2,…,xin),飞行速度为vi=(vi1,vi2,…,vin)。经过评价函数可以得到每个粒子的适应度值,第i个粒子到目前为止得到最优的适应度值时所在位置为pi=(pi1,pi2,…,pin),也记为pbest;整个粒子群到目前为止得到最优的适应度值时所在位置为gi=(gi1,gi2,…,gin),也记为gbest。在找到这2个最优值后,可以根据以下策略更新每个粒子的速度和位置:
vi(t+1)=wvi(t)+c1r1(pi(t)-
xi(t))+c2r2(pg(t)-xi(t))
(2)
xi(t+1)=xi(t)+vi(t+1)
(3)
式(2)、(3)中:t为当前迭代次数;w为惯性权值;c1、c2为加速因子,是非负常数;r1和r2是[0,1]范围内的随机数。对于标准粒子群算法,w=0.721,c1=c2=1.193[9]。
2 吸水剖面预测模型的建立
文献[10-12]研究表明,支持向量机模型回归精度与惩罚因子C和径向基函数的g值均存在一定的关系,为了获取最佳回归性能的支持向量机模型,需要得到最佳的C和g值。如果采取穷举的方式搜索最优值,计算量会十分巨大甚至无法实现。由于粒子群优化算法具有隐含的并行性和强大全局搜索能力,可以在很短的时间内搜索到全局最优点,因此本文利用粒子群优化算法优化支持向量机中的C和g这2个参数,提出了粒子群优化支持向量机回归预测吸水剖面模型(PSO-SVM)的具体流程图(图1),具体步骤如下。
1) PSO和SVM初始化。设置终止迭代次数Tmax和种群数量N,令当前迭代次数t=1。在定义空间Rn中随机产生N个粒子的位置x1,x2,…,xN,组成初始种群X(t);随机产生各粒子的初始速度v1,v2,…,vN,组成初始种群V(t)。设定SVM精确度ε和参数C及g的寻优区间。
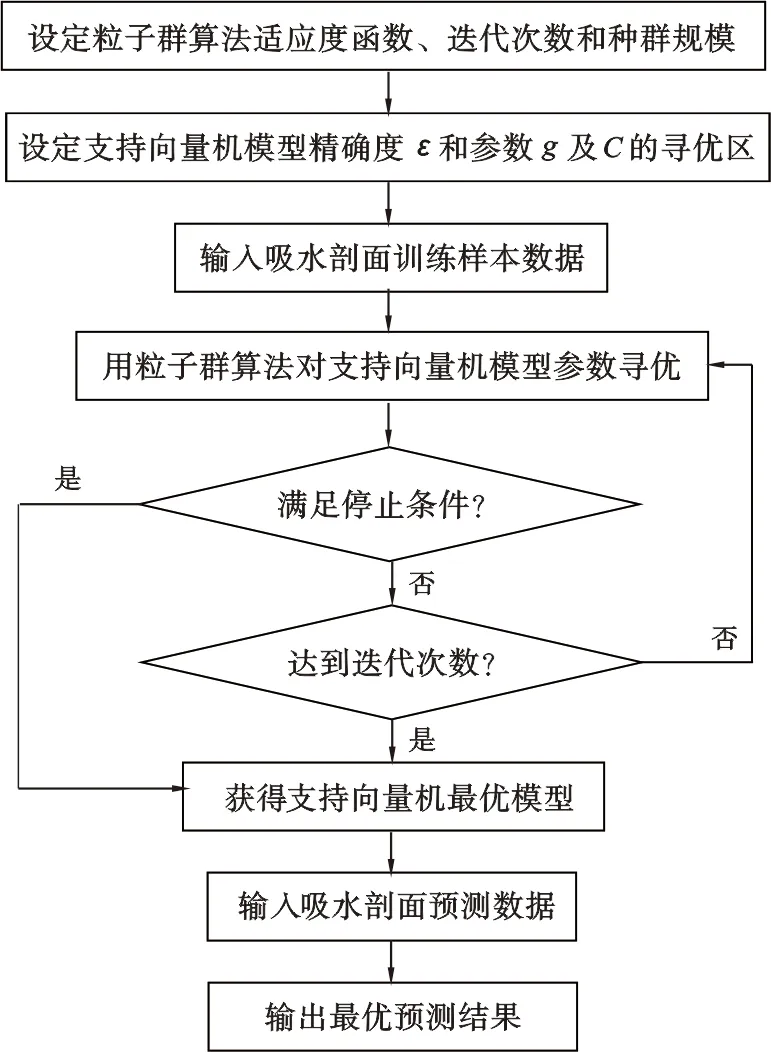
图1 粒子群优化支持向量机回归预测吸水剖面模型流程

3) 按照式(2)和式(3)更新粒子的速度和位置,产生新种群X(t+1)和V(t+1)。
4) 检查结束条件,满足时结束寻优,否则令t=t+1,转至步骤2)。结束条件为寻优达到最大迭代次数Tmax。
5) 将寻到的粒子最优位置即最优参数向量(C,g)赋给SVM。
6) 用吸水剖面样本数据对SVM进行训练,得到最优吸水剖面回归预测模型。
3 实例应用
A油田为块状底水中低渗砂岩油藏,1990年11月投入生产,1994年5月开始采用一套开发层系、一套井网进行整体注水开发。经过多年的注水开发,油藏已经发育优势渗流通道,急需了解油藏的分层吸水和水淹状况。以该油田一口注水井(B井)为例,说明如何使用本文建立的PSO-SVM回归预测模型进行吸水剖面的预测,进而实现该井分层注水量的劈分。
B井于1995年6月开始注水,注水层位为10个小层。考虑到影响吸水剖面的地质因素和开发因素[4],根据已有文献中动态劈分系数法采用的影响因素[1-2,4-5],并结合目标油田的实际情况和因素获取的难易程度,本次选取注水井对应的生产井开关井数、注采井距、开采厚度、月总注入量、层段渗透率、沉积微相影响系数、有效厚度和渗透率级差等8个影响因素,建立了B井的吸水剖面样本点。
本文预测模型的建立是分层进行的,因为每一层的吸水量是根据总注水量乘以吸水剖面得到的,所有层的吸水量之和等于总的注水量,另外分层模型建立的因素中考虑了层间干扰的一些因素,如开采厚度等,因此吸水剖面的计算实际上考虑了层与层之间的干扰问题,虽然是一层一层处理的,但实际上层与层之间是相关联的。以B井第4层为例进行具体说明,该层吸水剖面资料从1996年7月到2013年2月共有39个样本点,为了验证本文方法的准确性和可靠性,选取前面的35个样本作为输入样本,后面的4个样本作为验证样本。表1为B井第4层吸水剖面样本点。
图2为B井适应度函数随粒子群迭代次数的变化曲线,最终可得到最优的C和g值分别为27.588 4和0.088 692,最优适应度值为0.717 66。图3为B井回归预测数据和样本点的拟合曲线图,可以看出回归预测模型的拟合精度较高,均方误差为0.154 746,相关系数达0.919 051。
通过统计表1中的回归预测值和样本值的误差,得到回归样本点(前35个)的平均误差为2.38%,预测样本点(后4个)的平均误差为7.07%,误差都在允许范围之内。将其他月份数据代入该层的PSO-SVM吸水剖面回归预测模型,可以预测得到该井历史上每个月在该层的吸水量。同理,对其他小层采取同样的操作,从而完成B井所有小层吸水量的预测,最后再进行归一化处理,得到该井在历史上所有年份的吸水剖面。

表1 B井第4层吸水剖面样本点
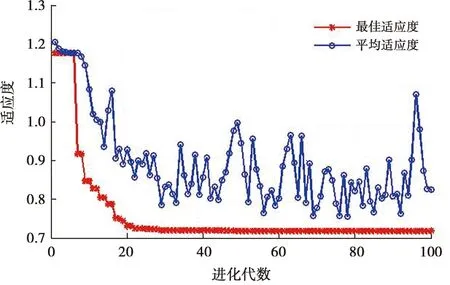
图2 B井适应度变化曲线
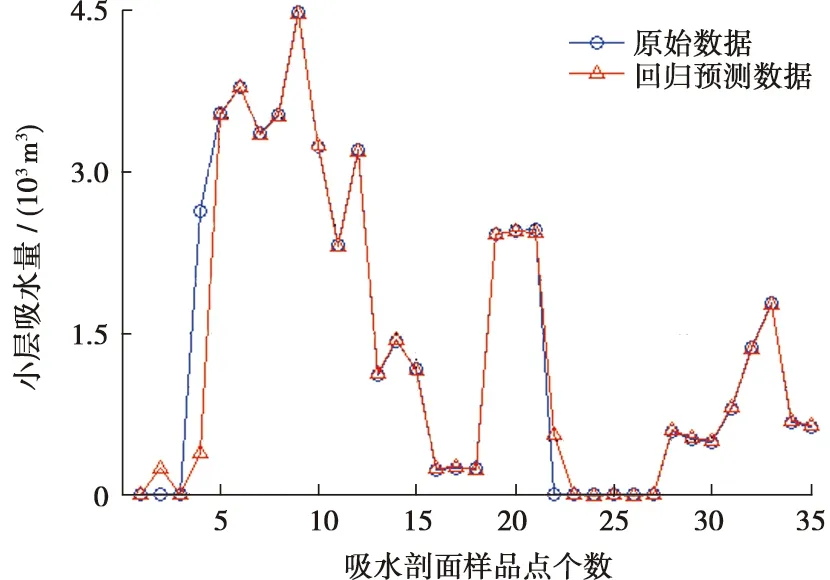
图3 B井回归预测曲线和原始数据对比
图4为利用PSO-SVM吸水剖面预测模型和数值模拟法分别劈分出来的B井分层累计吸水量对比图。从图4可以看出,PSO-SVM吸水剖面预测模型的劈分结果和数值模拟的劈分结果差别不大,由此证明该预测模型的劈分结果可以代替数值模拟的结果,但花费的人工时和工作量却大大降低。
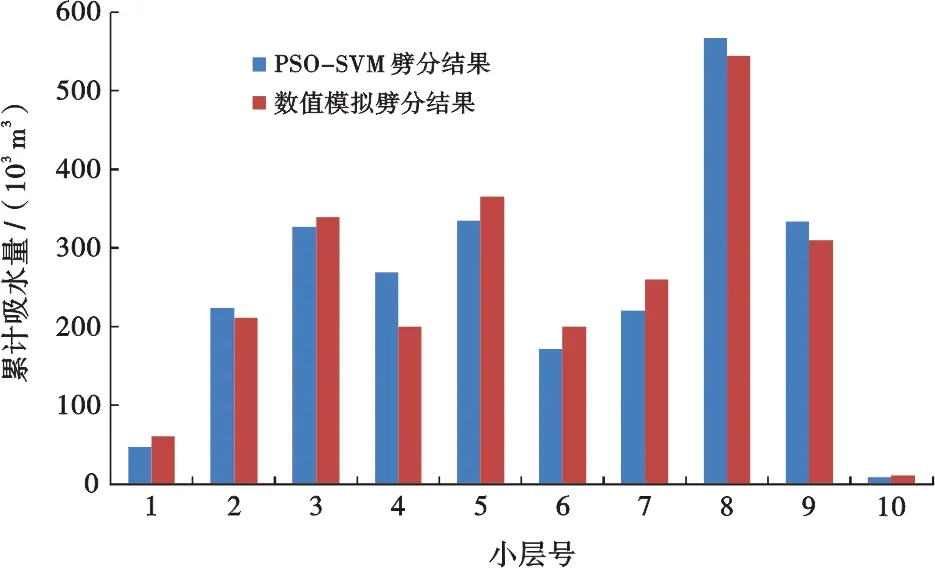
图4 B井PSO-SVM和数值模拟累计注水量劈分结果对比
4 结论
基于粒子群优化支持向量机方法,利用历史吸水剖面资料,建立了吸水剖面回归预测模型,实现了无吸水剖面时间点注水井吸水剖面的预测。实例应用结果表明,对无注水剖面资料的水井所建立的PSO-SVM回归预测模型考虑了各种影响小层吸水的动静态因素(如注水井对应的生产井开关井数、注采井距、开采厚度、月总注入量、层段渗透率、沉积微相影响系数、有效厚度和渗透率级差等),本文方法的劈分结果准确可靠,可以近似代替数值模拟劈分结果,但花费的人工时和工作量却得到了大大降低。
[1] 黄学峰,李敬功,吴长虹,等.注水井分层累计吸水量动态劈分方法[J].测井技术,2005,28(5):465-467. Huang Xuefeng,Li Jinggong,Wu Changhong,et al.Dynamic division method of accumulated injected-water volume for water-injected well[J].Well Logging Technology,2005,28(5):465-467
[2] 熊昕东,杨建军,刘坤,等.运用劈分系数法确定注水井单井配注[J].断块油气田,2004,11(3):56-59.Xiong Xindong,Yang Jianjun,Liu Kun,et al.Determination of water injection rate for single injection well employing dividing coefficient approach[J].Fault-Block Oil & Gas Field,2004,11(3):56-59
[3] 吴家文,宋考平,王一民,等.注水井单层累积注水倍数的计算方法[J].大庆石油学院学报,2005,29(2):28-30. Wu Jiawen,Song Kaoping,Wang Yimin,et al.Computing method of cumulative water injection multiple for water injection well in individual layer[J].Journal of Daqing Petroleum Institute,2005 ,29(2):28-30
[4] 朱义东.岔河集油田单井配注方法研究[D].南充:西南石油学院,2005
[5] 李凤琴,刘丽琼,丁全胜,等.分层累计吸水量劈分方法研究[J].河南石油,2005,19(5):28-29,32. Li Fengqin,Liu Liqiong,Ding Quansheng,et al.A study on calculation of accumulative water-intake rate of separate layer[J].Henan Petroleum,2005,19(5):28-29,32
[6] VAPNIK V N.Statistical learning theory[M].New York:Wiley,1998
[7] 王春林,周昊,李国能,等.基于遗传算法和支持向量机的低 NOx燃烧优化[J].中国电机工程学报,2007,27(11):40-44. Wang Chunlin,Zhou Hao,Li Guoneng,et al.Support vector machine and genetic algorithms to optimize combustion for low NOxemission[J].Proceedings of the CSEE,2007,27(11):40-44
[8] EBERHART R C,KENNEDY J.A new optimizer using particle swarm theory[R].Proceedings of the 6th international symposium on micro machine and human science.1995:39-43
[9] DING Shuaiwei,JIANG Hanqiao,LI Junjian,et al.Optimization of well placement by combination of a modified particle swarm optimization algorithm and quality map method[J].Computational Geosciences,2014,18(5):747-762
[10] 陈果.基于遗传算法的支持向量机分类器模型参数优化[J].机械科学与技术,2007,26(3):347-350. Chen Guo.Optimizing the parameters of support vector machine’s classifier model based on genetic algorithm[J].Mechanical Science and Technology,2007,26(3):347-350
[11] 张红梅,卫志农,龚灯才,等.基于粒子群支持向量机的短期电力负荷预测[J].继电器,2006,34(3):28-31. Zhang Hongmei,Wei Zhinong,Gong Dengcai,et al.A short-term load forecasting approach based on PSO support vector machine[J].Relay,2006,34(3):28-31
[12] 费胜巍,苗玉彬,刘成良,等.基于粒子群优化支持向量机的变压器故障诊断[J].高电压技术,2009 (3):509-513. Fei Shengwei,Miao Yubin,Liu Chengliang,et al.Fault diagnosis of transformer based on particle swarm optimization-based support vector machine[J].High Voltage Engineering,2009 (3):509-513. 收稿日期:2015-11-09 改回日期:2016-01-17
(编辑:杨 滨)
Prediction of water injection profile based on particle swarm optimization-support vector machine
Li Junjian1Zhou Daiyu2Zhao Ji2Ding Shuaiwei1Jiang Hanqiao1Zhang Shuzhen2Liang Bin1Kuang Xiyu2Wang Qian2
(1.KeyLaboratoryforPetroleumEngineeringoftheMinistryofEducation,ChinaUniversityofPetroleum,Beijing102249,China;2.ResearchInstituteofExplorationandDevelopment,TarimOilfieldCompany,PetroChina,Korla,Xinjiang841000,China)
The prediction of water injection profile is important for guiding the adjustment scheme of layered water injection and determination of water flooding status. Historical injection profile is the most accurate material to calculate the layered water absorbing capacity, but it is not used comprehensively because of the rare material or too simple interpolation method. In this paper, based on historical injection profile data, the injection profile prediction model is established through the regression fitting history injection profile data based on particle swarm optimization-support vector machine method (PSO-SVM), thus the prediction of injection profile without data is realized. The application results show the proposed method is accurate and reliable, which can provide the foundation for the division of injected-water volume for water injected well.
water injection profile prediction; support vector machine; particle swarm algorithm; regression forecasting model
*国家青年自然科学基金“复杂裂缝潜山油藏水平井堵水封堵机理研究(编号: 51404280)”部分研究成果。
李俊键,男,副教授,2010年毕业于中国石油大学(北京)油气田开发工程,获博士学位。地址:北京市昌平区府学路18号(邮编:102249)。E-mail:junjian@126.com。
1673-1506(2016)05-0066-05
10.11935/j.issn.1673-1506.2016.05.011
TE319
A
