基于DAPSO-UGM(1,1)模型的物流需求预测
2016-06-23张连伟耿立艳
张连伟,何 梁,耿立艳
(石家庄铁道大学 经济管理学院,河北 石家庄 050043)
基于DAPSO-UGM(1,1)模型的物流需求预测
张连伟,何梁,耿立艳
(石家庄铁道大学经济管理学院,河北石家庄050043)
[摘要]物流需求预测的准确性对我国的经济发展具有重要作用。为提高物流需求的预测精度,文章利用动态自适应粒子群优化算法(DAPSO)优化无偏灰色预测模型[UGM(1,1)]参数,构建DAPSO-UGM(1,1)模型预测物流需求。以我国物流需求为例,证明了DAPSO-UGM(1,1)模型的有效性,并预测了未来我国的物流需求,为物流需求预测提供了新的方法。
[关键词]动态自适应粒子群算法;无偏灰色预测模型;物流需求预测
[DOI]10.13939/j.cnki.zgsc.2016.10.010
随着经济的发展,物流需求在交通网络规划、物流设施投资和物流规划等方面扮演着越来越重要的角色,因此准确的物流需求预测对我国的经济发展具有重要的意义。现有的预测模型中较为常用的是时间序列、回归分析和灰色预测模型,由于时间序列和回归分析预测模型在实际应用中考虑的相关因素较少,因此预测误差相对较大,而灰色预测模型在预测时需要的数据较少,预测精度较高且适用于中长期的预测,所以不少学者开始将灰色预测(GM(1,1))模型引入物流需求预测[1,2]中,而在物流需求预测中GM(1,1)模型[3]是最常用的。在GM(1,1)模型的基础上,又出现了预测性能优于GM(1,1)模型的无偏灰色预测(UGM(1,1))模型[4],但该模型随着发展系数的变大,性能有变差的趋势,进而导致物流需求的预测精度下降。粒子群优化(PSO)算法是一种群智能优化算法[5],在参数优化方面得到广泛应用。作为PSO算法的改进算法,动态自适应粒子群优化(DAPSO)算法[6]根据粒子早熟收敛程度和个体适应度值动态地调整惯性权重,提高了算法的收敛速度和精度。本文利用DAPSO算法优化UGM(1,1)模型的参数,以进一步提高物流需求预测的精度。
1无偏灰色预测模型
GM(1,1)模型是以“部分信息已知,部分信息未知”的“小样本”“贫信息”的不确定性系统为研究对象,由已知的部分信息预测未知信息的一种模型。而无偏灰色预测(UGM(1,1))模型则对GM(1,1)模型做了进一步改进,消除了传统GM(1,1)模型存在的固有偏差。UGM(1,1)模型的建模步骤如下:
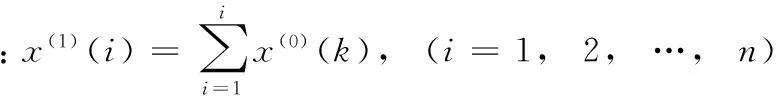
(1)
其中,a为发展灰度,u为内生控制灰度。通过最小二乘法求解参数列C=[au]T:
(2)
其中,B和Yn分别为:
(3)
建立原始数据序列模型:
(4)
(5)
2动态自适应粒子群优化算法
PSO算法是最近几年内出现的迭代优化算法,首先给定一组初始值,然后根据已知函数确定适应值(fitness value)并且不断地进行迭代优化,即模拟粒子在空间内按照一定的约束,进行相应的搜索,从而使得粒子找到本身的最优值,包括个体极值(pbest)和群体极值(gbest)。
设在D维空间中存在一个群体,该群体中包含n个粒子,第i个粒子的位置为Xi=(xi1,xi2, …,xiD); 速度为Vi=(vi1,vi2, …,viD); 当前搜索到的最优位置为Pi=(pi1,pi2, …,piD), 在群体中搜索得到的最优位置为Pg=(pg1,pg2, …,pgD)。将以上的各个量带入目标函数,可以计算出函数的适应值,得到粒子状态的更新公式为:
Vid=WVid+c1r1(Pid-Xid)+c2r2(Pid-Xid)
(6)
Xid=Xid+Vid
(7)
其中,i=1,2,…,s,d=1,2,…,D;W为惯性权重,c1、c2为学习因子,r1、r2是[0,1]的随机数。式(6)中,反映了粒子先前速度的惯性大小,当W值较大时,全局搜索能力强,收敛速度快;当W值较小时,局部搜索能力强,解的精度高,收敛速度慢。所以,在一般的PSO算法中,W的值通常在0.1~0.9,为了使惯性权重对算法能否收敛更加准确,可采用一种基于群体早熟收敛程度和个体适应值来调整惯性权重的动态自适应粒子群算法。
2.1算法早熟收敛度评价
设粒子i的当前适应值为fi,当前适应值的平均值为favg,则有以下计算式:
(8)
(9)
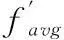
2.2自适应调整策略
PSO算法中,当搜索出现局部极值时,粒子停滞;当粒子群在局部极值附近运动较小时,根据其早熟收敛程度,可对W做动态自适应调整,调整方法为:
(1)fi比favg好。
(10)
(2)fi比favg好,但搜索效率差。
(11)
其中,Wmax为最大惯性权重,Wmin为最小惯性权重,m、Wmax分别为当前迭代次数和最大迭代次数。
(3)fi比favg差。
(12)
其中,参数k1主要影响算法的最大惯性权重,参数k2主要影响惯性权重的调节能力。
3DAPSO-UGM(1,1)模型
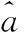
(13)
第二步:确定目标函数。以模型预测值与实际物流需求的误差的平方和最小为目标函数。
(14)
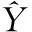
第三步:初始化每个粒子的位置和速度。
第四步:评价每个粒子的适应值。
第五步:得到每个粒子的pbest和gbest。
第六步:利用式(6)和式(7)更新各个粒子的位置和速度。
第七步:如果达到精度要求或者达到最大的迭代次数,输出gbest及其适应值并停止迭代,否则返回第四步。
4模型应用
4.1数据选取
以货运量作为物流需求的量化指标,选取2006—2013年我国货运量数据,检验DAPSO-UGM(1,1)模型的预测效果。所用数据来源于《中国统计年鉴2014》。表1给出2006—2013年我国货运量数据。由表1可知,我国2006—2013年货运量基本呈指数增长趋势,因而采用DAPSO-UGM(1,1)模型进行分析和预测是合理的。
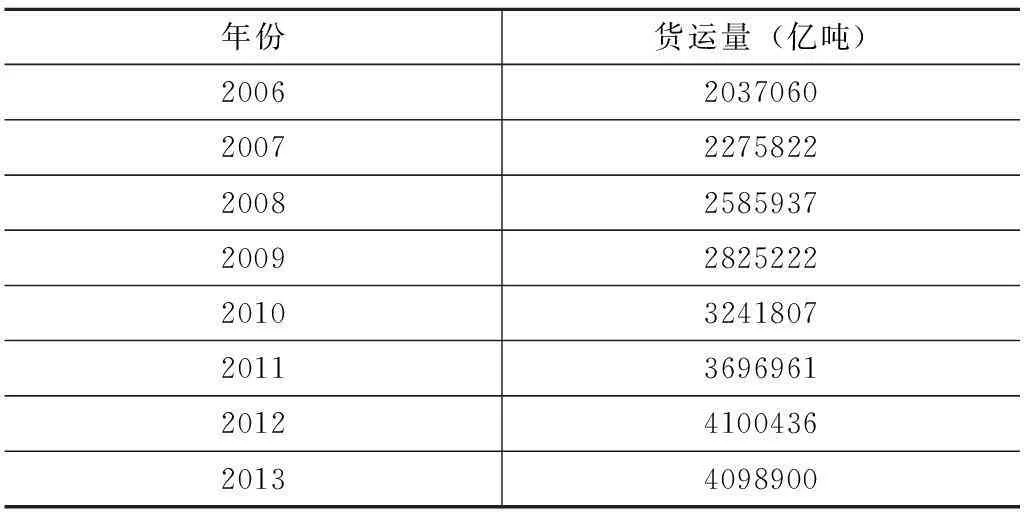
表1 2006—2013年物流需求
4.2模型检验
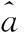
由表2可知,DAPSO-UGM(1,1)模型的最大、最小相对误差为3.39%和0.02%,分别小于GM(1,1)模型、UGM(1,1)模型和PSO-UGM(1,1)模型的对应值,同时其平均相对误差也明显小于其他三模型,这有力证明了DAPSO-UGM(1,1)模型的预测精度优于其他三模型。因此,基于DAPSO算法优化的UGM(1,1)是一种有效的物流需求预测方法。
4.3外推预测
将DAPSO-UGM(1,1)模型应用于未来物流需求预测中,利用DAPSO-UGM(1,1)模型预测2014—2020年的物流需求,预测结果如表3所示。从表3可以看出,未来7年物流需求将呈现出先增后减的变化趋势。
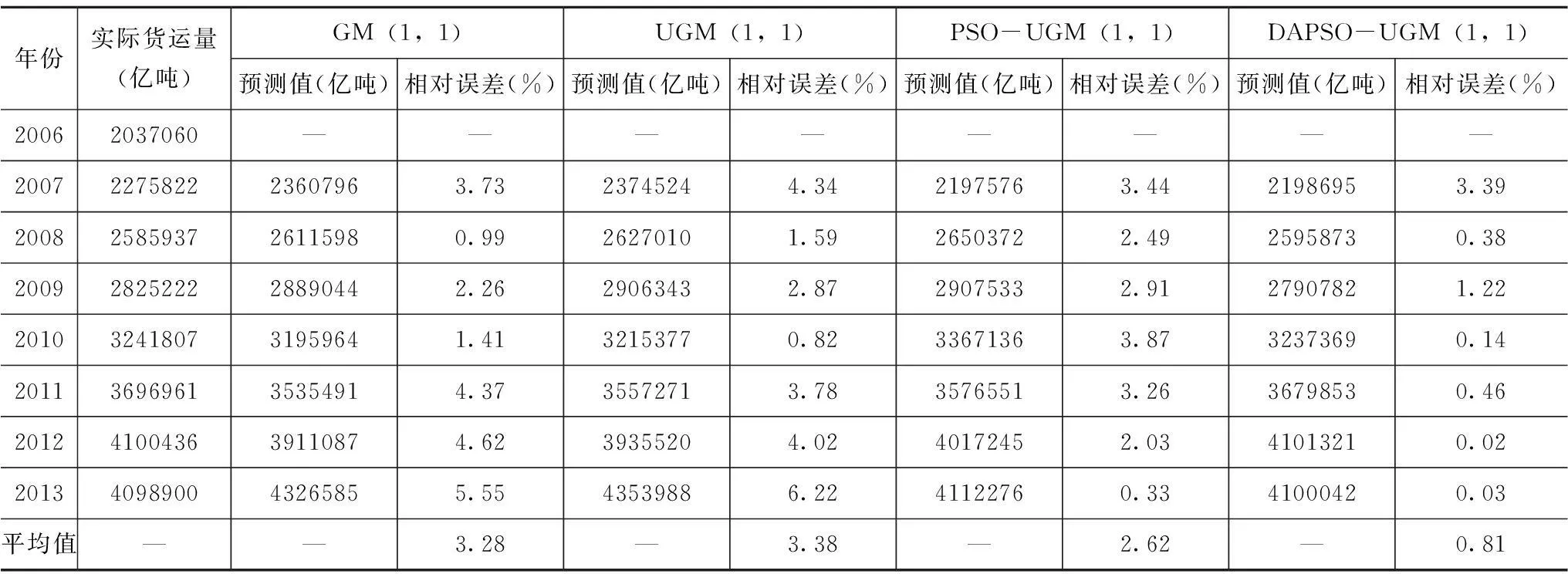
表2 检验结果比较
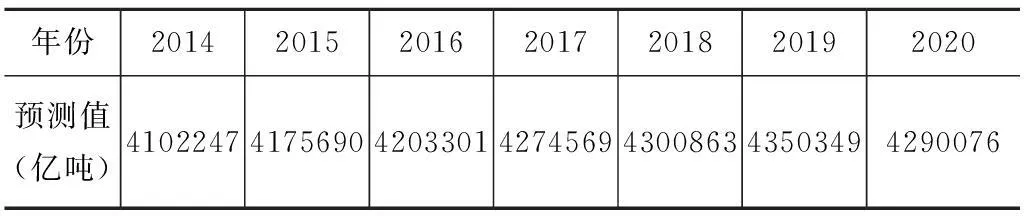
表3 2014—2020年物流需求
5结论
本文结合DAPSO算法与UGM(1,1)模型,构建DAPSO-UGM(1,1)物流需求预测模型,利用DAPSO算法优化UGM(1,1)模型参数。通过对我国物流需求的实例分析,验证了DAPSO-UGM(1,1)模型是一种有效的物流需求预测方法,并利用该模型预测了未来我国的物流需求。
参考文献:
[1]张潜.物流需求回收预测及其实证分析[J].哈尔滨工业大学学报:社会科学版,2010,12(1): 84-89.
[2]王小丽.基于多因素灰色模型的物流需求量预测[J].统计与决策,2013(14): 86-87.
[3]刘思峰.灰色系统理论及其应用[M].北京:科学出版社,2014.
[4]刘鹄,吉培莱,邹红波.无偏灰色预测模型在边坡变形预测中的应用[J].三峡大学学报:自然科学版,2007,29(1): 43-45.
[5]张芳芳,王建军,张勇.少控参数的分层式骨干粒子群优化算法[J].系统工程理论与实践,2015,35(12): 3217-3224.
[6]盛桂敏,薛玉翠,张博阳.动态自适应粒子群优化算法[J].绥化学院学报,2011,31(6): 190-192.
[基金项目]2015年度大学生创新创业训练计划项目“物流需求的智能预测方法及实证研究”;国家自然科学基金青年项目(项目编号:61503261);河北省软科学研究计划项目(项目编号:15456106D);河北省社会科学发展重点研究课题(项目编号:2015020206)。
