Cayley-Hamilton定理的几种证法

张华民，殷红彩,梅　红

Cayley-Hamilton定理的几种证法

张华民，殷红彩,梅红

摘要:通过Krylov子空间、Schur定理和数学归纳法等方法，给出了Cayley-Hamilton定理的三种证法。

关键词:Krylov子空间; Cayley-Hamilton定理; Schur定理

1Cayley-Hamilton定理

Cayley-Hamilton定理是用英国数学家Arthur Cayley(1821-1895)和爱尔兰数学家William Rowan Hamilton(1805-1865)的名字命名的一个定理[1]，同时也是线性代数中的一个重要定理，该定理在矩阵的逆和广义逆的计算、矩阵幂的计算和矩阵指数函数的计算中有重要的应用[2]。下面先给出这个定理。考虑一元多项式方程根的情况，本文的讨论在复数域上展开。

设复数域C上的方阵为A,即有A∈Cn×n,该矩阵的特征多项式f(λ)定义为

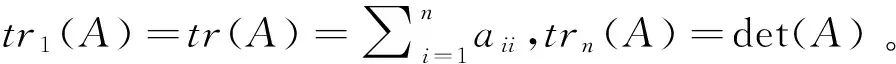
Cayley-Hamilton定理实数域R上的每个方阵A都满足它的特征方程，即有

其中O为n阶零方阵。

2Cayley-Hamilton定理的几种证法

Cayley-Hamilton定理有多种证法，但下面参考文献[3]的证法并不常见。这种证法是受Krylov子空间的启发。该方法并不要求明确知道矩阵A,只要知道向量Au的产生机制就行了。先给出如何用这种方法来确定矩阵A的特征多项式。

任取u∈Cn,此处不妨设u=(1,0,0,…,0)T,计算向量序列Au,A2u,…,每计算下一个向量前先判别向量组u,Au,A2u,…,的线性相关性.不失一般性，假设向量组u,Au,A2u,…,Ar-1u线性无关，而向量组u,Au,A2u,…,Ar-1u,Aru线性相关。在下面的等式中设向量Aru的系数为1，即有

b0u+b1Au+b2A2u+…+br-1Ar-1u+Aru=0.

注意到在复数范围内，实系数多项式总可以分解成一次因式的乘积，即上式可写为

上式的每一种记法均表示矩阵A的一个特征值和对应的特征向量，即均表示一个特征对，例如上式第二个等号右端的式子表示(A-λ2I)…(A-λrI)u是特征值λ1的特征向量。

注意到n+1个n维向量必线性相关，故如果r=n,则可得矩阵A的特征多项式为

若r

线性无关，而向量组

u,Au,A2u,…,Ar-1u,v,Av,A2v,…,As-1v,Asv

线性相关，即有下面的线性组合

(1)

将(1)式两边同时左乘以矩阵b0I+b1A+b2A2+…+br-1Ar-1+Ar,并注意到相关矩阵乘法的可交换性得到

若r+s=n,则可得矩阵A的特征多项式为

若r+s

由此可得Cayley-Hamilton定理的一种证法。

证法一由上面矩阵A的特征多项式f(λ)的给出过程可得，对任意的u∈Cn始终有f(A)u=0,当u取遍单位矩阵I的每一列就可得到f(A)=O,证毕。

下面的证法用到了矩阵的Schur分解定理和数学归纳法[4-6]。

证法二由矩阵的Schur分解定理，矩阵A相似于上三角矩阵，即存在可逆矩阵P使得

其中λ1,λ2,…,λn是矩阵A的n个特征值，显然有

注意到f(A)=Pf(T)P-1,且矩阵P可逆，故只需证明f(T)=O即可。对n用数学归纳法，当n=1时命题显然成立。下面设n≥2,并设命题对n-1阶方阵已成立, 令

则块矩阵T22的特征多项式为

由归纳假设有g(T22)=On-1,由f(λ)=(λ-λ1)g(λ)可知

于是

证毕。

下面证法在不少文献中出现[2,7,8]，将它列出作为一种证法。

证法三因为矩阵λI-A的伴随矩阵adj(λI-A)是由矩阵λI-A的代数余子式为元素构成的矩阵，故伴随矩阵adj(λI-A)是关于的λ次数不超过n-1的多项式矩阵，即有

其中B0,B1,…,Bn-1∈Rn×n。 由关系式

(λI-A)adj(λI-A)=det(λI-A)I=f(λ)I

可得

(λI-A)adj(λI-A)

(2)

和

(3)

比较上面(2), (3)两式λ的相同次幂对应的系数矩阵可得

(4)

将(4)式中的前n个等式分别左乘矩阵An,An-1,…,A. 然后再将这n+1个等式相加即得

这正是所要的结果。证毕。

由这种证法还可得到一些很有意思的结论，列在下面。

注1关于矩阵A的特征矩阵λI-A的伴随矩阵adj(λI-A)有下面的结论。

矩阵A的特征多项式的定义如上，则矩阵λI-A的伴随矩阵的展式可写为

(5)

事实上，由上面证明过程的(4)式可得

将(4)式代入(3)化简合并即得(5)式。

注2由上面的证明过程可以发现，等式(5)可写为

且矩阵A与B1,B2,…,Bn-1间的乘法是可交换的。

3结束语

本文介绍了Cayley-Hamilton定理的三种证法，后面两种证法在一些文献中很常见，第一种证法借助于用Krylov子空间产生矩阵的特征多项式的性质获得启发，证明过程简单明了。文献[9]借助Vandermonde行列式也给出了该定理的证明，文献[10]利用了矩阵的初等运算给出了该定理的一种证明。Cayley-Hamilton定理在矩阵求逆、矩阵幂和矩阵指数函数等方面有重要的应用[2,11]。该定理还可作进一步的推广[12]，能否利用Krylov子空间的方法证明Cayley-Hamilton定理的一些推广形式有待进一步的研究。

[参考文献]

[1]李文林. 数学史概论(第三版) [M]. 北京: 高等教育出版社, 2011:213-215.

[2]张贤达. 矩阵分析与应用[M]. 北京: 清华大学出版社, 2004: 474-484.

[3]S.K. Jain, A.D. Gunawardena. Linear Algebra: An Interative Approach[M]. NewYork: Thomson Learnig, 2004: 159-161.

[4]王卿文. 线性代数核心思想及应用[M]. 北京：科学出版社, 2012: 63-63.

[5]R.A. Horn, C.R. Johnsom. Matrix Analysis[M]. Cambridge : Cambridge University Press, 1999: 86-87.

[6]刘国新, 王正攀. Cayley-Hamilto定理的一个新证明[J]. 西南师范大学学报(自然科学版): 2013, (8): 1-2.

[7]王萼芳, 石生明修订. 高等代数[M]. 第三版.北京:高等教育出版社, 2007: 83-86.

[8]戴华. 矩阵论[M]. 北京: 科学出版社, 2001: 110-111.

[9]杨艳, 刘合国. Cayley-Hamilton定理的一个证明[J]. 数学的实践与认识: 2009, (9): 235-238.

[10]杨艳, 刘合国. Cayley-Hamilton定理的有理证明[J]. 湖北大学学报(自然科学版) : 2009,(2):109-112.

[11]戴中林. Cayley-Hamilton定理的应用[J]. 四川师范学院学报(自然科学版): 1999, (4): 391-393.

[12]李师正. Cayley-Hamilton定理的推广[J]. 曲阜师范大学学报(自然科学版): 1991, (4): 13-14.

责任编辑：王与

Several Proofs of the Cayley-Hamilton Theorem

Zhang Huamin，Yin Hongcai, Mei Hong

Abstract:By using the Krylov subspace, Schur Theorem and the mathematical induction, three proofs of the Cayley-Hamilton Theorem are presented.

Key words:Krylov subspace; Cayley-Hamilton Theorem; Schur Theorem

中图分类号：O151.2

文献标识码：A

文章编号：1673-1794(2016)02-0013-03

作者简介：张华民，蚌埠学院数理系副教授，博士；殷红彩，安徽财经大学管理科学与工程学院；梅红，蚌埠学院数理系(安徽 蚌埠 233000)。

基金项目：安徽省教育厅重点项目(KJ2016A458)；安徽财经大学自然科学基金资助(ACKY1654)；2013教学团队(jxtd02)；2014省级质量工程(2014zy141)；蚌埠学院院级项目 (2011ZR17,2015ZR10);安徽省省级教研项目(2015jyxm386)

收稿日期：2015-11-12