极化SAR图像K分布模型参数估计方法研究与仿真

晏庆,崔浩贵,易帆帆

(1.91469部队,北京 100841;2.海军工程大学 电子工程学院,武汉 430033)

极化SAR图像K分布模型参数估计方法研究与仿真

晏庆1,崔浩贵1,易帆帆2

(1.91469部队,北京 100841;2.海军工程大学 电子工程学院,武汉 430033)

摘要：极化合成孔径雷达(SAR)已成为一种不可或缺的地理遥感和军事侦察信息源,但是其图像解译困难,需要借助精确的建模方法与分析手段。K分布模型是常用的极化SAR图像模型,但是传统参数估计方法准确性较差的问题影响了模型的拟合精度．针对该问题,首先推导了K分布矩阵行列式值的概率密度函数及其最大似然(ML)估计方法,并用仿真数据验证了其有效性，然后将ML估计方法应用于K分布模型的等效视图数(ENL)估计中,比较了其与传统的方法在ENL估计上的性能差异。仿真和实测数据的实验结果均表明，新方法具有更小的估计偏差和方差,对解决极化SAR图像中K分布区域的参数准确估计问题有重要的实用价值。

关键词：K分布;雷达图像;最大似然估计;协方差矩阵

0引言

极化合成孔径雷达(SAR)具有全天时、全天候的多维信息遥感能力和不同目标极化特性的鉴别能力,但是相干成像技术都固有的相干斑增加了极化SAR图像解译的难度。为了从极化SAR图像中提取出有用的信息,建立精确的相干斑模型并进行准确的数学分析是非常有效的手段。传统的相干斑建模方法是假设散射回波服从高斯分布[1]。

但是随着雷达分辨率的提高,需要借助非高斯模型来刻画回波的特性。在极化SAR图像非高斯建模领域中,最常用的是基于乘积模型推导得到的K分布[2]，该模型将协方差矩阵表示为服从伽马分布的纹理变量与服从Wishart分布的相干斑变量的乘积。

参数估计的准确性很大程度上决定了极化SAR图像K分布模型的拟合精度。最常用的矩阵估计方法存在表达式非常复杂并且估计精度不高的问题[3]。Anfinsen等将Mellin变换应用到了K分布的参数估计中,提出了基于一阶对数累积量的等效视图数(ENL)估计方法[3-5]。但是该方法在预先估计矩阵行列式值时采用了先求协方差矩阵样本的均值,再取其行列式值的方法，这实际上是一种有偏估计方法,导致ENL的估计性能较差[6]。

本文推导了K分布矩阵行列式值的分布和其最大似然(ML)估计方法,用查表法解决了ML估计方法计算复杂度高的问题。仿真结果表明,相比传统的估计方法,本文方法具有更小的偏差和方差。新方法为ENL这一关键参数的准确估计提供了新的途径,对后续的PolSAR图像相干斑滤波和检测等领域的应用有着重要意义。

1极化SAR图像协方差矩阵建模

1.1极化SAR图像特性

极化SAR是一种主动式的微波成像设备,具有分辨率不受雷达传感器高度影响的优点,其雷达信号能穿透云层。另外,波长较长的L波段信号能穿透森林和地表植被覆盖,在军事上能够用于发现丛林中的隐藏目标和获取地表以下的信息,这些是光学等其它传感器无法实现的。

最常见的极化SAR为机载形式,美国NASA的JPL实验室研制的AIRSAR系统可以在P、L和C三个波段上进行全极化测量成像。该系统自首飞后每年至少执行一次测量任务,成为验证新开发雷达技术的主要实测数据来源。AIRSAR系统安装于DC-8飞机的底部,如图1所示。

图1　AIRSAR系统

Pauli分解是将目标的散射矩阵表示为各Pauli矩阵的加权和,其中每个Pauli矩阵都对应着一种特定的散射机制。在得到Pauli分解的RGB合成图时往往只用其中三种散射机制进行合成,分别为奇次散射、偶次散射和体散射。其中奇次反射一般发生在平面上,例如海洋或者光秃的地面;偶次散射经常发生于城区;体散射常见于植被区域。在进行合成时这三种散射机制分别用蓝色、红色和绿色来表示,其加权值代表颜色的深度。

图2示出了Flevoland地区和San Francisco海湾地区极化SAR图像的Pauli分解RGB合成图。这两幅图像都是由AIRSAR系统获取的,其图像大小分别为750×1024和900×1024,是常用的极化SAR实测数据。

图2　极化SAR图像RGB合成图Pauli分解　　　(a)Flevoland； (b)San Francisco

1.2极化SAR图像K分布建模

为了解译如图2所示的极化SAR图像,首先要对其进行建模。常用的非高斯建模方法是乘积模型,在该模型假设下,极化SAR图像的协方差矩阵C可表示为

C=τY,

(1)

式中: τ为纹理变量; Y为相干斑变量,并且纹理变量和相干斑变量相互统计独立。一般认为相干斑变量Y服从Wishart分布,其PDF为[5]

(2)

式中:L为视图数;d表示矩阵的维数;Γ为方差矩阵; Tr(·)表示取矩阵的迹;Γd(L)为多变量伽马函数

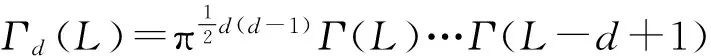
(3)

式中,Γ(L)为标准欧拉函数。

当纹理变量τ满足伽马分布时,根据式(1)所示的乘积模型,可以得到极化SAR图像的协方差矩阵服从K分布。一般假设纹理变量满足单位均值的条件,归一化伽马分布的概率密度函数(PDF)为

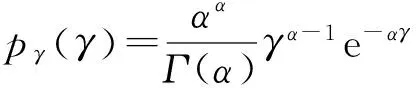
(4)

式中,α为伽马分布的形状参数。

根据式(1)、式(2)和式(4),可以得到K分布的PDF为

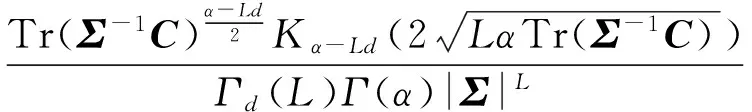
(5)

式中,Σ=E(C);Kα-Ld(·)为第α-Ld阶的第二类修正Bessel函数。

2K分布矩阵行列式值的最大似然估计

特征函数(CF)是研究随机变量PDF的一个重要工具,有些随机变量要确定其分布可能比较困难,但是确定其特征函数却比较简单。平常所指的特征函数实际上是随机变量PDF的逆Fourier变换。文献[7]中Nicolas提出了用Mellin变换代替Fourier变换来分析随机变量的分布,对于随机变量X∈R+,定义其基于Mellin变换的特征函数(MCF)为[8]

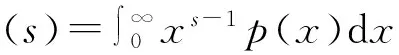
(6)

式中,p(x)为随机变量X的PDF,对应的逆变换为

p(x)=M-1{φX(s)}(x)

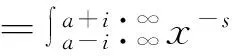
(7)

对式(1)所示的乘积模型进行Mellin变换,可得其MCF存在如下关系:

φC(s)=φτ(s)·φY(s).

(8)

由于x=(2L)d|C|/|Σ|服从d个χ2分布的乘积[9],可得其Mellin变换为

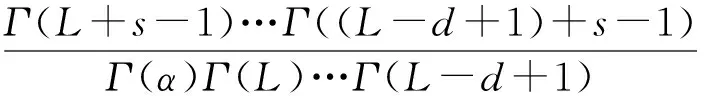
(9)

利用式(7)的定义对式(9)进行Mellin逆变换,令Υ=|C|,可以求出协方差矩阵行列式值分布的PDF

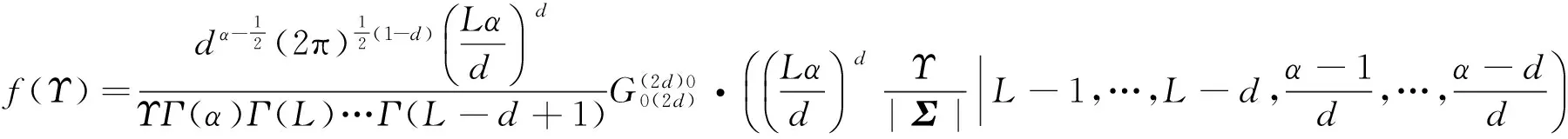
(10)

式中MeijerG函数的定义为

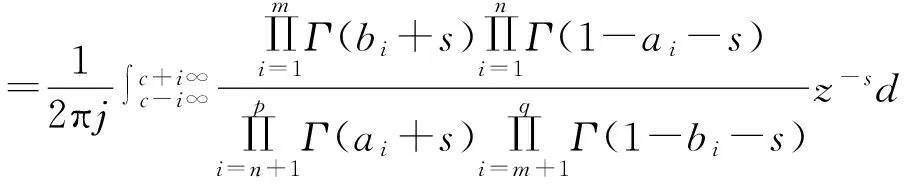
(11)

那么其最大似然估计可由对数似然比公式求取

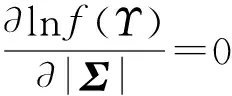
(12)

求得

(13)

其中参数z为下式的解

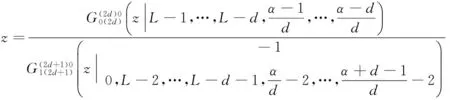
(14)

3仿真实验分析

3.1K分布矩阵行列式值ML估计的性能分析

在实际中利用式(13)对行列式值进行最大似然估计时,需要首先求解式(14)。可以看到一方面式(14)没有解析的表达式,需要用搜索的方法求解。另一方面,该式中包含复杂的MeijerG函数。如在用样本数据对行列式值进行估计的过程中实时求解式(14)的话会碰到计算复杂度较大的问题,这降低了算法的实用性。这里采用查表法来解决ML方法计算复杂的问题。注意到式(13)中的d实际上为常数,即d=3.令

f(L;α)=(Lα/d)d，

(15)

则式(13)可表示为

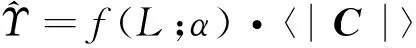
(16)

其中f(L;α)定义为行列式值最大似然修正系数。

在进行参数估计之前,首先仿真得到二维表格形式的最大似然修正系数f(L;α)。由于α等于200时,K分布已经近似于高斯情形,而L要求大于d.因此在建表时,参数选择的范围为α∈(0,200],L∈(3,1000]。图3示出了K分布的形状参数α分别为2,4,200时,仿真得到的最大似然修正系数关于L的变化曲线。从图中可以看出,随着L的增加,最大似然修正系数趋向于一个固定值。其次,可以看出不同形状参数下的修正系数只有在L较小时有稍微差别,随着L的增加该差别基本可以忽略。另外,可以看到当L<4时,最大似然修正系数的变量速率较快,此时应在建表时应采用较小的间隔。因此在实际应用中预先建立的是一个非均匀间隔索引的表:当L≤4时,以间隔值ΔL=0.01建表;当L>4时,以ΔL=0.1建表。

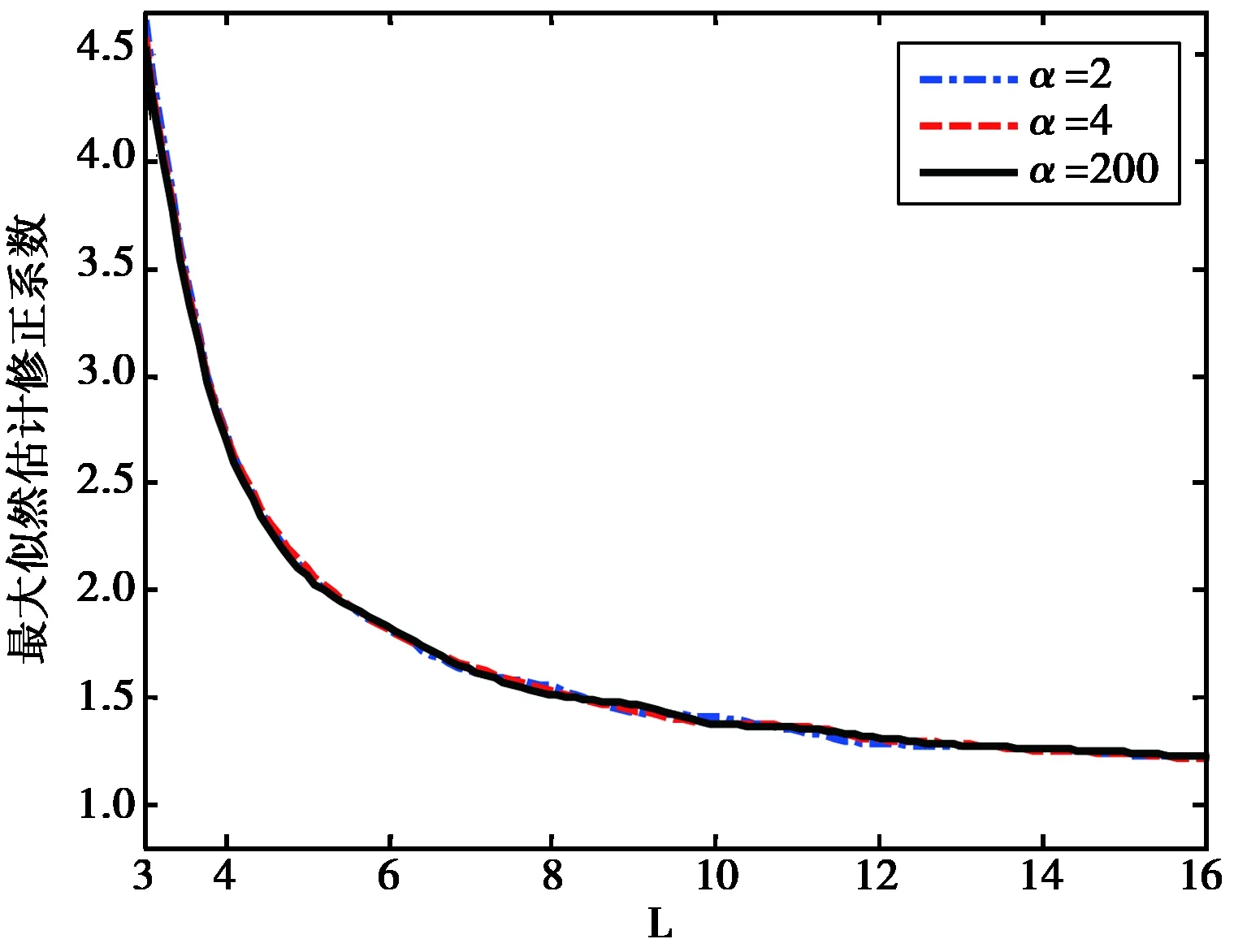
图3　最大似然修正系数仿真图

为了验证本文提出的估计方法的有效性,这里用K分布的仿真数据将本文方法与传统的基于协方差矩阵均值的行列式值的估计方法(即|Σ|=|E{C}|)的结果进行仿真比较。K分布的仿真数据采用Bootstrap的方法由式 (1)所示的乘积模型仿真得到。为了突出显示数据分布图的峰值,这里引入了一种基于核密度估计KDE的非参数估计方法[4]。其中h称为带宽,它决定图像的平滑程度,在此采用Epanechnikov核函数。带宽h的选择对峰值的幅度有较大影响,但是对峰值的位置影响不大,本文选取带宽h=0.3.

图4示出了K分布仿真数据下,取不同的形状参数时,传统的基于均值的行列式值估计方法和本文提出的ML估计方法的估计偏差和方差。这里仿真数据服从L=4,|Σ|=1的K分布,仿真次数M=10000．图中的横轴为样本数,图4(a)的形状参数为α=8,图4(b)为α=2．从图中首先可以看出随着样本数的增加,估计偏差和方差都在减小。其次,可以看出相比传统的方法,本文方法具有更小的估计偏差和方差,其性能更优。另外,对比图4(a)和图4(b),可以看出当形状参数较大时,参数估计的偏差和方差相对较小，这是因为随着形状参数的增大,K分布数据会变均匀,并趋向于高斯情形。而形状参数较小时,K分布的数据比较奇异,导致参数估计性能变差。

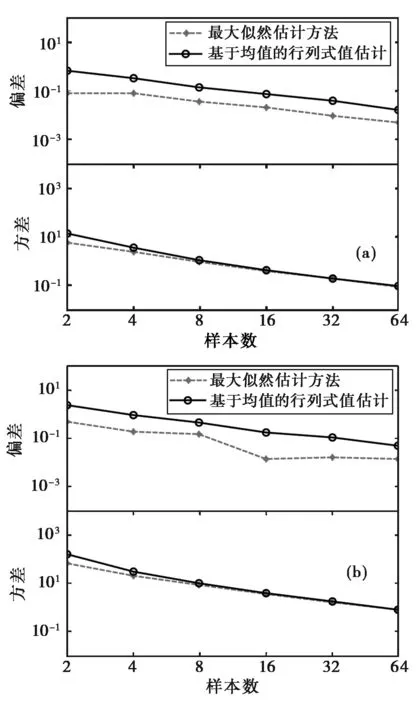
图4　不同算法下K分布矩阵行列式值的估计偏差与方差 (a) α=8 ; (b) α=2

3.2矩阵行列式值ML估计方法在极化SAR图像ENL估计中的应用

ENL是极化SAR图像中的一个重要参数,它表征了参与多视的样本的数目,一般采用基于一阶对数累积量的方法进行估计[3]

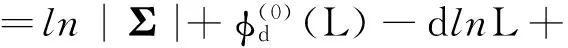
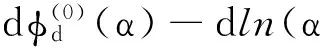
(17)

这里不详细讨论α的估计,用基于二阶矩特征的方法预先估计[3],并在处理过程中将其视为已知。

由于传统的基于矩阵均值的行列式值的估计方法是有偏估计,为了提高ENL估计的准确性,我们可以联合式(13)与式(17)来估计ENL。首先用名义视图数代入式(13),估计出|Σ|;然后将|Σ|的估计值代入式(17)估计出ENL。该方法的步骤可总结如下:

1) 根据式(13)和(14),用数值仿真方法计算出最大似然修正系数;

2) 预先建立的是一个非均匀间隔索引的表,即L和α关于f(L;α)的二维索引表:当L≤4时,以间隔值ΔL=0.01建表;当L>4时,以ΔL=0.1建表;

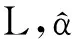
图5示出了仿真数据情形下,分别用本文ML方法和传统的基于均值的方法估计出行列式值后,由一阶对数累积量方法估计得到的ENL结果。其中仿真数据服从参数为L=4,|Σ|=1的K分布,仿真次数为M=10000.图5(a)的形状参数为α=8,图5(b)为α=2.从图5可以看出随着样本数的增加,两种方法的估计偏差和方差之间的差异在减小，其次,本文的ML估计方法在对K分布矩阵的行列式值进行修正后,相比原有算法能有效改善ENL的估计精度。最后,对比图5(a)和图5(b)可以看到当形状参数较大时,ENL估计结果的偏差和方差都相对较小。

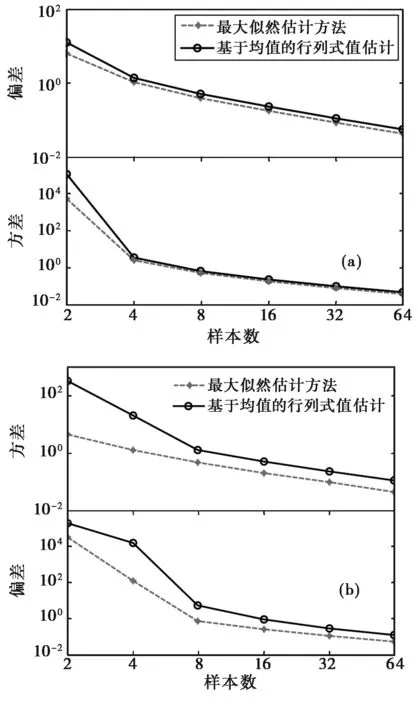
图5　不同算法下L的估计偏差与方差(a) α=8; (b) α=2

3.3实测数据仿真分析

用图2所示的实测数据来对两种ENL估计方法进行仿真分析。首先从图2(a)中可以看出,Flevoland图像中大部分区域为农田和植被等符合K分布的数据,右上角的河流可认为服从形状参数较大的K分布。其次从图2(b)可以看出,SanFrancisco主要由海洋、城区和植被3个部分构成。其中,植被区域一般认为服从K分布。城区较为奇异,可能满足形状参数较小的K分布。而海洋接近高斯分布,可认为是形状参数较大的K分布。

这里用无监督的滑窗估计方法来对实测数据的ENL值进行估计[4]。该方法首先用k×k的滑动窗口将整个图像分解成很多个小区域,然后根据每个区域中的样本数据计算出其对应的ENL值,最后对所有区域的ENL估计结果进行统计。由于上述两幅极化SAR图像中的大部分区域都可以用K分布来进行建模,这里取ENL统计分布图的峰值作为整个图像的ENL值。

图6示出了实测数据下本文给出的ML估计方法和传统的估计方法在不同的滑窗值k下ENL的估计结果。其中滑窗值的大小分别选取为k={2,3,5,7,11}。对比不同窗口k下的结果可以看出,当窗口值较小时本文方法的优势比较明显,但是随着窗口值的增大两种方法的差别在减小。该结论也与图3和图4中通过仿真数据得到的结果相符。另外,可以看到本文的ML估计方法的在不同窗口值下的表现比较稳定,而传统的方法在k较小时其分布的峰值出现偏差。

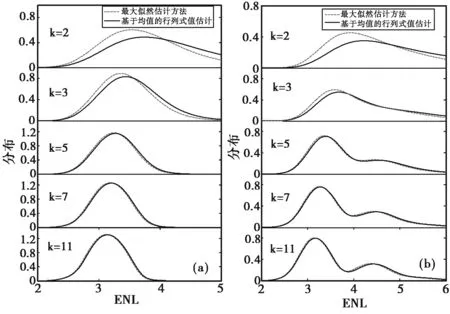
图6　实测数据下各估计方法对ENL的估计结果的比较(a) Flevoland; (b) San Francisco

4结束语

本文研究了在三维情形下,K分布矩阵的行列式值的统计分布特性,推导了其PDF和ML估计方法。针对ML估计方法的表达式计算复杂度高的问题,提出了先仿真出ML修正系数再进行查表的解决方法。仿真数据的实现表明,相比原有的基于矩阵均值的行列式值的估计方法,该方法的优势明显。然后,将矩阵行列式值的ML估计应用于极化SAR图像的基于一阶对数累积量的ENL估计方法中。最后用仿真数据和实测数据验证了该方法在对ENL估计的准确性和有效性,实现解决现实其估计效果改善明显。

但是,在用查表法获得最大似然修正系数的过程中,由于表的间隔以及数据位数的限制,会使估计结果存在一定的误差,该误差的影响还有待分析。另外,四维或者更多维情形K矩阵行列式值的PDF及其ML估计方法也有待后续的研究。

参考文献

[1]LEEJS,HOPPELKW,MANGOSA, et al.IntensityandphasestatisticsofmultilookpolarimetricandinterferometricSARimagery[J].IEEETransactionsonGeoscienceandRemoteSensing, 1994, 32(5):1017-1028.

[2]AKBARIV,DOULGERISAMOSERG, et al.ATextural-contextualmodelforunsupervisedsegmentationofmultipolarizationsyntheticapertureradarimages[J].IEEETransactionsonGeoscienceandRemoteSensing, 2013, 51(4):2442-2453.

[3]ANFINSENSN,ELTOFTT.Applicationofthematrix-variateMellintransformtoanalysisofpolarimetricradarimages[J].IEEETransactionsonGeoscienceandRemoteSensing, 2011, 49(6):2281-2295.

[4]ANFINSENSN,DOULGERISAP,ELTOFTT.Estimationoftheequivalentnumberoflooksinpolarimetricsyntheticapertureradarimagery[J].IEEETransactionsonGeoscienceandRemoteSensing, 2009, 47(11):3795-3809.

[5]ANFINSENSN,DOULGERISAP.OULGERISP,etal.Goodness-of-fittestsformultilookpolarimetricradardatabasedontheMellintransform[J].IEEETransactionsonGeoscienceandRemoteSensing, 2011, 49(7):2764-2781.

[6]刘涛, 崔浩贵, 高俊.Wishart分布矩阵行列式值的统计特性及其在参数估计中的应用[J]. 电子学报, 2013, 41(6):1231-1237.

[7]NICOLASJM.Introductiontosecondkindstatistics:applicationoflog-momentsandlog-cumulantstoSARimagelawanalysis[J].TraitementduSignal, 2002, 19(3):139-168.

[8]POULARIKASAD.Transformsandapplicationshandbook[D].CRCPress, 2010.

[9]GOODMANN.StatisticalanalysisbasedonacertainmultivariatecomplexGaussiandistribution(anintroduction)[J].theAnnalsofMathematicalStatistics, 1963, 34(1):152-177.

晏庆(1979-),男,湖南人,硕士， 主要研究方向为通信技术与计算机应用。

崔浩贵(1987-),男,浙江人,博士,研究方向为雷达极化信息处理、电子战建模与仿真。

ResearchandSimulationonParameterEstimationMethodofKDistributionforPolarimetricSARImagery

YANQing1,CUIHaogui1,YIFanfan2

(1.Unit 91469, Beijing 100841, China;2.School of Electronic Engineering,Naval University of Engineering, Wuhan 430033, China)

Abstract:Thepolarimetricsyntheticapertureradar(SAR)isakindofindispensablemeansofremotesensingandmilitaryreconnaissance,buttheimagesneedaprecisemodelingandanalysistointerpret.TheKdistributionisusuallyusedtomodelpolarimetricsyntheticapertureradar(SAR)imageinthenon-Gaussiancase,butthebiasestimationoftheparametersaffectthefittingprecisionofthemodel.Inthispaper,theprobabilitydensityfunctionandthemaximumlikelihood(ML)estimationforthedeterminantofKdistributionmatrixarederived.Itsvalidityisalsoconfirmedbythesimulateddata.Then,theMLmethodisappliedtotheestimationofequivalentnumberoflooks(ENL)inPolSARimages.ComparesaremadebetweentheMLmethodandtheformermethodusingthedeterminantofthemeanofmatrix.Theresultsofexperimentsbasedonsimulatedandrealdatashowthattheproposedalgorithmobviouslypromotestheestimationbiasandvariance,whichisofpracticalvalueinsolvingtheaccurateestimationproblemforKdistributionregionsinpolarimetricSARimagery.

Keywords:K distribution; radar image; maximum likelihood estimation; covariance matrix

doi:10.13442/j.gnss.1008-9268.2016.02.013

收稿日期：2016-03-12

中图分类号：TN95

文献标志码：A

文章编号：1008-9268(2016)02-0071-06

作者简介

资助项目： 国家自然科学基金(批准号:61372165)

联系人： 晏庆E-mail: 63934470@qq.com