微电网黑启动中考虑DG特性与线路投入顺序的串行恢复策略
2016-06-21杨智豪牟龙华
杨智豪,牟龙华,刘 仲
(同济大学电气工程系,上海 201804)
微电网黑启动中考虑DG特性与线路投入顺序的串行恢复策略
杨智豪,牟龙华,刘 仲
(同济大学电气工程系,上海 201804)
制定合理的孤立微电网黑启动恢复策略对于加快微电网的恢复进程、减少事故损失具有重要意义。提出了一种适用于微电网黑启动的串行恢复策略。首先分析了分布式电源(Distributed Generation, DG)与大电网中传统火电机组所不同的特性,在此基础上建立了基于变异系数法的DG黑启动能力评估模型,并用于选取黑启动电源。然后以线路重要度和节点重要度作为网架重构的指标,建立了网架重构优化模型,并采用遗传算法进行求解。在求解出目标网架后,以单位时间内恢复发电量最大为目标,进一步确定线路的投入顺序。最后通过算例的分析及结果验证了所提方案的有效性。
微电网;黑启动;DG特性;变异系数法;遗传算法;串行恢复
0 引言
微电网通过统一管理分布式电源、储能单元、负荷以及控制保护单元,实现了分布式电源的高效利用,较好地解决了分布式电源对大电网造成冲击的问题[1-2]。微电网黑启动,是指在整个微电网因外部或内部故障导致停运而进入全黑状态后,不依靠大电网或其他微电网的帮助,仅通过启动微电网内部具有黑启动能力的 DG,进而带动其它非黑启动DG,逐步扩大恢复范围,最终实现整个微电网的恢复[3-4]。有效的微电网黑启动将会大大提高微电网的供电可靠性,同时也能为大电网的黑启动提供一定的支持。因此,研究微电网的黑启动对快速恢复系统供电具有重要意义。
通常将黑启动过程分为电源黑启动、网架重构和负荷恢复三个阶段[5]。其中,网架重构阶段是整个恢复过程中承上启下的阶段,主要目的是在尽可能短的时间内使各待恢复电源重新并网发电,通过恢复重要节点和关键线路搭建主网架,为全面恢复负荷打下基础[6]。文献[7]研究了机组累积启动时间与机组停机时间之间的关系,制定了网架重构策略,但未考虑线路的拓扑特性。文献[8]在网架恢复的优化计算中,将节点收缩后的网络凝聚度作为节点的重要度,并用作机组和负荷重要性的评价指标,但忽略了节点所带负荷的重要性。文献[9]提出了一种基于串行和并行恢复的系统重构优化算法,该算法采用分步寻优的方式,使得恢复过程中能够协调各子系统的同步恢复,但该方法主要针对传统大电网。文献[10]针对低压微电网,提出了基于多代理技术的微电网黑启动恢复控制策略,但所研究的微电网中 DG、负荷及线路数目较少,且主要侧重于微电网黑启动控制。文献[11]通过分层多代理的控制使具有黑启动能力的几个微电源预启动和同步运行,从而实现微电网的黑启动,但未对DG的黑启动能力进行评估。
一方面,考虑到常规微电网的规模远比传统大电网的规模小,微电网串行恢复所需时间和并行恢复所需时间实际相差不会很大;另一方面,考虑到目前仍难以有效地解决微电网并行恢复过程中的同期并列问题[12]。因此,本文提出了一种适用于微电网黑启动的串行恢复策略,该策略首先根据DG的特性建立了DG的黑启动能力评估模型,并用于选取黑启动电源。然后以线路重要度和节点重要度作为网架重构的指标,建立网架重构优化模型并采用遗传算法进行求解。在求解出目标网架后,以单位时间内恢复发电量最大为目标,进一步确定线路的投入顺序。
1 DG 特性分析及黑启动能力评价模型
1.1 DG 特性分析
传统大电网的黑启动已有较多的研究,对于微电网黑启动具有一定的借鉴意义,但是传统火电机组与DG之间存在着较大的差异,这使得传统大电网的黑启动方案并不适用于微电网。因此,在制定微电网黑启动方案时需着重考虑DG的特性。与传统火电机组相比,DG 的特性主要有以下五个方面。
(1) DG 的输出功率具有间歇性
在微电网中,风力发电的输出功率会随着风速的变化而产生波动,光伏发电的输出功率也会因为光照强度的变化而产生波动,两者都具有间歇性的特点。而传统火电机组则可以根据发电计划人为调整其输出功率。
(2) DG 的启动无需外部电源
DG 的运行输出主要依靠周围的自然条件,具有独立运行的能力,比如当光照强度达到光伏发电的最低要求时,光伏发电系统便可自启动输出功率,不需要提供额外的启动电能。而传统火电机组在启动时一般需要启动电能,具有厂用电负荷高的特点。
(3) DG 的启动不受启动时限的约束
传统火电机组的启动根据汽缸温度分为热启动、温启动、冷启动。为了保护汽缸不受较大温差产生的热应力破坏,需要控制汽缸的升温速度,这也导致了温启动和冷启动的启动时间较长,因此在传统大电网黑启动中通常优先考虑恢复具备热启动条件的机组,需要考虑火电机组的热启动时限约束。而DG则没有传统火电机组的启动时限约束,相应的微电网的黑启动会更加快速。
(4) DG 具有多种控制方式
大多数DG输出的电能质量不符合并网要求,必须使用电力电子装置进行功率转换。DG 的控制方式主要有:PQ 控制、V/f控制、下垂控制、虚拟同步发电机等,可以根据具体情况采用不同的控制方式。
(5) DG 可通过配带储能装置改善电能质量
对于带储能装置的 DG,可以利用储能装置快速调节的特性减缓DG输出功率的波动,为微电网提供稳定的电压和频率,因此可以采用 V/f控制方式。对于不带储能装置的 DG,由于其输出功率具有间歇性,不能要求其按照负荷的需求发电,因此通常采用PQ控制方式。
1.2 DG 黑启动能力评价模型
DG的黑启动能力是指不借助于外部电源的帮助,仅依靠自身启动电源平稳启动,并能在启动后给一定量的负荷提供稳定供电的能力[13]。根据对DG 黑启动能力的定义,本文选取了如下黑启动能力的评价指标:DG 的容量、DG 的启动时间、DG的带载能力、DG 的调压调频能力和 DG 所带储能的荷电状态(State of Charge, SOC)。
可采用变异系数法[14]对各黑启动能力的评价指标赋予权重,建立基于变异系数法的DG黑启动能力评价模型。变异系数法是一种客观的赋权方法,差异越大的指标越能体现出被评价对象之间的优劣,也因此会赋予其越大的权重,具体的步骤如下所述。
(1) 建立评价矩阵
设有 n个对象,评价指标为 m 个,第 i个对象的评价指标向量记作,则评价矩阵。第 j个指标权重用表示,则指标权重向量为
(2) 指标规范化
对于正向指标,即指标数值越大越好的“效益型”指标。

对于负向指标,即指标数值越小越好的“成本型”指标。

(3) 指标权重计算
在各指标规范化处理后,分别采用式(3)和式(4)计算各指标的平均值和标准差。

接下来采用式(5)计算各项指标的变异系数为

其中:Vj是第 j项指标的变异系数;为第j项指标的平均值;sj为第 j项指标的标准差。
则各项指标的权重为

(4) 综合评分
评价矩阵X和权重向量w的乘积便是各对象的综合评分向量G,即

最后根据模型的综合评分选取黑启动电源,并将其作为率先恢复的对象。
2 微电网网架重构模型
2.1 网架重构指标
网架重构阶段的主要目的是使各待恢复电源快速并网发电,通过恢复关键线路和重要节点搭建骨架网络,为全面恢复负荷打下基础。因此,在确定骨架网络时,需要对线路和节点的重要度进行评价。
2.1.1 线路重要度
本文主要从线路拓扑特性、线路自身特性两个方面对线路的重要度进行评估。
考虑到优先恢复拓扑特性好的线路更有利于开展对后续网架的恢复,因此对线路重要度进行评估时需要计及其拓扑特性。本文采用线路介数对线路的拓扑特性进行定量地评价,介数的概念是由Freeman 于 1979 年提出,线路介数值越大,说明该线路在网络中的作用越大,剔除线路介数值大的线路会造成大量节点对之间的距离变长。本文定义线路介数为线路被网络中所有最短路径经过的次数占最短路径总数的比例,其表达式为

式中:Jk为线路 k 的线路介数值;为网络中任意两点之间最短路径经过线路 k的次数;为网络中任意两节点间的最短路径数目;为网络中所有节点的集合。
对于线路自身特性的重要度评估,本文采用文献[15]所述的线路操作时间对线路赋权,选择恢复线路操作时间短的线路可以减少系统恢复的时间,从而减少停电损失。通常根据操作人员的经验确定乐观操作时间L,悲观操作时间P以及最可能估计时间 M,而线路 k 的实际操作时间 tk则在 L 和 P 之间呈贝塔分布。
由于线路介数和线路操作时间的量纲不同,因此需要对其进行归一化处理,取线路介数的最大值作为其基准值,取线路操作时间的最小值作为其基准值。则线路重要度定义为

2.1.2 节点重要度
对于节点重要度,本文主要从节点所带的负荷量和负荷等级进行评估。负荷等级一般分为三级,在相同负荷量的情况下,负荷等级越大其停电损失越大,节点重要度也越大。定义节点重要度为

2.2 网架重构模型
2.2.1 目标函数
在确定目标网架时,综合考虑了线路拓扑重要性、线路操作时间以及节点所带负荷的重要性,即要求所搭建的骨架网络能够兼顾对重要线路和重要节点的恢复。重构的网架越大,其恢复重要线路和重要节点也就越多,但恢复所需的时间会越长,操作的次数会越多,失败的风险也越大。因此,本文采用目标网架中线路平均重要度和节点平均重要度作为重构标准,则网架重构模型的优化目标函数为

式中:Li为归一化后线路 i的重要度;Wj为归一化后节点 j的重要度;V为目标网架中所有线路的集合;E为目标网架中所有节点的集合;n为目标网架中的线路数;m为目标网架中的节点数。
2.2.2 约束条件
在重构过程中,需要考虑的约束条件如下所述。
(1) 发电机出力约束

(2) 节点电压约束
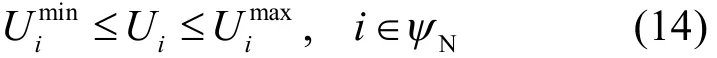
(3) 线路约束

(4) 节点功率平衡约束

2.3 模型求解
微电网网架重构问题在数学上是一个带约束条件的非线性优化问题,可采用遗传算法[16]进行求解。遗传算法的求解步骤如下所述。
(1) 编码及初始化
本文采用网络中线路的启用状态作为基因,将每条线路的状态组合在一起形成一条染色体,染色体的长度即为线路总数。对每一条线路进行编码,若某条线路被选中,则在染色体中与其对应的位置取 1,否则取 0。
(2) 有效性检测
由于遗传算法的更新迭代过程是一个随机优化过程,无法保证所选中的线路之间具有拓扑连通性。若各DG之间能够互相连通,则属于有效个体;否则需要对个体进一步改造,可采用最短路径法搜索已选中状态的区域到未互连DG的路径,并将该路径改为选中状态,使其成为有效个体。
(3) 适应度函数
对于约束条件式(12)~式(17),主要为潮流约束条件,可通过调控DG的发电量和负荷的投入量使其满足约束。因此,本文直接采用式(11)作为适应度函数。
(4) 选择操作
选择操作通过适应度选择优质个体而抛弃劣质个体,本文采用轮盘赌选择方法,保证了当前适应度最优的个体能够进化到下一代而不被遗传操作的随机性破坏,保证算法的收敛性。
(5) 交叉操作
交叉是指对两个相互交叉的染色体按某种方式相互交换其部分基因,从而形成两个新的个体。本文采用均匀交叉方式,两个相互配对个体的每一位基因都以相同的概率进行交换,从而形成两个新个体。
(6) 变异操作
变异是指将个体染色体编码串中的某些基因座上的基因值用该基因座的其他等位基因来替换,从而形成一个新的个体。本文采用基本位变异,即对个体编码串以变异概率随机指定某一位或某几位基因进行变异操作。对变异操作后的新个体进一步通过步骤(2)检测其有效性。
(7) 终止条件
当满足给定的允许误差或迭代次数达到设定的最大迭代次数时,终止运算算并输出最优解,否则返回步骤(3)继续迭代运算,直到满足终止条件。
2.4 线路投入顺序
通过遗传算法可求解出重构的目标网架,但并未确定目标网架中每条线路的投入顺序,因此还需进一步确定目标网架中的线路投入顺序。
为了能在更短时间内恢复更多的发电量,本文以单位时间内恢复发电量最大为目标,对线路的投入顺序进行确定。在求解出的目标网架中,搜索黑启动 DG 到各待恢复 DG 的恢复路径,按式(18)计算各DG的发电量与对应恢复路径所需操作时间的比值 F,F值代表该路径单位时间内所能恢复的供电量,选取F值大的路径优先恢复,可以提高系统恢复供电的效率。接着,继续在目标网架中搜索已恢复供电的区域到各待恢复DG的恢复路径,按照上述的方法确定下一条投入恢复的路径,直至所有待恢复的DG并网。

2.5 微电网重构的串行恢复策略
微电网重构的串行恢复策略步骤如下所述。
步骤 1:读入各 DG 的参数,主要包括 DG 的容量、启动时间、带载能力、调压调频能力以及DG所带储能装置的 SOC。对于不带储能的风机和光伏,其 SOC 指标为 0;对于微型燃气轮机,则假定其燃气充足,能够一直保持良好稳定的输出功率,因此其 SOC 指标为 1。通过 DG 黑启动能力评价模型,得到各DG的黑启动能力评分,并选取出最优的黑启动DG。
步骤 3:按照 2.2 小节所述,建立重构模型并用遗传算法进行求解。
步骤 4:在求解出的目标网架中,按照 2.4 小节所述的方法,以单位时间内恢复发电量最大为目标对线路投入顺序进行确定。
步骤 5:在恢复过程中,黑启动 DG 采用 V/f控制方式,提供稳定的参考电压和频率。当黑启动DG与待恢复DG连接时,待恢复DG以黑启动DG提供的电压和频率为参考,通过 PQ 控制方式启动并网。
3 算例分析
参照文献[17],本文采用修改后的 IEEE30 节点微电网系统,通过 Matlab 软件编程计算,验证所提方法的有效性。
修改后的 IEEE30 节点微电网结构如图1 所示,该微电网系统包括 7 个 DG,30 个负荷节点以及 41条线路。首先求解DG 黑启动能力评价模型,各DG的指标参数与黑启动能力评价结果如表1所示。由于本文采用的是串行恢复策略,所以只选取黑启动能力最优的 DG 作为黑启动电源,即。作为黑启动电源采用 V/f控制方式,为整个恢复过程提供稳定的参考频率和参考电压。
进一步,通过 Betweenness_Centrality 算法计算各线路被网络中所有最短路径经过的次数,进而计算出各线路介数,从大到小列出排在前 20 位的线路,其归一化后的线路介数值如表2所示。
由于遗传算法是一种随机算法,所以需要在同样的网络条件参数下进行多次独立运算,并选择适应度最高的作为最优目标网架。本文对遗传算法的基本参数设定如下:种群规模为 100,交叉概率为0.8,变异率为 0.02,遗传代数 150。计算得到的网架重构方案如图2所示,其中实线为重构恢复的线路,虚线为未恢复的线路。

图1 修改后的 30 节点微电网结构Fig. 1 Modified structure of 30-bus microgrid

表1 DG 的各项参数Table 1 Parameters of DGs

表2 归一化的 30 节点微电网线路介数值Table 2 Normalized line betweenness value of 30-bus microgrid

图2 网架重构结果Fig. 2 Results of network reconstruction
重构的网架包括有线路 1-2,1-3,2-4,4-6,4-12,6-10,6-28,10-22,12-13,22-24,23-24,27-28。这些线路大多是表2 中的线路,线路介数值都很高,即被网络中最短路径经过的次数最多,它们的优先恢复更有利于下一阶段给其他节点恢复供电,加快了恢复进程,减少了停电损失。
在求解出目标网架后,需要进一步确定线路的投入顺序。根据 2.4 小节所述的方法,在目标网架中,搜索黑启动DG到各待恢复DG 的路径,计算其F值,F值的计算结果如表3所示。由表3可知,DG2→DG1的 F 值最大,因此率先投入线路 2-1,使DG1恢复并网。接着,在目标网架中继续搜索已恢复供电的区域到各待恢复DG的路径,选取F值最大的路径作为下一条投入恢复的路径,线路投入顺序如表4所示。

表3 F 值计算结果Table 3 Value of function F

表4 线路投入顺序Table 4 Restoration sequence of lines
4 结论
本文在分析DG特性的基础上,提出了一种适用于孤立微电网黑启动的串行恢复策略,首先建立了DG黑启动能力评价模型并用于选取最优的黑启动 DG,然后建立了兼顾恢复重要线路和重要节点的网架重构优化模型,采用遗传算法求解重构模型。
在求解出的目标网架中,以单位时间内恢复发电量最大为目标,进一步确定线路的投入顺序。最后通过修改后的 30 节点微电网的算例分析,验证了所提方案的可行性。
[1]曹智平, 周力行, 张艳萍, 等. 基于供电可靠性的微电网规划[J]. 电力系统保护与控制, 2015, 43(14): 10-15.CAO Zhiping, ZHOU Lixing, ZHANG Yanping, et al. Micro-grid planning based on supply reliability[J]. Power System Protection and Control, 2015, 43(14): 10-15.
[2]成思琪, 刘俊勇, 向月, 等. 微网中混储/柴协调运行策略研究[J]. 电力系统保护与控制, 2015, 43(7): 42-50. CHENG Siqi, LIU Junyong, XIANG Yue, et al. Research on optimal coordinated operation for microgrid with hybrid energy storage and diesel generator[J]. Power System Protection and Control, 2015, 43(7): 42-50.
[3]牟龙华, 夏明栋, 刘仲. 微电网的黑启动研究[J]. 电力系统保护与控制, 2014, 42(22): 32-37. MU Longhua, XIA Mingdong, LIU Zhong. Research on black-start for microgrid[J]. Power System Protection and Control, 2014, 42(22): 32-37.
[4]刘仲, 牟龙华, 杨智豪. 大停电后含分布式电源的电网 分区及负 荷恢复方案 [J]. 电力系统 保护与 控制, 2015, 43(22): 55-61. LIU Zhong, MU Longhua, YANG Zhihao. Scheme for partitioning and load restoration of power grid containing distributed generation after blackout[J]. Power System Protection and Control, 2015, 43(22): 55-61.
[5]刘仲, 牟龙华, 许旭峰. 微电网黑启动中考虑负荷恢复优化的分布式电源恢复方案[J]. 电力自动化设备, 2016, 36(3): 46-52. LIU Zhong, MU Longhua, XU Xufeng. Microgrid black-start considering DG startup sequence and load restoration optimization[J]. Electric Power Automation Equipment, 2016, 36(3): 46-52.
[6]刘玉田, 王洪涛, 叶华. 电力系统恢复理论与技术[M].北京: 科学出版社, 2014.
[7]周敏, 刘艳. 计及火电机组启动过程的网架并行恢复策略[J]. 电力系统自动化, 2011, 35(10): 30-34. ZHOU Min, LIU Yan. A parallel restoration strategy for power network considering the start-up process of thermal units[J]. Automation of Electric Power Systems, 2011, 35(10): 30-34.
[8]LIU Yan, GU Xueping. Skeleton-network reconfiguration based on topological characteristics of scale-free networks and discrete particle swarm optimization[J]. IEEE Transactions on Power Systems, 2007, 22(3): 1267-1274.
[9]赵腾, 张焰, 张志强. 基于串行及并行恢复的电力系统重构[J]. 电力系统自动化, 2015, 39(14): 60-67. ZHAO Teng, ZHANG Yan, ZHANG Zhiqiang. Power system reconstruction based on hierarchical and partitioned restoration[J]. Automation of Electric Power Systems, 2015, 39(14): 60-67.
[10]MOREIRA C L, RESENDE F O, PEAS LOPES J A. Using low voltage microgrids for service restoration[J]. IEEE Transactions on Power Systems, 2007, 22(1): 395-403.
[11]CAI Niannian, XU Xufeng, MITRA J. A hierarchical multi-agent control scheme for a black start-capable microgrid[C]// Power and Energy Society General Meeting, 2011 IEEE. IEEE, 2011: 1-7.
[12]黄杏. 微网系统并/离网特性与控制策略研究[D]. 北京: 北京交通大学, 2013. HUANG Xing. Grid-connected/islanding characteristics and control strategies of microgrid[D]. Beijing: Beijing Jiaotong University, 2013.
[13]牟龙华, 夏明栋, 刘仲. 孤立微网中微源的黑启动能力 [J]. 同 济 大 学 学 报 (自 然 科 学 版 ), 2015, 43(12): 1877-1887. MU Longhua, XIA Mingdong, LIU Zhong. Research on black-start capability of microsources in isolated microgrid[J]. Journal of Tongji University (Natural Science), 2015, 43(12): 1877-1887.
[14]张文朝, 顾雪平. 应用变异系数法和逼近理想解排序法 的 风 电 场 综 合 评价 [J]. 电 网 技 术, 2014, 38(10): 2741-2746. ZHANG Wenchao, GU Xueping. Comprehensive evaluation of wind farms using variation coefficient method and technique for order preference by similarity to ideal solution[J]. Power System Technology, 2014, 38(10): 2741-2746.
[15]曾顺奇, 文福拴, 薛禹胜, 等. 计及操作时间不确定性的电力系统网架重构策略优化[J]. 电力系统自动化, 2011, 35(23): 16-21. ZENG Shunqi, WEN Fushuan, XUE Yusheng, et al. Optimization of network reconfiguration strategy for power systems considering operating time uncertainty[J]. Automation of Electric Power Systems, 2011, 35(23): 16-21.
[16]李泽文, 易志鹏, 杨毅, 等. 基于遗传算法的电网故障行波定位装置的优化配置[J]. 电力系统保护与控制, 2015, 43(3): 77-83. LI Zewen, YI Zhipeng, YANG Yi, et al. Optimal placement of traveling wave fault location equipment for power grid based on genetic algorithm[J]. Power System Protection and Control, 2015, 43(3): 77-83.
[17]彭克, 王成山, 李琰, 等. 典型中低压微电网算例系统设计[J]. 电力系统自动化, 2011, 35(18): 31-35. PENG Ke, WANG Chengshan, LI Yan, et al. Design of a typical medium-low voltage microgrid network[J]. Automation of Electric Power Systems, 2011, 35(18): 31-35.
(编辑 姜新丽)
A serial restoration strategy considering characteristics of DG and line restoration sequence for black start of microgrid
YANG Zhihao, MU Longhua, LIU Zhong
(Department of Electrical Engineering, Tongji University, Shanghai 201804, China)
Developing a rational restoration strategy for black start of isolated microgrid helps to speed up the system restoration and reduce the loss. A serial restoration strategy, which is suitable for black start of microgrid, is proposed. Firstly, on the basis of the different characteristics between distributed generation (DG) and traditional unit, an evaluation model, which is used to assess the black start capability of DG and select the black-start generation, is established based on the variation coefficient method. Secondly, a network reconfiguration optimization model is built by taking the node importance and the line importance as the indicators, and the model is solved by genetic algorithm. Then, the restoration sequence of lines is determined by maximizing the restored generation capacity in per unit time. Finally, the simulation results verify the validity of the proposed scheme.
This work is supported by National Natural Science Foundation of China (No. 51407128).
microgrid; black start; characteristics of DG; variation coefficient method; genetic algorithm; serial restoration
10.7667/PSPC201634
:2016-05-26
杨智豪(1991-),男,硕士研究生,研究方向为微电网黑启动、微电网保护;E-mail: 1433130@tongji.edu.cn
牟龙华(1963-),男,教授,博士生导师,研究方向为电力系统继电保护、分布式发电与微电网、电能质量;E-mail: lhmu@tongji.edu.cn
刘 仲(1991-),男,硕士研究生,研究方向为微电网黑启动、微电网保护。E-mail: zeakyleo@163.com
国家自然科学基金资助项目(51407128)
