扩展卡尔曼滤波器的目标机动信息估计研究

曹有亮，张金鹏

(中国空空导弹研究院，河南 洛阳　471009)



扩展卡尔曼滤波器的目标机动信息估计研究

曹有亮，张金鹏

(中国空空导弹研究院，河南 洛阳471009)

摘 要:针对目标机动信息估计时的状态方程非线性及目标机动频率未知的特点,对三维线性卡尔曼滤波器的状态量进行了扩维。利用扩展卡尔曼滤波器(EKF)完成了目标机动信息估计算法设计,并通过仿真验证了不同条件下滤波器对目标机动频率、机动加速度及加加速度的估计特性。同时,对滤波器估值误差的收敛性进行了仿真评估,验证了算法的有效性。

关键词:扩展卡尔曼滤波器;目标机动估计;非线性状态方程

0引言

在末制导过程中，对于非机动目标，采用比例制导律可以达到满意的制导精度, 而且在一定的线性化简化条件下，可以证明比例制导律的最优性。但是目标的机动会严重影响比例导引的性能，导致脱靶量增大。为了改善制导回路的性能，减小脱靶量，需要在制导律设计中对目标机动加速度进行补偿，如在比例制导律基础上增加目标机动补偿项而得到扩展比例制导律，此时目标机动信息的准确性将对制导性能产生较大影响。

对于目标机动信息的估计问题，广泛采用卡尔曼滤波方法进行处理，在研究中一般需要假设目标的机动模型及随机机动的统计特性。本文假设导弹采用雷达导引头, 可以提供视线角和相对距离、弹目接近速度信息作为系统的输出，针对寻的末制导中状态方程与观测方程非线性以及目标机动频率未知的特点，利用扩展卡尔曼滤波器(EKF)设计目标机动信息估计算法，对目标机动频率、机动加速度及加加速度估计的准确性进行仿真，验证滤波器误差的收敛性。

1扩展卡尔曼滤波算法(EKF)

若系统状态方程与观测方程为非线性形式，则可采用扩展卡尔曼滤波器，其处理步骤为

(1)

(2)

(3)

为了减小线性化误差，提高滤波跟踪精度，可将非线性方程的泰勒级数截断至二阶项，得到二阶扩展卡尔曼滤波器，其滤波过程如下：

(4)

(5)

(6)

扩展卡尔曼滤波在目标状态预测值处对非线性观测进行线性近似，若能在更加精确的状态估计值处做近似，可以预知线性化误差更小，滤波估计精度更高，因此在状态估计值处线性化对状态进行再次更新，这种处理可以一直迭代下去，称为迭代卡尔曼滤波。其处理步骤为

(7)

2基于EKF的目标机动信息估计

假设目标的机动形式为正弦机动，实际上无论是逃逸机动还是蛇形机动，在惯性系中都可以认为是一种正弦机动，所以此假设具有一定的合理性。目标正弦机动的寻的回路模型见图1。

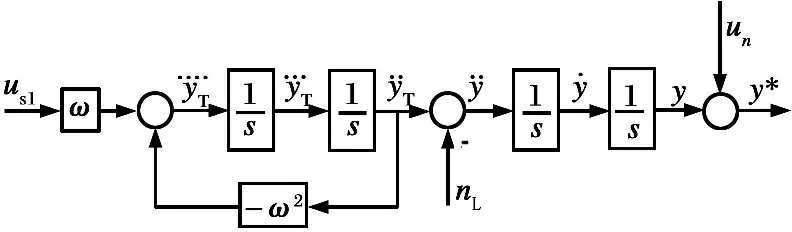
图1正弦机动的寻的回路模型

也可用状态空间方程来描述上述系统：

(8)

式中： us1和us2为过程噪声。过程噪声us1的功率谱密度如下：

式中： ωEXP为目标最大可能的机动频率； nTMAX为目标最大机动值； tF为整个飞行时间。us2的功率谱密度Φs2则需要通过系统试验来获得。

由于引入目标机动频率为状态量，系统状态方程将为非线性。以此为基础的滤波器也将为非线性扩展卡尔曼滤波器，而不是线性卡尔曼滤波器。但此模型的测量方程仍然为线性的，如下所示：

(9)

系统动态特性矩阵可以通过对系统状态方程求偏导得到：

(10)

根据系统状态方程，可计算得到系统动态特性矩阵：

(11)

可以使用一个二阶泰勒展开式来得到近似的基本矩阵：

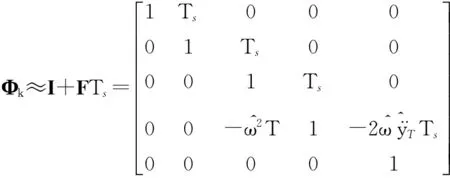
(12)

根据状态方程，可得连续过程噪声矩阵：

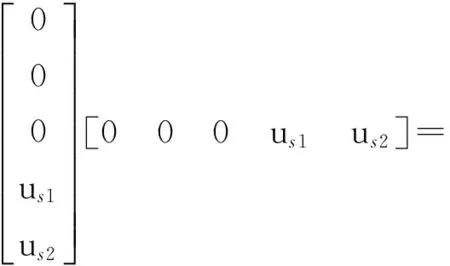
(13)

式中： 频谱密度Φs1和Φs2之前已经定义。离散过程噪声矩阵可以依据下式通过连续过程噪声矩阵得到：

(14)

将连续过程噪声矩阵和基本矩阵代入式(14)，可得离散过程噪声矩阵：

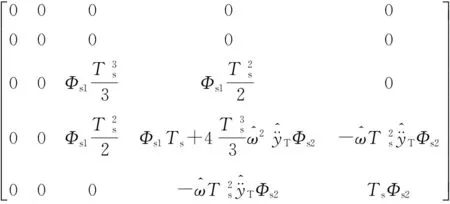
(15)

当滤波器工作时，卡尔曼增益是从Ricatti矩阵方程式计算得到。Ricatti矩阵方程是一系列递归矩阵方程式，如下：

(16)

式中：Pk为协方差矩阵，代表更新前的状态估值误差； Mk也为协方差矩阵，代表更新后的状态估值误差。

在得到卡尔曼增益矩阵Kk后，扩展卡尔曼滤波器的状态估计方程为

(17)

3仿真验证

为了启动Ricatti方程式，需要初始方差矩阵，该矩阵表示估值中的初始不确定值。为初始方差矩阵选择适当的值是滤波器设计的一项关键技术。本文的仿真中，利用真值对初始方差矩阵进行初始化，工程上可对目标传感器的精度进行测试和评估，然后设计合理的方差矩阵。

为了验证滤波算法的有效性，引入一个幅值为3g且机动频率ω为2rad/s的目标正弦机动，利用EKF滤波递推算法对其进行估计。在测角方差为1mr，频谱密度Φs2为0且机动频率初始值为-1rad/s的情况下，仿真结果如图2～4所示。

从图2～4可以看出，机动频率初始值为-1rad/s的情况下，目标机动频率估值在稳态为-2.5rad/s左右，模值基本接近真值。在测角方差为1mr的情况下，加速度和加加速度的估值在大部分情况下严重偏离真值，只是在飞行时间末端收敛在真值附近。将测角方差降低至0.1mr且机动频率初始值为1rad/s，仿真结果如图5～9所示。

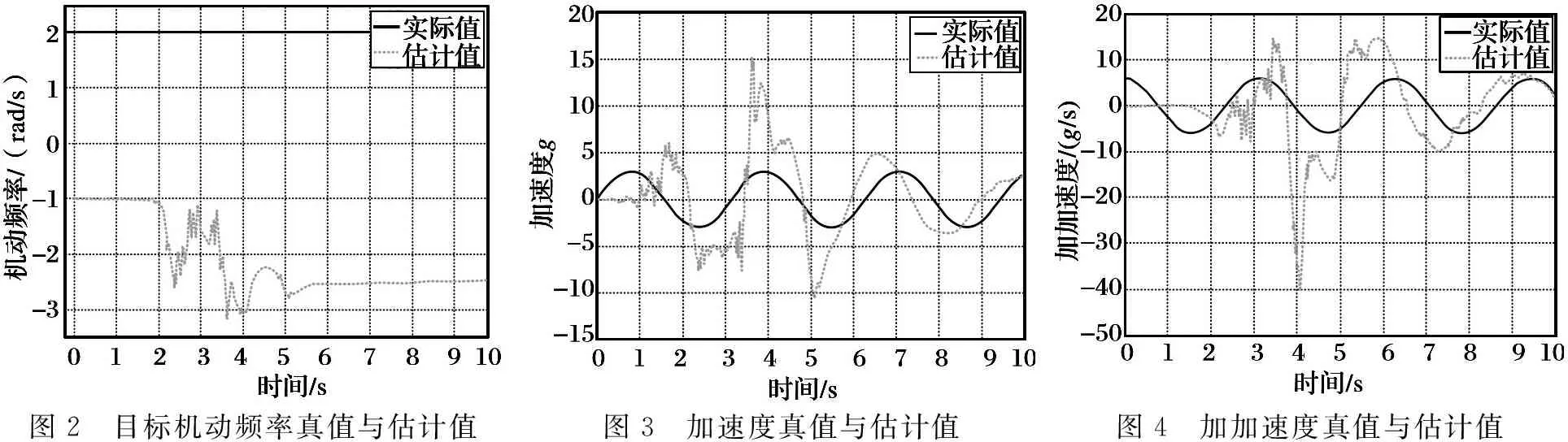
图2 目标机动频率真值与估计值图3 加速度真值与估计值图4 加加速度真值与估计值

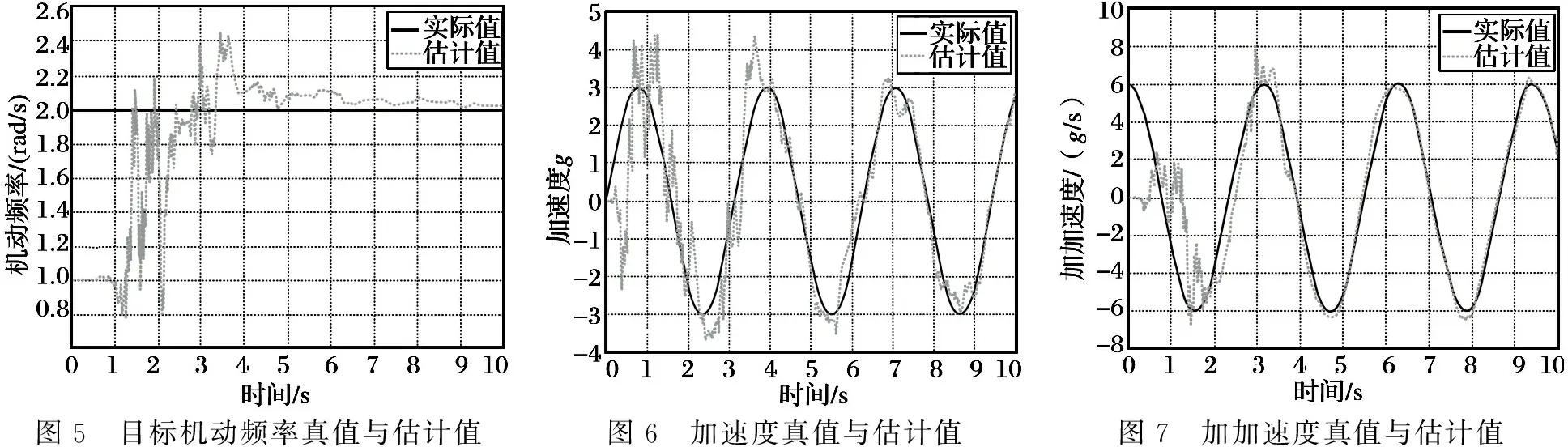
图5 目标机动频率真值与估计值图6 加速度真值与估计值图7 加加速度真值与估计值

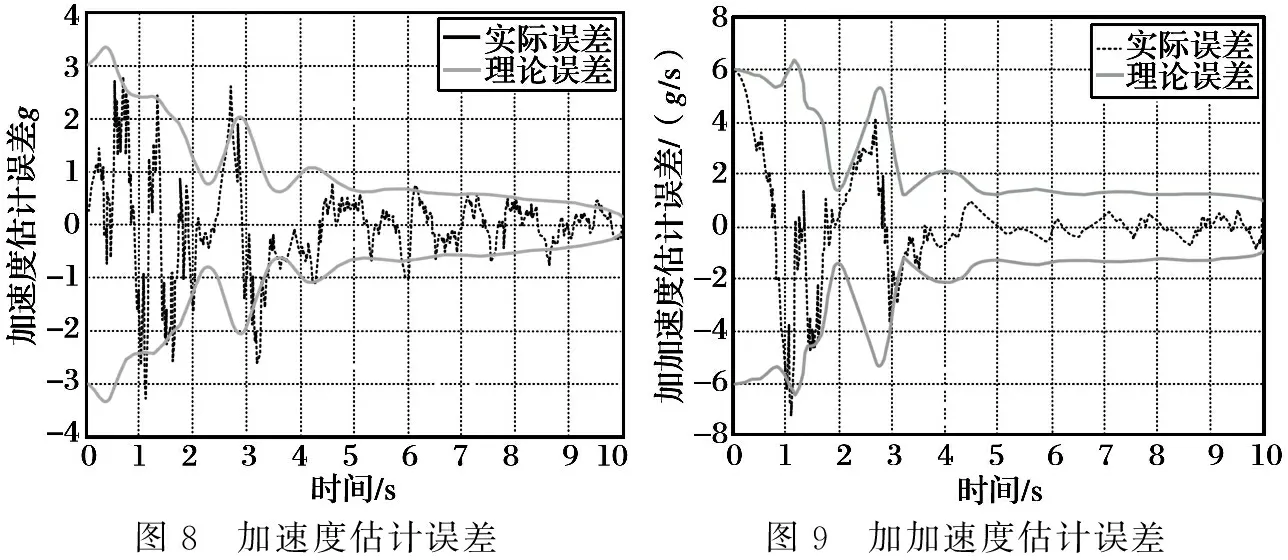
图8 加速度估计误差图9 加加速度估计误差

从图5～9的仿真结果可看出，在降低测量噪声及机动频率初值误差较小的情况下，加速度和加加速度在大部分飞行时间内都得到准确的估计，机动频率也很快收敛到真值附近，估值误差与理论值较相符。

4结论

本文针对目标机动信息估计时状态方程非线性及目标机动频率未知的特点，利用扩展卡尔曼滤波器(EKF)完成了目标机动信息滤波算法的设计。仿真验证表明在较小测角噪声下滤波器对目标机动频率、机动加速度及加加速度具有良好的估计准确性，可以为制导系统及制导律提供更良好准确的目标机动信息，改善制导系统精度。

参考文献：

[1] 马克茂，贺风华，姚郁.目标机动加速度的估计与导引律实现[J]. 宇航学报, 2009, 30(6): 2213-2219.

[2] 范红旗, 樊建鹏, 付强. 机动目标运动建模技术综述[C]∥ 国防科大电子科学与工程学院2011年会论文集, 2012.

[3]ZarchanP.TacticalandStrategicMissileGuidance[M].AIAA，1997.

[4] 安相宇，董朝阳，王青. 一种基于EKF技术的天线罩瞄准误差补偿方法[J]. 系统仿真学报, 2007, 20(15):4099-4103.

[5]BrysonAE,HoYC.AppliedOptimalControl[M].NewYork:Blaisdell, 1969.

[6] 周荻.寻的导弹新型导引规律[M].北京：国防工业出版社，2002.

[7] 黄晓雷，牛申阁. 扩展卡尔曼滤波在无人机航迹控制系统中的应用研究[J]. 航空兵器，2008(2)：11-13.

[8] 沈亮，万平，耿源. 雷达导引头自适应卡尔曼滤波算法研究[J]. 航空兵器，1994(2)：30-37.

[9] 葛泉波，李文斌，孙若愚，等. 基于EKF的集中式融合估计研究[J]. 自动化学报，2013，39(16)：816-825.

Researeh on Target Maneuvering Information Estimation Method of EKF

Cao Youliang, Zhang Jingpeng

(China Airborne Missile Academy，Luoyang 471009，China)

Abstract:For the characteristics of the nonlinear state equation and the unknown target maneuvering frequency on target maneuvering information estimation, the state of three-dimensional linear Kalman filter is extended. The extended Kalman filter is used to design target maneuvering information estimation algorithm, and by simulation the estimate characteristics of target maneuveing frequency, acceleration and jerk under different conditions are verified. The convergence of the estimation error is simulated and evaluated, and the effectiveness of the algorithm is verified.

Key words:EKF; target maneuver estimation; nonlinear state equation

DOI：10.19297/j.cnki.41-1228/tj.2016.01.007

收稿日期：2015-06-09

基金项目：航空科学基金项目(20110112001)

作者简介：曹有亮(1984-)，男，河南焦作人，硕士，工程师，研究方向为制导与控制技术。

中图分类号:TJ765

文献标识码:A

文章编号:1673-5048(2016)01-0040-05