蚁群算法解决CTSP问题的参数设置研究*

杨　惠　韩李涛,2　类延辉　郑　莹　吴佳怡

(1.山东科技大学测绘科学与工程学院　青岛　266590)(2.海岛(礁)测绘技术国家测绘局重点实验室　青岛　266590)(3.河北建筑工程学院　张家口　075000)



蚁群算法解决CTSP问题的参数设置研究*

杨惠1韩李涛1,2类延辉1郑莹3吴佳怡1

(1.山东科技大学测绘科学与工程学院青岛266590)(2.海岛(礁)测绘技术国家测绘局重点实验室青岛266590)(3.河北建筑工程学院张家口075000)

摘要由于蚁群算法中参数较多,设置不同的参数值对计算结果的影响很大,目前在参数设置方面尚缺乏足够的理论基础。对蚁群算法的基本原理及CTSP问题的解决进行了详细介绍,重点讨论分析了蚁群算法中的各个参数对其性能的影响以及参数的合理设置,并尝试采用参数循环组合的枚举方式对CTSP问题进行了求解,获得了更优的计算结果。

关键词蚁群算法; 中国旅行商问题; 参数设置

Class NumberTP301.6

1引言

蚁群算法是由意大利学者M. Dorigo等于20世纪90年代提出的一种新型的模拟进化算法,它具有正反馈性、并行性、分布式、鲁棒性等特点[1]。蚁群算法通过模拟蚂蚁寻找食物源的过程,利用其巧妙的搜索机制,在一系列复杂的组合优化问题求解中取得了很多成果。M. Dorigo等还将蚁群算法应用于解决经典的旅行商问题(TSP),并且得到了令人满意的计算结果[2]。蚁群算法这种来自生物界的智能仿生算法已经在交通、电力、通信等很多方面表现出相当好的性能,具有很大的发展潜力。

由于蚁群算法的参数空间范围很大,各参数之间的关联性十分紧密且没有明确的规律,找到最优的参数组合,使蚁群算法的各方面性能都达到最优是一个极其复杂的问题,这也是蚁群算法的重要研究方向。目前,蚁群算法的参数设置尚没有完善的理论依据和具体方法,通常人们都是让一个参数变化,另外几个参数固定不变的方法来对参数进行选择,显然这种方法忽略了参数之间的相互耦合。本文将蚁群算法应用于解决中国旅行商问题(Chinese TSP,CTSP),并通过实验对参数设置进行研究,以求出更好的结果。

2蚁群算法求解TSP问题

2.1蚁群算法基本原理

生物学家研究发现,像蚂蚁这种视盲动物是很难独立完成觅食的,自然界中的蚂蚁觅食是一种群体性的行为。蚂蚁在寻找食物源时会集体行动,每只蚂蚁在它经过的路径上释放一定量的信息素,并且能够检测其他蚂蚁释放的信息素。通常,蚂蚁会优先选择信息素浓度较高的路线移动,并释放自身的信息素,这就会增加该条路径上的信息素浓度,形成了正反馈现象,即信息素浓度强的路径更强,信息素浓度弱的则更弱。随着越来越多的蚂蚁通过该条路径,最终蚂蚁能够找到一条从巢穴到食物源的最短路径。同时人们发现,蚂蚁所释放的信息素会随着时间的推迟而逐渐减少。具体蚁群系统的工作原理见文献[3]。

2.2蚁群算法解决TSP问题基本原理

蚂蚁的数量设为m,城市的数量设为n,城市i与城市j之间的距离设为dij(i,j=1,2,…,n),t时刻在城市i与城市j之间路径上的信息素浓度用τij(t)表示。各个城市间连接路径上的初始信息素浓度相同,可设为τij(0)=τ0。

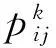
(1)

蚂蚁在释放信息素的过程中,两两城市间连接路径上的信息素浓度也在逐渐衰减,信息素的挥发程度用参数ρ(0<ρ<1)表示。因此,当所有蚂蚁完成一次路径循环后,各个城市间连接路径上的信息素浓度需要根据式(2)进行实时更新,即

(2)

针对蚂蚁释放信息素问题,M. Dorigo等曾给出三种不同的模型[2],分别称之为Ant Cycle System,Ant Quantity System,Ant Density System,其计算公式如下:

1) Ant Cycle System模型

(3)

其中,Q是一个常数,表示蚂蚁沿路径循环一次所释放的信息素总量;Lk为第k只蚂蚁经过路径的长度。

2) Ant Quantity System模型

(4)

3) Ant Density System模型

(5)

在以上三种模型中,Ant Cycle System模型利用蚂蚁搜索过的路径总长计算路径上的信息素浓度;Ant Quantity System模型则利用蚂蚁经过各个城市间的距离计算路径上的信息素浓度;而Ant Density System模型则将蚂蚁释放的信息素浓度值取为恒值,没有考虑到不同蚂蚁经过路径长短的影响。所以,一般都选用Ant Cycle System模型计算蚂蚁释放在路径上的信息素浓度,这个模型表示蚂蚁经过的路径长度越短,路径上的信息素浓度越高[4]。

2.3蚁群算法解决CTSP问题的基本步骤

蚁群算法解决CTSP问题一般需要以下几个步骤:计算城市间相互距离、设定初始化参数、构建解空间、更新信息素和判断是否终止,具体如图1所示。

1) 计算城市间相互距离:依据31个城市的位置坐标,计算两两城市之间的相互距离,得到对称的距离矩阵。

2) 初始化参数:对相关的参数进行初始化,如蚂蚁数量m、信息素重要程度因子α、启发函数重要程度因子β、信息素挥发因子ρ、信息素释放总量Q、最大迭代次数iter_max,迭代次数初值iter=1。

3) 构建解空间:将多个蚂蚁随机放置在不同的城市作为出发点,对每个蚂蚁计算其下一个待访问的城市,直到所有蚂蚁访问完所有的城市。

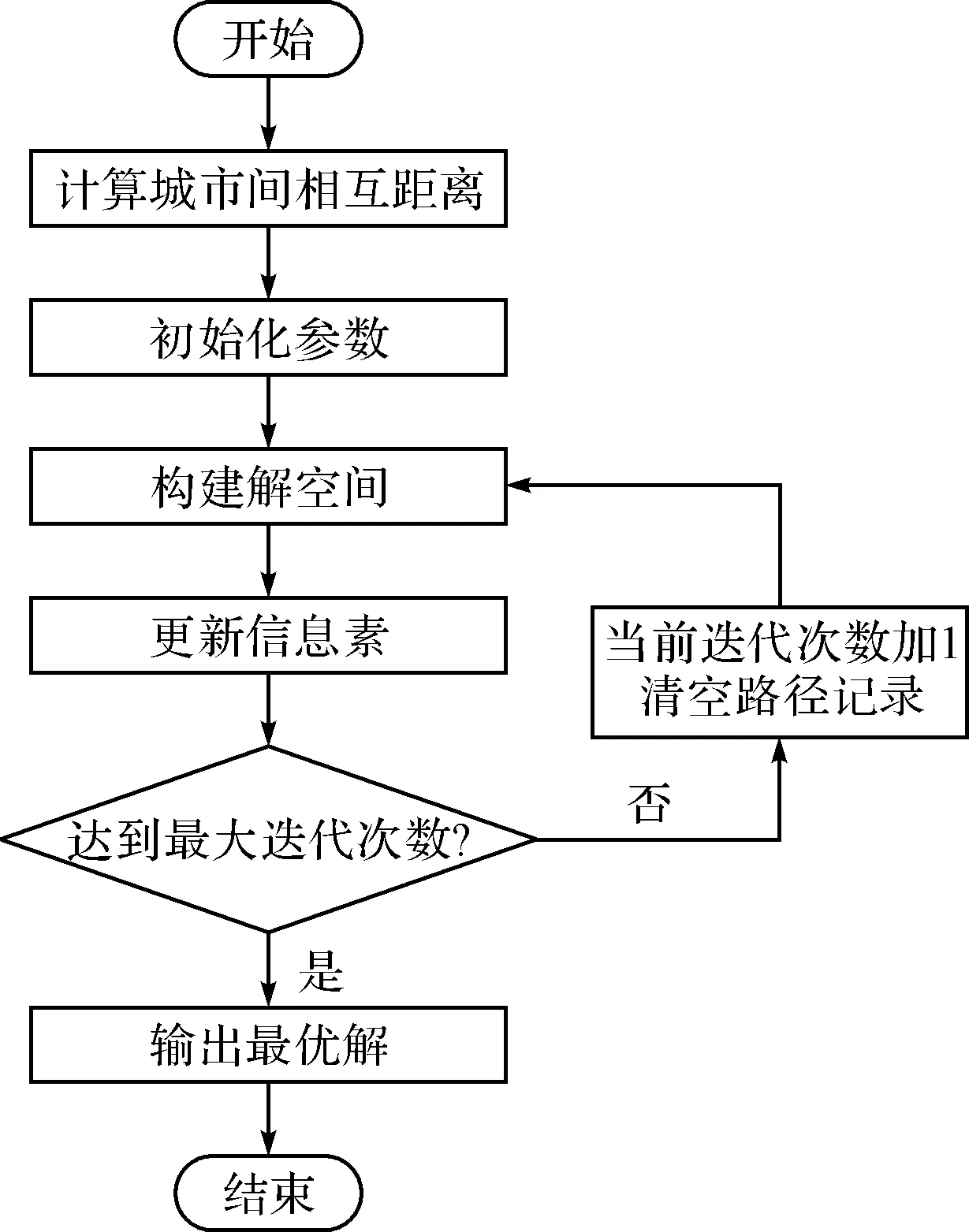
图1　蚁群算法解决CTSP问题基本步骤流程图

4) 更新信息素:计算各个蚂蚁经过的路径长度Lk(k=1,2,…,m),记录当前迭代次数中的最优解。同时根据式(2)和式(3)对各个城市连接路径上的信息素浓度进行更新。

5) 判断是否终止:若iter

3参数设置分析

3.1参数设置对其性能的影响

在蚁群算法中,蚂蚁数目m、信息启发式因子α、期望启发式因子β、信息素挥发因子ρ、信息素强度Q等参数的设置及不同的组合,都会对蚁群算法的求解性能、计算效率和结果的精度产生影响。蚁群算法的参数空间范围很大,而且各参数之间的关联性复杂,没有明确的规律可寻,因此找到最优的参数组合,使蚁群算法的稳定性、收敛性、正反馈性等性能达到最佳,使算法的计算结果达到最优,这是一个极其困难的问题,也是蚁群算法研究的重要部分[5]。

1) 蚂蚁数目对算法性能的影响

蚁群算法具有并行性的特点,即每个蚂蚁可以按照自己的规则在同一时刻内同时行动,所以当蚂蚁数目增多时,蚁群算法的全局搜索能力及稳定性会增强,但当蚂蚁的数目继续增加到某个值后,之前被搜索过的路径上的信息素浓度变化将会趋于某个定值,信息的正反馈作用减小,算法的收敛速度变慢;反之,当蚂蚁数目减小时,算法搜索的随机性会降低,此时虽然收敛速度加快,但也降低了算法的全局收敛性能,算法的稳定性变差,算法运行结果会出现过早停滞现象[6]。

2) 启发式因子对算法性能的影响

在蚂蚁的运动过程中,启发式因子α反映路径上累积的信息素浓度在蚁群搜索机制中的相对重要程度,它的值越大,则蚂蚁选择之前走过的路径的概率越大,这就会减弱蚁群搜索的随机性;反之,当启发式因子α值过小时,则容易使蚁群的路径搜索过早陷入局部最优解,最终可能找到的这条路径并非是最优路径[7]。

3) 期望启发因子对算法性能的影响

在引导蚁群搜索的过程中,期望启发因子β代表启发式信息的相对重要程度。在整个蚁群寻优过程中,β的大小反映了算法的先验性和确定性因素这二者的作用强度,β越大,在某个局部点上蚂蚁选择局部最短路径的概率越大,算法更容易陷入局部最优,从而收敛到一些并不高明的解上。

4) 信息素挥发因子对算法性能的影响

信息素挥发因子ρ表示信息素的挥发程度,它的取值直接影响到蚁群算法的全局搜索能力和收敛速度。当ρ较大时,之前搜索过的路径再次被选择的可能性增大,这对算法的随机性和全局搜索能力都产生不利影响。而当ρ较小时对算法的影响具有两面性,一方面,未被搜索过的路径上的信息量将迅速减少,减小了算法的搜索空间,使算法容易陷入局部最优解;另一方面,之前被搜索路径上的信息素增量减小,这使得搜索空间增大,算法陷入局部最优的概率减小,同时降低了算法的收敛性[8]。

5) 信息素强度对算法性能的影响

在Ant Cycle System模型中,信息素强度用Q表示,它反映了蚂蚁沿路径循环一周释放的信息素总量。当Q的值越大,算法的收敛性会越高,同时由于反馈性加强,使得蚂蚁的搜索空间减小,算法陷入局部最优的概率也会增大。

3.2参数设置对求解精度的影响

目前关于蚁群算法的参数设置,理论成果较为稀少,主要是靠经验和实验来设定的[9]。蚁群算法中Ant Cycle System模型应用最多,以此为例,其参数设定最好的经验结果为0≤α≤5;0≤β≤5;0.1≤ρ≤0.99;10≤Q≤10000[10]。此时给出的参数建议只是一个范围,为了获得最优求解结果,仍然需要在各个参数的建议取值范围内为每个参数设定确定的值。

在CTSP问题中,通常人们采用的策略是先确定参数重要性,然后按照重要性次序依次让一个参数变化,其他参数固定的方法来对参数进行选择[11～12],这种方法忽略了参数之间的耦合,求解出的最优路径长度不能保证是最短路径,如文献[4]的最优结果是15601.9195。

为了消除各个参数之间可能存在的非独立耦合关系,本文尝试采用循环组合的枚举方式进行最优结果求解,即在蚁群算法解决CTSP的基础上,按照5≤m≤50,0≤α≤5,0≤β≤5,0.1≤ρ≤0.5,1≤Q≤10000由外到里的顺序逐层循环嵌套。通过做大量的参数循环计算,本文找到了比文献[4]更优的CTSP路径。表1是本文方法某次循环执行获得的最好计算结果以及对应的参数设置、迭代次数和最短路径。从该表中可以发现,在该组参数的设定下,不仅取得了更优的结果,而且迭代次数也更少一些,算法的收敛速度更快。

表1　测试结果比较

图2中可以清晰看到,本文方法所得到的最优路径的距离更短。图3可以发现随着迭代次数的增加,最短距离与平均距离均呈不断下降的趋势,直到最短距离不再变化时,说明已找到最优路径。而本文方法达到最佳路径时的迭代次数也相对少一些。

图2　本文方法与文献[4]方法获取的最优化路径对比

图3　本文方法和文献[4]方法的各代最短距离与平均距离对比

通过对比可见,参数的设置对于路径的长度和迭代次数都会产生重要影响,只让一个参数变化,其他参数固定的策略对参数进行选择,显然还不够合理,通过多层循环嵌套能够得出最优化的结果。

4结语

蚁群算法的参数设置通常都是根据经验或实验反复试凑,或者通过让一个参数变化,另外几个参数固定不变的方法来选择参数,这显然无法使蚁群算法的收敛性和计算效率达到最优。在蚁群算法解决CTSP问题的过程中,本文对参数的设置进行实验分析,从蚁群算法参数之间的非独立性出发,通过多层循环策略找到了一个更优化的结果,

为蚁群算法求解TSP问题相关研究提供了参考。当然,本文方法运算量较大,如何在保证计算精度的前提下减小运算量是后续研究的重点。

参 考 文 献

[1] Colorni A, Dorigo M, Maniezzo V, et al. Distributed optimization by ant colonies[C]//Dorigo M. Proceedings of the 1st European Conference on Artificial Life. Paris: Elsevier Publishing,1991:134-42.

[2] Dorigo M, Maniezzo V, Colorni A. Ant system: optimization by a colony of cooperating agents[J]. IEEE Transaction on Systems, Man, and Cybernetics-Part B,1996,26(1):29-41.

[3] 郭倩倩.蚁群算法的改进及其在车辆路径问题中的应用[D].成都:西南交通大学,2007:9-11.

GUO Qianqian. Improvement of Ant Colony Algorithm and Its Application in Vehicle Routing Problem[D]. Chengdu: Southwest Jiaotong University,2007:9-11.

[4] 史峰,王辉,郁磊,等.智能算法30个案例分析[M].北京:北京航空航天大学出版社,2011:206-215.

SHI Feng, WANG Hui, YU Lei, et al. 30 Case Analysis of Intelligent Algorithm[M]. Beijing: Beihang University Press,2011:206-215.

[5] 王军.蚁群算法求解TSP时参数设置的研究[J].科学技术与工程,2007,7(17):4501-4503.

WANG Jun. Study on the Parameter Setting of TSP with Ant Colony Algorithm[J]. Science, Technology and Engineering,2007,7(17):4501-4503.

[6] 叶志伟,郑肇葆.蚁群算法中参数α、β、ρ设置的研究——以TSP问题为例[J].武汉大学学报,2004,29(7):597-600.

YE Zhiwei, ZHENG Zhaobao. Setting Parameter Research of α、β、ρ in Ant Colony Algorithm — Take the TSP Problem as an Example[J]. Journal of Wuhan University,2004,29(7):597-600.

[7] 徐红梅,陈义保,刘加光,等.蚁群算法中参数设置的研究[J].山东理工大学学报,2008,22(1):7-11.

XU Hongmei, CHEN Yibao, LIU Jiaguang, et al. Study on Parameter Setting in Ant Colony Algorithm[J]. Journal of Shandong University of Technology,2008,22(1):7-11.

[8] 杜衡吉,李勇.蚁群算法中参数设置对其性能影响的研究[J].现代计算机,2012,5:3-7.

DU Jiheng, LI Yong. Study on the Effect of Parameter Setting on the Performance of Ant Colony Algorithm[J]. Modern Computer,2012,5:3-7.

[9] 李敏,吴浪,张开碧.求解旅行商问题的几种算法的比较研究[J].重庆邮电大学学报,2008,20(5):624-626.

LI Min, WU Lang, ZHANG Kaibi. Comparison of Several Algorithms for Solving Traveling Salesman Problem[J]. Journal of Chongqing University of Posts and Telecommunications,2008,20(5):624-626.

[10] 段海滨.蚁群算法原理及其应用[M].北京:科学出版社,2005:100-114.

DUAN Haibin. Principle and Application of Ant Colony Algorithm[M]. Beijing: Science Press,2005:100-114.

[11] 李明海,邢桂华.用Matlab实现中国旅行商问题的求解[J].微计算机应用,2004,25(2):218-222.

LI Minghai, XING Guihua. Solving the Problem of Chinese Traveling Salesman with MATLAB[J]. Micro Computer Application,2004,25(2):218-222.

[12] 燕忠,袁春伟.用蚁群优化算法求解中国旅行商问题[J].电路与系统学报,2004,9(3):122-126.

YAN Zhong, YUAN Chunwei. Solving the Chinese Traveling Salesman Problem with Ant Colony Optimization Algorithm[J]. Journal of Circuits and Systems,2004,9(3):122-126.

Parameters Setting of Ant Colony Algorithm for CTSP Problem

YANG Hui1HAN Litao1,2LEI Yanhui1ZHENG Ying3WU Jiayi1

(1. Geomatics College, Shandong University of Science and Technology, Qingdao266590)(2. Key Laboratory of Surveying and Mapping Technology on Island and Reed, SBSM, Qingdao266590)(3. Hebei Institute of Civil Engineering, Zhangjiakou075000)

AbstractThere are many parameters in the ant colony algorithm, and setting of different parameter values has a great influence on the calculation results. At present adequate theoretical basis is short in terms of parameter setting. In this paper, the basic principle of ant colony algorithm and the solution of CTSP problem are introduced in detail. It also emphatically discusses and analyzes the influence of various parameters on ant colony algorithm and setting the rational parameters. The enumerate method of parametric loop combination is used to solve the CTSP problem and a better result is obtained.

Key Wordsant colony algorithm, CTSP, parameter setting

* 收稿日期:2015年11月7日,修回日期:2015年12月24日

基金项目:国家自然科学基金项目(编号:41201381);山东省“泰山学者”建设工程专项经费项目资助。

作者简介:杨惠,女,硕士研究生,研究方向:地理信息系统应用与研发。韩李涛,男,博士,副教授,硕士生导师,研究方向:海洋测绘、路径规划。类延辉,女,硕士研究生,研究方向:室内定位。郑莹,女,硕士,讲师,研究方向:制图综合。吴佳怡,女,硕士研究生,研究方向:室内GIS。

中图分类号TP301.6

DOI:10.3969/j.issn.1672-9722.2016.05.003