克隆植物的演化博弈研究
2016-06-20韩定定李德志
杜 莎,韩定定,李德志
(华东师范大学信息科学技术学院,上海 200241)
克隆植物的演化博弈研究
杜莎,韩定定,李德志
(华东师范大学信息科学技术学院,上海 200241)

摘要:基于复杂网络理论构建包含等级生长单位的互花米草克隆植株多重关系网络,分析该网络结构,获取了互花米草的生长特征及其株丛间彼此回避竞争的生态学策略。将囚徒困境演化博弈模型引入互花米草克隆植株多重关系网络,通过对网络上演化博弈现象的刻画,展现了按照不同的规则选取网络中的合作节点时网络的特征:随机均匀选取初始合作节点时,合作频率随着背叛诱惑值的增加逐渐下降;选择不同类型的生物体单位为初始合作节点,选取株丛间根状茎间隔点,演化博弈到达稳态时,合作者的比例随着背叛诱惑值的增加而逐渐减小,这意味着根状茎节点为互花米草生长的关键节点。
关键词:克隆植物;多重关系网络;演化博弈模型;囚徒困境
0引言
网络上的演化博弈是复杂系统中基本的动力学行为之一。在诸多相关的演化博弈模型研究中,囚徒困境博弈模型是最具代表性的问题之一,而已有的囚徒困境演化博弈研究通常在初始时刻随机均匀选择合作节点,难以反映真实网络中合作节点和背叛节点不均匀分配的现实映射意义:一方面,网络本身的拓扑结构决定了网络的合作水平;另一方面,网络中初始时刻合作节点的选择机制会影响整个演化博弈动力学过程。
演化博弈中的合作行为在生物进化历史中起到了关键的作用,可自我复制的细胞通过合作形成了多细胞生物;动物以家庭为合作单位进行捕食以繁衍自己的后代。科学家们对演化博弈的初始研究通常在0维系统中进行,在该系统中每个个体之间都可以进行博弈。随着研究发展,科学家们将演化博弈引入了正则格子网络中,正则格子是指网络中的每个节点都具有相同的度,这意味着网络中的所有个体每轮博弈都与相同数目的邻居进行交互作用。Nowak和May[1]首先将空间结构引入博弈模型,对二维方格格子上的囚徒困境博弈进行了研究。Nowak等认为,受空间结构限制的个体进行博弈的范围有限,有助于形成紧密的合作团簇,有效地促进了合作行为的涌现。Szabó[2-4]等对相同网络度的不同规则格子上的囚徒困境行为进行了研究。小世界网络[5-6]上的博弈研究同样得到了广泛的关注。Wu等[7]考虑到现实生活中个体的不同影响力,提出了一个描述个体影响力演化的动态优先选择博弈模型。Santos等[8]发现,由于重连使得网络变得异质,所以WS小世界网络能够通过这一方式有效提高合作涌现的程度。Kim等[9]认为是小世界网络中的长程连接导致了演化博弈合作的突然崩溃。近年来,统计研究表明,大量真实网络表现出“富者愈富”的现象,满足无标度特性,BA无标度网络模型应运而生[10],这又为研究指明了新的方向。无标度网络上的演化博弈研究也成为了科学家们研究的热点,Santos等[11-13]研究了度不相关的BA无标度网络上的两人两策略博弈行为,结果表明,无标度网络结构无论在囚徒困境博弈还是在雪堆博弈上都能够极大地促进合作,合作的强度对于种群的规模具有鲁棒性。Rong Z H等[14-15]讨论了度相关性与网络演化博弈行为之间的相互影响。这些研究揭示了网络的不同结构特性对博弈行为的影响。
然而,生态系统是一个复杂体系,克隆植物[16-17]的分布特点反映了植株等级生长单位演化博弈策略的不同选择。互花米草是一种典型的克隆植物,原产于美洲大西洋沿岸的多年生禾本科米草属植物,通过无性生殖过程进行繁衍,因其促淤造陆和消浪护堤作用显著而被引入东滩湿地。但随着互花米草的不断繁衍扩散,并不断排挤本地植物海三棱藨草和芦苇等[18],逐渐占领了东滩东部与北部的整个低潮位与大部分中潮位。与此同时,人工的大面积围垦造成高潮位的部分植被逐渐消失,尤其是与互花米草具有相当竞争力的本地种芦苇,人为因素对其扩散和繁衍起到了严重的干扰作用。在这种背景下,互花米草在几十年的时间内,就成为了入侵东滩的有害植物,对崇明当地的生物多样性以及生态系统平衡产生了严重的影响。
本文构建了克隆植株互花米草树状网络结构,同时引入了囚徒困境演化博弈模型进行探究,实证研究互花米草克隆植株树状结构网络的演化博弈和生长特征,对其博弈生长状况进行探究,并且获取了一种新型的分析区域生境异质性的方法。
1互花米草克隆植株多重关系网络及其特征
依据野外获取的3个互花米草基株空间构型的连接情况,考虑互花米草实际的生长特点,采用复杂网络构网方法构建3个包含等级生长单位的互花米草克隆植株多重关系网络:株丛作为A类节点,分株作为B类节点,株丛间根状茎间隔点作为C类节点,抽穗分株作为D类节点。
图1所示为3个互花米草克隆植株多重关系网络的度分布,在双对数坐标下,可以明显看出,网络中的节点大多聚集在度值较低的区域,在度值较大的区域,节点的度分布呈现近似幂律分布关系。3个网络的幂指数分别近似为1.64,1.42,1.68。在互花米草克隆植株多重关系网络中,度值小于10的节点大多为根状茎间隔节点和抽穗分株节点,度值较大的节点为株丛和分株节点。由度值分布可以看出,互花米草克隆植株多重关系网络中存在着大量的根状茎间隔节点和抽穗分株节点,只存在少数具有大量分枝的株丛和分株节点。

图1 互花米草克隆植株多重关系网络的度分布
对互花米草克隆植株多重关系网络的临近节点平均度knn(k)进行分析,其与度值k的关系在双对数坐标下如图2所示。从图2中可以看出,在度值k较小的时候,knn(k)随度值k的增加而逐渐衰减,而在度值k逐渐增大的时候,空间地理因素变强后,网络变得同质,度负相关的现象逐渐消失,出现较为平坦的区域,此时knn(k)几乎是一个常数,表示网络没有度相关性,甚至在某些度值区域,knn(k)随k的增加略微上扬。这种略带度正相关的拓扑可能是由于“空间集团效应”[19]造成的。由于强大的地理限制,导致节点优先连接自己空间上的近邻,某些分布较为密集的节点群就会互相连接,从而在某个空间区域中形成集团,进而导致度正相关。这说明互花米草克隆植株在崇明东滩湿地,生境资源不够丰富,环境对互花米草分株的生长连接调控作用不强,因此,互花米草分株的生长连接多由自身调节控制。在某些局部范围内,由于互花米草网络呈现同配性,因此,网络格局呈现斑块化空间集团效应。

图2 互花米草克隆植株多重关系网络的临近节点平均度
2互花米草克隆植株网络上的囚徒困境演化博弈
在经典囚徒困境博弈(Prisoner’s dilemma, PD)模型中,考虑两个小偷合伙作案,被捕后隔离审讯。他们都知道,如果双方都坦白交代罪行,那么两人都将获刑3年;而如果双方都拒绝坦白,那么两人都将获刑2年。但是,如果一方坦白,而另一方拒不认罪,则坦白者将获刑1年,拒不认罪者将获刑5年。囚徒困境博弈的收益可以表示为矩阵(1):
CD
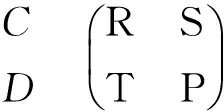
(1)
可以看出,囚徒困境博弈中涉及两个人和两种策略,它的策略组合包括:1)双方都选择合作,记为(C,C)。每个人的收益为“对双方合作的奖励”R;2)如果一方合作而另一方背叛,记为(C,D)或(D,C)。背叛者会获得“背叛的诱惑”T,而合作者得到“傻瓜的报酬”S;3)如果双方都选择背叛,记为(D,D),则每个人的收益记为P,即“对双方都背叛的惩罚”。
在囚徒困境博弈中,对于前面的例子,有R=-2,S=-5,T=-1,P=-3,即T>R>P>S,由此可以看出,如果两个个体仅进行一轮囚徒困境博弈,如果将他们作为一个整体,他们能够获得的共同最大收益是共同选择合作的策略;然而对于每个参与者来说,无论对方使用什么样的策略,选择坦白总是能够获得更大的收益。囚徒困境博弈模型在生物学和人类学都有广泛的研究,可以用来解释吸血蝙蝠之间的反哺[20]、运动员服用兴奋剂以及国家间的军备竞赛等许多现象。
在互花米草克隆植株多重关系网络中,不同的生长单位在每一轮演化博弈中具有不同的策略,选择合作策略的个体由于光合作用和吸收作用产生生长所需的大量物质,传输给选择背叛策略的个体,促进背叛个体的生长。
本文采用一种随机策略更新演化规则——费米规则:假设在每一轮博弈中,个体x会随机选择一个邻居y,并比较二者的本轮收益;在下一轮博弈中x采取y本轮策略的概率根据统计物理中的费米函数进行计算:
(2)
其中,Sx为x本轮采取的策略,Px为x本轮收益。κ描述了环境的噪声因素,反映了个体在策略更新时的不确定性。如图3所示,当0<κ<<1,如果本轮个体x的收益Px小于个体y的收益Py时,则x将一定会学习y的策略;当κ>0.1时,如果本轮个体x的收益Px小于个体y的收益Py时,则x将以一定的概率接受y的策略;当κ>>1时,则表示个体处于噪声环境中,无法做出理性决策,只能随机更新自己的策略。

图3 不同噪声值(κ)下,费米函数同个体x和个体y的收益差(Px-Py)之间的关系
复杂网络上的演化博弈主要包括两个步骤:1)网络中的所有参与者同时和其网络上直接相连的邻居进行博弈,并获取收益。在进行博弈的过程中,每个参与者的收益为其与所有邻居发生博弈得到收益的总和;2)参与者将他本轮博弈的收益与其网络上直接相连的邻居的收益进行比较,并按照一定规则更新自己的策略。
3互花米草克隆植株多重关系网络的不同策略选择
已有的囚徒困境演化博弈研究通常在初始时刻随机均匀选择合作节点,难以反映真实网络中合作节点和背叛节点不均匀分配的现实映射意义:一方面,网络本身的拓扑结构决定了网络的合作水平;另一方面,网络中初始时刻合作节点的选择机制会影响整个演化博弈动力学过程。因此本文在互花米草克隆植株多重关系网络中引入囚徒困境演化博弈模型,分别在演化博弈的初始时刻,网络中的合作节点选取遵循两种不同的规则:随机选择初始策略和按照节点类型选取初始策略。
3.1随机选择初始策略
初始时,为网络中的个体随机均匀分配合作或背叛策略,分析演化博弈到达稳态时刻互花米草克隆植株网络中合作者的比例。合作频率fc和背叛诱惑值b的关系如图4所示,该图是20次模拟仿真的平均结果。可以看出,当背叛者相对于合作者优势较小时(如b=1.05),网络上各节点间将以较高频率进行合作。随着b的增大,背叛者相对于合作者的优势增加,互花米草克隆植株网络会由合作是网络的主要特征(fc>0.5)转变为背叛为网络的主要特征(0 图4 在κ=0.1的噪声环境下,随机选择初始节点策略时,互花米草克隆植株多重关系网络中合作频率(fc)和背叛诱惑值(b)之间的关系 然而仔细观察可以发现,随着背叛诱惑值b的增加,合作频率fc并不是一直下降的,而是在到达一定程度后基本保持不变,也就是说,互花米草可能可以通过内在的某种机制,使网络中合作者保持在一定的水平,以此来给予新加入的节点(即新长出来的节点)生长所需要的资源或能量。这也说明了随着演化博弈的进行,网络中背叛个体逐渐增加,网络中节点所获取的资源都用于维持自身的生长和繁衍,越来越多的个体选择从环境中获取资源或能量,而非从邻近节点中获取。 图5显示了互花米草种群合作频率随时间的演化过程,该图是20次模拟仿真的平均结果。经过一段长期暂态过渡过程(如102步或更短时间),合作者的比例逐渐稳定。这说明当互花米草网络经过一段长期的演化博弈过程后,最终会达到一个稳定的状态,此时网络中的个体策略基本保持不变。同时,可以看出,在互花米草多重关系网络中,对于不同的背叛诱惑值b,网络中合作者的比例fc趋向的稳定值也不相同:随着b值的增加,背叛者相对于合作者优势增加,网络中合作频率逐渐下降,且网络到达稳态所需时间越短,博弈个体做出决策的过程越短。 图5 在κ=0.1的噪声环境下,随机选择初始节点策略时,合作频率(fc)随时间(t)的演化 对互花米草克隆植株多重关系网络上背叛行为的扩散过程进行分析,可以阐述中心节点对背叛者入侵的抵抗能力。假设初始时刻互花米草克隆植株网络中度值最大的节点为背叛者,其余节点都选择合作策略,仿真结果(见图6)说明了取不同的背叛诱惑值b时,网络中合作节点的比例fc随时间的变化情况。图6是20次模拟仿真的平均结果。可以发现,在互花米草克隆植株网络中,随着背叛诱惑值b的增大,背叛者相对于合作者的优势增加,网络的合作频率fc也逐渐衰减,同时,仔细观察可以看出,网络演化博弈到达稳态所需的时间越短。在互花米草克隆植株的生长过程中,如果度值最大的株丛节点成为背叛节点,则不能自主生长的分株、抽穗分株都不能从该株丛中获取资源或物质,这些节点所拥有的资源和物质仅能供自身生长所需,不仅不能“帮助”其他节点进行生长,还会对其他株丛节点进行“剥削”,因此网络中合作水平较低。 图6 在κ=0.1的噪声环境下,互花米草克隆植株网络上背叛的中心节点对网络合作行为的入侵性 如图7显示了互花米草克隆植株多重关系网络中,引入囚徒困境演化博弈前后网络的策略分布,尽管初始时刻策略随机均匀分布,有部分度值较小的节点采取合作策略,但到了稳定状态,这些节点会转变为背叛者;同时,仔细观察可以看出,度值较大的节点策略基本保持不变。这说明互花米草多重关系网络中小度节点的合作行为是不稳定的,但度值较大的节点在演化博弈过程中可以较好地保持自己的策略。 在互花米草的真实生境中,度值较大的节点一般生境资源丰富,对互花米草的生长起到较好的促进作用,能够较好地保持自己的策略,度值较小的节点所在生境调控作用较弱,资源丰富程度不够,此时,互花米草分株的生长连接多由自身调节控制,受环境影响不大。这也说明,新长出的株丛,并非倾向于最佳的资源丰富的生长环境,而是寻求次佳生境进行繁衍,体现了互花米草株丛间回避竞争的内在机制。 3.2根据节点类型选择初始策略 在互花米草克隆植株多重关系网络中引入囚徒困境演化博弈,株丛作为A类节点,分株作为B类节点,株丛间根状茎间隔点作为C类节点,抽穗分株作为D类节点。初始时刻选择不同类型的节点作为合作者,得到演化博弈到达稳态时网络中合作者的比例fc如图8所示。由图8可以明显看出,当分别选取A,B和D类节点初始时刻为合作节点时,即使演化博弈中背叛诱惑值b很小,背叛者对于合作者的优势不明显时,网络中的合作频率b仍为0。而当选取C类节点,即株丛间根状茎间隔点在初始时刻作为合作节点时,如果取较小的背叛诱惑值b(b<1.3),演化博弈到达稳态时,合作者的比例fc不为0,并且fc随着b的增加而逐渐减小,合作者湮灭的阈值b≈1.3,即当b>1.3时,网络中合作频率fc均为0。 开始演化时(a,b,c)网络中具有相同数目的合作者(C,蓝色柱状图)和背叛者(D,红色柱状图)。囚徒困境演化后的稳定状态(d,e,f)。每个节点度的柱状图之和为1,蓝色和红色所表示的分数为每个度值中不同策略所占的相对百分比。κ=0.1的噪声环境,背叛诱惑值b=1.3。 初始时刻选取C类节点,即株丛间根状茎间隔点为合作节点,b<1.3时,演化博弈到达稳态时,合作者的比例fc不为0。该图是20次模拟仿真的平均结果。在κ=0.1的噪声环境下,演化博弈开始时,选择不同类型节点作为合作节点。 从互花米草克隆植株的角度来说,当根状茎节点初始时刻作为合作节点时,网络演化博弈的过程中,背叛诱惑值b超出一定的范围后,会引起互花米草克隆植物网络整体动力学特征的变化。当互花米草基株的根状茎不再为株丛、分株或抽穗节点传递养分后,整个基株可能会分散生长或者停止株丛之间的资源、信息交互。 4结论 本文基于在崇明东滩获取的互花米草克隆植株空间构型,选择互花米草克隆植株作为树状网络的实证研究对象,构建互花米草克隆植株多重关系网络,研究其相关拓扑和度分布关系,分析其演化博弈现象。首先,分析树状网络拓扑结构,获取了互花米草的生长特征及其株丛间彼此回避竞争的生态学策略。其次,在互花米草树状网络中,引入了囚徒困境演化博弈模型,初始时刻,分别按照两种不同的规则选取网络中的合作节点:第一种是随机均匀选取合作节点,随着背叛诱惑值b的增加,合作频率fc逐渐下降;第二种是选择不同类型的生物体单位为合作节点,当分别选取A、B和D类节点初始时刻为合作节点时,即使演化博弈中背叛诱惑值b很小,网络中的合作频率fc均为0,而当选取C类节点,取较小的背叛诱惑值b时(b<1.3),演化博弈到达稳态时,合作者的比例fc随着b的增加而逐渐减小,合作者湮灭的阈值b≈1.3。两种不同策略的选取,意味着根状茎节点为互花米草生长的关键节点。经过构建互花米草克隆植株树状网络,对网络的拓扑结构和动力学演化博弈进行了分析,得到了互花米草克隆植株网络自身的生态学特性和株丛间彼此回避竞争的生态学策略,这一发现具有重要的生态学意义。 参考文献: [1]Nowak M A, May R. Evolutionary games and spatial chaos[J]. Nature, 1992, 359(6398): 826-829. [2]Szabó G, Fath G. Evolutionary games on graphs[J]. Phys Reports, 2007,446(4/5/6): 97-216. [3]Szabó G, Toke C. Evolutionary prisioner’s dilemma game on a square lattice[J]. Phys Rev E, 1998,58(1): 69-73. [4]Vukov J, Szabó G, Szolnoki A. Cooperation in the noisy case: prisioner’s dilemma game on two types of regular random graphs[J]. Phys Rev E, 2006, 73(6): 067103. [5]Watts D J, Strogatz S H. Collective dynamics of 'small-world' networks.[J]. Nature, 1998, 393(6684): 440-442. [6]Newman M E J, Watts D J. Renormalization group analysis of the small-world network model[J]. Physics Letter A, 1999, 263(4): 341-346. [7]Wu Z X, Xu X J, Huang Z G, et al. Evolutionary prisoner’s dilemma game with dynamic preferential selection [J]. Physical Review E, 2006, 74(2): 021107. [8]Santos F C, Rodrigues J F, Pacheco J M. Epidemic spreading and cooperation dynamics on homogeneous small-world networks[J]. Physical Review E, 2005, 72(5): 056128. [9]Kim B J, Trusina A, Holme P, et al. Dynamic instabilities induced by asymmetric influence: prisoners’ dilemma game in small-world networks[J]. Physical Review E, 2002, 66(2): 021907. [10] Barabási A L, Albert R. Emergence of scaling in random networks[J]. Science, 1999, 286(5439): 509-512. [11] Santos F C, Pacheco J M. Scale-free networks provide a unifying framework for the emergence of cooperation [J]. Physical Review Letters, 2005, 95(9): 098104. [12] Wu Z X, Xu X J, Huang Z G, et al. Evolutionary prisoner’s dilemma game with dynamic preferential selection [J]. Physical Review E, 2006, 74(2): 021107. [13] Santos F C, Pacheco J M, Lenaerts T. Evolutionary dynamics of social dilemmas in structured heterogeneous populations[J]. Proceedings of the National Academy of Sciences of the United States of America, 2006, 103(9): 3490-3494. [14] Rong Z, Li X, Wang X F. Roles of mixing patterns in cooperation on a scale-free networked games[J]. Physical Review E, 2007, 76(2): 027101. [15] Rong Z, Yang H X, Wang W X. Feedback reciprocity mechanism promotes the cooperation of highly clustered scale-free networks[J]. Physical Review E, 2010, 82(4): 047101. [16] Grace J B. The adaptive significance of clonal reproduction in angiosperms: an aquatic perspective[J]. Aquatic Botany, 1993, 44(2): 159-180. [17] Ellstrand N C, Roose M L. Patterns of genotypic diversity in clonal plant species[J]. American Journal of Botany, 1987, 74(1): 123-131. [18] 王卿. 互花米草在上海崇明东滩的入侵历史、分布现状和扩张趋势的预测[J]. 长江流域资源与环境, 2011, 20(6): 690-696. Wang Qing. Spartaina alterniflora invasion in chongming dongtan, Shanghai: history, status and prediction[J]. Resources and Environment in the Yangtze Basin, 2011, 20(6): 690-696. [19] 陈希, 钱江海, 韩定定. L空间和P空间模型下的树状结构网络[J]. 计算机应用研究, 2015, (1):45-47. Chen Xi, Qian Jianghai, Han Dingding. Tree network under space L and space P model[J]. Application Research of Computers, 2015, (1):45-47. [20] Wilkinson G S. Reciprocal food sharing in the vampire bat[J]. Nature, 1984, 308(5955): 181. (责任编辑李进) The Evolutionary Game Study on a Clonal Plant Spartina Alterniflora Loisel DU Sha, HAN Dingding, LI Dezhi (East China Normal University, Shanghai 200241, China) Abstract:This paper constructs the empirical network of the clonal plant multiple relation treelike networks based on the spatial configuration of Spartina alterniflora to explore the evolutionary game characteristics. First, we study the structure properties of Spartina alterniflora, which reflect the ecological strategy that avoiding competition between each other. Second, the model of the evolutionary Prisoner’s Dilemma game is introduced into the Spartina alterniflora treelike network. Initially, the distribution of strategies among the nodes in the network obeys two different rules: distributed randomly, with fc decreasing with the increasing of b, in accordance with different types of Spartina alterniflora biological units, the rhizome nodes between the neighboring bunches play an important role. Key words:clonal plants; multiple relation network; evolutionary game theory; prisoner's dilemma game 文章编号:16723813(2016)01009507; DOI:10.13306/j.1672-3813.2016.01.010 收稿日期:2015-07-09 基金项目:国家自然科学基金(11075057) 作者简介:杜莎(1989-),女,四川自贡人,硕士研究生,主要研究方向为复杂网络与智能化信息处理。 中图分类号:TP393 文献标识码:A




