复杂网络上疫情与舆情的传播及其基于免疫的控制策略
2016-06-20尚明生
刘 影,王 伟,尚明生,唐 明
(1. 电子科技大学互联科学中心, 成都 611731;2. 西南石油大学计算机科学学院,成都 610500)
复杂网络上疫情与舆情的传播及其基于免疫的控制策略
刘影1,2,王伟1,尚明生1,唐明1
(1. 电子科技大学互联科学中心, 成都 611731;2. 西南石油大学计算机科学学院,成都 610500)

摘要:较为全面的综述复杂网络的免疫问题,包括:真实疫情和舆情传播场景的抽象与建模、疾病传播模型、全局免疫策略和局域免疫策略等。在若干真实网络和模型网络上模拟免疫控制的结果表明,基于中心性、图划分、熟人免疫等策略的免疫效果比随机免疫好,这说明免疫策略的选择对传播控制具有实际指导意义。在选择免疫策略时,应考虑网络的拓扑结构特性和信息的完整程度,才能达到较佳控制效果。
关键词:复杂网络;传播动力学;疫情与舆情; 网络免疫
0引言
当前,有效应对和处理公共突发事件已经成为维护国家安全和社会稳定的一个重要研究课题和任务。所谓公共突发事件是指突然发生,可能造成重大人员伤亡、财产损失、生态环境破坏和严重的社会危害,危及公共安全的紧急突发事件。疫情是一种典型的突发公共卫生事件,指疾病的发生和快速蔓延,包括人类传染病、动物传染病和植物传染病。例如SARS、禽流感、H1N1流感、埃博拉病毒、熊猫烧香、震荡波等生物和计算机病毒,以社会网络和科技网络作为传播载体,在短时间内造成大范围的感染,具有传播速度快、破坏能力大的特点。随着互联网的广泛应用,计算机病毒传播更是令人关注的一种疫情形式。舆情是“舆论情况”的简称,是指在一定的社会空间内,围绕社会事件的发生、发展和变化,作为主体的民众对作为客体的社会管理者及其政治取向产生和持有的社会政治态度。同时,它也是群众对社会中各种现象、问题所表达的信念、态度、意见和情绪等表现的总和。借助互联网、手机短信、微博等新兴信息交互平台,意见表达和信息传播渠道变得非常广泛。当网络信息不对称,特别是人们对相关信息真伪的辨别能力有限时,信息可能演变成谣言在人群中快速传播[1-2]。如2008年汶川大地震后互联网上流传上游水库遭到污染的谣言使成都发生了疯狂的抢水事件。2011年日本核泄漏事故将导致食盐含有放射物质的谣言引发了抢盐风潮。网络舆情具有自发性、内容海量性、论点多样性、用户分散性等特点。及早发现和报告疫情和舆情,掌握它们在网络中的传播规律并对其进行有效的引导与管控,将大大减少这类突发事件给社会带来的不良影响和损失。
网络科学可以描述真实社会中的复杂系统,如人类接触网络、通讯网络、科学家合作网络、朋友关系网络等。网络中的节点代表个体或组织,边代表它们之间的交互关系,不同类型的网络都呈现出复杂的拓扑结构特性[3]。特别是1998年Watts和Strogatz发现网络具有小世界特性以及1999年Barabási和Albert发现网络具有无标度特性,对复杂网络的研究渗透到计算机、生物、管理等多个领域。疫情和舆情以各种网络为载体,以接触(物理接触和信息交流)的形式进行传播和扩散。疫情在人类及动物接触网络中的蔓延、计算机病毒在互联网上的传播、谣言在人群关系中的扩散都是符合某种规律的传播行为[4]。在社会交往和信息传递、交流中,网络个体之间通过长期的互动关系已经形成了相对稳定的社会网络,当疫情和舆情在接触网络、信息网络上传播时,受制于网络结构和传播规律从而具有一定的可预测性和可控制性。这为采用复杂网络的传播动力学方法分析传播规律,制定控制策略奠定了基础。复杂网络的传播动力学对传播的动态过程进行描述,建立能反映传播规律的动力学模型。通过对模型的定性分析和定量解析,揭示传播过程中的规律,如疾病爆发阈值、爆发时间、传播持续时间、传播最终的范围等[5]。由于疫情和舆情在传播内容、载体、接触模式上存在一定差异,传播机制也存在差异性。但是,网络内在的拓扑结构往往是决定传播范围的关键因素,在采用网络动力学机制研究疫情与舆情的传播控制时,现有方法都是采用传播模型模拟传播过程,在实施免疫策略后评估控制效果。免疫的核心思想是通过免疫目标对象切断其传播的途径,控制传播的扩散。采取免疫措施会产生大量的经济和安全方面的成本,人们总是希望在保持免疫数目较低的同时对传播有明显的抑制或控制效果。最佳的免疫策略应该是用最少的免疫量来最大限度地控制疫情和舆情的传播范围,这对于节约成本、挽救生命、维持社会稳定都具有非常重要的现实意义。
1真实社会中基于网络的传播场景
真实社会中存在大量以网络为载体的传播场景,如流行病在人类接触网络中的传播、计算机病毒在电子邮件网络中的传播、谣言在网络论坛上的传播等。有许多工作对真实社会传播场景进行建模和抽象。本节举例介绍了在线社交网络、社会接触网络、科技网络等几类网络上的传播场景。对真实场景的抽象建模是采用免疫理论实施舆情和疫情控制的基础。
1.1电子邮件网络上的病毒传播
人们的电子邮件往来构成了一个体现社会关系的网络。Newman等[6]构建了有向的邮件网络。在邮件网络中,每个节点代表一个用户账户。如果用户i出现在j的邮件列表中,则在节点i和j之间存在一条有向边。用户i出现在j的列表中,并不意味着用户j出现在用户i的列表中。电子邮件网络呈现出小世界特性,并且具有无标度的度分布。计算机病毒随着邮件的发送传播,其传播过程如下:用户定期的查看电子邮件,当遇到可能带病毒的邮件时,用户若打开病毒邮件,该节点就被感染并向邮件列表中的所有朋友发送病毒邮件。如果用户没有打开病毒邮件,则认为用户识别出病毒邮件并将其删除[7]。如果事先告知用户病毒特征,该节点就视作免疫,它不会转发病毒副本。
1.2网络论坛上的舆情传播
网络论坛是民众公开发表个人言论的公共区域,具有言论自由、开放、快速、互动等特点。Cao等[8]利用信息提取软件GooSeeker挖掘论坛中某一主题发表评论及回复的原始信息,对数据进行结构化处理,构建舆情传播模型。网民被赋予唯一的ID号,网民之间的回复关系形成有向边,有向边的数目为节点的出度和入度。根据回复次数还可以进一步将网络抽象成权重网络。通过网络拓扑结构寻找关键节点可以帮助定位网络论坛中的意见领袖,而监控及引导网络舆情中意见领袖的言论,对于舆情的演变和控制有着重要作用。
1.3接触网络上的疫情传播
禽流感是一种禽类间通过接触方式传染的动物疾病。Yang等[9]根据小世界网络的构建规则,建立了禽流感传播的网络模型。方法是:将发现病毒个体的方圆几十公里设为疫区,每个疫区看作网络中一个节点。考虑到禽流感病毒以接触传染为主,传播倾向于在局部相邻区域中展开,代表疫区的节点与左右相邻的节点相连形成环状的规则网络。病毒的远程传播只有在候鸟迁徙或者长途运输中会产生,这对应于将规则网络中的节点按照一定的概率建立远程连接。类似地分析疫情传播的工作还有模拟甲型H1N1流感的传播、非典的爆发、埃博拉病毒的传播等。
1.4互联网上的级联失效传播
因特网是世界上最大的计算机网络,对因特网结构的抽象主要基于路由器级别和自治域级别。前者把每个路由器看作节点,路由器之间的连接看作边。后者将自治系统(Autonomous System,AS)抽象为节点,AS之间的连接看作连边。当互联网上一个或多个节点由于恶意攻击或故障失效时,数据传输改变路径,故障节点的邻居节点由于负载突然变化可能引起级联失效效应,故障像病毒一样传播开。DIMES项目采集了互联网数据,分析发现因特网具有水母状的结构特性[10]。
此外,技术的革新、新产品的推广、新思想的采纳、行为的传播、科学论文的引用等社会现象,都可以抽象为复杂网络上的传播。虽然我们在此关注的是疫情与舆情的传播,但其相关策略可以推广到其它传播场景。
2传播模型
对免疫策略的研究,常常依赖于传播模型。通过模拟免疫策略实施前后传播影响范围的变化,设计和评估免疫策略。传播模型借助微分方程精确地刻画传播过程中节点状态的变化,能够精确预计传播时间、传播范围、传播阈值等。目前研究最深入、应用最广泛的传播模型是SIS(Susceptible-Infected-Susceptible)和SIR(Susceptible-Infected-Recovered)模型[11-12]。在这类传播模型中,个体可处于以下几种状态:易感态(Susceptible,个体当前处于健康状态,但能够被感染)、感染态(Infected,个体已经被感染,具有传染性)、恢复态(Recovered,个体曾经被感染但已获得免疫力,不会传播疾病,也不会再次被感染)。在研究舆情传播时,S态对应未听说过舆情信息的个体;I态对应舆情的传播者,他们已经接触到舆情并积极将舆情传播给邻居;R态对应已知舆情信息但并不传播舆情的人。这两个模型虽然简单,但也存在缺陷,即不能充分刻画传播过程中所有可能存在的状态。许多人类疾病如B型肝炎、艾滋病、登革热,病人都会经过一段潜伏期才会发病。在舆情传播中,某人听到舆情相关信息后,并不立即传播,而是通过一段时间的评估来决定是否接受并传播此信息。考虑到传播的延迟性和病毒的潜伏性,定义了节点的另一种状态暴露态(Exposed,也称作潜伏态)。处于潜伏态的节点以一定概率转化为感染态或健康态。
1)SIS模型。初始时,一小部分节点处于感染态I,其余节点处于易感态S。每一个时间步,I态节点接触它的一个随机选择的邻居(单点接触模式)或者全部邻居(全接触模式),并将S态邻居以概率α变为I态;感染完毕后I态节点以概率β恢复为S态,或者以概率1-β保持I态。网络的有效传播率为λ=α/β。传播过程在I态节点数目不变时达到稳定,此时I态节点密度为I*。SIS模型可模拟流感、肺结核等疾病的传播,患病病人在治愈以后并不能获得免疫力而是再次成为易感人群。受病毒入侵的计算机在清除病毒以后,也可能再次被感染。
2)SIR模型。每一个时间步,I态节点接触它的邻居,并将S态邻居以概率α变为I态。I态节点在感染了S态节点之后,以概率β变为R态,或者以概率1-β保持I态。传播过程直到网络中没有I态节点为止,此时R态节点的比例为R*。R*越大,说明传播影响力越大。像麻疹、水痘等疾病,病人在治愈后具有了免疫力,不会再次被感染也不会传播疾病,可以用SIR模型来模拟。
3)SEIR模型:在SIR模型基础上,节点增加了一个暴露态E。易感节点S在接触I态节点后不是立即转换为I态,而是先经过一段时间的潜伏态E,再以一定概率变为I态或S态。在疫情传播中,感染节点如果自身具有较强的免疫能力,在患病后自行恢复,转变为健康个体。若感染节点自身抵抗力较弱,疾病不但不能被自身消除还会感染他人,这对应于E态节点转变为I态。含有潜伏期的传播模型还有SEIS、SEIRS模型等。
在经典传播模型的基础上,国内外学者研究了不同免疫策略下,传播模型的变化。Fu等[13]详细介绍了在部分免疫、目标策略、熟人免疫、活跃免疫等多种免疫策略下,SIS模型及其传播阈值的改变。Shi等[14]提出了不完全免疫的SIS模型,研究在无标度网络上传播阈值和免疫失效率的关系,发现在免疫控制下传播结果不仅与网络结构有关,还与免疫药物的有效期有关。Chen等[15]在SEIR模型中引入直接免疫率,处于潜伏态的节点以一定概率直接变为免疫个体。此外,引入外部舆论场影响率来研究传播模型的变化。Wang等[16]研究了有免疫失败和免疫失效时,病毒在SIR模型上传播行为的变化。Chen等[17]考虑舆情传播中话题具有衍生性、复杂性等特点,提出基于话题衍生性的SEIRS舆情传播演化模型,发现了网络舆情演化对传播规律的影响。
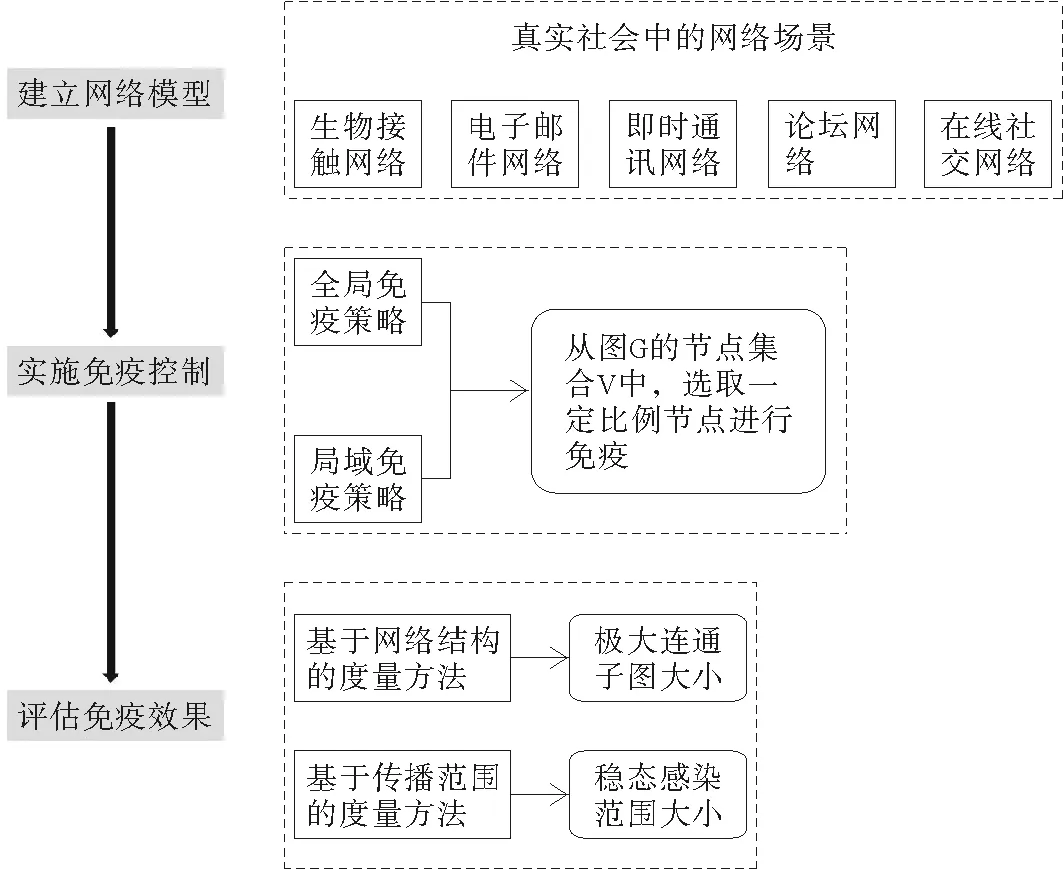
图1 基于复杂网络的免疫过程
3复杂网络上的免疫
基于病毒传播的机理,人们采用免疫的方法来控制传播。节点一旦被免疫,意味着从网络中删除了与这些节点相连的边,使得病毒传播的途径大大减少。免疫会产生经济方面的问题,比如注射疫苗有经济成本,也有对人体产生副作用的安全成本。当成本和资源有限时,选择最优的免疫策略,用最少的免疫量来最大限度地控制疫情和舆情的爆发,具有立刻可见的实用性和经济性[9]。基于复杂网络的免疫过程可以分为3个阶段:建立网络模型、实施免疫控制、评估免疫效果,如图1所示。
根据真实社会场景收集节点和连边信息,建立复杂网络模型,表示成图G=
3.1免疫效果的度量方法
在大多数免疫相关的研究中,对免疫效果的度量主要采用以下两种方法及其变形,即基于网络结构的度量方法和基于传播范围的度量方法。
基于网络结构的度量方法。基于网络结构的免疫效果度量,考察网络极大连通子图的大小如何随着免疫节点从网络中被移除而改变。免疫节点可以看作将节点和它的连边从网络中删除。节点一旦孤立,病毒就无法传播。只有处在极大连通子图中的感染节点,才能继续扩大感染范围。考虑一个无向无权网络,规模为N。被删除节点比例为p(0≤p≤1),剩余节点比例为1-p。网络在删除免疫节点之后,极大连通子图所包含的节点比例记为S。在一定的p下,S值越小,说明移除节点后剩余网络的极大连通子图规模越小,网络破碎程度越大,免疫策略效果越好。
基于传播范围的度量方法。该方法通过在传播模型上模拟病毒传播过程,考察传播进入稳定状态时网络中感染节点的比例。初始时,对目标节点进行免疫,且网络中仅有小比例的节点被感染。被免疫的节点在传播过程中既不会被感染,也不会传播疾病。疾病基于传播模型如SIS,SIR,SEIR进行传播。当传播达到稳态时,考察感染密度I*或R*随免疫密度p变化的函数。当施加相同的免疫剂量时,I*或R*的减小越多,免疫策略越有效。有时人们也会关注免疫临界gc,它代表使病毒无法传播时,即传播范围趋于0时,需要免疫的节点比例。免疫临界值越小,免疫策略效果越好。
3.2基于全局信息的免疫策略
免疫算法根据其依赖的网络信息完整程度可以分为两类:基于全局信息的免疫和基于局域信息的免疫。基于全局信息的免疫需要知道网络结构的完整信息,即每一个节点全部邻居的数量和对象。基于局域信息的免疫不需要网络完整的结构信息,只需要知道特定节点的局域信息,并以此决定免疫目标。利用网络完整的结构信息识别重要节点,比如求解特征向量中心性需要知道整个网络的邻接矩阵。一旦网络结构确定,依据不同策略选择的目标节点就固定下来,因此也称为确定性免疫策略。
3.2.1基于中心性的免疫
基于中心性的免疫策略的基本思想是,对节点的重要性进行排序,按照排序从高到低的顺序选择免疫目标。节点的重要性也称为“中心性”,中心性高的节点往往具有更大的传播影响力,如Twitter中少数重要节点的微博能很快传播网络;全球经济网络中核心国家的经济动荡会引发全球经济危机。Kang[18]利用中心性理论识别舆情传播中的关键节点,发现中心关键节点的资源控制能力与信息输入输出效率具有显著的正相关性。Cao等[8]发现在突发事件的舆情传播中,网络论坛中中心性高的节点能影响舆情演变,并发现“网络名人型”和“事件关注型”两类关键节点的演化规律。复杂网络理论中常用的中心性指标有度中心性、介数中心性、接近中心性、特征向量中心性和k-壳中心性。Lü等[19]指出,相比于随机免疫,基于中心性识别重要节点并免疫,能有效地影响网络传播的可控性。
1)度中心性。节点i的度是指与i直接相连的节点数目。度中心性认为一个节点的邻居数目越多,该节点的影响力越大。度中心性的计算复杂度为O(N),是最常用、最简单的中心性指标。经典的目标免疫算法就是利用度中心性选择免疫目标。在WS和BA模型网络上的免疫研究发现,无标度网络中免疫阈值的消失是由于度分布的异质性,基于节点度的目标免疫能大大降低网络对传播攻击的脆弱性[20]。
2)介数中心性。Freeman于1977 年提出介数中心性,它认为网络中连接所有节点对的最短路径中,经过某个节点的最短路径数目越多,这个节点就越重要。介数中心性刻画了节点对网络中沿最短路径传输的网络流的控制能力。节点i的介数定义为
(1)
3)接近中心性。接近中心性认为一个节点到网络中其它节点的平均距离越小,该节点位于网络越中心的位置[23]。对于有N个节点的连通网络,节点i的接近中心性被定义为i到其余节点的平均距离的倒数:
(2)
接近中心性对类似于星形网络的结构可以准确地发现中心节点,但对于随机规则网络却不适用。当信息或疾病从某节点向网络其余部分传播时,接近中心性高的传播源具有较短的平均传播距离,因而能更快速地传播信息与疾病。该算法的时间复杂度为O(N3)。
4)特征向量中心性。特征向量中心性的基本思想是:节点的重要性既取决于它邻居的数目,也取决于它邻居的重要性。如果一个节点的邻居很重要,这个节点的重要性很可能较高;如果邻居的重要性低,既使该节点有很多邻居,它也未必重要。节点i的特征向量中心性定义为
(3)
其中,ρ为常数,Гi为节点i的邻居集合,Aij为网络邻接矩阵。节点的特征向量中心性就是网络邻接矩阵最大特征值对应的特征向量。从传播的角度看,特征向量中心性适合于描述节点的长期影响力,如在疾病传播、谣言扩散中,特征向量中心性大的节点传播影响范围越大,是需要防范的关键[24]。特征向量中心性思想也被推广到有向网络用于识别重要节点,典型的算法有PageRank,HITs等。该算法的时间复杂度为O(N2)。
5)k-壳中心性。k-壳中心性通过k-壳分解算法将网络分层,为节点赋予核心性指标ks,以区分节点在网络中的位置重要性。ks值越大,表明节点位于网络越核心的位置,与网络其余部分的连接越紧密,传播影响力越大[25]。k-壳算法过程如下:首先从网络中删去度为1的节点及其连边。当全部度为1的节点被删除后,网络中可能会出现新的只有一条边的节点,继续删去这些节点,直到不存在度为1的节点为止。这些被删掉的节点被赋予核心性ks=1。按照类似的方法,剥掉网络中度为2的节点,它们具有核心性ks=2。继续删除更高的壳层,直到网络中每个节点被赋予一个ks值。在医院患者关系网络和演员合作网络上的研究表明,核心性高的节点是最有影响力的传播源[25]。在Twitter网络上,核心性高的节点发表的观点更容易被人追捧和扩散[26]。k-壳分解算法被推广到带权网络上[27],识别全球经济网络中最可能引发经济危机的国家。k-壳中心性具计算复杂度低的优点,为O(N)。
k-壳中心性虽然可以用于识别位于网络核心位置的节点,但是在实施免疫时,免疫的对象往往是网络中一定比例的节点而不是单个节点。当按照ks值从高到低的顺序来选取免疫目标时,同时免疫ks值高的节点反而降低了免疫效率。这是因为ks值高的节点常常相互连接,同时免疫它们使得许多边被重复隔离。Liu等[28]最近的研究发现,k-壳分解方法并非在所有真实网络中都能准确定位网络的动力学核心。在有的真实网络中,由于类核团的存在,k-壳分解方法找到的网络核心节点不是网络最有影响力的传播源。如何利用核心性进行有效免疫值得进一步研究。
Iyer等[29]在真实网络和模型网络上比较了基于不同中心性的免疫效果。在BA模型网络和ER模型网络中,度中心性对网络的破碎程度最大,然后依次是介数中心性、接近中心性和特征向量中心性。度中心性与介数中心性的表现非常接近,这是因为在这两种模型网络中两者的相似性很高。在没有特殊的结构特征时,考虑节点的度是最好的检测重要节点的方法。但是,当网络中有许多小度节点作为桥节点连接不同社区时,介数中心性就是更好的方法。在真实网络中,与在模型网络中结果类似,基于度和介数中心性的目标免疫是分割网络最有效的方法。同时,基于动态中心性的目标免疫方法比对应的基于静态中心性的方法破碎网络效果更好。基于不同中心性的目标免疫的效果明显比随机免疫好,这说明对真实数据的采集、建模和分析对传播控制具有实际意义[30]。
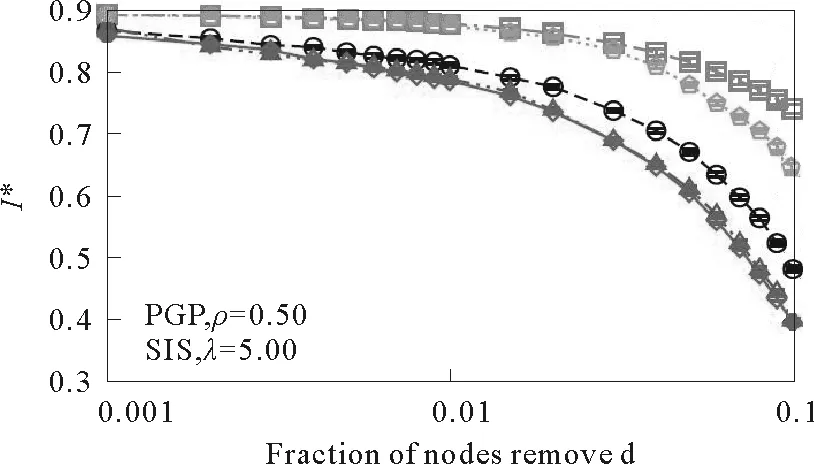
社区密度ρ=0.50,有效感染率λ=5.00。基于社区成员数目的免疫(菱形)效果好于或接近于基于介数中心性(三角)、度(圆圈)、k-壳中心性(五角)和随机节点(方形)的免疫。
除了上述常用中心性以外,Dufresne等[31]考虑以节点所属社区数目作为中心性指标来定位免疫目标,发现在特定的有效传播率时,该方法好于或者接近于介数中心性的免疫效果。图2展示了演员合作网上采用基于传播范围的度量方法时,中心性免疫的效果对比。
Lü[24]和Liu[32]等比较了各种中心性的优缺点及适用环境,指出节点重要性排序不仅与网络结构有关,还受网络传播机制及节点自身属性的影响。在选用中心性方法定位免疫目标时,还需要考虑节点本身的特征及传播机制。
3.2.2其它免疫策略
在目标免疫时,免疫节点由于断开了与其邻居节点的连边,将网络分割成若干个集团。但是这些集团的大小分布很广,有大量规模非常小的集团。免疫策略实际上浪费了许多剂量在分割那些极小规模的集团上。Chen等[33]提出了一种“相等图划分”(Equal Graph Partition, EGP)的免疫策略。EGP的主要思想是,将网络划分成相互连接的、几乎相同大小的子图(社团)。与目标免疫相比,该算法能够减少约5%~50%的免疫剂量。在随机网络、无标度网络、随机规则网络和真实网络上的模拟结果表明,EGP免疫策略通过分割网络来限制疾病传播,比目标免疫策略所需要的免疫剂量更少。图3展示了在4个真实网络中,几个免疫策略的对比。在所有的网络中,EGP算法都表现更好。
Huang等[34]对复杂网络的节点进行着色,提出了基于着色的免疫策略。根据着色原理,任意两个相邻的顶点被着以不同的颜色。着色完成后,相同颜色的节点形成独立集,独立集内任意两个节点不直接相连。通过从含有节点数目最多的独立集中随机选择节点进行免疫与从整个网络随机选择节点进行免疫相比较,发现基于独立集的随机免疫效果明显好于经典的随机免疫。这是因为独立集节点互不相连,免疫这些节点对网络连通性的破坏更大。基于独立集的免疫策略提供了研究免疫的新思路,即免疫距离较远的节点集合能取得更好的免疫效果。进一步地,Zhao等[35]研究如何寻找网络上最有效的多点传播源,发现相比于在整个网络中选取中心性排序在前的节点,在独立集中选择中心性高的节点作为多点传播源能最大化传播的广度和加速传播的过程。这一结论启示我们可以通过在独立集中选择中心性高的节点进行免疫。
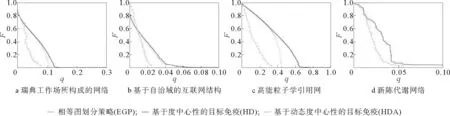
图3 可被感染的最大连通簇的比例F与免疫比例q的关系[33]
当疫情和舆情爆发时,个体会根据自身状况对疾病和信息的传播作出反应。如处在流行病爆发区的人群会倾向于接种疫苗,政府会采取预警和应对措施。Zhang等[36]基于博弈思想,研究了自我接种机制对疾病传播的影响。由于是否采取免疫行为都有一定的成本,个体会平衡接种和不接种的代价。当接种代价小于被感染的代价时,个体就采取接种行为。研究发现,自愿接种机制下,在无标度网络上能够比在随机网络上更有效地控制疾病的传播。这是由于度大节点被感染的风险更大,因此它们更倾向于采取免疫行为,从而有效控制了疾病的传播。进一步地,Zhang等[37-38]研究了政府对免疫行为采取补贴政策时,免疫率的提升。在基于博弈演化理论的自愿接种模型中,个体将最大化其免疫收益。但仅仅是自愿接种并不足以有效控制疾病传播,政府提供的补贴政策会对免疫覆盖产生重要作用。研究发现,对个体免疫成本的部分补贴策略能鼓励更多的人采取免疫行为,而对一部分个体进行完全补贴时,对大度节点补贴比对随机节点补贴能更明显地提升免疫效果。此外,在部分补贴策略下,免疫的覆盖范围单调依赖于个体对免疫代价的敏感度,而在完全免疫策略下,该依赖性并不单调。Ruan等[39]研究了个体危机意识对免疫策略的影响,提出了信息驱动免疫。通过引入信息产生率和信息敏感率来量化信息驱动的免疫。信息敏感率越高,采取免疫行为的概率越大。模拟结果发现当信息产生率和信息敏感率较大时,疾病的传播明显减小,需要的免疫计量也大大减少。
免疫节点的方法虽然有效,但却破坏了网络的连通性,比如在Internet中关闭度大的路由器会影响网络的可达性。Zhang等[40]提出基于删边的免疫策略,通过删去连接大度节点的边可以有效控制疾病的传播。Wang等[41]研究了网络度分布和权重分布对传播阈值和传播范围的影响,发现增加权重分布的异质性能降低疾病传播的范围。在感染概率较低时,增加度分布的异质性能增加传播范围;在感染概率较大时,增加度分布的异质性却能降低传播范围。进而提出一种基于边权的删边策略,通过优先删除边权较大的边,能有效地控制传播,尤其是在权重分布具有较强的异质性和度分布具有同质性的网络上。
3.3基于局域信息的免疫策略
全局策略能够较为准确地识别关键节点,免疫效果明显。然而对于大规模网络,我们很难及时获知网络的全部信息,对网络结构的运算复杂度也往往较高,无法确保及时识别出关键节点。局域免疫策略是在对网络全局信息未知的情况下,利用节点周围的局部信息,选取目标控制节点。局域免疫策略只需要少量的局域信息就能快速有效地识别免疫目标,从而控制疾病在整个网络中的传播,因而更具有实际的可操作性。局域免疫策略也称为不确定性免疫策略。
3.3.1随机免疫
随机免疫[42]是完全随机地选取网络中的一部分节点进行免疫,是最简单的免疫方法。随机免疫需要免疫大量人群来阻止接触过程中的疾病传播,许多疾病需要免疫80%~100%的节点,如风疹需要免疫95%的人群。对因特网来说,阻止计算机病毒需要几乎100%的免疫。随机免疫通常用作检验其它免疫方法效果的基准。
3.3.2熟人免疫
由于随机免疫需要免疫大比例的节点,实施免疫时代价较高,Cohen等[43]提出了熟人免疫算法。它的算法流程是:随机选择一个节点v0,然后随机选择它的n个熟人,也就是v0的n个随机选择的邻居,将选出的熟人进行免疫。下一步继续随机选择被免疫的节点的邻居,直到达到设定的免疫比例。熟人免疫策略可以识别高度连接的个体,特别是在无标度网络中。这是因为大度节点有大量的连接,一个随机节点的邻居是大度节点的概率很大,因此大度节点更容易被选中。
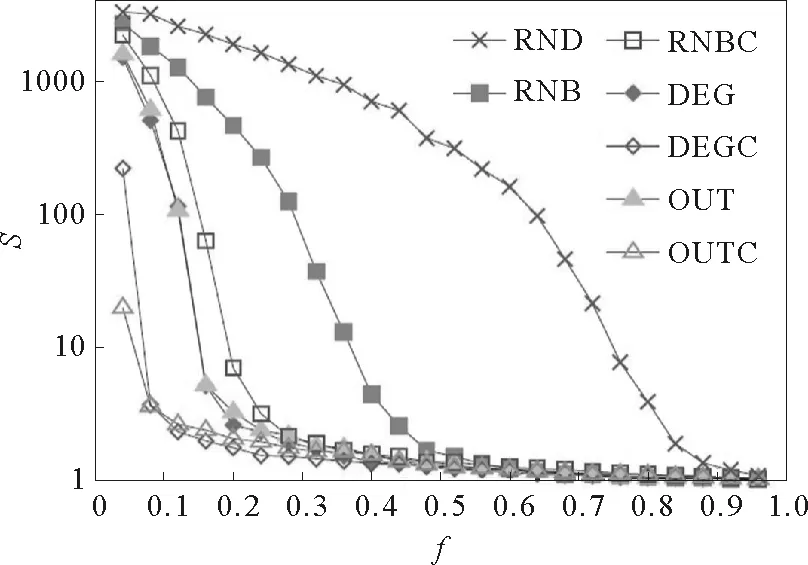
图4 感染节点数目S随免疫比例f的变化[45]
熟人免疫的一种改进策略是:若随机节点的熟人的度比该节点的度大,则免疫该节点。如果不存在这样的邻居,就重新选择一个随机节点。该方法的一个变形是,找到随机节点的熟人,其连接数目应大于指定的值k,比如k=5。该策略仅基于局域信息,却能使免疫效果接近于目标免疫[44]。另一个类似的改进策略由Holme[45]提出:选择随机节点度最大的邻居进行免疫。为了避免过分免疫同一个邻居集,考虑免疫具有最大连出边数的邻居(指连出该随机节点的邻居集)。在多个真实网络和模型网络上的模拟结果表明,Holme的改进策略在大多数情况下比熟人免疫效果更好。图4展示了arXiv合作网络上,基于SIR传播的几种免疫策略效果的对比。随机免疫(RND),熟人免疫(RNB),免疫随机节点度最大的邻居(DEG),免疫随机节点具有最大连出边数的邻居(OUT)。带C的曲线指的是连锁免疫,即免疫在前一时间步被免疫节点的邻居,而不带C的曲线在每一步都随机选择节点,然后选择该随机节点的邻居实施免疫。可以看出,改进的熟人免疫效果好于经典的熟人免疫,随机免疫效果最差。
3.3.3具有社区结构的网络上的局域免疫
在具有社区结构的网络中,连接不同社区的桥节点及弱连边在病毒的扩散过程中起着非常关键的作用,免疫桥节点能更加有效地控制传染病爆发。Salathé等[46]研究了社区结构对传播动力学的影响,提出了一种仅基于网络局域信息的社区桥节点发现策略(Community-Bridge-Finder,CBF),对发现的桥节点进行免疫。CBF算法采用随机游走识别桥节点,无需知道网络的全局结构,因此也不知道网络的社区结构。它的实现依赖于这一假设:当前随机游走下,第一个与之前访问的节点不相连的节点,很有可能属于另外一个社区。基于CBF的免疫在具有较强社区效应的网络上免疫表现非常好。Gong等[47]对实际网络的社区结构进行深入分析,发现桥节点的弱连接数存在一定的异质性,即桥节点中存在少数更加重要的桥中心节点,它们比其它桥节点具有更多的弱连边。基于自避免随机游走和对比已有朋友圈与当前节点邻域的重叠度,提出桥中心点发现算法(Bridge-Hub Detector,BHD)。在模型社区网络和真实社区网络上的模拟结果表明针对桥节点及桥中心节点的免疫比熟人免疫和CBF算法的免疫效果都好。Yang等[48]研究了自适应网络上的传播过程,发现在疾病传播早期,由于断边重连机制的存在,易感节点S与感染节点I发生断边行为,形成较强的社区结构。利用节点局域信息,如节点及其邻居当前的状态和数目,识别S社区与I社区之间的桥节点并实施免疫,能有效延缓传播速度,减小传播范围。此外疾病的控制并非越早越好,而应当在社区效应较强时进行控制。Wang等[49]研究了通讯-接触耦合网络上,疾病和消息传播的相互影响对最终传播范围的影响。用SIR模型模拟消息传播,SIRV模型模拟疾病传播,建立通讯-接触耦合网络上的传播模型。基于平均场方法的解析与数值模拟结果表明通讯网络的异质性越强,免疫概率越大,疾病越不容易爆发。
4小结与思考
如何有效地控制疫情和舆情是网络科学的重要课题之一。网络免疫是复杂网络传播动力学研究的一个重要内容,是抑制疫情和舆情传播的重要方法。本文对基于复杂网络的免疫控制方法进行了系统的评述,包括实际网络传播的抽象、疫情和舆情的传播模型、免疫效果的度量、全局免疫策略以及局域免疫策略等。这有助于关注这个课题的不同学科的人们认识和理解已有免疫策略的研究现状,在此基础上进一步开拓创新。为此,这里提出若干值得思考和研究的问题。
第一,由于实际网络结构的复杂性和时序性,以及人类行为的异质性,基于不同的网络结构特征和传播行为的网络免疫算法有待进一步研究,亟需来自不同领域的研究学者驱动创新。比如,流行病传播模型与真实世界的传播行为有一定差异。人类社会具有社区性,人的活动具有一定目的性,传播过程并不等同于复杂网络上的随机游走。个体差异使得网络中不同节点的感染概率和恢复概率并不总是相同,而节点的传播能力也并非与其连接数目成线性关系等[50]。
第二,各种疫情和舆情的实际传播机制既有共性,也存在着差异性,因此具体问题要具体分析,不能以一概全。例如,埃博拉病毒通过朋友、家庭、医生护士等进行传播,比以往的病毒传播方式更为复杂。因此,需要了解疫情传播时真实的接触行为和途径。人们是否获知疫情发生以及在获知疫情后的行为反应,受到周围信息和个体意识的重要影响。我们面对多层次流行病传播时,需要新的分析研究方法。
第三,舆情通过互联网传播,在舆情发生时,更容易引起人们的关注从而增加人的参与度。疫情的传播有可能引起舆情,舆情的传播反过来会对疫情产生抑制或者促进作用。疫情和舆情的传播由于时间上的交替出现还具有随时间和空间变化的特性。研究耦合网络和时序网络上的传播对免疫策略的制定具有实际意义。
第四,理论研究的成果需要实际数据的验证和支持。在大数据时代,基于大数据的疫情和舆情的传播研究更要重视大数据的挖掘和分析,以便发现新问题,确定新策略。在实践中,政府部门建立的突发事件信息监测系统应当为分析和评估事件提供可靠的大数据支持,进而在对数据结构化的基础上,建立合适的传播模型,分析传播载体结构特征,以便采用适当的免疫策略,对舆情与疫情进行有效的管理控制。本文提供的一些方法和思考不仅希望为相关决策部门的应急管理提供建设性意见和参考,而且也为继续深入研究疫情与舆情的管控打下理论基础,以便为预警与控制以网络为载体的疫情与舆情传播提供有效的管控方法和切实措施。
参考文献:
[1]周涛, 汪秉宏, 韩筱璞, 等. 社会网络分析及其在舆情和疫情防控中的应用[J]. 系统工程学报. 2010, 25(6):742-754.
Zhou Tao, Wang Binghong, Han Xiaopu, et al. Social network analysis and its application in the prevention and control of propagation for public opinion and the epidemic[J]. Journal of System Engineering, 2010, 25(6):742-754.
[2]庄亚明, 余海林. 群体性突发事件信息传播网络特性研究——以抢蜡烛事件为例[J]. 情报杂志,2013, 32(7):37-42.
Zhuang Yaming, Yu Hailin. Research on characteristics of information propagation network of the mass unexpected incident: a case analysis of panic buying of candles[J]. Journal of Intelligence, 2013, 32(7):37-42.
[3]汪小帆, 李翔, 陈关荣. 网络科学导论[M]. 北京:高等教育出版社,2012.
[4]周涛,傅忠谦,牛永伟,等. 复杂网络上传播动力学研究综述[J]. 自然科学进展,2005,15(5): 513-517.
Zhou Tao, Fu Zhongqian, Niu Yongwei, et al. Review on spreading dynamics on complex network[J]. Advance in Natural Science, 2005, 15(5): 513-517.
[5]马知恩, 周义仓, 王稳地,等. 传染病动力学的数学建模与研究[M]. 北京:科学出版社,2004.
[6]Newman M E J, Forrest S, Balthrop J. Email networks and the spread of computer viruses[J]. Physical Review E, 2002, 66(3):035101(R) (1-4).
[7]高超,刘际明,钟宁,等. 邮件网络中基于介数的免疫策略研究[J]. 计算机工程. 2010, 36(5), 18-20.
Gao Chao, Liu Jiming, Zhong Ning, et al. Research on betweenness-based immunization strategy in email networks[J]. Computer Engineering, 2010, 36(5), 18-20.
[8]曹学艳, 段飞飞, 方宽, 等. 网络论坛视角下突发事件舆情的关键节点识别及分类方法[J]. 图书情报工作,2014, 58(4):65-70.
Cao Xueyan, Duan Feifei, Fang Kuan, et al. Research of identification and classification of emergencies key nodes based on BBS[J]. Library and Information Service, 2014, 58(4):65-70.
[9]杨洪勇, 张嗣瀛. 基于复杂网络的禽流感病毒传播[J]. 系统仿真学报, 2008, 20(18):5001-5005.
Yang Hongyong, Zhang Siying. Viruses epidemics of avian influenza based on complex networks[J]. Journal of System Simulation, 2008, 20(18):5001-5005.
[10] Carmi S, Havlin S, Kirkpatrick S, et al. A model of internet topology using k-shell decomposition[J]. Proc Nat Acad Sci, 2007, 104(27): 11150-11154.
[11] Pastor-Satorras R, Vespignani A. Epidemic dynamics and endemic states in complex networks[J]. Phys Rev E, 2001, 63(6): 066117.
[12] Anderson R M, May R M. Infectious Diseases of Humans[M]. Oxford: Oxford University Press, 1991.
[13] Fu X C, Small M, Chen G R. Propagation Dynamics on Complex Networks-Models, Methods and Stability Analysis[M]. Beijing: Higher Educational Publishing, 2014:251-258.
[14] Shi H J, Duan Z S, Chen G R, et al. Epidemic spreading on networks with vaccination[J]. Chinese Phys B, 2009, 18(8), 3309-3317.
[15] 陈波,于泠,刘君亭,等. 泛在媒体环境下的网络舆情传播控制模型[J]. 系统工程理论与实践,2011, 31(11): 2140-2150.
Chen Bo, Yu Ling, Liu Junting, et al. Dissemination and control model of internet public opinion in the ubiquitous media environments[J]. Systems Engineering-Theory&Practice, 2011, 31(11): 2140-2150.
[16] 王亚奇,蒋国平. 复杂网络中考虑不完全免疫的病毒传播研究[J]. 物理学报,2010, 59(10): 6734-6743.
Wang Yaqi, Jiang Guoping. Virus spreading on complex networks with imperfect immunization[J]. Acta Phys Sin, 2010, 59(10): 6734-6743.
[17] 陈福集, 陈婷, 郑小雪. 一类新SERIS模型上的网络舆情传播行为研究[J]. 情报资料工作, 2014, 4: 62-67.
Chen Fuji, Chen Ting, Zheng Xiaoxue. An analysis of Internet public opinion propagation behavior based on a new SEIR Model[J]. Info and Doc Services, 2014, 4: 62-67.
[18]康伟. 基于SNA的突发事件网络舆情关键节点识别[J]. 公共管理学报, 2012, 9(3):101-111.
Kang W. Analysis of the key nodes in public opinion spread during emergencies based on social network theory[J]. Journal of Public Management. 2012, 9(3):101-111.
[19] 吕天阳,朴秀峰,谢文艳, 等. 基于传播免疫的复杂网络可控性研究[J]. 物理学报, 2012, 61(17):170512.
Lü Tianyang, Piao Xiufeng, Xie Wenyan, et al. Controllability of complex networks based on epidemic vaccination[J]. Acta Phys Sin, 2012, 61(17) :170512.
[20] Pastor-Satorras R, Vespignani A. Immunization of complex network[J]. Phys Rev E, 2002, 65(3): 036104.
[21] Holme P, Kim B J. Attack vulnerability of complex networks[J]. Phys Rev E, 2002, 65(5): 056109.
[22] Schneider C M, Mihaljev T, Havlin S, et al. Suppressing epidemics with a limited amount of immunization units[J]. Phys Rev E, 2011, 84(6): 061911.
[23] Sabidussi G. The centrality index of a graph[J]. Psychometrika, 1966, 31: 581-603.
[24] 任晓龙,吕琳媛. 网络重要节点排序方法综述[J]. 科学通报,2014,59(13): 1175-1197.
Ren Xiaolong, Lü Linyuan. Review of ranking nodes in complex networks[J]. China Science Bulletin, 2014, 59(13):1175-1197.
[25] Kitsak M, Gallos L K, Havlin S, et al. Identification of influential spreaders in complex network[J]. Nature Phys, 2010, 6: 888-893.
[26] Brown P E, Feng J L. Measuring user influence on twitter using modified k-shell decomposition[C]//Fifth International AAAI Conference on Weblogs and Social Media. Barcelona: AAAI, 2011:18-23.
[27] Garas A, Schweitzer F, Havlin S. A k-shell decomposition method for weighted networks[J]. New J Phys, 2012, 14: 083030.
[28] Liu Y, Tang M, Zhou T, et al. Core-like groups result in invalidation of identifying super-spreader by k-shell decomposition[J]. Sci Rep, 2015, 5:9602.
[29] Iyer S, Killingback T, Sundaram B, et al. Attack robustness and centrality of complex networks[J]. PLoS ONE, 2013, 8(4):e59613.
[30] Salathé M, Kazandjieva M, Lee J W, et al. A high-resolution human contact network for infectious disease transmission[J]. Proceedings of the National Academy of Sciences, 2010, 107(51):22020-22025.
[31] Hébert-Dufresne L, Allard A, Yong Y J, et al. Global efficiency of local immunization on complex networks[J]. Sci Rep, 2013, 3:2171.
[32] 刘建国,任卓明,郭强,等. 复杂网络中节点重要性排序的研究进展[J]. 物理学报,2013, 62(17):178901.
Liu Jianguo, Ren Zhuoming, Guo Qiang, et al. Node importance ranking of complex networks[J]. Acta Phys Sin, 2013, 62(17): 178901.
[33] Chen Y P, Paul G, Havlin S, et al. Finding a better immunization strategy[J]. Phys Rev Lett, 2008, 101(5): 058701.
[34] 黄斌,赵翔宇, 齐凯,等. 复杂网络的顶点着色及其在疾病免疫中的应用[J].物理学报, 2013, 62(21):218902.
Huang B, Zhao X Y, Qi K, et al. Coloring the complex networks and its application for immunization strategy[J]. Acta Phys Sin, 2013, 62(21):218902.
[35] Zhao X Y, Huang B, Tang M, et al. Identifying effective multiple spreaders by coloring complex networks[J]. Euro Phys Lett, 2014, 108: 68005.
[36] Zhang H F,Zhang J,Zhou C S,et al. Hub nodes inhibit the outbreak of epidemic under voluntary vaccination[J].New J Phys,2010,12: 023015.
[37] Zhang H F, Wu Z X, Xu X K, et al. The impacts of subsidy policies on vaccination decisions in contact networks[J]. Phys Rev E, 2013, 88:012813.
[38] Zhang H F, Wu Z X, Tang M, et al. Effects of behavioral response and vaccination policy on epidemic spreading-an approach based on evolutionary-game dynamics[J]. Sci Rep, 2013, 4:5666.
[39] Ruan Z Y, Tang M, Liu Z H. Epidemic spreading with information-driven vaccination[J]. Phys Rev E, 2012, 86:036117.
[40] Zhang H F, Li K Z, Fu X C, et al. An efficient control strategy of epidemic spreading on scale-free networks [J]. Chin Phys Lett, 2009, 26:068901.
[41] Wang W, Tang M, Zhang H F, et al. Epidemic spreading on complex networks with general degree and weight distributions[J]. Phys Rev E, 2014, 90: 042803.
[42] Pastor-Satorras R, Vespignani A. Immunization of complex networks[J]. Phys Rev E, 2002, 65:036104.
[43] Cohen R, Havlin S, ben-Avraham D. Efficient immunization strategies for computer networks and populations[J]. Phys Rev Lett, 2003, 91(24):247901.
[44] Gallos L K, Liljeros F, Argyrakis P, et al. Improving immunization strategies[J]. Phys Rev E, 2007, 75(R): 045101.
[45] Holme P. Efficient local strategies for vaccination and networks attack[J]. Euro Phys Lett, 2004, 68(6):908-914.
[46] Salathé M, Jones J H. Dynamics and control of diseases in networks with community structure[J]. PLoS Comp Bio, 2010, 6(4):e1000736.
[47] Gong K, Tang M, Hui P M, et al. An efficient immunization strategy for community networks[J]. PLoS ONE, 2013, 8(12):e83489.
[48] Yang H, Tang M, Zhang H F. Efficient community-based control strategies in adaptive networks [J]. New J Phys, 2012(14): 123017.
[49] Wang W, Tang M, Yang H, et al. Asymmetrically interacting spreading dynamics on complex layered networks[J]. Sci Rep, 2014, 4:5097.
[50] 李翔,刘宗华,汪秉宏. 网络传播动力学[J]. 复杂系统与复杂性科学,2010, 7(2/3): 33-37. Li Xiang, Liu Zonghua, Wang Binghong. On spreading dynamics on networks[J]. Complex System and Complexity Sciense, 2010, 7(2/3): 33-37.
(责任编辑李进)
Controlling Epidemic Outbreaks and Public Sentiment Spreading by Vaccination in Complex Network
LIU Ying1,2, WANG Wei1, SHANG Mingsheng1, TANG Ming1
(1. Web Sciences Center, University of Electronic Science and Technology of China, Chengdu 611731, China;2. School of Computer Science, Southwest Petroleum University, Chengdu 610500, China)
Abstract:In this paper, an overview of vaccination methods addressing in suppressing the epidemic spreading is given, focusing on modeling the epidemic and public sentiment spreading from real world scenarios, describing models of dynamic spreading, and presenting vaccination strategies and their efficiency. Simulation results on empirical networks and model networks using different vaccination strategies show that vaccination strategies such as centrality-based vaccination, graph partition-based vaccination and acquaintance vaccination are more effective than random vaccination. This implies that vaccination strategy is important and meaningful in suppressing epidemic spreading. In order to reach a better control result, the topological structure and the completeness of network information should be taken into account when choosing a vaccination strategy.
Key words:complex network; spreading dynamics; epidemic and public sentiment spreading; network vaccination
文章编号:16723813(2016)01007410;
DOI:10.13306/j.1672-3813.2016.01.007
收稿日期:2015-05-07
基金项目:国家自然科学基金(11105025,91324002);西南石油大学科研启航计划(2014QHZ024)
作者简介:刘影(1980-),女,山东烟台人,博士研究生,主要研究方向为复杂网络传播动力学。
通讯作者:唐明(1981-),四川资阳人, 博士,副教授,主要研究方向为复杂网络传播动力学。
中图分类号:C93; N93
文献标识码:A
