ANSYS CFX在哈根-泊肃叶方程教学实践中的应用
2016-06-20李光明郑丽璇
李光明,徐 斌,郑丽璇
(西南科技大学,四川 绵阳 621010)
ANSYS CFX在哈根-泊肃叶方程教学实践中的应用
李光明,徐斌,郑丽璇
(西南科技大学,四川 绵阳621010)
摘 要:在对哈根-泊肃叶方程理论分析和推导的基础上,借助于ANSYS CFX进行流场的数值计算,获得速度场和剪切速率的分布以及壁面的剪切应力等多个物理量的分布以及较为直观的可视结果和可靠数据,进一步的提高了教学效果,促进了学生的理解能力与动手实践的兴趣。
关键词:哈根-泊肃叶方程;ANSYS CFX;牛顿流体;数值模拟
流变学作为材料成型等专业的主要理论基础课程,通过对材料流动和变形现象的描述,可以有效的理解和把握特定结构下聚合物熔体的流变行为,如速度、压力、温度等分布规律,能够更进一步地指导塑料成型加工和模具设计。其中,著名的哈根-泊肃叶方程在流变学领域首次从理论上证实了牛顿黏性假设、壁面不滑移假设的正确性,是毛细管黏度计的设计原理,同时也是非牛顿熔体流动许多关键规律的推导基础。因此,其理论学习和实践验证在相关专业的教学中占有相当重要的地位。
流变学课程的学习一般采用的手段主要为理论分析和实践认识。理论分析是应用基本物理定律建立方程,通过数学推导发现各种流动状态下相关参数之间的依赖关系。而实践认识往往需要配备各种测量和观察手段,如具有稳定的实验环境和较为齐全、精密的专业仪器设备对流动现象进行观测,对流动规律进行验证。仅依赖设备会增加教学成本,同时也很难测定和描述某些物理参数。
随着信息和图形学技术的迅猛发展[1],为数值模拟工程分析等方面带来了革命性的变化,在国内高校教学及实验研究方面起到了日益重要的支撑作用。数值模拟技术在教学过程中提供了较为先进的实践分析和观测验证方式,能更直接的反映材料流变过程的物理现象,能在缺乏相关实验设备的条件下获得较为精准的实验数据和图表。ANSYS CFX作为世界上唯一采用全隐式耦合算法的大型商业软件,其算法上先进,具有丰富的物理模型和前后处理的完善性,在结果精确性、计算稳定性、计算速度和灵活性上都有优异的表现,能够模拟诸如燃烧,多相流,化学反应等许多现实复杂流场[2]。将ANSYS CFX灵活运用到流变学的教学实践中,一方面对于教学和实验的过程验证具有非常重要的意义,另一方面能提高学生的感性认识,激发他们的学习兴趣和积极性,能够深入理解流变过程的基本原理,培养设计和创新的能力。
1哈根-泊肃叶方程的理论分析及实验验证
不可压缩牛顿流体在圆管中的稳定流动也被称为泊肃叶(Poissuille flow)流动[3]。通过细圆管中流体流动的流量来测定黏度,常采用柱坐标(r,θ,z)进行描述,如图1所示。
牛顿流体在圆管两侧压力差△p的作用下,仅沿z轴方向流动,将圆管中的层流视为许多同轴圆柱层的流动,任一层流体引起的黏性阻力与外力构成了平衡,如下式(1)所示:
2πrlτrz+△pπr2=0
(1)
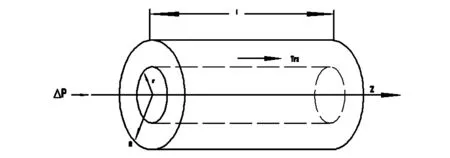
图1 物理结构模型
对牛顿流体在圆管中层流展开,根据理想线性黏性流变方程[4],建立关系式以获得速度分布方程,如下式(2)所示:
(2)
通过从r到r+dr的圆环柱体的单位体积流量积分得到整个圆管截面的流量,从而建立流量和黏度μ的内在关系,如下式(3)所示:
(3)
因此,在已知流体黏度和压力差的前提条件下,实验验证思路为通过ANSYS CFX环境理想化建模来描述真实流体的流动状态,实现数值计算,再对所得结果进行图形后处理分析,获得图形效果。借以对圆管内速度分布场、壁面的剪切应力和剪切速率进行仿真验证,进一步增强学生对圆管结构内牛顿流体平稳层流机理的理解。
2实验准备与数值模拟
2.1实验材料
本实验选用水作为研究对象,流体域设置在绝热环境内。在25 ℃的温度下,水的黏度为0.894 9×10-3pa·s-1,密度为997.05 kg/m3。
2.2数值模拟准备
构建细长圆管结构模型,其中长度为100 mm,直径为10 mm(满足r/l≪1),如图2所示。在ANSYS Workbench 环境中划分网格结构,采用边界层形式和四面体结构单元[5],网格结果如图3所示。

图2 圆管几何结构

图3 划分网格
3结果验证
在细长圆管两端设置压力差为20 pa,管内温度为25 ℃,设置为绝热状态,管壁设置为不可滑移面。采用Laminar流动模型,迭代次数为1 000次,残差目标为0.000 1,进行数值计算。
3.1圆管内的径向速度分布
水介质在圆管流道中流动时,根据推导公式进行径向速度分布的理论计算得到流道中心流速为0.013 97 m/s。图4为数值模拟的速度场分布,能够直观的看出圆管中心部位流速较高,流道壁附近的流速较低,且成二次曲线函数形式。

图4 管内流速分布
此外,图5为流线分布形式,能够很形象的描述水介质在圆管中的流动形态,如下图5所示。

图5 管内流线形态
3.2管壁剪切应力和管内剪切速率分布
对于管壁剪切应力和管内剪切速率,采用公式推导进行计算, 其中,剪切应力如下式(4) 所示,剪切速率参见公式(2)。
(4)
可以计算得到管壁处的最大剪切应力为0.05pa,剪切速率为55 s-1。对于理论值来说,数值计算结果非常接近,其分布状况如下图6和7所示,呈线性函数形式,在管壁处剪切应力和速率大,圆管中心小。

图6 管壁处剪切应力
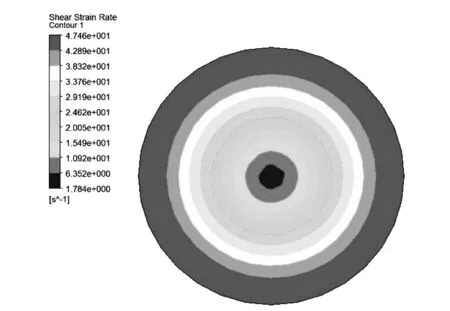
图7 管内剪切速率分布
通过上述数值模拟结果的分析和验证,可以让学生更形象、清晰地观察到水介质在圆管内稳定层流时,速度场和剪切速率的分布以及壁面的剪切应力等多个物理量的变化,对哈根-泊肃叶方程的原理、推导过程有更深入的理解。
4结论
本文借助于ANSYS CFX对牛顿流体的圆管内流动进行数值模拟,通过对哈根-泊肃叶方程原理的推导、数值模拟、图形结果的分析验证的有机结合,获得较为直观的可视效果和可靠的分析数据,能有效的改进和提升教学质量,使学生对牛顿流体的流动机理等知识有更深入的理解,并进一步培养和提高学生的理解能力和动手实践的兴趣。
参考文献:
[1]林琦.计算机信息网络技术在大学物理实验教学中的应用探讨[J].大学物理实验,2013,26(2).
[2]高飞,李昕.ANSYS CFX 14.0超级学习手册[M].北京:人民邮电出版社,2013.
[3]徐佩弦.高聚物流变学及其应用[M].北京:化学工业出版社,2003.
[4]赵汉中.工程流体力学[M].武汉:华中科技大学出版社,2005.
[5]容琼,吴静萍,姜曼松.圆管内流动的数值模拟[J].中国水运(理论版),2006,12.
The Application of ANSYS CFX in the Hagen-Poiseuille Equation in Teaching Practice
LI Guang-ming,XU Bin,ZHENG Li-xuan
(Southwest University of Science and Technology,Sichuan Mianyang 621010)
Abstract:The distribution of velocity and shear rate distribution and the wall shear stress and multiple physical quantities and more intuitive visual results and rely on the data are obtained on the basis of the Hagen-Poiseuille equation theoretical analysis and derivation,with in ANSYS CFX for flow field numerical calculation,and it further improves the teaching effect,promotes the students' understanding and practical interest.
Key words:Hagen-Poiseuille equation;ANSYS CFX;Newtonian fluid;numerical simulation
收稿日期:2015-10-28
基金项目:西南科技大学博士基金(11zx7108);西南科技大学实验技术研究项目(13syjs-47)
文章编号:1007-2934(2016)02-0038-03
中图分类号:O 4-39
文献标志码:A
DOI:10.14139/j.cnki.cn22-1228.2016.002.010
