基于粒子群优化算法的多元线性拟合方法研究及其应用

韩家兴，吴施楷，田仁飞*，李　杰，杨　宽

(成都理工大学　a.地球物理学院，b.沉积地质研究所，成都　610059)



基于粒子群优化算法的多元线性拟合方法研究及其应用

韩家兴a，吴施楷a，田仁飞a*，李杰b，杨宽a

(成都理工大学a.地球物理学院，b.沉积地质研究所，成都610059)

摘要：实际测井中，密度曲线最易受扩径的影响。为了消除这种影响，在多元线性拟合方法中引入了粒子群优化算法(Particle Swarm Optimization，PSO)，提出了基于粒子群优化算法的多元线性拟合方法，粒子群优化算法是对目标函数优化具有自适应控制的智能进化算法。这里将粒子群优化算法与多元线性拟合法结合，选取井眼环境好，且与扩径层段有相同的岩性、物性的井段作为参考层，利用受井眼环境影响相对小的测井曲线(伽马、电阻率和声波时差)，建立更加精确的多元线性拟合模型；再运用这个模型在扩径层段重构密度曲线；最后将重构密度曲线与原始密度曲线、Gardner公式计算的密度曲线进行对比分析。研究结果表明，提出的基于粒子群优化算法的多元线性拟合法重构的密度曲线的合成地震记录与井旁地震道相关系数可达0.86，说明该方法能够更有效提高密度测井曲线的质量。

关键词：粒子群算法；多元线性拟合；井间扩径；校正密度

0引言

测井是地球物理学的一个分支，它能够在井中连续测量地层的多种物理参数以及钻孔的几何参数等。密度曲线属于常规测井曲线，它的质量好坏直接会影响到我们对地下储层的评价与预测[1]。无论我们是做地震反演，还是做地震正演，都存在着一个基本假设：测井数据属于“硬数据”，真实可靠，可以反映地下地层的物理性质。但在现实当中，我们拿到的测井数据(特别是密度曲线[2-3])往往并没有我们想象的那么“硬”，因为测井仪器在井中测量的过程中会受到井眼环境的影响，或如井径不规则及井壁塌陷等，也会对测井质量造成严重影响[4-5]。所以，我们在做地震反演之前，必须要对密度曲线的基础资料作质量评价，必须消除曲线失真的影响，因此，有必要对测井曲线进行校正。

目前测井曲线校正方法比较多。黄超等[5]归纳的测井校正方法有：经验公式法、岩石物理建模法和多元线性拟合法。其中，多元线性拟合法在扩径对密度曲线影响中效果较好，但多元线性拟合模型的建立是关键。粒子群优化算法是由Kennedy和Eberhart[6-7]提出的一种基于智能的进化算法。在目标函数优化、自适应控制、组合优化、人工生命、管理决策等领域得到了广泛地应用[8]。这里在分析川西某地区CK井密度和井径曲线中，发现目标层段的部分测井曲线受井径影响较大。在此基础上，提出适合该地区的基于粒子群优化算法的多元线性拟合公式，并与Gardner经验公式[9]和原始密度曲线对比分析，结合井震标定的相关性，验证了作者提出的基于粒子群优化算法的多元线性拟合公式的合理性和有效性。

1粒子群优化算法

粒子群优化算法，又称为微粒群优化算法，是智能算法的一种，源于对鸟群觅食过程中的迁徙和聚集的模拟[7]。首先，POS随机生成一群粒子，每一个粒子都是优化函数的可行解，目标函数为每个粒子确定适应值，粒子在解空间运动方向和距离由一个速度决定。通常粒子会追随目前所找到的最优解，随着叠代次数的增加，最终找到解空间当中的最优解。

设在一个n维的空间中，由m个粒子组成种群，X={x1,…xi,…xm}，其中第i个粒子的位置为xi={xi1,xi2，…,xin}T,其速度为vi={vi1,vi2,…，vin}T。它目前找到的最优解为pi={pi1,pi2,…，pin}T,种群全局最优解为pg={pg1,pg2,…，pgn}T，按照追随当前最优粒子的原理，粒子xi将按照式(1)和式(2)改变速度和位置[8]。

(1)

(2)

式中：d=(1,2,...，n)；i=(1,2,...,m)；m为种群规模；t为当前进化代数；r1和r2为分布于[0,1]之间的随机数；c1、c2为学习因子。

粒子群优化算法具有收敛速度快，可调参数少，其实现容易、精度高等优势，并且已在解决目标函数优化、自适应控制、组合优化、人工生命等其他实际问题中展示了其优越性。

2密度曲线校正方法理论

2.1Gardner经验公式重构密度曲线

Gardner经验公式建立的是纵波速度与密度的非线性关系如式(3)所示[9]：

(3)

从式(1)可以看出，Gardener经验公式定义的速度与密度的关系呈正比的关系，速度越大，重构的密度曲线也就越大。它的优点是简单、快速。缺点有两方面：①它不是一个普适的方法，并不适用于每个工区；②密度与纵波速度在不同深度上，它们的关系会发生变化，而Gardner经验公式并不能准确反映这种随深度变化关系。

2.2基于粒子群优化算法多元线性拟合校正方法

基于粒子群优化算法的多元线性拟合方法的主要原理是在井眼环境差的层段附近，寻找与该层段具有相似的岩性或物性，且井眼环境好的层段，并把该层段作为参考层，使用该层段受井径影响较小的伽马曲线、声波时差曲线和电阻率曲线建立与密度相关的多元线性拟合模型。其公式见式(4)。

DEN=a×GR+b×log(RD)+c×AC+d

(4)

式中：DEN、GR、RD、AC分别表示表示参考层段密度曲线、伽马曲线、电阻率曲线、声波时差曲线；a、b、c分别表示伽马、电阻率和声波时差在这个多元线性拟合模型中所占的权重；d为拟合系数。

当我们计算这些系数时，应用粒子群优化算法，可以降低建立的线性拟合模型的误差。首先我们输入参考层段的密度、伽马、电阻率、声波时差曲线，随机生成初始的m个粒子，每个粒子的位置为xi={xia,xib,xic,xid}T,计算目标的适应度函数如式(5)所示。

(5)

式中：DENk、GRk、log(RDk)、ACk表示参考层段的密度、伽马、电阻率、声波时差采样点；N表示采样点总个数。

计算每个粒子适应度函数的值，并根据它更新粒子的历史最优位置，直到达到全局最优的位置，最终得到最优的参数a、b、c、d。计算流程见图1。

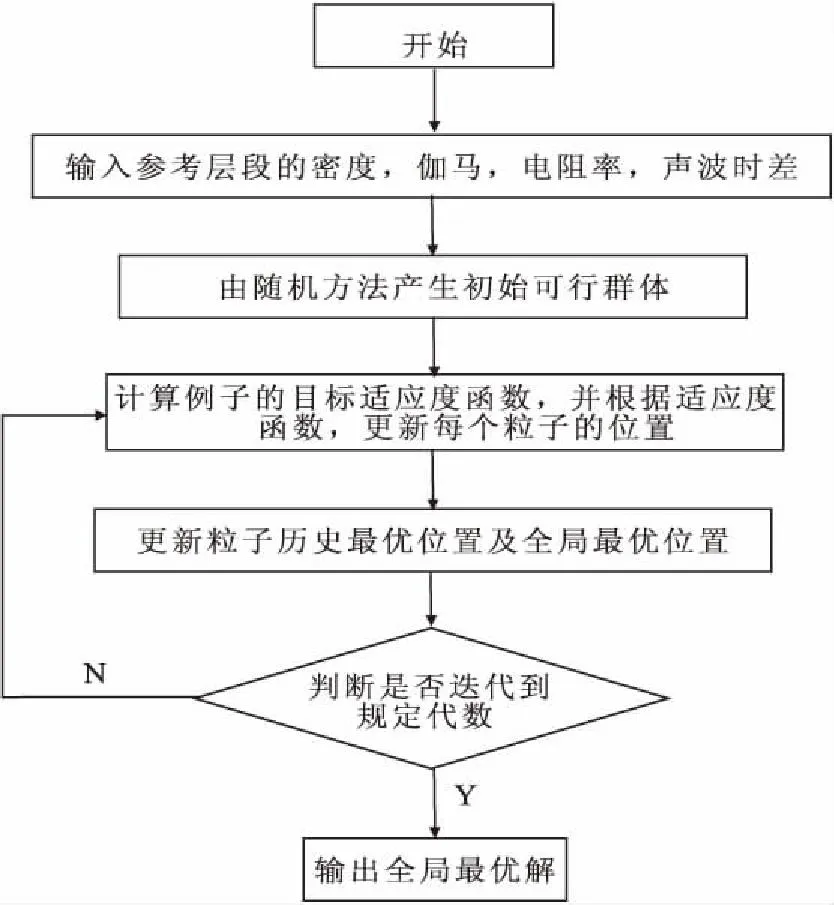
图1　基于粒子群优化算法的多元线性拟合流程Fig.1　Flow chart of multivariate linear fitting based on POS

当求得出参考层的多元线性拟合模型之后，再使用它重构其他层段的密度曲线，其校正公式见式(6)。

DEN′=a×GR+b×log(RD)+c×AC+d

(6)

式中：DEN′表示重构的密度曲线；GR′、RD′和AC′分别表示井眼环境不好的层段的伽马曲线、电阻率曲线和声波时差曲线；a、b、c表示伽马、电阻率和声波时差在已求得的多元线性拟合模型中所占的权重；d为拟合系数。

这里使用这三条测井曲线原因为：①这三种测井曲线受井眼环境的影响相对较小；②对于具有相似的岩性或者相似的物性的不同层段，这三条曲线的测井响应一般具有一致性，例如对于砂岩层段来说，一般为低伽马、高电阻、低声波时差的响应等特征，具有相对的稳定性。

如果只用伽马曲线重构密度曲线，那么对于伽马曲线的质量要求非常高，伽马曲线测量的是地下地层的放射性，可以用来区分砂泥岩。但当地下地层存在有放射性的物质时，或者存在钾长石这类矿物(虽然在岩性上被划分为储层，但它却是高伽马的响应)，仅用伽马曲线重构密度曲线会存在很大的风险。多元线性拟合的方法具有更强的抗干扰性，在该方法中，我们增加了电阻率曲线、声波时差曲线、减小了重构的密度曲线对于单一伽马曲线的质量依赖，提高了重构密度曲线的质量。

3划分密度曲线失真段

在对密度曲线进行校正之前，需要划分出密度曲线失真段。我们可以不对密度曲线做处理，而是直接做合成地震记录，时深转换之后，与井旁地震道作对比。 在目的层附近，寻找与井旁地震道不匹配的层段，查看其所在位置的井径曲线是否扩径，如果该位置的井眼环境不好，再查看这个层段的密度曲线是否出现相对周围层段异常低的值，并结合该层段的岩性资料，确认是否由于岩性的快速变化，而造成密度出现低值，还是由于井径影响的，从而确认失真段。

4在CK井上的应用

川西某地区CK井位于四川盆地川西孝泉—新场构造带，其钻遇的储层为川西海相碳酸岩储层。按照作者提出的多元线性拟合方法原理和步骤：

1)找出密度曲线失真段。具体做法为：直接使用原始的密度曲线，声波时差曲线进行合成地震记录(图2)。由图2可以看出，原始密度曲线总体的质量是不错的，只是在局部井段由于受井间扩径的影响，在扩径段存在一定误差，从而使该扩径井段所在位置对应的合成地震记录的细节特征无法有效地体现出来，但可以看出井旁地震道与合成地震记录大的同相轴基本能够对应起来，但在目标层段无论是反射波能量还是相位特征，合成记录和井旁道不太吻合，井旁地震道与合成地震记录的相关性只有0.59。

2)对比分析测井曲线与井径曲线。有两处比较明显的扩径的地层(红色圈处)，分别命名为1号垮塌处(5 944 m～5 975 m)，2号垮塌处(6 141 m～6 232 m)，这两处地层的密度相对相邻上下地层的密度值来说异常的低。1号垮塌处位于雷口坡组雷4段下部，该处的岩性为灰色微晶白云岩、泥晶白云岩与灰白色硬石膏岩不等厚或等厚互层。该层段的岩性属于高密度的碳酸岩，岩性相似，不会产生密度的快速变化。2号垮塌处位于雷口坡组雷3段中部，该处的岩性为(膏质)微晶白云岩、灰质泥晶白云岩、砂屑白云岩、(云质)微晶灰岩、(含云)微晶灰岩夹少量灰白色石膏岩。其岩性与其相邻的上下的地层相似，也不应该出现密度与剧烈变化。

3)分别用Gardner经验公式和多元线性拟合的方法校正失真层段的密度曲线。Gardner经验公式校正密度曲线：选取与1、2号垮塌处的相同深度的纵波速度曲线，根据Gardener经验公式所定义的纵波速度与密度的非线性关系校正垮塌处的密度。基于粒子群优化算法的多元线性拟合的方法校正密度曲线：根据选取参考层段的原则，与垮塌处有相似的岩性，并且井壁较为平滑。为1号垮塌处选取的参考层段为(5 825 m～5 925 m)，为2号垮塌处选取的参考层段为(6 046 m～6 124 m)，用这两个参考层段里的伽马曲线、声波时差曲线、电阻率曲线分别建立与密度相关的粒子群优化算法的多元线性拟合模型(表1)，设置2 000个随机粒子,每一个粒子是一个四维向量，用[a,b,c,d]T表示，a、b、c、d代表对应的多元线性拟合的权重参数，这些参数刚开始都是随机的，通过与对应的声波时差(AC)，电阻率的对数(log(RD))，伽马(GR)，进行相乘，得到密度数据，再用这个密度数据与原始密度做均方根误差计算。在迭代过程中，所有粒子都进行前面的计算，从中选出均方根误差最低的粒子。然后更新速度公式，进行下一轮循环，寻找均方根误差最小所对应的粒子。重复上面的步骤，直到循环的次数结束或误差收敛，或者连续三次计算的最小的均方根误差的粒子相等，结束循环，最终得到最优粒子，也就是粒子群优化算法的多元线性拟合模型，用这个模型重构各自失真层段的密度曲线。

从图3可以看出，使用Gardner经验公式校正后的密度曲线在①、②号井径垮塌处，比实测的密度曲线有所改进，但还存在明显的低值异常；而基于粒子群优化算法的多元线性拟合校正的密度曲线在这两处曲线变得比较光滑，整个测井段曲线的变化趋势也比较自然，结合该区的岩性变化特征，说明校正的曲线更合理和有效。

为了进一步说明基于粒子群优化算法的多元线性拟合校正的密度曲线的可靠性。我们分别使用Gardner经验公式校正的密度曲线和多元线性拟合校正的密度曲线做合成地震记录，见图4、图5。

如图4所示，校正后的密度曲线所做的合成地震记录与井旁地震道匹配度不高，校正后的合成记录与井旁地震道的相位和能量并没有较好的对应关系，它们之间的相关系数为0.65，相对原始曲线合成记录有一定改善，但T2l4下部对应关系不明显。

表1　基于粒子群优化算法多元线性拟合模型及均方根误差Tab.1　Multivariate linear fitting method based on the PSO and root-mean-square error

从图5可以看出，基于粒子群优化算法的多元线性拟合校正的密度曲线做的合成地震记录与井旁地震道的匹配度较高，校正后的合成记录与井旁地震道的相位和能量具有较好的对应关系，它们之间的相关系数为0.86。特别是T3ml与T2l4之间的波组特征更为明显，与井旁地震道吻合的非常好，而且T2l4的波组特征对应关系也具有较好的对应关系，这说明校正后的曲线明显提高了地震标定的可靠性。

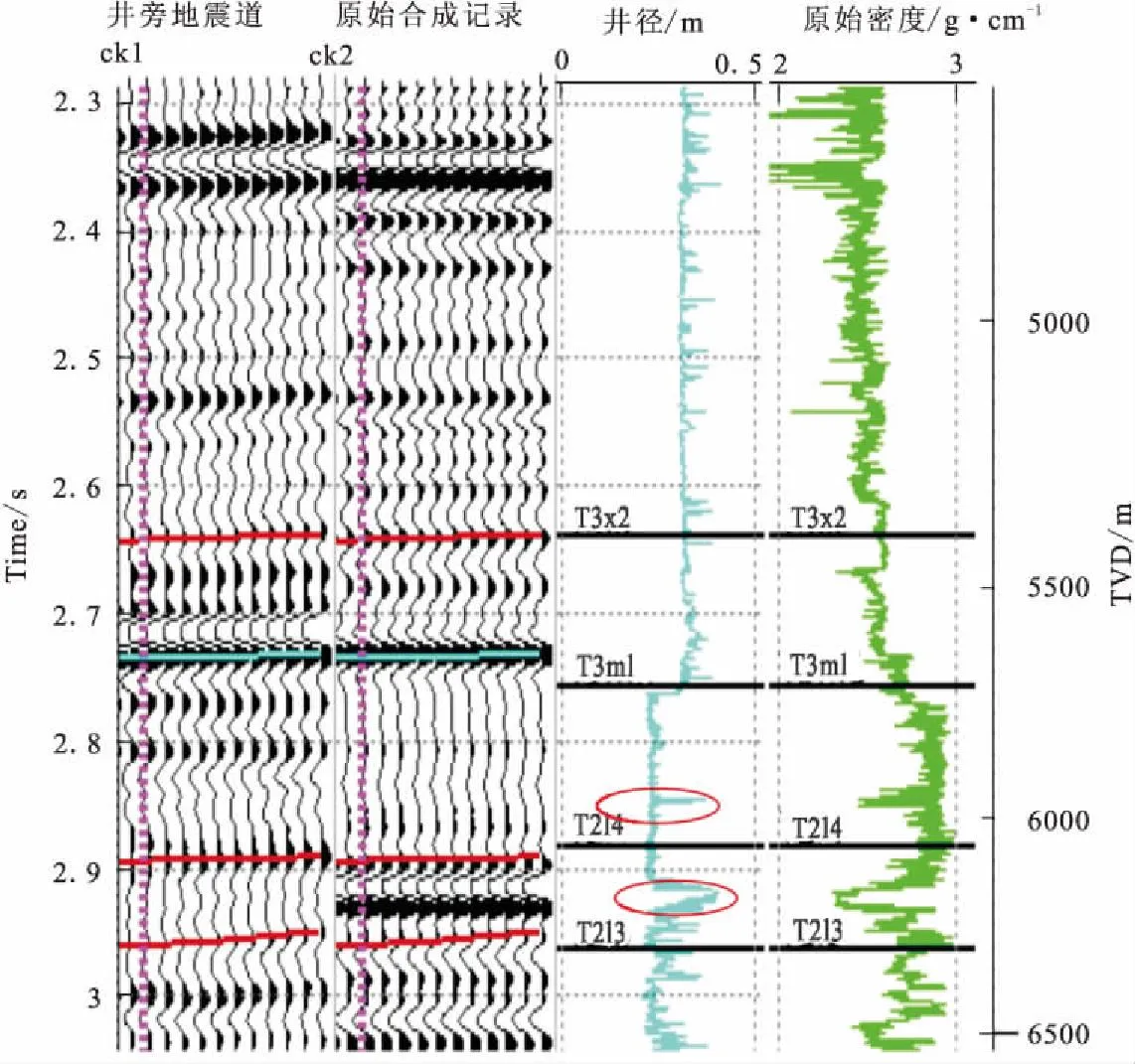
图2　密度曲线不作任何校正的ck1井井震标定Fig.2　The well-seismic calibration based on the original density curve of well ck1

图3　不同的方法校正后的密度曲线对比Fig.3　The comparison of density curves corrected by different methods

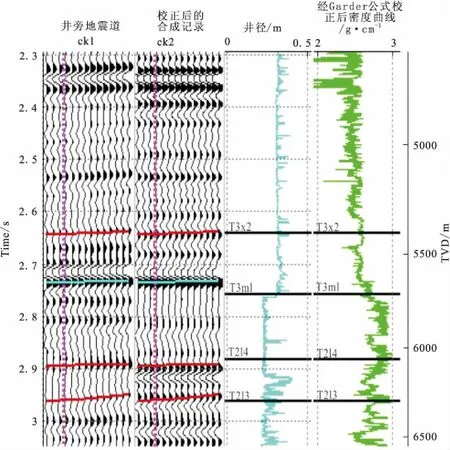
图4　Gardner公式校正密度曲线后的ck1井井震标定Fig.4　The well-seismic calibration based on the density curve，correctedGardner formula,of the well ck1

图5　本方法校正密度曲线后的ck1井井震标定Fig.5　The well-seismic calibration based on the density curve，corrected multivariate linear fitting based on PSO，of the well ck1

5结论

高质量的测井曲线在井震标定中是十分重要的，这是关系到时深转换、岩性反演和储层预测等可靠性的基础资料。将经验公式法和基于粒子群优化算法的多元线性拟合法，应用到校正川西某地CK井的密度曲线校正中。通过原始密度曲线、Gardner计算的密度和基于粒子群优化算法的多元线性拟合的密度曲线对比分析，并定量对比分析了三者的合成记录与原始地震记录的相关系数，认为基于粒子群优化算法的多元线性拟合法有效提高了合成地震记录与井旁地震道的相关性，且相关系数高达0.86。说明该方法能够有效消除井径扩径对密度曲线的影响，为后续工作提供了可靠的密度曲线资料。

参考文献：

[1]黄坚，张红杰，赵卫平，等．测井资料质量控制与评价[J]．工程地球物理学报，2005，2(2)：134-138．

HUANG J,ZHANG H J,ZHAO W P，et al.Quality control and evaluation of well logging data[J].Chinese Journal of Engineering Geophysics,2005，2(2)：134-138．(In Chinese)

[2]马中高，解吉高.岩石的纵、横波速度与密度的规律研究[J].地球物理学进展，2005，20(4)：905-910.

MA Z G,XIE J G.Relationship among compressional wave,shear wave velocities and density of rocks[J].Progress In Geophysics,2005，20(4)：905-910.(In Chinese)

[3]廖茂辉.多元回归方法校正扩径对密度曲线声波曲线的影响[J].物探与化探,2014,38(1):174-179.

LIAO M H.The application of multivariate regression method to the calibration of the influence of hole enlargement on density and acoustic logs [J].Geophysical and Geochemical Exploration,2014,38(1):174-179.(In Chinese)

[4]龚洪林，苏明军，王振卿,等．测井资料环境影响因素分析及实用校正方法研究[J]．物探化探计算技术，2008，30(1)：43-47.

GONG H L,SU M J,WANG Z Q,et al.Analysis of enuironmental influence factors on well data and study on practical correction method[J].Computing Techniques for Geophysical and Geochemical Exploration,2008，30(1)：43-47.(In Chinese)

[5]黄超，兰明杰，秦贞超.多种测井曲线校正方法在塔中顺9井区的应用[J].工程地球物理学报，2014,11(4)：493-497.

HUANG C,LAN M J,QIN Z C.The application of several logging curve correction methods to well shun-9 block of Tazhong area in Tarim basin[J].Chinese Journal of Engineering Geophysics,2014,11(4)：493-497.(In Chinese)

[6]J.KENNEDY，R.EBERHART.Particle Swarm Optimization[C].Proc.In Proceedings of IEEE International Conference on Neurak Networks.1995,1942-1948.

[7]R.EBERHART,J.KENNEDY.A new optimizer using particle swarm theory[C].In Preceeding of 6th International symposium on Micro Machine and Human Science,1995,39-43.

[8]P.J.ANGELINE.Evolutionary optimization versus particle swarm optimazation:philosophy and performance difference[C].Proc.Seventh Annual Conference on Evolutionry Programming,1998,601-610

[9]GARDNER G H F,GARDNER L W,GREGORY A R.Formation velocity and density-the diagnostic basics for stratigraphic traps[J].Geophysics,1974,39(6):770-780.

The particle swarm optimization research and application based on multivariate linear fitting method

HAN Jia-xinga,WU Shi-kaia,TIAN Ren-feia*，LI Jieb，YANG Kuana

(Chengdu University of Technology,a.College of Geophysics, b.Institute of Sedimentary Geology,Chengdu610059,China)

Abstract:In the actual logging,density curve is the most vulnerable to be influenced by hole enlargement.In order to eliminate the influence,the particle swarm optimization is introduced to the multivariate linear fitting method.Particle swarm optimization algorithm is used to optimizing the objective function,which is the intelligent evolutionary algorithm with adaptive control.In this paper,building the multivariate linear fitting model based the particle swarm optimization with some logging curves(such as gammar ray,resistivity and acoustic) ,which is affected relatively small by the borehole environment in the reference layer having a level borehole and the same lithology with the position in the bad bore environment.Then we use this model to reconstruct the density curve in the layer where the borehole is enlarging.Finally,the reconstructed density curve compares with original density curve,the density curve calculated by gardner formula.The research results show that the correlation coefficient between the seismic traces near the well and the synthetic seismic record using the density reconstructed by the multivariate linear fitting methods reached 0.84.It indicated that the proposed multivariate linear fitting method can effectively improve the quality of density logging curves.

Key words:PSO;multivariate linear fitting;bore expanding;correction density

收稿日期：2015-08-14改回日期：2015-11-04

基金项目:国家自然科学基金(41304080，41274128，41404102)

作者简介：韩家兴(1991-)，男，硕士，主要从事地震资料解释、储层预测等方面研究，E-mail：hjx5309@163.com。*通信作者：田仁飞(1983-)，男，副教授，研究方向为石油地球物理勘探，E-mail：tianrenfei08@cdut.cn。

文章编号：1001-1749(2016)02-0212-07

中图分类号：P 631.4

文献标志码：A

DOI：10.3969/j.issn.1001-1749.2016.02.11