k-kL两方程湍流模型的改进及验证研究

李广佳，李喜乐，张强，郝海兵，李典

(1.中国航天空气动力技术研究院 第十一总体设计部，北京　100074)

(2.西北工业大学 航空学院，西安　710072)

(3.中国航空计算技术研究所 第七研究室，西安　710068)

k-kL两方程湍流模型的改进及验证研究

李广佳1，李喜乐1，张强2，郝海兵3，李典3

(1.中国航天空气动力技术研究院 第十一总体设计部，北京100074)

(2.西北工业大学 航空学院，西安710072)

(3.中国航空计算技术研究所 第七研究室，西安710068)

摘要：提高湍流数值模拟的准确性，从而明确湍流模型对数值模拟结果的影响具有重要的意义，应用K.S.Abdol-Hamid给出的尺度自适应k-kL两方程模型封闭RANS方程，并修改von Karman长度尺度的限制方法，通过平板、翼型、后台阶等流动的模拟，考察k-kL模型在湍流模拟中的准确性，及其反映主要流动特征的能力和网格收敛性，并对影响流动模拟准确性的因素进行讨论。结果表明：改进长度尺度限制之后的k-kL两方程模型无论是对附着流动还是分离流动都可以给出比较准确的结果。

关键词：k-kL两方程湍流模型；RANS；von Karman长度尺度

0引言

A.N.Kolmogorov于1942年提出的两方程湍流模型是研究所有基于统计平均的湍流模型的基础。两方程湍流模型的概念反映了湍流研究的基本思想，即在平均流动中模拟湍流效应需要两个相互独立的湍流尺度变量，这两个湍流尺度可以通过各自的输运方程求解给出。此外，两方程湍流模型也是其他更高阶湍流模型的基础和核心，例如雷诺应力模型、显式代数应力模型或者其他基于非线性应力-应变关系的湍流模型。即使只采用涡粘系数作为唯一变量的一方程湍流模型(例如SA湍流模型[1])，也可以在平衡假设(Equilibrium Assumptions)的基础上，从两方程模型推导而来。在一方程湍流模型中，平衡假设认为湍流时间尺度与剪切应变率成反比[2]，因此不需要第二个尺度方程。

在目前所有的两方程湍流模型中，第一个湍流尺度方程几乎都采用湍流脉动动能k方程。只需要对湍流扩散项(Turbulent Diffusion)进行建模，从而可以降低建模的难度。至于第二个湍流尺度方程，目前发展了很多[3]，最常见的是ε和ω方程。尽管第二个湍流尺度方程(例如ε方程)可以通过严格推导得到准确的形式，但鲜有实际应用。准确的形式中包含更复杂和更高阶的关联项，对于这些项目前只能给出量级大小估计[4]，难以采用逐项建模实现，因此实际应用中的ε和ω方程通过量纲分析或者直观物理分析得到，并采用与k方程类似的形式。

针对第二个湍流尺度，J.C.Rotta[5]采用逐项建模的方法给出了一种(kL)方程，其中的L指的是湍流的积分长度尺度，k是湍流脉动动能。J.C.Rotta提出的kL方程源项中，包含速度的三阶导数项，这在实际应用存在诸多问题，限制了其应用[6]。F.R.Menter等[7-9]采用二阶速度导数的合理形式取代三阶速度导数项，表明采用速度二阶导数项后，k-kL方程可以自动满足壁面对数律，并且使模型可以自动调整湍流模拟尺度以满足复杂多尺度湍流结构模拟的需求，而无需像传统RANS方程耗散掉。在F.R.Menter修改的基础上，K.S.Abdol-Hamid等[10-11]给出了完整形式的k-kL两方程模型，并对模型所用的常数进行了标定。

目前，国内对于基于湍流积分长度尺度的湍流模型，未见报道，因此本文对尺度自适应k-kL两方程模型开展初步的研究。为了提高k-kL模型的数值稳定性和准确性，修改von Karman长度尺度的限制方法；通过对典型流动的模拟，考察改进后的k-kL模型在定常湍流模拟中的准确性、捕捉主要流动特征的能力及其网格收敛性，并对影响流动模拟的因素进行讨论。

1k-kL湍流模型控制方程

守恒形式的k-kL两方程湍流模型控制方程可以写为

(1)

(2)

Lvk为von Karman长度尺度，为了避免长度尺度之比(L/Lvk)过大或者过小，对Lvk取值限制如下：

(3)

不同的rPD对应不同的von Karman长度尺度限制方法。F.R.Menter根据附着流动湍流生成和耗散之比约等于1，取rPD=1。但是，当流动有分离时rPD却不等于1，于是K.S.Abdol-Hamid定义

(4)

采用K.S.Abdol-Hamid的定义可以极大地改善k-kL模型在分离区的模拟精度，但是对全流场都采用此限制也不妥，因此把rPD修改为

(5)

从而使Abdol-Hamid的限制只在rPD小于等于1时的流动区域有效，而在其他流动区域自动成为Menter的限制。模型中各常数取值如下：ζ1=1.20，ζ2=0.97，ζ3=0.13，σk=1.00，σφ=1.00，κ=0.41，Cμ=0.09，Cl1=10.00，Cl2=1.30，Cd1=4.70。

2数值计算方法及边界设置

流动控制方程基于多块结构网格采用基于格心的二阶有限体积法进行空间离散，其中无粘项采用Roe-FDS格式离散，粘性项采用中心差分近似。但在湍流模型无粘项的离散中仅采用一阶迎风格式。RANS方程和湍流模型方程采用主对角占优DDADI格式以松耦合的方式进行隐式时间推进。为了更加快速地得到定常解，采用当地时间步长和多重网格加速收敛技术。

湍流模型变量k和kL在物面均取0，自由来流条件只需保证流动能自动转捩为全湍流。

文中所有验证算例，若无特殊说明，均采用式(5)的限制方法，并且结果均与理论或实验数据进行对比分析。

3算例与分析

3.1网格收敛性

为了考察k-kL模型的网格收敛性，分别在545×385(极密网格，Super-Fine)，273×197(密网格，Fine)，137×97(中等密度网格，Medium)，69×49(稀疏网格，Coarse)，35×25(极稀疏，Tiny-Coarse)从密到疏的五套网格上，计算Ma为0.2、单位平板长度Re为5×106的平板附面层(各网格中的平板长度取为x/c=2.00)的摩擦系数。不同密度网格上沿平板的摩擦系数与理论值的比较如图1所示。

图1　不同密度网格计算的摩擦系数比较

从图1可以看出：密网格和极密网格上的计算结果差别较小、几乎重合，在中等密度网格上的计算结果与密网格和极密网格上的差别已经很小，而在稀疏网格和极稀疏网格上的计算结果与网格和极密网格上的差别较大，并且网格越稀疏，计算结果越偏离理论解；受附面层粘性底层建模项的影响(k和kL方程右端第三项)，在平板前缘的转捩间断比其他两方程模型更为明显，并且转捩点的位置随着网格的加密前移，更接近平板前缘。

不同密度网格上计算的x/c=0.97处摩擦系数的比较如图2所示。

图2　计算摩擦系数随网格密度变化

从图2可以看出：随着网格的加密，摩擦系数变化趋势与CFL3D和FUN3D在同系列网格上用SSTk-ω模型所得变化趋势一致[12]，并且在最密网格上的摩擦系数基本相同。

3.2y+对计算结果的影响

为了考察y+对计算结果的影响，首先在x/c=1.00长的平板上生成65×97的网格(流向网格节点总数65，物面法向网格节点总数97)，然后通过调整物面第一层网格到物面的距离和物面法线方向的网格增长率，得出六套网格。在Ma为0.2、单位平板长度Re为6×106时，k-kL模型在不同网格上计算的平均y+从小到大依次约为0.020，0.220，0.505，1.150，2.290，4.600。在不同y+时计算的摩擦系数与理论值的比较如图3所示。可以看出：当y+=0.220，0.505，1.150，2.290时计算的摩擦系数沿平板变化曲线接近；当y+进一步增加或者减小时，平板摩擦系数都会变小，进一步偏离理论解。

图3　不同y+计算的摩擦系数比较

为了进一步说明y+对计算结果的影响，给出x/c=0.79处不同y+时计算摩擦系数的比较，如图4所示。

图4　x/c=0.79处不同y+计算的摩擦系数

从图4可以看出：当y+分别为0.220，0.505，1.150时计算所得摩擦系数几乎相等；y+=2.290时的结果相比前三种计算值略小，但差别小于0.1个阻力单位(1×104为1阻力单位)；y+=0.020和4.600时的结果与其他结果差别较大，接近甚至超过0.25个阻力单位。结果表明：k-kL模型与其他两方程模型相同，为了保证附面层模拟的精度，y+约等于1最优。

3.3不同湍流初始条件的影响

分别计算两种湍流初始条件下的平板附面层，如表1所示。

表1　Ma=0.2时不同的湍流初始条件

在两种湍流初始条件下，不同密度网格上计算x/c=0.97处的摩擦系数，如图5(a)所示，可以看出：各网格上计算结果几乎相同，差别可以忽略不计。在两种湍流初始条件下，中等密度网格上的摩擦系数如图5 (b)所示，摩擦系数曲线也几乎处处重合。

(a) x/c=0.97摩擦系数

(b) 不同湍流条件下的摩擦系数

综上所述，只要给定的自由来流湍流度Tu和μt/μ∞能够保证流动转捩为全湍流，k-kL模型的计算结果与自由来流湍流条件无关，即k-kL模型对自由来流的湍流条件并不敏感。

3.4不同长度尺度限制的影响

本节验证算例考虑无分离平板流动、NACA4412翼型粘性绕流和后台阶流动。

在无分离的平板流动中，采用式(5)的限制和采用Menter的限制计算的摩擦阻力系数和速度型几乎完全相同，如图6所示。

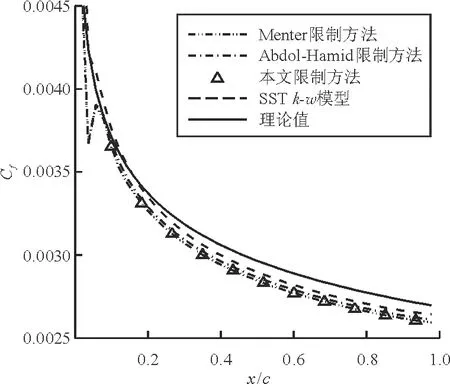
(a) 摩擦系数

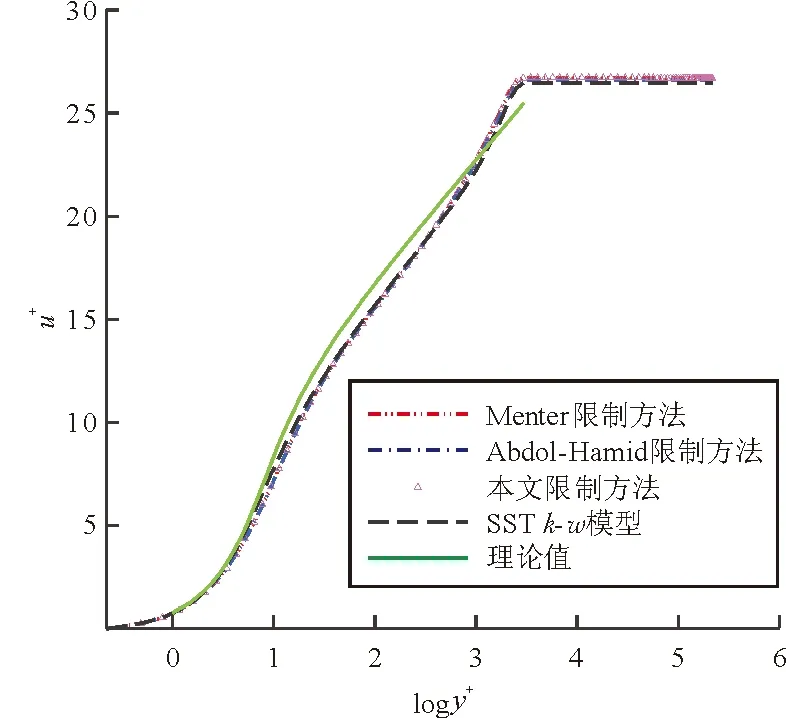
(b) 速度型

从图6可以看出：在无分离或远离物面的区域，式(5)采用的是Menter的限制；与采用其他两种限制方法相比，采用Abdol-Hamid的限制会使计算的摩擦系数略微增加、在离开物面相同位置处计算的速度稍偏大，但差别不大。

为了进一步说明式(5)的修改在小分离流动中的效果，对NACA4412翼型粘性绕流进行模拟。计算的翼型表面压力分布及上表面六处站位的速度型与实验值的比较如图7所示，前三处站位在分离之前，后三处站位处于分离区。

(a) 翼型表面压力分布

(b) 在x/c=0.620处的速度型

(c) 在x/c=0.675处的速度型

(d) 在x/c=0.731处的速度型

(e) 在x/c=0.786处的速度型

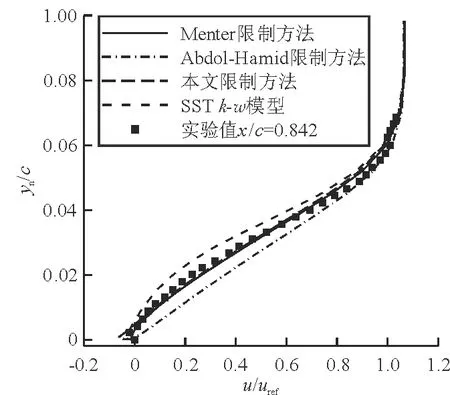
(f) 在x/c=0.842处的速度型

(g) 在x/c=0.897处的速度型

(h) 在x/c=0.953处的速度型

从图7(a)可以看出：k-kL模型给出的压力分布在上表面后缘分离区之前均略高于SST模型，在分离区内，比SST模型略低。

从图7(b)～图7(h)可以看出：采用式(5)限制方法的k-kL模型所给出的速度型，在前三个站位以及后三个站位的附面层外部区域，与采用Menter的限制给出的结果接近，而在分离区内靠近物面区域，与采用Abdol-Hamid的限制给出的结果类似；采用式(5)限制方法给出的结果在无分离区与SST模型相当，但在分离区的结果要优于SST模型，与实验值更为吻合。

综上所述，不管有无分离，采用式(5)的限制方法可以给出最为准确的数值模拟结果。

针对后台阶流动算例，生成四块网格129×129，49×129，193×225，65×225，离开物面第一层网格的平均y+约为0.887。在该网格上，采用不同von Karman长度尺度限制方法计算后台阶下壁面的摩擦系数，如图8所示。可以看出：采用Menter的限制方法，计算结果不收敛，流动是非定常的，而采用Abdol-Hamid和式(5)进行计算，均可以得到准定常的收敛结果，并且给出的下壁面摩擦系数差别不大，与实验值吻合良好，k-kL模型的结果要略好于SSTk-w模型。

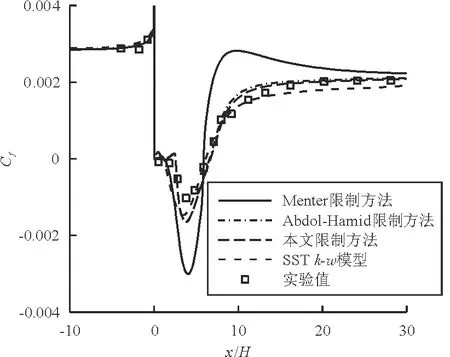
图8　后台阶下壁面摩擦系数对比

4结论

(1)k-kL模型具有优异的网格收敛性；为了准确求解附面层，物面第一层网格的平均y+约为1的量级最优。

(2)k-kL模型对湍流自由来流条件不敏感，只需保证流动能转捩为全湍流即可。

(3) 采用式(5)的von Karman长度尺度限制方法，不管流动是否有分离，k-kL模型都可以给出较为准确的结果。

参考文献

[1] Spalart P R, Allmaras S R. A one-equation turbulence model for aerodynamic flows[J]. La Recherche Aerospatialen, 1994, 1: 5-21.

[2] Menter F R. Eddy viscosity transport equations and their relation to thek-εmodel[J]. Journal of Fluids Engineering, 1997, 119: 876-884.

[3] Kantha L H. The length scale equation in turbulence models[J]. Nonlinear Processes in Geophysics, 2004, 11(1): 83-97.

[4] Temmerman L, Leschziner M A. Large eddy simulation of separated flow in a streamwise periodic channel constriction[C]. Stockholm: 2nd Symposium on Turbulence and Shear-Flow Phenomena, 2001.

[5] Rotta J C. Statistische theorie nichthomogener turbulenz[J]. Zeitschrift für Physik, 1951, 129: 547-572.

[6] Rodi W. Turbulence modelling for boundary layer calculations[C]. Göttingen: Springer, IUTAM Symposium One Hundred Years of Boundary Layer Research, 2004.

[7] Menter F R, Egorov Y. The scale-adaptive simulation me-thod for unsteady turbulent flow predictions(Part 1): theory and model description[J]. Flow Turbulence Combust, 2010, 85: 113-138.

[8] Menter F R, Egorov Y. The scale-adaptive simulation me-thod for unsteady turbulent flow predictions(Part 2): application to complex flows[J]. Flow Turbulence Combust, 2010, 85: 139-165.

[10] Abdol-Hamid K S. Assessmants ofk-kLturbulence model based on Menter’s modification to Rotta’s two-equation model[J]. International Journal of Aerospace Engineering, 2015(1): 1-18.

[11] Abdol-Hamid K S. Assessments of a turbulence model based on Menter’s modification to Rotta’s two-equation model[C]. AIAA-2013-0341, 2013.

[12] Chris Rumsey. Turbulence modeling resource[EB/OL].(2015-11-05)[2016-04-20].http:∥turbmodels.larc.nasa.gov.

Improvement and Validation ofk-kLTwo-equation Turbulence Model

Li Guangjia1, Li Xile1, Zhang Qiang2, Hao Haibing3, Li Dian3

(1.The Eleventh Design Department, China Academy of Aerospace Aerodynamics， Beijing 100074， China)

(2.School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China)

(3.No. 7 Department, Aeronautical Computing Technique Research Institute, Xi’an 710068, China)

Abstract:It is of important significance to improve the accuracy of turbulent flow simulations, and identify the effects of turbulence model on simulation results. The scale adaptive k-kL two-equation turbulence model constructed by K.S.Abdol-Hamid is applied to close RANS equations and assessed. A modification to the upper limit in von Karman length scale is proposed. Some factors effecting simulation accuracy are also discussed. A number of test cases including flat plate case, airfoil case and backward facing step case are run to demonstrate the accuracy of this model and its capability to resolve important flow features and grid convergence. Test results show that this turbulence model is superior or at least comparable to other two-equation turbulence models in simulating either attached or separated turbulent flows.

Key words:k-kL two-equation turbulence model; RANS; von Karman length scale

收稿日期：2016-04-20；修回日期：2016-05-10

通信作者：李喜乐,lxl1027@163.com

文章编号:1674-8190(2016)02-209-07

中图分类号：V211

文献标识码：A

DOI：10.16615/j.cnki.1674-8190.2016.02.011

作者简介：

李广佳(1979-)，男，硕士，高级工程师。主要研究方向：计算流体力学、飞行器设计。

李喜乐(1985-)，男，博士，工程师。主要研究方向：计算流体力学、设计空气动力学。

张强(1979-)，男，博士，副教授。主要研究方向：理论与计算流体力学。

郝海兵(1981-)，男，博士，高级工程师。主要研究方向：理论与计算流体力学、气动优化设计。

李典(1986-)，男，博士，工程师。主要研究方向：计算流体力学。

(编辑：赵毓梅)