利用遗传算法求解圆排列问题①

徐小平,朱秋秋,邰会强(西安理工大学 理学院,西安 70048)(西安理工大学 机械与精密仪器工程学院,西安 70048)



利用遗传算法求解圆排列问题①

徐小平1,朱秋秋1,邰会强2
1(西安理工大学 理学院,西安 710048)
2(西安理工大学 机械与精密仪器工程学院,西安 710048)

摘 要:圆排列问题是一个典型的组合优化问题,也是一个NP完全问题.遗传算法是根据自然界生物学进化而发展起来的一种进化方法,其具有简单、易行、抽象性与鲁棒性特征,已成功地解决了许多工程优化问题.给出基于改进遗传算法给出求解圆排列问题的新方法.首先,分析了圆排列问题与旅行商问题之间的关系.然后,将圆排列问题转化为旅行商问题.接着,利用所给改进遗传算法进行了求解.最后,在仿真实验中,与已有算法进行了比较,结果表明,所给算法是一种能够简单有效地求解圆排列问题的新方法.

关键词:圆排列问题; 组合优化; 遗传算法; 进化算法

圆排列问题是一个典型的组合优化问题,也是NP-hard问题[1].它不仅具有组合优化问题的典型特征,并且其描述简单.因此,许多学者将圆排列问题的算例作为算法研究的公共实例[2,3].目前,圆排列研究的最多的问题是如何求解最小长度,即就是说,要求从n个圆的所有排列中找出有最小长度的圆排列.它有很强的应用背景,比如包装问题[4]、农机作业优化[5]、物流配送问题[6]等等问题,都可以被转化为圆排列问题.因此,对圆排列问题的研究具有重要的现实意义.

遗传算法(Genetic Algorithm,GA)是一种模仿生物自然进化过程的、自适应启发式的全局优化算法[7].它不存在求导和函数连续性的限定、具有内在的隐并行性和优秀的全局寻优能力,能自动获取和指导优化的搜索空间,自适应地调整搜索方向,且求解问题时仅需要很少的辅助信息,容易与其他领域的知识相结合,所以在自动组卷问题[8]、车辆路径问题[9]、储层识别技术[10]、本体映射技术[11]等领域已得到了广泛的应用.当然,它也为解决圆排列问题提供了一种有效工具.

本文尝试利用GA对圆排列问题进行求解.首先,叙述了圆排列问题和旅行商问题之间的关系.接着,将圆排列问题转化为旅行商问题.然后,利用一种改进遗传算法给出了圆排列问题的有效求解.在选择、交叉和变异之后,引进连续多次的进化逆转操作,有效的加快了算法的收敛速度.最后,通过仿真实验结果说明该方法是有效的.

1　问题的描述

实际工程中经常涉及到把一个矩形钢板切割成半径不等的圆,尽可能节省材料的圆排列问题.即就是说,给定n个大小不等的圆c1,c2,…,cn,现要将这n个圆排进到一个矩形框中,并且要求与矩形的底边相切.本文首先将圆排列问题转化为旅行商问题,然后用改进GA对其进行求解.

已知圆ci的半径ri(i=1,2,…,n),假如排列方式为i1,i2,…,in,则长度为

旅行商问题具体是指有n个城市,城市i,j之间的距离为dij,一个旅行商从城市1出发到其他每个城市去一次且只去一次,最后回到城市1,旅行商问题要求从2～n个城市的所有排列中找出总路线最短的路线.

假设把1～n个圆分别放置在1～n个城市中,城市i和城市j之间的距离dij(i= 1,2,L ,n;j=1,2,…,n)为.再增加一个城市0,它与城市j的距离d0j(j=1,2,…,n)为d0j=rj.因此,圆排列问题与旅行商问题等价[12].也就是说,一个旅行商从城市0出发到其他每个城市去一次且只去一次,最后回到城市0,而旅行商问题要求从1～n个城市的所有排列中找出总路线最短的路线.所以,求解圆排列问题就可以变为求解旅行商问题.

2　改进的随机松弛法求解TSP

GA由美国Michigan大学J.Holland教授于1975年提出[14],它通过模拟生物进化过程搜索最优解,且与传统优化算法相比,其具有高鲁棒性、全局搜索性、内在并行性等优点[15].因此,其受到人们的普遍关注,且已被广泛应用到各个领域.

GA的基本步骤如下:

步骤1.随机产生初始种群,并设置好初始的参数.

步骤2.进行迭代.

步骤3.执行选择算子,选择优良的个体,并淘汰适应度低的个体.

步骤4.执行交叉算子.

步骤 5.执行变异算子.

步骤 6.计算每个个体的适应度.

步骤 7.如果逻辑条件满足,结束迭代.否则,转到步骤2.

3　改进遗传算法求解圆排列问题

本文针对基本遗传算法易陷入局部极小值,较难快速稳定地找到最优值的缺点,在选择、交叉和变异之后,引进连续多次的进化逆转操作对遗传算法进行改进,使算法的每一代都能从父代继承更多的基因,从而提高算法的局部搜索能力.改进后的算法可以跳出局部极小值,快速稳定地寻找到最优值.这样就能够有效的加快算法的收敛速度,同时使得寻优结果会更加令人满意.以下为利用改进GA求解圆排列问题的实现步骤.

Step 1.编码: 采用整数排列编码方法.对于n个圆的排列问题,染色体分为n段,其中每一段为对应圆的编号,比如,对10个圆的排列问题{1,2,3,4,5,6,7,8,9,10},则|1|10|2|4|5|6|8|7|9|3就是一个合法的染色体.

Step 2.种群初始化: 在完成染色体编码以后,必须产生一个初始种群作为初始解,所以首先需要决定初始化种群的数目.初始化种群的数目一般根据经验得到,且一般情况下种群的数量视圆规模的大小而决定.

Step 3.确定适应度函数: 假设k1|k2|…|ki|…|kn|为一个采用整数编码的染色体,为圆ki到圆kj的距离,则该个体的适应度函数为

即就是说,适应度函数为恰好走遍n个圆的距离的倒数.优化的目标就是选择适应度函数值尽可能大的染色体,适应度函数值越大的染色体越优质,反之越恶劣.

Step 4.选择操作: 从旧群体中以一定概率选择个体到新群体中,个体被选中的概率跟适应度函数值有关,个体适应度值越大,被选中的概率越大.

Step 5.交叉操作: 采用部分映射杂交,确定交叉操作的父代,将父代样本两两分组,每组重复以下过程(假定圆的个数为10).

Substep 1.产生两个[1,10]区间内的随机整数r1和r2,确定两个位置,对两位置的中间数据进行交叉,比如,当r1=4,r2= 7时

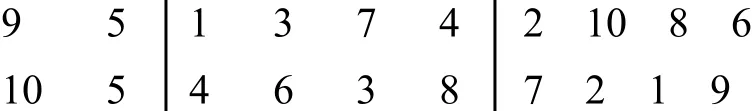
对其交叉后为

Substep 2.交叉后,同一个个体中有重复的圆的编号,不重复的数字保留,有冲突的数字(带*位置)采用部分映射的方法消除冲突,即就是,利用中间段的对应关系进行映射,其结果为

Step 6.变异操作: 变异策略采取随机选取两个点,将其对换位置.产生两个[1,10]范围内的随机整数r1和r2,确定两个位置,将其对换位置,比如,当r1=4,r2= 7时,

对其变异后为

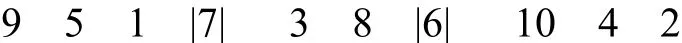
Step 7.进化逆转操作: 为改善遗传算法的局部搜索能力,在选择、交叉和变异之后引进连续多次的进化逆转操作.这里的“进化”是指逆转算子的单方面性,即就是说,只有经过逆转后,适应度值有所提高的才接受下来,否则逆转无效.即产生两个[1,10]区间内的随机整数r1和r2,确定两个位置,将其对换位置,比如,当r1=4,r2= 7时

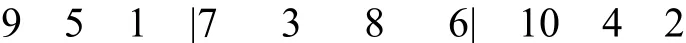
对其进化逆转后为

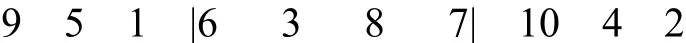
对每个个体进行交叉变异,然后带入适应度函数进行评估,选择出适应度值大的个体进行下一代的交叉和变异以及进化逆转操作.

Step 8.判断操作: 如果满足设定的最大遗传代数的话,则终止程序; 否则,转到Step 3.

5　仿真实验

本文提出的进化逆转操作,对于圆排列问题,就调整前后引起的圆排列圈的长度变化而言,用于最细微的调整,因而局部优化的精度较高.为了说明本文所给方法的合理性和可行性,这里考虑了对当圆排列问题n取30,50,100,ri= i( i= 1,2,…,n).利用文中所给改进GA算法对该问题分别进行了求解,并且算法参数的设置均相同,具体如下表1所示.

表1　设置控制参数

当n取30时,首先,随机选择种群中的一个初始随机路线为 19→21→24→10→18→16→15→22→29 →3→6→2→8→30→20→17→27→25→12→13→5→2 8→9→7→11→14→1→26→4→23.

然后,经计算得到的初始随机路线的总距离为836.8342.最后,利用所给方法进行一次求解时的相应随机路线,优化过程和最优路线分别如图1,图2和图3所示.

这样,得到的最优路线为18→12→20→10→22→8→24→6→26→4→28→2→30 →1→29→3→27→5→25→7→23→9→21→11→19→1 3→17→15→16→14 .

此时,最优路线的总距离为750.9867,算法的运行时间为0.25s.

图1　随机路线

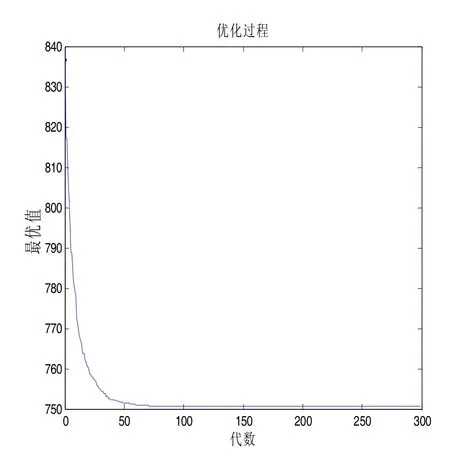
图2　优化过程

图3　最优路线

当n取50时,首先,随机选择种群中的一个初始随机路线为27→16→45→31→30→47→22→8→48→

15→38→44→35→28→33→26→42→24→20→36→2 →50→14→19→21→37→1→18→6→43→46→34→3 2→3→40→10→9→17→5→49→29→41→25→12→1 1→7→39→13→23→4.

然后,经计算得到的初始随机路线的总距离为2253.9.最后,利用所给方法进行一次求解时的相应随机路线,优化过程和最优路线如图4,图5和图6.

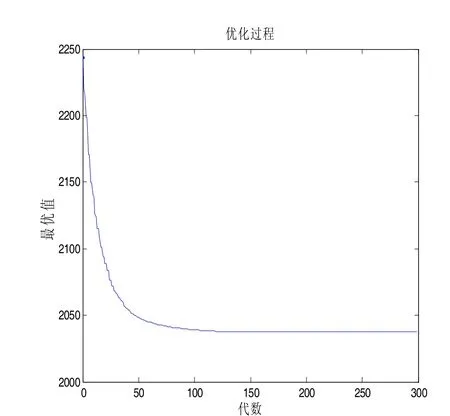
图4　随机路线

图5　优化过程

图6　最优路线

这样,得到的最优路线为30→20→32→18 →34→16→36→14→38→12→40→10→42→8→44→6 →46→4→48→2→50→1→49→3→47→5→45→7→43 →9→41→11→39→13→37→15→35→17→33→19→3 1→21→29→23→27→25→26→24→28→22.此时,最优路线的总距离2038.1,算法的运行时间0.48s.

当n取100时,首先,随机选择种群中的一个初始随机路线为37→65→35→67→50→51→49→53→47 →55→45→57→43→59→41→61→39→63→33→69→31→71→29→73→27→75→25→77→23→79→21→81 →19→83→17→85→15→87→13→89→11→91→9→9 3→7→95→5→97→3→99→1→100→2→98→4→96→6→94→8→92→10→90→12→88→14→86→16→84→18→82→20→80→22→78→24→76→26→74→28→72 →30→70→32→68→34→66→36→64→38→62→40→60→42→58→44→56→46→54→48→52.

然后,经计算得到的初始随机路线的总距离为8007.5.最后,利用所给方法进行一次求解时的相应随机路线,优化过程和最优路线分别如图7,图8和图9所示.

这样,得到的最优路线为50→51→49→53→47→55→45→57→43→61→37→63→39→62→38→65→35 →67→33→69→31→71→29→73→27→75→25→77→23→79→21→81→19→83→17→85→15→87→13→89 →11→91→9→93→7→95→5→97→3→99→1→100→2→98→4→96→6→94→8→92→10→90→12→88→14 →86→16→84→18→82→20→80→22→78→24→76→26→74→28→72→30→70→32→68→34→66→36→64 →41→60→40→59→42→58→44→56→46→54→48→52.此时,最优路线的总距离为8004.4,算法的运行时间为0.89s.

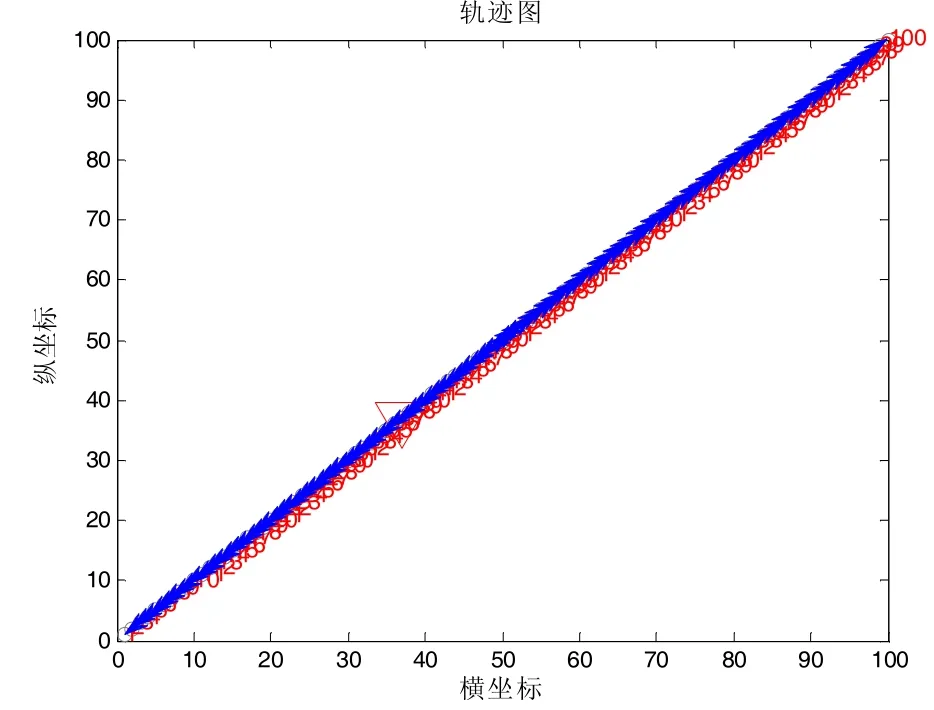
图7　随机路线

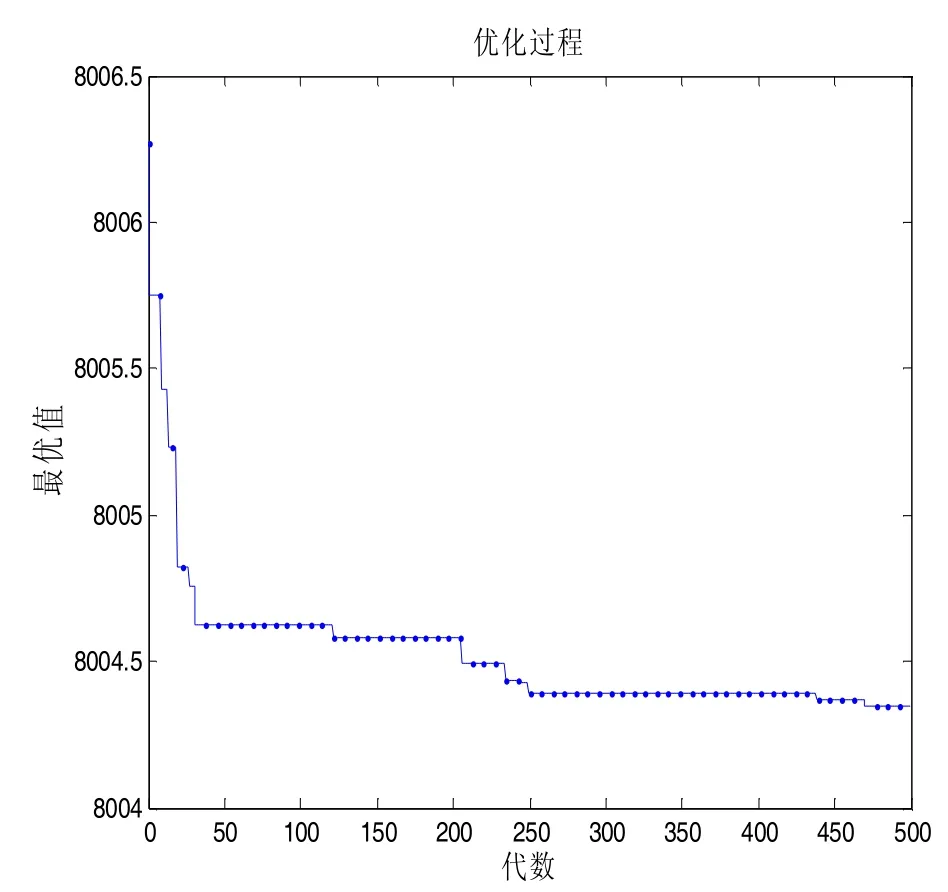
图8　优化过程

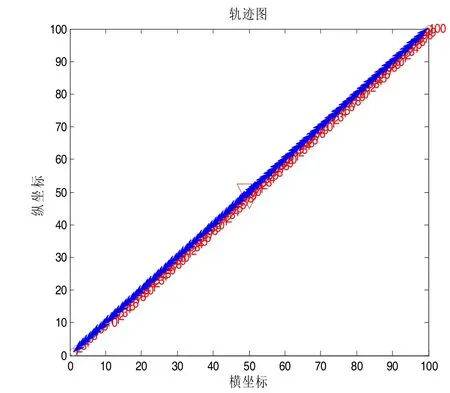
图9　最优路线

为了进一步说明本文方法(即利用改进GA)的有效性,对上述n取30,50和100时,利用本文方法分别进行多次求解后,将其结果的平均值、最好解、最差解和平均所用时间均罗列在表2中.并且分别利用基本GA和文献[12]中的蚁群模拟退火算法分别对n取30,50和100进行多次求解,其相应结果也罗列在表2 中.

表2　实验结果

30 　770.43 　758.73 　777.79 　0.28 50 　2045.6 　2038.1 　2059.91 　0.55基本GA 100 　8032.6 　8024.8 　8076.0 　1.01 30 　765.78 　750.75 　770.459 　0.67 50 　2041.5 　2037.5 　2045.5 　0.98文献[12] 100 　8023.1 　8019.8 　8049.7 　1.05 30 　787.469 784.417 792.951 　0.0546 50 　2224.82 2218.76 2238.61 　0.2815文献[13] 100 8843.46 8821.88 　8867.7 　2.2734

从以上结果可以看出,利用文中所提方法得到的结果优,用时较短,而且随着n的增大,优势更为明显.从而可以看出文中所给方法是合理有效的.

6　结束语

本文给出了基于一种改进遗传算法求解圆排列问题的新方法.首先,将圆排列问题与旅行商问题进行了对比分析.然后,将圆排列问题转化为旅行商问题,从而得出一个相应的组合优化问题.接着,利用具有良好收敛性的改进遗传算法给出了该问题的求解.最后,利用仿真结果说明了所给方法是可行的.

参考文献

1Applegate DL,Bixby RE,Chvatal V,et al.The Traveling Salesman Problem: A Computational Study.Princeton: Princeton University Press,2011.

2麻存瑞,马昌喜.不确定旅行商问题的鲁棒模型与算法.计算机应用,2014,34(7):2090–2092.

3王庆,刘学鹏.基于流水算法的旅行商问题求解.预测,2014,33(1):65–69.

4杨金勇,宋海洲.圆排列包装问题最优解解析.华侨大学学报,2013,34(2):221–224.

5杨巍,刘占良.农机作业路径优化的研究—基于旅行商问题新算法.农机化研究,2014,(6):55–57.

6乐国友.基于节约算法的旅行商问题配送线路优化.物流技术,2013,33(2):241–244.

7Holland JH.Adaptation in Natural and Artificial Systems.Ann Arbor: University of Michigan Press,1975.

8刘召华,李建良.自动组卷中简单遗传算法的应用.卷宗,2014,(3):186.

9刘俐.基于遗传算法的车辆路径问题研究.中国电子商务,2014,(4):81.

10李铁军,薛玲,郭大立,杜国锋,许江文.基于粗糙集与遗传算法的储层识别技术.断块油气田,2014,21(2):196–200.

11薛兴思.基于遗传算法的本体映射技术.福建工程学院学报,2014,12(1):74–77.

12高尚,杨静宇,吴小俊,等.圆排列问题的蚁群模拟退火算法.系统工程理论与实践,2004,8 (8):102–106.

13章义刚,王会颖.改进蚁群算法求解圆排列问题.机电工程,2008,25(5):92–95.

14刘晓霞,窦明鑫.一种改进的自适应遗传算法.合作经济与科技,2012,(5):127–128.

15张愉,娄卉芳,文良浩,等.一种改进的遗传算法交叉策略.湖南科技大学学报(自然科学版),2012,27(1):94–97.

Solving Circle Permutation Problem Using Improved Genetic Algorithm

XU Xiao-Ping1,ZHU Qiu-Qiu1,TAI Hui-Qiang2
1(School of Sciences,Xi’an University of Technology,Xi’an 710048,China)
2(School of Mechanical and Precision Instrument Engineering,Xi’an University of Technology,Xi’an 710048,China)

Abstract:Circle permutation problem is a typical combinatorial optimization problem; moreover,it is a NP complete problem.Genetic algorithm is a kind of evolutionary method based on natural biological evolution.It is simple and easy,and has characteristics of abstraction and robustness.which has been successfully applied to many engineering optimization problems.A new method based on improved genetic algorithm is presented for solving circle permutation problem.Firstly,the relationship between circular permutation problem and the traveling salesman problem is analyzed,and then circular permutation problem is translated into traveling salesman problem.Next,it is solved by the improved genetic algorithm.Finally,in the simulation experiments,compared with the existing algorithm,the proposed method is a simple and effective algorithm for solving circle permutation problem.

Key words:circle permutation problem; combinatorial optimization; genetic algorithm; evolutionary algorithm

基金项目:①国家自然科学基金(61273127);陕西省自然科学基础研究计划(2014JM8325);陕西省教育厅科研计划(14JK1538)

收稿时间:2015-07-06;收到修改稿时间:2015-09-28