错误的“水土压力统一计算理论”和“考虑土对水吸附性的渗流破坏理论”
——与王洪新先生商榷《考虑土对水吸附性的渗流破坏理论与应用》一文
2016-06-17方玉树后勤工程学院重庆400041
方玉树(后勤工程学院,重庆 400041)
错误的“水土压力统一计算理论”和“考虑土对水吸附性的渗流破坏理论”
——与王洪新先生商榷《考虑土对水吸附性的渗流破坏理论与应用》一文
方玉树
(后勤工程学院,重庆400041)
摘要:王洪新在《岩石力学与工程学报》2013年5期发表的《考虑土对水吸附性的渗流破坏理论与应用》一文,着重研究考虑土对水吸附性的渗流破坏和基坑突涌稳定性计算以及作为这些计算基础的水压率、浮力、浮重度、渗透力等议题,也据此对他本人先前关于水土压力统一计算的论述进行了修正。结合水压率理论对该文发表不同看法。
关键词:水压率;浮重度;渗透力;水力坡度;挡墙侧压力;基坑突涌稳定性
王洪新先生在《岩石力学与工程学报》2013年5期发表的《考虑土对水吸附性的渗流破坏理论与应用》一文,着重研究考虑土对水吸附性的渗流破坏和基坑突涌稳定性计算以及作为这些计算基础的水压率、浮力、浮重度、渗透力等议题(他将这些论述称为“考虑土对水吸附性的渗流破坏理论”),也据此对他本人先前关于水土压力统一计算的论述(他将其称为“水土压力统一计算理论”)【1,2】进行了修正。笔者在2007年发表的水压率理论【3】对这些议题均已有研究,现结合水压率理论对该文发表不同看法。
1 水压率的理解、计算和用词
1.1水压率的理解
水压率理论【3】在孔隙水压力是单位面积土截面上的水压力、孔隙水压力(及总应力和有效应力)所涉及的截面是在颗粒(或胶团)之间通过的宏观上是平面的曲面、结合水不传递水压力这三个基础上,提出下列孔隙水压力表达式(称水压原理)并将有效应力原理建立在水压原理这个基础上:

式中u-孔隙水压力,γw-水重度,h-压力水头,ξ-水压率,为土截面上的自由水面积率,即孔隙水压力与水体中的水压应力(即水体水压强)的比率。
根据王先生给出的挡墙侧压力计算公式【即本文(30)和(31)式】中的水压力项ξsγwh可知,王先生事实上接受并引用了水压率理论给出的(1)式,只是将水压率改称为产生浮力截面上自由水所占面积与截面总面积之比或土中水的压力系数,并将其符号改为ξs。
但王先生认为水压率理论中的水压率属于体积比性质,这是对水压率理论的误解。水压率理论将水压率明确定义为土截面上的自由水面积率,即孔隙水压力与水体中的水压应力(即水体水压强)的比率。因此,水压率属于面积比性质而不是体积比性质。其实,因水压是面力,“水压率”一词本身就说明它属于面积比性质。笔者只是曾提出用自由水体积与孔隙体积之比这个体积比(也即用给水度与孔隙度之比)来估计土体内部的水压率而已。鉴于按这种方法估计的水压率在理论和实作上都偏小,笔者现已放弃这种方法而提出采用特殊形状土体抗浮试验和水荷载作用下的单向压缩试验测定土体内水压率的方法【4】。
1.2水压率的计算
王先生新给出了ξs与初始水力坡度ib的如下关系式(王先生称其为理论关系式):

此外,王先生还认为“梅国雄等所做的浮力实验(注:指土上物体浮力试验)得到的土中浮力与阿基米德定律计算的浮力之比可以看作ξs,但浮力试验由于浮体存在侧摩阻力容易出现较大误差”。按王先生的意思,如果克服了浮体的侧摩阻力(将物体无埋深地置于土体表面就能做到这一点),ξs就能根据土上物体浮力试验确定,也就是说,土体与物体接触面的ξs就是土体内部的ξs。
王先生的这些做法和认识都是不正确的。
1.水头差由渗流中的阻力引起,没有渗流就没有水头差也就没有水力坡度,故初始水力坡度是不存在的;另外,达西定律不含初始水力坡度,故接受初始水力坡度这个概念还会造成达西定律和相应渗透系数定义与数据对细粒土的失效【3,5,6】,因此,(2)式是错误的。
2.土体内部水压率和土体与其它物体接触面水压率是不同的。当接触面非胶结面时,土体与其它物体接触面水压率一般大于土体内部水压率,土的稠度越大,两者差别越大。物体置于坚硬致密土体上时,虽然土体内部的水压率几乎为0,但土体与物体接触面因是不连续面(间断面),其水压率则远远大于0。对无胶结和结晶联结的有粘性土而言,土体内外水压率的差异类似于土体内外粘性的差异,但数值大小关系相反。当接触面为胶结面(如在土体表面现浇的混凝土构件与土体的接触面)时,其水压率可取与土体内部水压率【3,5,6】,因此,土上物体浮力试验得到的水压率是土体与物体接触面的水压率而不是土体内部的水压率。
1.3水压率的用词
水压率理论中的“水压率”过去就被王先生改称为“孔隙水压力折减系数”、“能够产生孔隙水压力的比率”、“能够产生孔隙水压力的比率系数”、“土水共同作用系数”、“土水共同作用压力系数”、“浮力折减系数”【1,2】,如今又被其改称为“产生浮力截面上自由水所占面积与截面总面积之比”或“土中水的压力系数”。如此频繁变换水压率称谓的做法是极不严肃的。当有研究者在文章中首次使用某个术语表达某个概念时,后来的研究者应继续使用这个术语,除非使用一个新的术语更加恰当。当认为使用一个新的术语更加恰当时,也应说明情况。王先生不仅未说明情况,就连这些称谓就是水压率、是水压率的替换称谓这一点也未告知,这种刻意回避水压率称谓的做法是错误的。
考虑到水压率这个参量反映的是单位土截面上的水压力(即孔隙水压力)占单位水截面上的水压力(即水体水压强)的比例(即两种水压之比率),且这个参量是一个新的水理性质指标【3】,将这个参量称为水压率是恰当的。
替换水压率的上述8个称谓并不比“水压率”更恰当,这是因为:1.“能够产生孔隙水压力的比率系数”语法有误、语义不明;2.“土中水的压力系数”、“土水共同作用系数”与“土水共同作用压力系数”中,“系数”一词本身不一定是“比率”(如渗透系数、摩擦系数);3.“土中水的压力系数”一词也可以理解为水压率与水重度的乘积;4.“土水共同作用系数”与“土水共同作用压力系数”中作用和压力类型不明(未表明是水压力);5.“土水共同作用压力系数”将“作用”与“压力”组合在一起不恰当(压力本身就是作用);6.“浮力折减系数”和“产生浮力截面上自由水所占面积与截面总面积之比”混淆了浮力与孔隙水压力两个概念;7.“孔隙水压力折减系数”未反映孔隙水压力与水体水压强相等的情形。因而这8个用词都没有清楚地反映孔隙水压力与水体水压强这两种水压之比率。此外,这8个称谓均相对不够简洁,均不适用于一个新的水理性质指标的命名。因此,用王先生的这8个词替换水压率是多余的,也不利于理解。
2 浮力的计算
对顶面不低于水位面的结构物和以地面为顶面且地面不低于水位面的土体,水压率理论给出的结构物和土体所受浮力F公式为【3】:

式中,V为结构物水下部分体积。
王先生给出的土中结构物所受浮力公式除了将水压率ξ换为土中水的压力系数ξs外,其余与上相同。由于土中水的压力系数ξs就是水压率理论中的水压率ξ,故王先生的土中结构物所受浮力公式事实上引自水压率理论,但王先生没有给出浮力公式适用范围,这意味着在王先生看来水压率理论给出的(3)式对所有情形都适用。此外,王先生给出的浮力公式虽是针对结构物的,但王先生在计算胶团(颗粒与结合水的组合体)所受浮力时也用该公式,这意味着在王先生看来水压率理论给出的(3)式也适用于土体和土体中的微单元。
王先生的这些做法和认识是错误的:
1.(3)式对与地下水连通且水位与之相同的地表水位面下方的结构物和土体不适用。对这种情形,根据结构物或土体底面与顶面水压差可得如下浮力计算公式【3】:
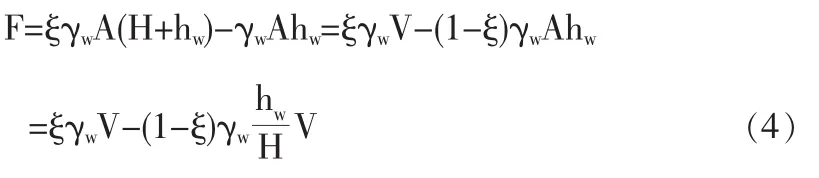
式中A为结构物或土体底面积,hw为结构物或土体顶面处压力水头(即水深),H为结构物或土体高度,ξ为结构物底面(即结构物与土体接触面)或土体底面水压率。由此可知,当结构物底面总水压因水压率很小而小于顶面总水压或土体底面总水压因水压率很小而小于地面总水压时,浮力方向朝下。
2.(3)式作为土体中微单元浮力计算方法对多层土体不适用。
由(4)式可得单位体积浮力计算公式:

从上式可知,当水位面高于地表且土的水压率不等于1时,土体所受单位体积浮力计算范围向上需到达地面,向下需到达土体底面,计算所用水压率是土体底面的水压率。
将(3)式用于土体所受浮力计算时,因式中水压率是土体底面水压率,故由(3)式计算该土体内部微单元所受浮力时水压率也应取该土体底面水压率而不是取该土体内部微单元所在截面水压率。
对多层土体,各层土水压率不同,故土体底面水压率不同于该土体内部微单元所在截面水压率。王先生在计算土体中胶团所受浮力时不要求水压率取土体底面水压率,显然这种做法对多层土体不适用。
3.如本文1.1节所指出的那样,土体与结构物接触面的水压率与土体内部水压率是不同的。
3 浮重度的计算
3.1王先生浮重度计算方法的分析
王先生给出的浮重度γ'计算式为:

式中,γsat为饱和重度;ξ0为土水共同作用系数(注:原文符号为ξ,为与水压率理论中的水压率符号ξ区分开来,改用ξ0),其定义式为:

式中,ξv为自由水所占体积与孔隙总体积之比,e为孔隙比。
ξ0由(7)式定义的(6)式是错误的,这是因为用浮重度计算土的有效自重应力应与用有效应力原理计算土的有效自重应力等效。详细说明如下:
根据(1)式和有效应力原理

由多个水平土层组成的土体中某点的竖向有效自重应力σ'cz应按下式计算:

式中m1、m2分别为计算点以上土层中水位面以上和以下土层数,γi、γj分别为水位面以上第i层土和水位面以下第j层土的重度,hi、hj分别为水位面以上第i层土和水位面以下第j层土的厚度,ξm2为第m2层土的水压率(分层界面处取较大值)。
上式可改写为

据此,计算点以上水位面以下任意一层土的浮重度为【1】

从(9)式至(11)式可得以下认识:
1.浮重度算法(指用浮重度计算土的有效自重应力的方法)与有效应力原理算法(指用有效应力原理计算土的有效自重应力的方法)中涉及的水压率相同,也就是说,王先生中的土水共同作用系数ξ0和土中水的压力系数ξs是同一个参数,都是水压率理论中的水压率。其实,(6)式与(3)式也是矛盾的。在(6)式中ξ0γw是单位体积土所受浮力,按照(3)式,(6)式中的ξ0就是ξs。
2.某层土的浮重度计算中所涉及的水压率不是该层土的水压率而是有效自重应力计算点所在土层的水压率,(6)式中土水共同作用系数ξ0替换为水压率后,(6)式对多层土仍不适用。
上述情况表明,(6)式中土水共同作用系数ξo替换为水压率后,(6)式是水压率理论已经给出的(11)式的特例。
3.2浮重度计算方法错误带来的问题
王先生浮重度计算方法的上述错误必然造成用浮重度计算有效自重应力、含有效自重应力的有效应力、挡墙土压力、渗流破坏稳定性和基坑突涌稳定性的混乱和错误。
以基坑突涌为例,王先生根据错误的(6)式得到如下错误的临界方程:

式中,ξs1,ξs2分别为承压含水层及其顶板土中水的压力系数,ξ01为承压含水层顶板土水共同作用系数,γsat为承压含水层顶板饱和重度,H为基坑底到承压含水层顶面的距离。王先生据此得出“上覆土层有一定透水性时,上覆土层厚度要求比传统算法计算的大,此时传统算法是偏于不安全的”这一错误结论。
事实上,当上覆土层有一定透水性时,在基坑下挖的过程中,承压水头随着水的渗出而降低,临界厚度随之减小。基坑下挖到原临界厚度时,因临界厚度减小,基坑突涌还未到临界状态。这就是说,当上覆土层有一定透水性时,上覆土层厚度要求比传统算法计算的小,此时传统算法是偏于安全的。当承压含水层水压率不等于1时更是如此。
根据(1)式和有效应力原理可写出下列基坑突涌临界方程:

由此笔者早在2007年就得到下列基坑突涌临界厚度计算式【1】:

因承压系统属于多层土体,承压含水层与隔水顶板、底板的水压率差别很大,而饱和重度差别不大,故承压含水层顶面处土体重与总孔压差别最小。因此,基坑突涌临界方程应建立在此处,若发生基坑突涌,此处就是基坑突涌发生的源头。当上覆土层为不透水的黏土层时,王先生“承压水层含有一定细粒成分时,上覆土层厚度要求比传统算法小”的结论是(14)式的必然结果,并不需要通过(12)式得到。
3.3王先生浮重度计算公式推导过程的分析
王先生之所以得出ξ0由(7)式定义的(6)式,是因为推导过程存在错误。王先生通过胶团重与胶团所受浮力之差计算土的浮重,不计自由水的浮重(即将孔隙中自由水的浮重取0),同时胶团所受浮力按(3)式计算。这种推导过程存在三个问题:
1.根据本文第2部分分析结果,(3)式对与地下水连通且水位与之相同的地表水位面下方的结构物和土体不适用,故胶团所受浮力按(3)式计算的做法对与地下水连通且水位与之相同的地表水位面下方的结构物和土体不适用。
2.根据本文第2部分分析结果,计算胶团所受浮力时所用ξs应是计算浮重之土体底面的ξs而不是胶团所在截面的ξs,故采用胶团所在位置ξs计算胶团所受浮力的做法不适用于多层土。
3.当ξs不等于1时,用胶团浮重代表土体浮重是错误的。土体浮重是胶团浮重与胶团间自由水浮重之和。自由水体积为ξve△Vs,自由水重为ξvγwe△Vs,自由水所受浮力为ξsξvγwe△Vs(△Vs为土单元颗粒体积),故自由水浮重为(1-ξs)ξvγwe△Vs。把自由水浮重计入土的浮重后,所得浮重度中土水共同作用系数ξ0便与土中水的压力系数ξs相等。
顺便指出,王先生在浮重度推导中用到的ξsγw[1+(1-ξv)e]△Vs是胶团所受浮力,王先生将其称作“土颗粒(体积为△Vs)受到的浮力”是错误的。
从这里可以看出,通过分析土中各个组分的浮重来推导土的浮重度不仅繁琐而且容易出现差错,直接用(1)式和有效应力原理来推导则很简单;对多层土,因浮重度计算公式中的水压率随有效自重应力计算点所在土层的不同而不同,用浮重度计算有效自重应力不仅不能简化计算过程而且容易出现差错,直接用(1)式和有效应力原理来计算则比较简单。这正是水压率理论【3】已经得出的结论。
4 渗流破坏临界方程
土体浮动临界状态满足下列方程:

式中,σ为土体底面总应力,u为土体底面孔隙水压力。
当渗流方向垂直向上、水位高于地面时,对以地面为顶面的直立土柱,土柱底面总应力为:


式中h为土柱底面压力水头,ξn为土柱底面水压率(在分层界面取较大值)。因此,(15)式可写成

上式可写成:

因h-(hw+H)为土柱底面与顶面水头差△z=z2-z1【z1,z2为土柱顶面(即地面)、底面水头高度】,故上式可写成:

式中I为水力坡度。由此,(20)式可写成

上式右边随土体底面水压率ξn的减小而减小。由此式可得下列临界水力坡度计算式:

笔者曾给出下列临界水力坡度计算式【3】:

显然上式只适用于无地表水的情形。当ξn=1时,(23)式成为

因土的饱和重度相对变化范围小于水压率变化范围,故由(23)式知,多层土柱的底面应取在水压率最大土层的顶面。
根据(23)式可以分析为何有时水力坡度远大于1时没有发生流土,也可以分析为何有时水力坡度远小于1时发生了潜蚀。对潜蚀而言,式中饱和重度应是粗粒间由细粒和水构成的土管的饱和重度,它随土管内细粒土密实度变化,土管内只有几个细粒时,土管饱和重度接近于自由水重度。
王先生针对多层土中任意土层给出如下渗流破坏极限平衡方程【为避免与(20)式中角标数字混淆,用i和i+1替换原文中的1和2;为避免与压力水头混淆,用z替换原文中的h】:
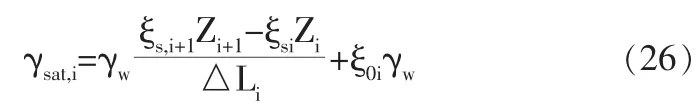
式中,ξsi,ξs,i+1为第i土层顶面、底面土中水的压力系数,ξ0i为第i土层顶面土水共同作用系数,△Li为第i土层高度,zi,zi+1为第i土层顶面、底面水头高度。
王先生的做法存在下列问题:
1.未将式中ξ0i取与ξsi相同的值。
2.既不要求选择水压率最大土层的顶面做土柱的底面,也不要求以地面为土柱的顶面,导致方程失效:在水压率最大土层顶面做底面、地面做顶面的土柱中,因受其它层影响,某层满足(26)式不代表土柱要发生渗流破坏,某层不满足(26)式(等号左边大于右边)也不代表土柱不发生渗流破坏。因而,ξ0i取与ξsi相同的值后,(26)式仍是错误的。
5 渗透力和水力坡度的计算
5.1渗透力的计算
王先生针对多层土中任意土层给出如下单位体积渗透力Di表达式【为避免与(20)式中角标数字混淆,用i和i+1替换原文中的1和2;为避免与压力水头混淆,用z替换原文中的h】:

式中各符号意义同前。
王先生还将土对水无吸附性时式中γwZi,γwZi+1解释为第i土层顶面和底面受到的土中水压力。
这些做法存在下列问题:
1.式中的水头是总水头而不是压力水头,土对水无吸附性时,式中γwz1,γwz2显然不是土单元顶面和底面受到的土中水压力。
2.根据(5)式,(20)式中ξnγw-(1-ξn)γwhw/H为单位体积土体所受浮力,因此,(20)式中涉及水头差项ξnγw(z2-z1)/H就是单位体积土体所受渗透力,即有

从(5)式可知,当有与地下水连通的地表水且土的水压率不等于1时,土体所受浮力计算范围向上需到达地面,向下需到达土体底面,计算所用水压率是土体底面的水压率。在渗流条件下渗透力和浮力相伴而生,针对同一个对象,故土体所受渗透力计算范围和水压率取值应与此相同。(27)式的计算范围向上未到达地面,向下未到达土体底面,计算所用水压率也不是土体底面的水压率,因而是错误的。
5.2水力坡度表达式
王先生将考虑土对水吸附性后的水力坡度I表达式改为:

式中,z1,z2为土单元顶面、底面水头高度(原文符号为h1,h2,为与相应压力水头清楚地区分开来,改用z1,z2)。
此式存在下列问题:
1.根据达西定律,渗透速度是渗透系数与水力坡度的乘积,其中水力坡度是沿流线的水头损失率,与水压率无关,采用(29)式将造成达西定律失效。
2.水力坡度涉及的水头是总水头,是位置水头和压力水头之和,而水压率是用于计算孔隙水压力的,是与自由水重度、压力水头相伴的,总水头与水压率的乘积没有物理意义。
因此,(29)式是错误的。
由本文第4部分可知,渗流破坏稳定性计算是力平衡问题,水力坡度概念对此可有可无。但若采用了水力坡度概念,水力坡度就应是从土柱底面到地面范围的水力坡度(对多层土,以水压率最大土层顶面做土柱底面)。
真正需要应用水力坡度概念的是渗流计算和与渗流有关的固结计算。在这些计算中,常常要用到土体中某点的水力坡度,此时水力坡度表达式是微分式。因此,水力坡度概念是必要的而且可以采用微分式表达。
6 挡墙侧压力的计算
王先生给出的挡墙侧压力计算公式为:

式中,h为从地面起算的计算点深度;c和φ为“统一强度指标”概念下的粘聚力和内摩擦角,按下式计算:

王先生的这套公式存在多方面错误:
1.竖向有效自重应力计算错误。根据(6)式知,式中竖向有效自重应力是用王先生给出的浮重度计算的,如第3部分所述,王先生的浮重度计算是错误的,故竖向有效自重应力计算是错误的。
2.“统一强度指标”概念错误。王先生的“统一强度指标”是将有效应力强度指标和不排水总应力强度指标组合起来使取值可在这两类指标之间过渡的强度指标,这个概念是错误的。有效应力强度指标对应于剪切面上的法向有效应力,总应力强度指标对应于剪切面上的法向总应力。剪切面上的法向应力采用有效应力时应采用有效应力强度指标,剪切面上的法向应力采用总应力时应采用总应力强度指标。原则上抗剪强度均应采用有效应力和有效应力强度指标进行表达,考虑到有效应力强度指标相对不易获取,工程实用上允许根据排水条件选用不同总应力强度指标进行表达。“统一强度指标”既不是有效应力强度指标也不是总应力强度指标,既不对应于剪切面上的法向有效应力,也不对应于剪切面上的法向总应力,是没有意义的。挡墙水土压力采用分算方法时,因其中土压力强度本身及土压力强度计算所用竖向自重应力均是有效应力,故土压力强度计算所用抗剪强度指标应是有效应力强度指标。王先生将“统一强度指标”用于这种计算是错误的。根据有效应力原理,有效应力强度指标就是唯一的强度指标。
其实,饱和粘性土各类强度(及其指标)同水压率一样也是随稠度的变化而变化的,这些强度(及其指标)本身会随着稠度的增大而趋同。
饱和粘性土轴对称固结不排水三轴试验中孔隙水压力这个超孔隙水压力△u与大小主应力增量差(△σ1-△σ3)的关系式为(式中A为孔隙压力系数):

众所周知,孔隙压力系数A随粘性土稠度的增加而降低。根据(34)式,随着孔压系数A减小直至0,超孔隙水压力减小直至0,有效应力增大直至总应力,此时,有效应力强度(及其指标)与固结不排水强度(及其指标)、固结排水强度(及其指标)趋于相等。同时,当稠度很大时,土的变形模量很大,土的固结变形量很小,因而固结不排水强度(及其指标)与不固结不排水强度(及其指标)也趋于相等。当饱和土不含自由水(如坚硬致密粘土)时,因土不再渗透固结,有效应力强度(及其指标)与固结不排水强度(及其指标)、不固结不排水强度(及其指标)、固结排水强度(及其指标)相同。这正是水压率理论【3】认为“当水压率很小时……有效应力强度指标接近于总应力强度指标,有效土压力系数接近于总土压力系数”的原因。
3.上述公式的推导过程中孔隙水压力和有效应力概念不清。
(1)根据(30)和(31)式中的水压力项可知,王先生事实上接受了(1)式并用该式计算孔隙水压力,但王先生又采用如下有效应力原理表达式并将式中u称为孔隙水压力:

这就导致u和ξu两个孔隙水压力。在孔隙水压力概念不清的情况下,由(35)式表达的有效应力原理无法在文字上进行阐述。
早在王先生引用(35)式之前,李广信先生就指出(35)式违反了有效应力原理【7】。王先生在引用李先生文章中出现的(35)式之时对此置之不理,这种做法是不正确的。
(2)众所周知,固结不排水三轴试验中所测孔隙水压力是超孔隙水压力(在单向固结试验中超孔隙水压力的最大值就是所施加的荷载)。其值本身就应是王先生已接受并已引用的(1)式中的u也即(35)式中的ξu。王先生却在推导(32)和(33)式的过程中将所测孔隙水压力视为水体水压强γwh也即(35)式中的u(即不包含ξ),按照这种认识,若仍按(1)式计算孔隙水压力,就会造成单向固结试验中加载瞬间引起的超孔隙水压力大于荷载本身,有效应力为负,土体回弹这种荒谬结果。徐日庆先生等人就曾这样得到一维固结也可以有Mandel-Cryer效应的错误结论【8,9】。
令人不解的是,王先生本人已经在2012年的文章中否定了他在2011年文章中提出的(32)和(33)式并重新给出公式(自然地,由于“统一强度指标”概念本身错误,重新给出的“统一强度指标”公式也是错误和无意义的),如今王先生又在不加任何说明的情况下将其重新颠倒过来,这样做是极不严肃的。
此外,(30)和(31)式等号右边前两项未含h,并且在给出这两个公式时未列出墙背直立光滑、土体均质、表面水平且无附加荷载、地下水位面与土体表面平齐等条件。
上述情况表明,导出(30)-(33)式远非王先生所说“建立起在逻辑上极为严谨的水土压力统一计算理论”,恰恰相反,导出和恢复使用(30)-(33)式的过程完全无逻辑可言。
7 其它
7.1基坑突涌稳定性计算的理解
王先生将基坑突涌稳定性计算视为“上覆土层采用水土合算,承压水层采用水土分算”。这是错误的。
1.水土分算和合算是当前挡墙侧压力计算的两种算法,不涉及竖向压力计算。在目前的挡墙侧压力计算中,由于分算和合算所用的侧向土水压力系数及强度指标不同,水土分算和合算结果是不同的。但在竖向上,无论水土分算还是水土合算,因不涉及侧向土水压力系数及强度指标,上覆土重都是相同的。由于结果相同,就无所谓水土分算和合算。
2.水土分算并不是只算其中的土压力或只算其中的水压力,而是水压力和土压力分别计算后再相加。基坑突涌稳定性计算时,对承压含水层只需要计算承压水在隔水顶板底面产生的压力。这种计算显然不是水土分算。
7.2浮力、浮重度、渗透力和水力坡度用词
王先生将考虑结合水影响后的浮力、浮重度、渗透力和水力坡度分别称为广义浮力、广义浮重度、广义渗透力和广义水力坡度。这是错误的。广义是相对于狭义而言一个概念的适用范围更宽的意思。考虑结合水影响后,浮力、浮重度、渗透力和水力坡度这些概念(而不是计算方法)的适用范围没有在既有适用范围基础上扩展,怎能冠以广义一词呢?
8 结语
1.根据王先生给出的挡墙侧压力计算公式中的水压力项ξsγwh可知,王先生事实上接受并引用了水压率理论提出的孔隙水压力表达式(称水压原理)即(1)式;王先生给出的浮力公式即(3)式是水压率理论给出的若干浮力公式中的一个。
2.与水压率理论进行对比可知,“水土压力统一计算理论”和“考虑土对水吸附性的渗流破坏理论”不同于水压率理论之处是:
(1)回避和频繁变换水压率理论中的水压率称谓;
(2)给出水压率与初始水力坡度的关系式即(2)式;
(3)不区分土体与物体接触面的水压率与土体内部的水压率;
(4)计算物体和土单元浮力时只引用水压率理论的两个浮力公式中较简单的那一个即(3)式;
(5)给出不同的浮重度计算式即(6)式;
(6)根据不同的浮重度计算式给出不同的基坑突涌临界方程即(12)式;
(7)根据不同的浮重度计算式给出不同的渗流破坏极限平衡方程即(26)式;
(8)给出不同的单位体积渗透力表达式即(27)式和水力坡度表达式即(29)式;
(9)提出不同的粘聚力和内摩擦角计算式即(32)和(33)式(称“统一强度指标”计算式);
(10)引用不同的有效应力原理表达式即(35)式;
(11)根据“统一强度指标”计算式和不同的浮重度计算式给出不同的挡墙侧压力计算公式即(30)和(31)式;
(12)将考虑土对水吸附性后的浮力、浮重度、渗透力和水力坡度分别称为广义浮力、广义浮重度、广义渗透力和广义水力坡度。
逐一分析的结果表明,这些做法都是错误的。其中,水压率公式因初始水力坡度不存在而错误,浮重度计算式(6)式因相应有效自重应力与用有效应力原理计算所得不等效而错误,有效应力原理表达式(35)式和“统一强度指标”计算式(32)、(33)式因孔隙水压力概念混乱而错误,水力坡度表达式(29)式因水头概念错误而错误,基坑突涌临界方程(12)式因浮重度计算式错误而错误,渗流破坏极限平衡方程(26)式因浮重度计算式错误且既不要求选择水压率最大土层的顶面做土柱的底面也不要求以地面为土柱的顶面而错误,单位体积渗透力表达式(27)式因所在渗流破坏极限平衡方程和浮力计算错误而错误,挡墙侧压力计算公式(30)和(31)式因“统一强度指标”概念和浮重度计算错误而错误。因此,“水土压力统一计算理论”和“考虑土对水吸附性的渗流破坏理论”是完全错误的。
3.本人曾经详细分析了徐日庆先生等人的“两相非连续介质固结理论”的错误【9】。综观“水土压力统一计算理论”、“考虑土对水吸附性的渗流破坏理论”和“两相非连续介质固结理论”,虽然它们的错误不尽相同,但都有一个根本性错误,就是孔隙水压力概念含混不清:有时将按水体水压强计算的值视为孔隙水压力,有时又将它与某个系数的乘积视为孔隙水压力,或者同时将二者视为孔隙水压力。这表明水压率理论中以本文(1)式表达的水压原理是极其重要的,研究与孔隙水压力有关的问题须从水压原理出发而不是从有效应力原理开始。
4.本文以及笔者此前发表的文章【4-6】表明,早在2007年就发表的水压率理论【3】已经涵盖了“水土压力统一计算理论”和“考虑土对水吸附性的渗流破坏理论”以及“两相非连续介质固结理论”所涉及的范围,已经从理论上解决了王洪新先生和徐日庆先生等人共同或分别关注的细粒土浮力折减、水土压力的分算和合算、考虑土对水吸附性的渗流破坏和基坑突涌稳定性计算、细粒土固结等问题以及其它与孔隙水压力有关的问题。
参考文献:
[1]王洪新.水土压力分算与合算的统一算法[J].岩石力学与工程学报,2011,30(5):1057-1064.
[2]王洪新.水土压力统一计算理论的证明及水土共同作用下的压力计算[J].岩石力学与工程学报,2012,31(2):392-398.
[3]方玉树.基于水压率讨论土中孔隙水压力及有关问题[J].岩土工程界,2007,10(5):21-26.
[4]方玉树.关于水压率理论与有效应力原理的几个问题[J].重庆建筑,2016,15(3):55-58.
[5]方玉树.水压率理论被推翻了吗[J].岩土工程界,2007,10(11):21-26.
[6]方玉树.水压率理论释疑[J].岩土工程界,2008,11(4):21-26.
[7]李广信.再议水压率[J].岩土工程界,2008,11(2):21-24.
[8]徐日庆,等.两相非连续介质固结理论[J].岩石力学与工程学报,2014,33(4):817-825.
[9]方玉树.错误的“两相非连续介质固结理论”——与徐日庆先生等商榷“两相非连续介质固结理论”一文[J].重庆建筑,2016,15(2):55-56.
责任编辑:孙苏,李红
The Fault "Unified Calculation Theory on Water-Soil Pressure" and "Seepage Failure Theory Considering Water-Soil Absorptivity"
Keywords:water pressure;submerged unit weight;seepage force;hydraulic gradient;lateral pressure of retaining wall;up-bursting stability of pit foundation
Abstract:Wang Hongxin published his paper Seepage Failure Theory and its Application Considering Water-Soil Absorptivity on Chinese Journal of Rock Mechanics and Engineering in no.5,2015,studying seepage failure considering water-soil absorptivity and the up-bursting stability calculation of pit foundation as well as the calculation bases like water pressure rate,buoyance,submerged unit weight and seepage force etc.,with his prior illustration amended.The author presents some different views on the paper based on water pressure theory.
中图分类号:TU43
文献标识码:A
文章编号:1671-9107(2016)04-0053-07
doi:10.3969/j.issn.1671-9107.2016.04.053
收稿日期:2016-02-04
作者简介:方玉树(1958-),男,江西婺源人,硕士,教授,国家注册土木工程师(岩土),主要从事与岩土体稳定有关的研究和勘察设计工作。
