一种新的粒子群优化聚类算法

张俊溪，杨海粟（.西安航空学院车辆工程系，西安　70077；.西安电子工程研究所，西安　7000）



一种新的粒子群优化聚类算法

张俊溪1，杨海粟2
（1.西安航空学院车辆工程系，西安710077；2.西安电子工程研究所，西安710100）

摘 要：K-means算法在聚类分析中有着广泛应用。它采用了均值中心这一启发式信息，具有计算效率高的优点，但对初始聚类中心选择敏感，且容易陷入局部最优。PSO算法的随机性和并行性特点使其在处理数据库形式的海量数据中表现出更大的优越性，不仅具有较强的全局搜索能力，同时，通过对PSO算法搜索过程的改进增强了算法在最优解附近的搜索概率，降低样本对初始化敏感的程度，可以弥补K-means算法的缺陷。将改进的PSO算法应用于K-means聚类算法可以提高算法的稳定性和收敛效率，通过四组标准UCI数据集的试验，验证了新算法的有效性。

关键词：K-平均算法；粒子群优化算法；聚类中心；稳定性；搜索；收敛；敏感

1 引 言

聚类分析是数据挖掘的一个重要分支，是一种重要的非监督学习方法。聚类是按照事物空间、时间或属性等特点将其划分成多个类别的过程，并要求类间的相似性最小，类内的相似性最大［1］。目前聚类分析的方法较多，根据不同聚类方法将其划分为7种类别：基于划分的聚类、基于层次的聚类、基于密度的聚类、基于网格的聚类、基于模型的聚类、字符属性联合聚类和神经网络聚类等［2］。其中基于划分聚类中的K-means算法是应用最为广泛的算法，该算法以样本中任意位置为初始中心，以样本到聚类中心的平均距离之和作为适应度函数，具有模型简单、计算效率高的优点。但由于K-means算法基于适应度函数极值的方法来优化目标函数，存在易于陷入局部最优和处理海量数据效率低等缺点。近年来对该算法的改进是聚类领域的研究热点，出现了将遗传算法、PSO算法、人工免疫算法、蚂

❋蚁算法及其相关改进算法与k-means相结合的多聚类算法等。

粒子群算法通过模拟自然界鸟群或鱼群等生物的觅食行为，将其觅食过程中的学习和经验作为更新手段，来达到最优目标的模式，具有随机性和并行性的特点，全局搜索能力强，适合于处理数据库形式的海量数据，与聚类算法相比不易陷入局部最优。但是鉴于基本粒子群优化算法在搜索空间中对解搜索的盲目性和对最优解空间搜索缺乏针对性，近年来提出了大量的改进算法。常见粒子群改进的优化算法有：带惯性权重的标准粒子群算法，通过给粒子群的速度公式乘以惯性权重因子来改变粒子的速度［3］；将免疫算法中的免疫信息处理机制引入到粒子群算法中的免疫粒子群算法［4］；将混沌理论中混沌运动的遍历性引入到粒子群搜索过程中，将粒子群搜索的最优位置与混沌序列的最优位置粒子进行比较获得最优解的混沌粒子群算法［5］；将协同理论引入到粒子群算法中，通过将位置向量加入到粒子群的适应度函数计算适应度值，提高算法的收敛精度［6］。

通过去掉随机粒子群算法模型中的当前速度，使速度本身失去记忆性，同时在搜索空间中重新随机产生新的微粒取代原始微粒，可以大大增强全局搜索能力。将耗散结构的自组织性加入到粒子群算法，粒子在搜索过程中的更新不仅依赖历史经历，还要受环境影响，通过附加信息使得系统处于不平衡状态，从而使群体进化能力增强［7］。无论是哪一种改进方法，目标都是为了提高PSO算法收敛的速度和收敛解的精度。本文基于此提出了一种对适应度值权重分配的PSO算法，并将其应用于K-means聚类算法中，通过两组人工数据和两组UCI数据，试验结果表明改进的PSO应用于K-means算法与基本PSO算法相比具有较快的收敛速度和较好的收敛解。

2 k-means聚类算法基本原理

K-means算法的实现过程是，指定聚类的数目k，随机产生k个聚类中心，将待聚类对象分给最近的簇中心，依据最近邻法则［8］进行赋值，通过计算每个簇中个体与聚类中心的距离平均值，并更新为新的聚类中心［9］，反复迭代直至误差准则函数达到最小值，如公式（1）所示：

其中p为空间的点，即数据对象，mi是簇Ci的聚类中心。E值越小表示类内数据越相似。经典的K-means算法过程描述如下［1］：

输入：簇的数目k和包含n个对象的数据库；

输出：平方误差总和最小条件下的k个簇；

①指定聚类数目K，随机选择其初始聚类中心；

②根据最近邻法则将所有对象划分到相应的簇中；

③根据误差准则函数E计算适应度值，并更新每个簇中心；

④若未达到结束条件，则转②重复；

⑤输出结果。

3 粒子群优化算法及其改进

PSO大规模应用于聚类算法始于2002年，Omran等人［10］在对PSO算法进行大量分析研究后，提出了一种基于粒子群优化的无指导图像分类算法。

在基于粒子群算法的聚类分析中，每个粒子代表K个类的中心点，这样每个粒子就包含一个表示簇中心的数据向量，整个粒子群则代表了对数据的多种划分。基本PSO算法的适应度函数为Je，如公式（2）所示：

其中，

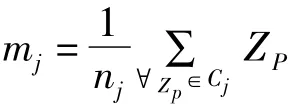
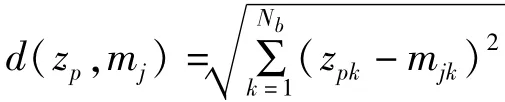
基本PSO算法流程如下：

（1）初始化粒子群并根据适应度函数计算各粒子的适应度值；

（2）寻找历史最优解，将每个粒子的适应度值与它的历史最优适应度值比较，取二者之中较优的一个；

（3）寻找最优位置适应度值，将每个粒子的适应度值和群体所经历的最好位置的适应度值相比较，取二者之中较优值作为群历史最优解；

（4）根据公式（3）和公式（4）更新粒子的速度和位置信息；

（5）如果收敛到最优解，则结束，否则执行步骤（2）。

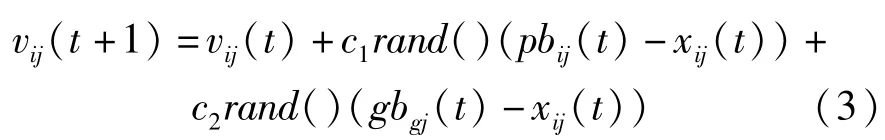
在算法的步骤（4）中考虑将粒子的最优位置搜索和种群的最优位置赋予一定的权重进行进化，并通过试验找出最佳权重因子，可以提高算法在最优解附近的搜索概率，使算法收敛速度和收敛精度提高。

4 适应度权重分配的粒子群优化K-means聚类算法

在优化的PSO算法过程中，每次迭代时根据聚簇的结果按照K-means算法求一次簇的中心，假设第i个聚类中心的均值mi表示为公式（5）

其中pj为簇Ci中第j个对象的位置；簇Ci中共有n个聚类对象。P为空间数据向量，在K-means算法聚类的过程中，适应度函数记为E（P），用P（t）表示在t次迭代搜索时的聚类中心，Po（t）表示已经搜索到的最优解，则有公式（6）和公式（7）：

E（P（i））=min（E（P（1）），E（P（2）），...，E（P（t）））

利用公式（8）对聚类中心进行调整：

P（t）= aK（P（t-1））+（1-α）Po（t-1）（8）

其中a是随机数，P（t-1）表示t-1时刻的聚类中心，P0（t-1）表示到t-1时刻搜索到的最优聚类中心，且a∈［0，1］。K（P（t-1））表示K-means变换，它将t-1时刻的聚类中心进行了均值优化。显然，当a =1时，公式（8）变化为经典的K-means算法。在算法的实际运行中，经过多次试验，发现a 取0.1时可以获得较好的效果。

利用改进的PSO算法结合K-means聚类，可以获得最好解的概率明显高于K-means方法和K-means + PSO方法。

新算法的流程如下：

（1）初始化粒子，随机生成簇中心并赋给各个粒子，随机产生粒子的速度；

（2）按最近邻法则对粒子进行划分，并按照公式（1）计算各个粒子的适应度值，更新个体极值；

（3）根据各个粒子的个体极值找出全局极值和全局极值位置，并按照公式（4）进行更新；

（4）按照粒子群优化算法的速度公式更新粒子的速度和位置，直至满足终止条件；

（5）输出最优粒子的位置，即最优的Nc个聚类中心。

5 试验结果

为了考察算法的性能，选择四组UCI数据集分别进行试验，分别为Iris、Wing、Zoo和Glass。Iris（鸢尾属植物）是一种基准函数数据集，被广泛用于模式识别和聚类分析测试。Iris数据集中，每组数据包含四种属性，分别表示Setosa、Versicolor和Virginica三种植物的萼片长度、萼片宽度、花瓣长度、花瓣宽度等；每种各有50组数据，共150个样本，数据为150*4维矩阵，其中1-50记录属于第一类Iris-setosa，51-100记录属于第二类Iris-versicolor，101-150记录属于第三类Iris-virginica。Wine数据集来自于意大利同一地区产的三种不同品种的葡萄酒，三类各有59、71和48个样本，共计178个。样本包含Alcohol、Malic acid、Ash等13种属性，为178*3矩阵。Zoo数据集为101种动物，这些动物属于7大类，每个类别包含的数量为4，5，8，10，13，2和41，该数据集为101*17维矩阵。Glass数据集有6类，每一类包含数量为70，76，17，13，9和29个样本，一共214个样本，该数据集为214*9维矩阵。

分别通过将改进的粒子群优化聚类算法和基本粒子群优化K-means聚类算法以及单纯的K-means聚类算法应用于该四组UCI数据，为了使计算结果更可靠，每组数据集分别计算50次，采用Visio Studio 6.0编译环境，C语言实现，最后取计算所得的平均值作为最终结论。计算结果如表1所示。

表1 三种算法的聚类特性比较

通过表1可以看出，改进的粒子群优化聚类算法与其他两种算法相比具有较高的准确率。在Iris 和Wine数据集中，改进的粒子群优化聚类算法与基本粒子群优化聚类算法相比较并没有明显的优势，但比单纯的K-means聚类性能优越；而在Zoo 和Glass数据集中，改进的粒子群优化聚类算法比基本粒子群优化聚类算法以及单纯K-means聚类算法均具有明显优势。该结论也表明本文提出的改进粒子群优化聚类算法在处理大数据集时具有更好的优越性。

6 结束语

聚类是数据挖掘最重要的任务之一，并且在未来相当长的时间内都具有重大的研究意义。提出了一种改进的具有适应度权重分配的聚类算法，通过将改进的粒子群优化算法与K-means算法相结合，PSO具有较强的全局搜索能力，可以克服K-means算法容易陷入局部最优的缺点。在改进的算法中，加入了适应度函数的权重分配，权重因子通过大量试验获得。

选用4组标准UCI数据，将改进的粒子群优化聚类算法与基本粒子群优化算法以及单纯K-means聚类算法分别应用于4组数据集的聚类中，并与标准聚类结果进行比较，通过比较各算法的聚类准确率，可以得出以下结论：

（1）改进的粒子群聚类算法具有更好的收敛效率和收敛精度；

（2）改进的粒子群聚类算法的平均聚类效率明显优于其他两种算法；

（3）改进的粒子群优化算法对于大数据集具有更好的收敛特性。

参考文献：

［1］Jiawei Han.M Kamber.Data Mining：Concepts and Techniques［M］.Los Altos，CA：Morgan Kaufmann Publishers，2001.

［2］姜园，张朝阳，仇佩亮，等.用于数据挖掘的聚类算法［J］.电子与信息学报，2005（4）：655-660.Jiang Yuan，Zhang Chaoyang，Qiu Peiliang.Clustering Algorithm Applying to Data Mining［J］.Journal of Electronic and Information，2005（4）：655-660.

［3］Clerc M.The Swarm and the Queen：Towards a Deterministic and Adaptive Particle Swarm Optimization［C］.In：Proc.1999 Congress on Evolutionary Computation.Washington，DC，Piscataway，NJ：IEEE Service Center，1999：1951-1957.

［4］高鹰，谢胜利.免疫粒子群优化算法［J］.计算机工程与应用，2004，40（6）：416-420.Gao Ying，Xie Shengli.Immune Particle Swarm Optimization Algorithm［J］.Computer Engineering and Application，2004，40（6）：416-420.

［5］高鹰，谢胜利.混沌粒子群优化算法［J］.计算机科学，2004，31（8）：13-15.Gao Ying，Xie Shengli.Chaos particle swarm optimization algorithm［J］.Computer Science，2004，31（8）：13-15.

［6］Parsopoulos K E.Stretching Technique for Obtaining Global Minimizers through Particle Swarm Optimization ［R］.Proceedings of the Workshop on PSO，Indianapolis：Purdue school of Engineering and Technology，INPUI，2001.

［7］王万良，唐宇.微粒群算法的研究现状与展望［J］.浙江工业大学学报，2007，35（2）：136-141.Wang Wanliang，Tang Yu.Research Status and Prospects of Particle Swarm Optimization［J］.Journal of Zhejiang University of Technology，2007，35（2）：136-141.

［8］Vance Faber.Clustering and the Continuous k-Means Algorithm［J］.Los Alamos Science，1994（22）：58-63.

［9］Mali U.Bandyopadhyay S.Genetic Algorithm-based on Clustering Technique［J］.Pattern Recognition，2000，33 （9）：1455-1465.

［10］OMRANGM，SALMAN A，ENGELBRECHTA P.Image classification using particle swarm optimization［C］.//Proc of the 4th Asia-Pacific Conference on Simulated Evolution and Learning.2002：

A New Optimization Clustering Algorithm of Improved Particle Swarm

Zhang Junxi1，Yang Haisu2
（1.Department of Vehicle Engineering，Xi’an Aeronautical University，Xi'an 710077，China；2.Xi'an Institute of Electronic Engineering，Xi'an 710100，China）

Abstract：K-means algorithm，widely used in the clustering analysis，uses the mean center of the heuristic information and has the advantage of high computational efficiency.But it is sensitive to the initial center and easy to fall into local optimum.PSO algorithm，with the parallelism and randomness characteristics，has greater superiority in massive database processing.It not only has strong global searching capability，but also enhances the searching probability around the optimal solution.And it reduces sensitive level of the initialization，so PSO algorithm can compensate deficiencies for K-means.The improved PSO algorithm is applied to K-means clustering algorithm which improves the stability and convergence efficiency of the algorithm.The experiments on four standard UCI datasets demonstrate that the new algorithm has more effectiveness.

Key words：K-means；Particle Swarm Optimization；Clustering Center；Stability；Searching；Converging；Sensitive

DOI：10.3969/j.issn.1002-2279.2016.02.016

中图分类号：TP311

文献标识码：A

文章编号：1002-2279（2016）02-0061-04

基金项目：❋陕西省自然科学基金项目（No.2014JM8353）

作者简介：张俊溪（1983-），女，河南省新乡市人，硕士研究生，讲师，主研方向：模式识别，智能系统。

收稿日期：2015-06-09