基于实际工况的零件公差规范设计方法*
2016-06-16孙永厚肖振泉黄美发
孙永厚,肖振泉,黄美发,张 骥
(1.桂林电子科技大学 机电工程学院,广西 桂林 541004;2.广西制造系统与先进制造技术重点实验室,广西 桂林 541004)
基于实际工况的零件公差规范设计方法*
孙永厚1,2,肖振泉1,黄美发1,2,张骥1
(1.桂林电子科技大学 机电工程学院,广西 桂林541004;2.广西制造系统与先进制造技术重点实验室,广西 桂林541004)
摘要:传统的零件公差规范设计一般只考虑功能要求和加工工艺,忽略实际工况的影响。针对以上不足,提出了一种基于实际工况的零件公差规范设计方法。首先依据小位移旋量(SDT)理论,建立零件公差数学模型;然后根据蒙特卡罗法求得实际要素的极限位置,生成模拟点并拟合得到规范表面模型,再转化为实体模型;最后通过有限元仿真,获得实际工况下的实体模型,对其进行规范操作,确定几何要素的最大偏差。通过实例分析,验证了该方法的可行性。
关键词:实际工况;蒙特卡罗;规范表面模型
0引言
零件公差规范设计是指设计工程师基于几何产品的功能要求,利用表面模型对实际工件表面进行模拟,对限定要素进行分离、提取、滤波、拟合等操作,确定在满足功能要求前提下几何要素的最大偏差,用来指导公差设计的过程。近年来,不少专家学者对零件公差规范设计进行了研究[1-3],但大多数研究只考虑零件的功能要求和加工工艺,忽略了实际工况的影响;而零件在实际工况下会承受工作载荷,由此造成的变形会影响到零件功能要求。因此,设计者在公差规范设计阶段需要考虑实际工况的影响,以便合理地设计公差。针对上述问题,在前人研究基础上提出一种基于实际工况的零件公差规范设计方法,综合考虑零件功能、加工工艺和实际工况的影响,通过一个实例阐述该方法步骤,验证该方法的可行性。
1传统零件公差规范设计
传统零件公差规范设计仅考虑零件功能要求和加工工艺的影响,忽略零件在实际工况下所受载荷,其主要步骤:
步骤1:建立公差数学模型。目前,大都采用小位移旋量(SDT)理论进行公差的统一表达。SDT理论的基本思想是将特征的几何缺陷看作是三维欧式空间中点集运动的结果,并应用微小矢量来表示点的空间运动,最早由 Bourdet 在1996年引入到公差领域[4]。SDT可以写成:
(1)
式中:θx、θy、θz表示理想要素绕X,Y,Z轴的转动;dx、dy、dz表示理想要素绕X,Y,Z轴的平动。根据SDT理论,首先求出理想要素的变动方程(以SDT分量为控制变量);然后根据公差约束条件,确定SDT分量的变动范围和约束条件,从而建立公差数学模型(此处的变动方程和SDT分量皆是关于公差域边界旋量参数)。
步骤2:确定公差带边界的位置。
步骤3:分析零件的功能要求对规范表面模型的影响。
步骤4:分析零件加工工艺对规范表面模型的影响,实际零件的误差主要与加工工艺有关,因此需要建立加工误差的数学模型。
步骤5:生成模拟实际工件的模拟点。
步骤6:对生成的模拟点进行插值或拟合操作,得到规范表面模型。
2基于实际工况的零件公差规范设计
实际工况下的零件公差规范设计方法步骤:①建立公差数学模型。②确定公差带边界的位置。③运用蒙特卡罗法求出实际要素在公差域中的极限位置。④考虑功能要求和加工工艺的影响,建立规范表面模型。⑤根据规范表面模型生成相应的实体模型。⑥分析实际工况载荷对规范表面模型的影响。下面仅介绍步骤中的③和⑥两步,其他步骤与传统零件公差规范设计方法类似,不再介绍。
2.1蒙特卡罗法求解实际要素的极限位置
公差数学模型只确定了公差域边界的变动范围和约束条件,并没有确定出实际要素在公差域的位置。本文需要求出实际要素在公差域中的极限位置(因为若实际要素处于极限位置情况下能符合功能要求,则其他位置也能符合功能要求);而求极限位置,关键是求实际要素旋量参数的极值。
蒙特卡罗法是一种直观高效的数值模拟方法,以数理统计和概率论为基础,在解决可靠性小样本数据和非线性复杂状态函数问题方面有比较好的效果[5]。因多种因素综合作用的影响,实际要素在公差域内具有随机性,因此实际要素的旋量参数是随机变量[6],能用蒙特卡罗法求其极值。以圆柱度公差(圆柱度公差域边界旋量参数仅需考虑θx1,θy1,dx1,dy1;同样地,实际要素旋量参数仅需考虑θx2,θy2,dx2,dy2[7])为例叙述具体求解步骤:
步骤1:确定公差域边界旋量参数θx1、θy1、dx1、dy1的理想概率分布模型,一般假定为正态分布。
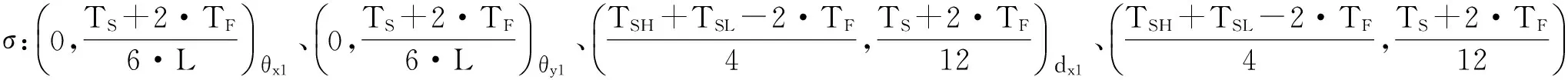
步骤3:对边界旋量参数进行抽样,获取实际要素旋量参数(θx2,θy2,dx2,dy2)的样本,抽样如图1所示。图中k为抽样次数,K为预定实际要素旋量参数样本数。至此,可得到K组实际要素旋量参数本。
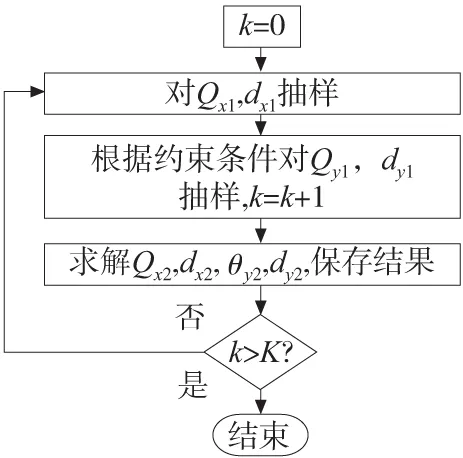
图1 抽样流程图
步骤4:进行实际要素旋量参数实际分布函数的假设检验,本文采用卡方拟合检验法。
步骤5:采用极大似然法估计实际分布函数的参数。
步骤6:求解实际要素旋量参数的极值根据参数实际分布函数类型与均方差,可求得参数的实际变动区间带宽:
(2)
则实际要素旋量参数的极值:
(3)
以上两式中:x=θx2、θy2、dx2、dy2,K为相对分布系数,e为相对不对称系数[8]。
2.2分析实际工况载荷对规范表面模型的影响
求得实际要素旋量参数的极值后,根据加工工艺和功能要求生成模拟点,对模拟点进行拟合生成规范表面模型;下面分析实际工况对规范表面模型的影响。
(1)有限元分析。首先根据规范表面模型生成三维实体模型;然后对三维实体模型进行实际工况载荷下的有限元分析,得到实际工况载荷下的变形体。
(2)获取带有变形信息的点。
①提取实体模型变形前的点集,这需要用到新一代GPS标准中分离与提取两种要素操作。在对三维实体模型进行有限元分析时,会在模型表面生成足够多个有限元节点,且模型具有近乎规则的几何特征,因此分离与提取等价于提取有限元节点;并且若有限元分析无误,节点中不会存在奇点,一般不需要进行滤波操作,这将大大减少工作量。
②获取各个节点在X,Y,Z坐标方向上的变形量,并提取的有限元节点坐标进行叠加处理,得到带有变形信息的一组数据点。
③对带有变形信息的数据点进行误差评价,获得实际工况载荷下实体模型最大几何偏差。
3算例分析
如图2所示,尾座顶尖由3个零件组成,其中对零件3的圆柱面有圆柱度公差要求;圆柱度公差值TF为0.003mm,直径d为100mm,上偏差TSH为0,下偏差TSL为-0.004mm,尺寸公差TS=TSH-TSL=0.004mm,长度L为200mm[9]。下面分别介绍基于实际工况的零件公差规范设计方法和传统零件公差规范设计方法。
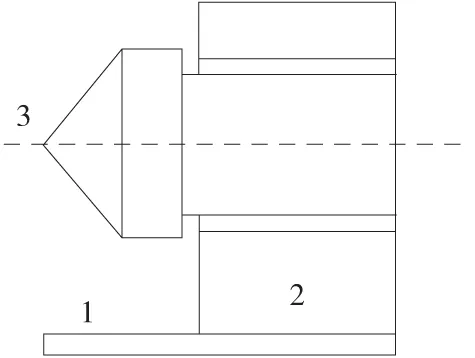
图2 机床尾座顶尖示意图
3.1基于实际工况的零件公差规范设计方法
3.1.1建立圆柱度公差数学模型
根据SDT理论,圆柱度公差数学模型[7]如下所示:
变动:
(4)
(5)
(6)
(7)
约束:
(8)
(9)
代入数据,可得:
变动:
(10)
约束:
(11)
3.1.2蒙特卡罗法求解实际要素极限位置
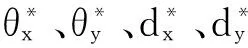
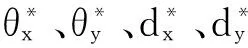
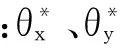
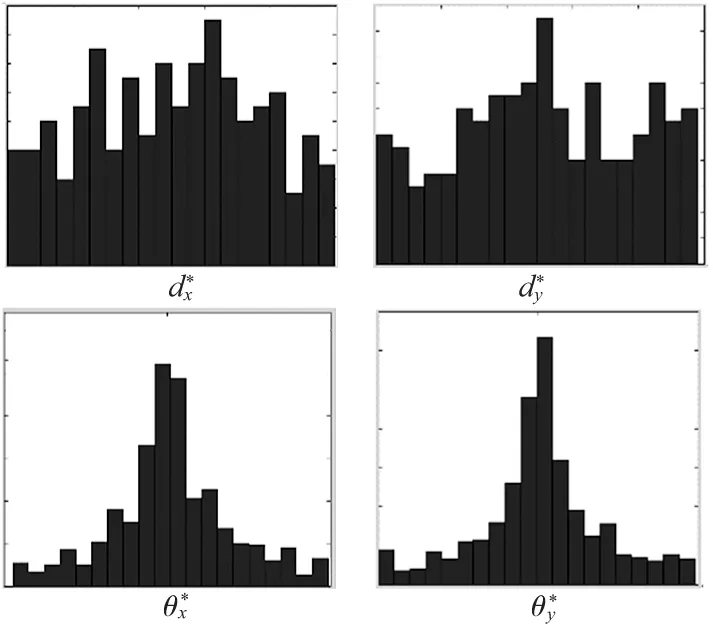
图3 实际要素旋量参数频数直方图
(3)求实际要素旋量参数的极值。
(12)
(13)
(14)
3.1.3生成规范表面模型
(1)零件的功能要求。对于本例中的顶尖,满足其公差值就能满足功能要求。
(2)加工工艺的影响。圆柱形零件经加工后会形成四种类型的圆柱面:锥形、凹形、凸形、香蕉形。对于顶尖插入端,经加工后会产生凸形圆柱面,加工误差:
Δt=A-B·(3·z2-1)
(15)
A,B为常数(根据具体公差值选取),z为零件轴线上的坐标值[2]。本例顶尖插入端的圆柱度公差为0.003mm,可取A=-0.0000001,B=0.0000001。
(3)在圆柱度公差域内生成模拟点。根据加工误差生成模拟点,如4图所示。
(4)生成规范表面模型。根据模拟点生成顶尖插入端的规范表面模型,如5图所示。
3.1.4分析实际工况对规范表面模型的影响
(1)有限元分析。建立顶尖实体模型时,插入端按上述规范表面模型生成实体模型,其余部分按理想情况建模;对顶尖实体模型进行实际工况载荷的有限元分析,得到其变形情况,如图6所示。
(2)分析实际工况对规范表面模型的影响。由于本例仅分析顶尖插入端圆柱面的圆柱度误差,因此只需提取插入端圆柱面的节点以及节点位移信息,将两者相加便可得到变形后的节点坐标。对变形点数据进行规范操作,评估结果:0.0032mm,并以此值修正初始公差值。

图4 模拟点

图5 规范表面模型
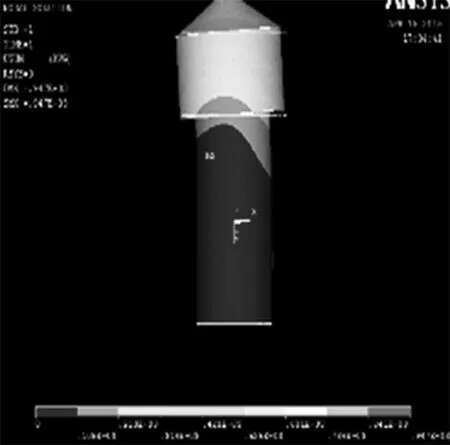
图6 顶尖变形云图

图7 规范表面模型
3.2传统公差规范设计方法
具体步骤参照第2节。首先根据公差数学模型,生成符合变动不等式和约束条件的边界旋量参数值:θx=-0.0000026564,θy=-0.0000036133,dx=-0.0036,dy=-0.0022。然后根据零件功能和加工工艺,生成体现误差的模拟点;最后拟合模拟点生成规范表面模型,如图7所示;并对其进行操作,评估结果:0.0025mm。
3.3分析结果比较
根据两种零件公差规范设计方法,分别进行10次公差规范设计,编写相应程序得到相应圆柱度误差值,如图8所示,图中横坐标表示规范设计的次数,纵坐标表示相应次数的圆柱度误差值;对所得结果进行分析,如表1所示。
由分析结果可知,实际工况载荷使顶尖圆柱度误 差期望值增大了28.7%,方差(波动)增大了35.4%,并且期望值超出初始设定公差值;可见,顶尖的实际工况载荷对规范设计结果之一─规范特征值产生很大的影响,也间接影响了测量、认证相关规范的制定。因此,对于精密机械系统而言,实际工况载荷不可忽视,在公差规范设计时,将其作为重要因素考虑,可真实地预测零件在实际工作环境下的变形,以便制定出合理的GPS规范。
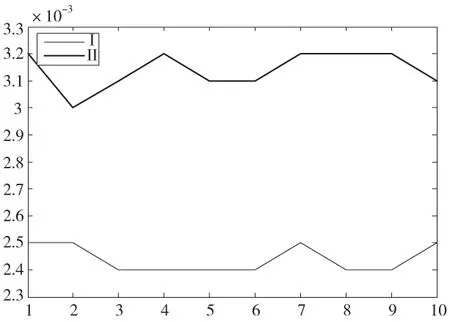
图8 两种方法结果

规范设计方法类型期望/mm方差/mm传统公差0.002440.00004899实际工况0.003140.000066332
4结束语
以SDT理论和蒙特卡罗法为基础,提出了一种基于实际工况的零件公差规范设计方法;以某车床尾座顶尖为例,分别应用本文提出方法和传统零件公差规范设计方法,对比了二者的规范设计结果,验证了本文提出方法的可行性与合理性,使公差的规范设计符合工程实际情况。
[参考文献]
[1] 李向前.基于新一代GPS的形状公差规范设计方法研究[D].桂林:桂林电子科技大学,2010.
[2] 周鑫.基于GPS的典型几何特征数字化建模及规范设计研究[D].郑州:郑州大学,2012.
[3] 彭娟.基本恒定类表面模型及操作算子的研究[D].桂林:桂林电子科技大学,2010.
[4] Bourdet P, Clement A. A study of optimal criteria identification based on the small displacement screw mode [J]. Annals of the CIRP, 1988, 37: 503-50.
[5] 庹奎,胡启国,谢国宾. 基于ANSYS的连杆结构强度混合可靠性分析[J]. 组合机床与自动化加工技术,2014(6):113-114.
[6] ZHONG Xin, YANG Ruqing, ZHOU Bing. Accuracy analysis of assembly success rate with Monte Carlo simulation [J]. Journal of Donghua University, 2003, 20(3): 128-131.
[7] 张娇娜.基于GPS标准体系的形状公差建模及其误差评价技术[D].杭州:浙江大学,2007.
[8] 王先逵. 机械制造工艺学[M].北京:机械工业出版社,2013.
[10] 王兆证.计算机辅助尺寸公差设计的研究[D]. 南京:南京农业大学,2002.
(编辑赵蓉)
The Specification Design of Tolerance Based on Working Load
SUN Yong-hou1,2, XIAO Zhen-quan1, HUANG Mei-fa1,2, ZHANG Ji1
(1.School of Mechanical and Electrical Engineering,Guilin University of Electronic and Technology, Guilin Guangxi 541004,China;2.GuangXi Key Laboratory of Manufacturing System &Advanced Manufacturing Technology, Guilin Guangxin 541004,China)
Abstract:Generally, the traditional specification design of tolerance of part only considers functional requirements and processing of part, ignoring the effect of the actual working situation. Faced with the lack above, a method of specification design of tolerance of part based on the actual working situation is proposed. Firstly, a tolerance mathematical model is built according to the theory of Small Displacement Torsor (SDT). Then, extreme position of actual feature is got by Monte Carlo method. Simulation points are produced and Specification surface model is obtained by fitting, which is next translated into solid model. Finally, solid model under the actual working situation is gained by finite element stimulation, whose specification operation is proceed to determine the maximum deviation of geometrical feature. The feasibility of proposed method is verified by an analysis of example.
Key words:the actual working situation; monte carlo; specification surface model
文章编号:1001-2265(2016)05-0009-04
DOI:10.13462/j.cnki.mmtamt.2016.05.003
收稿日期:2015-06-03;修回日期:2015-07-16
*基金项目:国家自然科学基金(51365009);广西制造系统与先进制造技术重点实验室主任课题(13-051-09-009Z)资助项目;桂林电子科技大学研究生教育创新计划资助项目(GDYCSZ201445)
作者简介:孙永厚(1967—),男,山东沂水人,桂林电子科技大学教授,工学硕士,研究方向为现代设计与制造技术、新一代GPS标准体系理论以及故障诊断专家系统,(E-mail)zyx881123@163.com。
中图分类号:TH161+.21;TG506
文献标识码:A
