双足步行机器人坡度切换控制
2016-06-16刘丽梅崔立芝吉林财经大学应用数学学院
刘丽梅 崔立芝吉林财经大学应用数学学院
双足步行机器人坡度切换控制
刘丽梅崔立芝
吉林财经大学应用数学学院
摘要:为了使带膝关节的双足步行机器人在不同坡度地面上都能稳定行走,本文提出了坡度切换控制策略。通过仿真实验验证了算法的有效性。
关键字:双足步行机器人 坡度切换 被动行走
1 引言
被动行走步态对机器人自身的结构参数和斜面倾角具有较强的依赖性,任何微小的扰动都能使步态偏离极限环,使机器人不能继续行走[1]。为了提高步态对地面环境变化的适应性,许多学者进行了相关研究。Spong等提出了势能整型控制和能量整型控制,扩大了机器人被动行走的斜坡范围[4]。Asano等提出了虚拟重力控制,使被动行走扩展到平面上[5]。Yong Hu等采用反馈线性化的方法设计了控制器,使机器人在坡度变化的路面上稳定行走[6]。强化学习方法也被应用到控制器的设计中,实现了非平坦地面上的稳定行走[7-8]。
2 带膝关节的双足步行机器人模型
带膝关节的双足步行机器人的周期步态由膝关节碰撞前的摆动过程、膝关节碰撞映射、膝关节碰撞后的摆动方程、摆动足与地碰撞映射四部分组成[9]。由牛顿-拉格朗日原理得摆动方程为,其中分别为各关节的角度,角速度和角加速度。τ为驱动力矩,若τ=0则为被动行走机器人。由角动量守恒原理得碰撞映射方程。整个周期步态是由连续微分方程和代数映射构成的一个混合系统。稳定的周期步态可以用极限环表示。
3 坡度切换控制
由于被动行走步态对坡度的变化比较敏感,因此当坡度发生变化后,为了使行走步态完成稳定的切换,本文提出了坡度切换控制。
当坡度从φ0变为f时,坡度切换控制分为两步:第一步,针对膝关节碰撞前的摆动方程
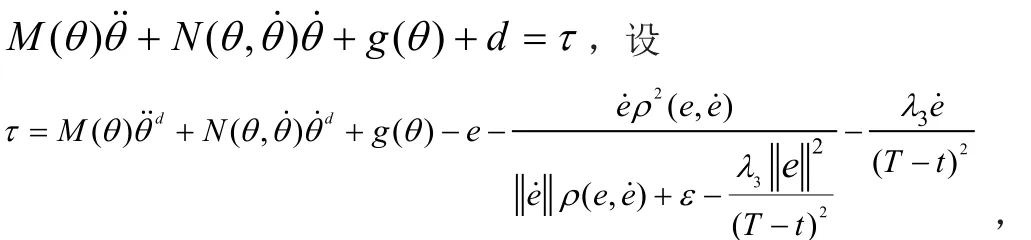
其中qd是以机器人摆动腿碰地后的状态为初始状态,以为目标状态设定的参考角位移轨迹,利用这个控制器实现在给定时间T内将机器人的步态切换到目标状态[10]。
第二步,在膝关节碰撞后摆动方程施加角度不变控制τ=[g(θ)- g (θ + φ- φ0)],即可使机器人完成不同坡度地面上的稳定行走。
4 仿真实验
仿真实验中机器人在坡度为3°的地面上向下被动行走5步,初始状态为[0.2044,-0.3091,-0.3091,-1.1171,-0.0628,-0.0628]T,到第6步地面坡度变为-3°,机器人摆动足碰地后的状态变为[0.2614,-0.2614,-0.2614,-1.0212,-0.0845,-0.0845]T,通过实验得到步态图1和图2。说明控制算法是有效的。
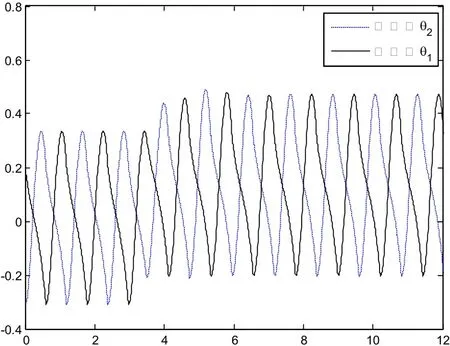
图1 坡度切换控制下机器人的角位移轨迹
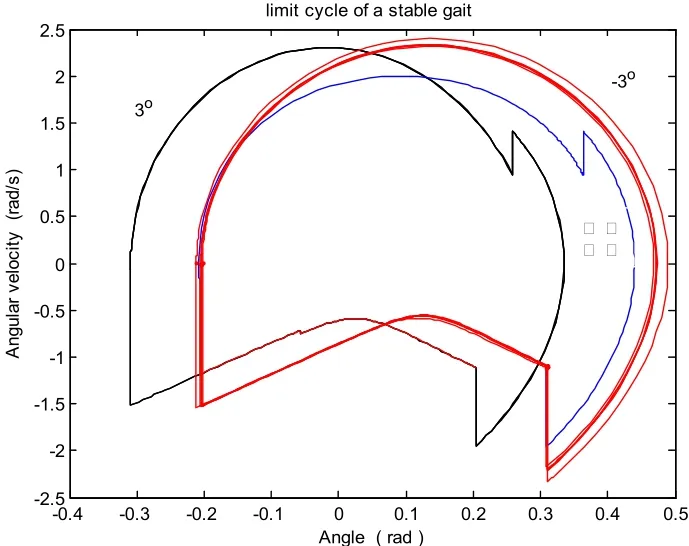
图2 变坡行走时步态的极限环图
5 结论
本文基于被动动力学原理,利用角度不变控制的优势,结合有限时间步态切换控制,提出了坡度切换控制。该控制算法扩大了机器人行走的坡度范围,提高了稳定步态对环境的适应性。通过仿真实验证明了算法的有效性。
参考文献
[1]Goswami A,EspiaBB. A study of the passive gait of a compass-like biped robot:symmetry and chaos[J]. International Journal of Robotics Research,1998,17 (12):1282-1301.
[2]M.W.Spong,F.Bullo.Controlled symmetries and passive walking[J]. IEEE Transactions on Automatic Control,2005, 50(7): 1025-1031.
[3]F.Asano,Z.W.Luo,M.Yamakita.Unification of dynamic gait generation methods via variable virtual gravity and its control performance analysis[C]. Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems,Sendai, Japan, 2004:3865-3870.
[4]毛勇,李实,王家,贾培发,杨丘振. 基于再励学习的被动动态步行机器人[J]. 清华大学学报(自然科学版), 2008,48(1):92-96.
[5]R.Tedrake,T.W.Zhang,H.S.Seung. Stochastic policy gradient reinforcement learning on a simple 3D biped[C]. Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems, Sendai, Japan, 2004:2849-2854.
[6]Yong Hu,Gangfeng Yan,Zhiyun Lin. Stable walking for a compass-like biped robot in complex enviroments[C]. 2010American Control Conference, Marriott Waterfront,Baltimore, MD, USA, 2010: 6048-6053.
[7]刘丽梅,田彦涛.双足机器人自适应常值驱动与传感反馈结合的仿生行走控制.控制与决策,2013,28(8):1152-1156.
[8]Limei Liu,YantaoTian, Zhen Sui,Xiaoliang Huang. Finit-time Robust Tracking control for the underactuated biped robot based on Poincare-like-alter-cell-to-cellmapping method. Proceedings of the 4th International Conference on Autonomous Robots and Agents, 686-691.
作者简介
刘丽梅,副教授,吉林财经大学应用数学学院,研究方向是复杂系统的控制与优化。
崔立芝,副教授,吉林财经大学应用数学学院,研究方向是复杂系统的控制研究。
基金资助
吉林省教育厅科学研究项目资助(吉教科合字[2014]第494号)。
