基于EMD-AWPP和HOSA-SVM算法的分布式光纤振动入侵信号的特征提取与识别

张燕君，刘文哲，付兴虎*，毕卫红

1. 燕山大学信息科学与工程学院，河北 秦皇岛 066004 2. 河北省特种光纤与光纤传感重点实验室，河北 秦皇岛 066004

基于EMD-AWPP和HOSA-SVM算法的分布式光纤振动入侵信号的特征提取与识别

张燕君1, 2，刘文哲1，付兴虎1, 2*，毕卫红1, 2

1. 燕山大学信息科学与工程学院，河北 秦皇岛 066004 2. 河北省特种光纤与光纤传感重点实验室，河北 秦皇岛 066004

针对传统的信号处理方法无法有效区分不同振动入侵信号，提出一种基于EMD-AWPP和HOSA-SVM算法的振动信息特征提取与识别方法，用于解决分布式光纤振动入侵检测系统的高精度信号识别问题。处理不同振动类型时，该方法首先利用基于经验模态分解的自适应小波包处理算法，不仅对信号的低频部分进行了分解，而且对高频部分即信号的细节部分也进行了更好的时频局部化处理，改善了信号特征提取精度，减少传感信号异常值的影响； 其次采用高阶谱分析中的双谱和双相干谱，精确提取包含不同振动入侵信号类型的特征矢量； 最后在BPNN参比模型的基础上，用粒子群算法优化SVM的识别参数，使识别模型具有更强的自适应和自学习能力，克服了神经网络易陷入局部最优的不足之处，实现不同振动入侵信号的特征矢量识别。分析结果表明，针对不同类型的入侵源识别，该方法可以有效剔除随机噪声的影响，提取传感信息的特征矢量，降低异常值的影响，算法的预测类别与输出类别几乎一致，振动识别的精确率达到95%以上，识别效果明显强于BPNN网络的检测算法，提高了信息分析的准确性。

分布式光纤传感； 经验模态分解； 自适应小波包； 高阶谱分析

引 言

近年来，分布式光纤振动入侵检测以其测量精度高、传感距离长、空间分辨率高等特点，在周界安防、管道运输和桥梁建筑等领域的识别检测、安全报警方面，能够精确识别出不同的振动入侵，且隐蔽性较强，克服了传统电子安全监测只有单一报警、缺乏危害识别的缺点[1-2]。而分布式光纤振动检测的关键是在噪声干扰的情况下能够精确的区分不同的振动入侵事件。因此，相应的光纤传感振动入侵信号的高精度信息提取与识别方法逐渐成为研究热点[3]。

在国外，Min等利用倒频谱平均消去法和非线性规模滤波法在频域上对入侵信号进行了特征提取，准确识别出了天然气管道上的异常事件； Seeddahmed等[4]提出了一种基于Level Crossings和神经网络算法的信号提取与分类方法，识别出了传感路径上的大降雨事件。在国内，饶云江等[5]利用小波分析法对信号进行去噪，并基于信号的边缘、峰值和功率谱对信号进行了特征提取； 喻骁芒等[6]提出了一种基于频带能量的特征提取方法，并通过反向传播神经网络识别出了常见的越境信号。然而，对于振动入侵传感信号，小波分析等方法存在信号本质特征的模糊提取和线性稳态缺陷的不足之处，信号的峰值、功率谱和频带能量等特征提取也会淹没在较强的高斯噪声环境中。

本研究提出了一种新的分布式光纤传感振动入侵信号特征提取与识别方法。该算法首先利用经验模态分解并结合自适应小波包(empirical mode decomposition with adaptive wavelet packet processing, EMD-AWPP)对信号进行异常值处理，降低噪声影响； 然后采用高阶谱分析(higher order spectral analysis, HOSA)对信号进行特征提取； 最后分别使用了粒子群优化后的支持向量机(support vector machine, SVM)和反向传播神经网络(back propagation neural network, BPNN)进行信号分类。结果表明，该方法可较好的提取振动入侵传感信号的信号特征，采用支持向量机进行振动入侵识别的精确率较神经网络具有更强的泛化能力。

1 基本原理

1.1 EMD-AWPP信号降噪原理

单模光纤中的传感信号非常微弱，加之伴随着光纤传感距离的增加，光纤链路远端发出的散射光信号经常会被噪声所淹没，变得难以检测。同时，振动信号通常具有频带范围宽和非线性、非平稳等特性。对于此类信号，短时傅里叶变换、小波变换等方法都存在信号分析的不适应、线性稳态缺陷和信号本质特征模糊提取等缺点。因此，提出了一种基于经验模态分解的自适应小波包去噪方法。

经验模态分解方法[7]根据信号的局部时变特性进行自适应处理，将信号分成不同的固有模态函数(intrinsic mode function，IMF)，IMF分量必须满足两个条件： 首先，分量的极值点个数和过零点个数最多相差一个或相同； 其次，分量的上下包络线关于时间轴局部对称。而相应的IMF分量可依据以下方法进行分解[8]。

(1) 确定信号的局部极值点，采用三次样条函数求得上下包络线m1(t)和m2(t)的均值。

λ1(t)=[m1(t)+m2(t)]/2

(1)

(2) 将信号x(t)减去上下包络线均值λ1(t)得y1(t)=x(t)-λ1(t)。

(3) 判定y1(t)是否满足IMF条件。如果不满足，则将y1(t)视为新的x(t)，重复上述步骤(1)和(2)，直到满足条件。

(4) 此时，可得到第一个IMF分量为c1(t)=y1(t)，余项为

r1(t)=x(t)-c1(t)

(2)

将r1(t)作为原始数据，进行同样的分解，依次得到IMF分量为c1(t)，c2(t)，…，直到ri(t)很小或成为一个单调函数时结束。因此，原信号可表示为

(3)

式中，余项rn(t)代表信号的平均趋势，IMF分量分别包含了信号从低到高的不同频段成分，且都是稳定的。

对于不同IMF分量采用自适应阈值的小波包算法进行处理[9]： 首先依据最小熵对信号进行分解，然后通过阈值函数对分解的高低频系数进行处理，最后对得到的估计小波包系数进行重构得到近似函数。常用的阈值函数包含软阈值和硬阈值[10]。然而硬阈值函数在阈值处不连续，导致重构信号振荡； 软阈值虽然连续性较好，可阈值前后小波包系数存在偏差，导致重构信号的边缘模糊，影响重构信号和真实信号的逼近程度。因此，在EMD分解的基础上，选择了一种自适应处理方法，如式(4)所示[11]。

(4)

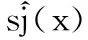
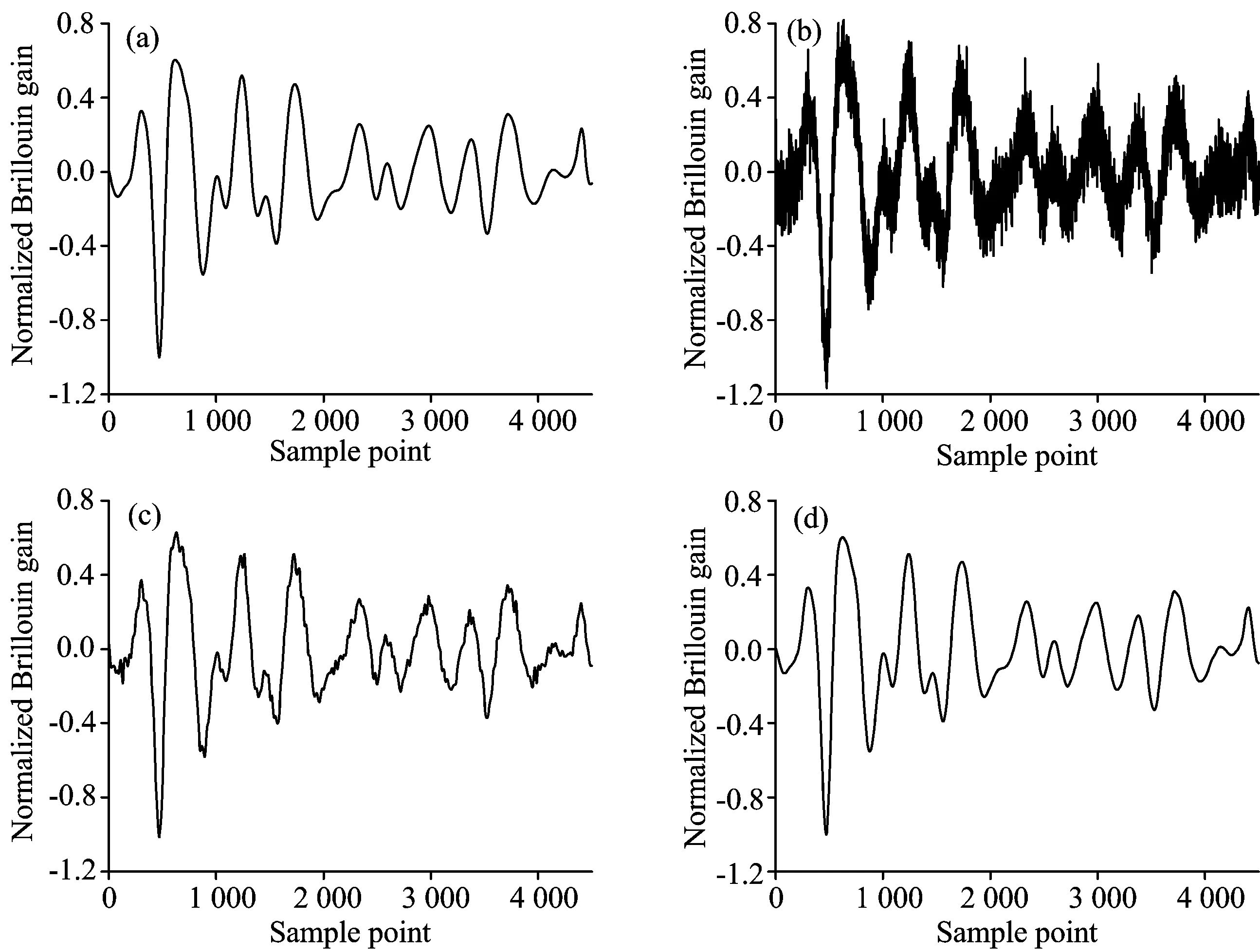
Fig.1 The Class one signal processing

Fig.2 The Class two signal processing

由图1和图2可得，自适应小波阈值去噪后的第一类和第二类信号虽能够较好地保留信号信息，但信号的细节部分较为粗糙； 而基于EMD分解的自适应小波包去噪方法不仅对信号的低频部分进行了分解，而且对高频部分即信号的细节部分也进行了更好的时频局部化处理，改善了信号特征提取精度。

1.2 HOSA-SVM信号识别原理

振动入侵检测的光纤传感信号是一种比较特殊的微弱信号，采用时频分析和滤波为主的信号特征分析方法容易丢失高阶的有用信息，很难达到令人满意的特征分析结果。因此，采用高阶谱分析方法对去噪后的传感信号进行信息提取。高阶谱分析[12]从较高的阶次上反映了不同的振动信号，并且理论上高阶谱完全能抑制高斯噪声，具有很强的消噪能力。

在高阶谱分析中，双谱包含了高阶谱的所有特性[13-14]，如双周期性、对称性等，并且双谱分析对高斯噪声不敏感，提高了传感系统测得的振动信号非线性特征提取的精确度。

在计算双谱估计的过程中，通过加窗函数对检测数据进行平滑处理，降低了估计误差。在传感信号处理中也可使用三阶累积量谱中的双相干谱进行信息提取，而双相干谱[15]可通过双谱归一化得到，

(5)

式中，B(w1,w2)为系统信号的双谱，P(w1)，P(w2)，P(w1+w2)分别为x(n)的功率谱在w1，w2，w1+w2处的值。相对于表示两个频率的能量谱的双谱，双相干谱的物理意义在于，体现了频率w1和w2相位耦合产生的能量在w1+w2处总能量中所占的比例。双相干谱函数的平方值b2在0和1之间，客观上描述了二次耦合的程度。若为0，即不存在相位耦合； 若为1，则w1+w2处的能量完全源于w1和w2的相位耦合。

基于上述特征提取后的结果，采用粒子群算法优化后的支持向量机对振动入侵信号进行分类识别，其中SVM通过选择某种非线性映射Γ将原空间中的输入量X映射到高维特征空间[16]，即

f(X)=wT×Γ(X)+b

(6)

式中，w为超平面权值问题，b为偏置项。在高维空间中，根据结构风险的最小化原则，构造最优决策函数，以克服神经网络容易陷入局部最小的缺陷[17-18]。

在SVM模型中，径向基函数是较常用的核函数，此时支持向量机的识别性能的准确率与惩罚因子c和相应的核函数参数g有关。基于上述分析，采用搜索能力较强的粒子群优化算法进行SVM参数选择。

粒子群算法(particle swarm optimization，PSO)是一种模拟鸟类捕食行为的仿生算法，它不断更新优化初始群体中的两个参数——个体最优解和群体最优解，以此得到整个空间的最优解[19]。粒子群中每个粒子对个体最优解Pbest和群体最优解Gbest的速度和位置按式(7)和式(8)不断的进行动态的调整和更新。

vij(t+1)=vij+c1r1(Pbesti(t)-xij(t))+

c2r2[Gbesti(t)-xij(t)]

(7)

xij(t+1)=xij(t)+vij(t+1)

(8)

式中，c1和c2为加速度常数(学习速率)；r1和r2为均匀分布的随机数；vij为第i个粒子第j个参数的当前速度；xij为第i个粒子第j个参数的当前位置。因此，基于粒子群参数优化SVM的振动识别过程如图3所示。

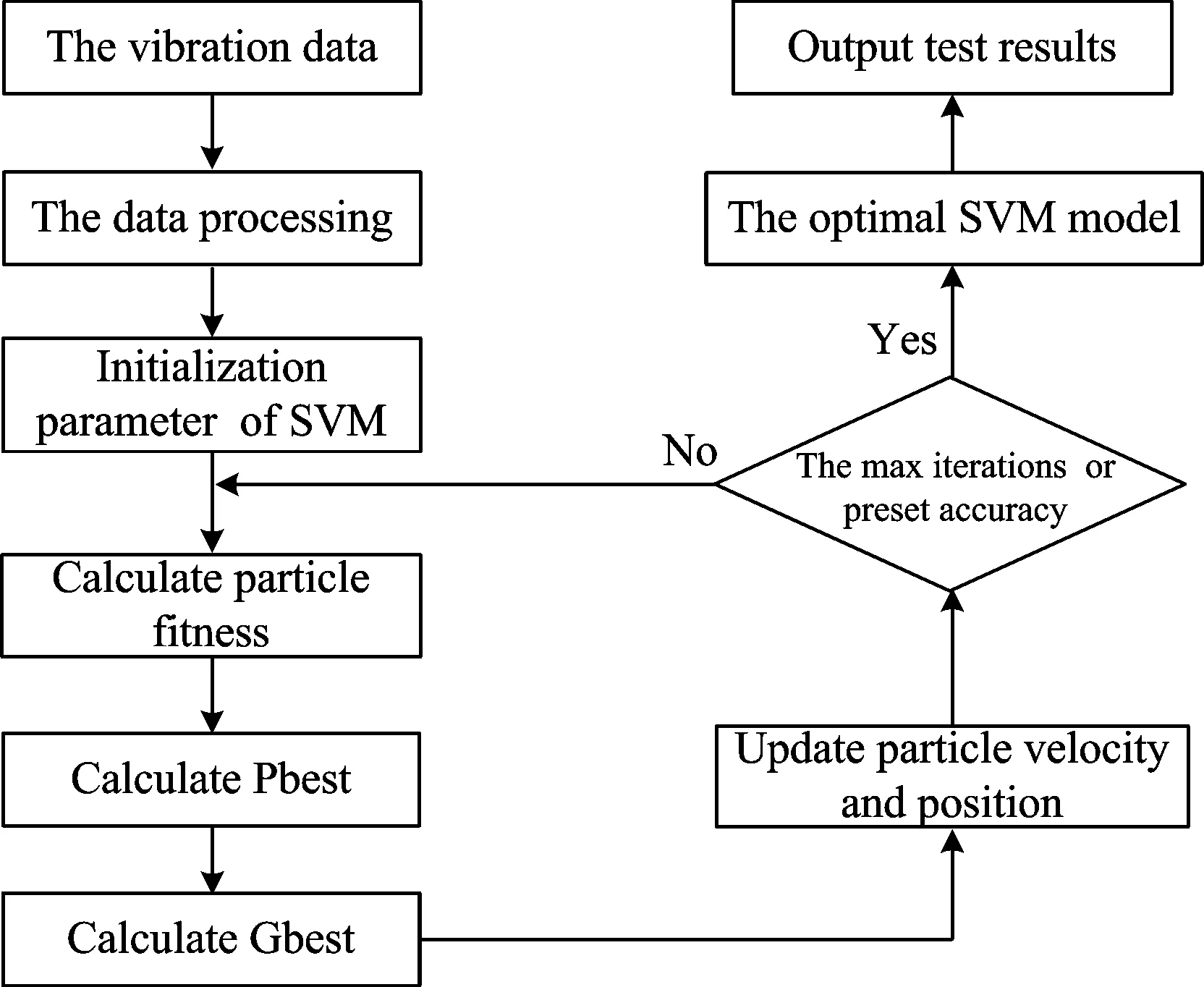
Fig.3 The detection process of SVM based on PSO algorithm

2 结果与讨论

为了验证所提出的分布式光纤传感振动入侵检测方法的有效性，设传感光纤在某一位置处分别受到了3种振动信号的影响。首先对振动入侵源进行分析，划分风险类别，然后通过EMD-AWPP和HOSA-SVM方法对获取的不同类型的训练样本和测试信号进行仿真识别。在不同振动入侵条件下，所采集到的第一类信号及其功率谱图、双相干谱图如图4和图5所示。

由图4和图5可得，在环境噪声很强，即低信噪比的情况下，功率谱反映不出第一类信号的有用信息，而不受非线性高斯噪声和加性高斯噪声影响的双相干谱分析可以准确地提取信息特征，明显提高了微弱信号的检测效果。此外，双谱分析在检测微弱信号也比传统的功率谱分析效果较好。下面对于经EMD-AWPP处理后的三种振动入侵信号分别进行双谱和双相干谱分析，双谱分析的二维结果如图6所示，双相干谱分析的三维结果如图7所示。

Fig.4 Low signal-noise ratio signal and its power spectrum

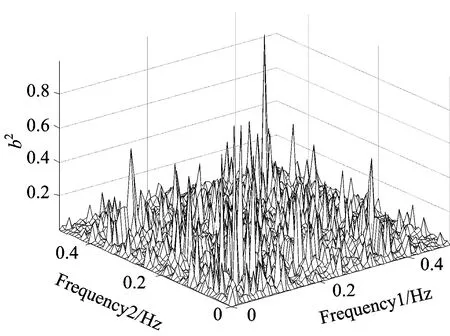
Fig.5 The bicoherence spectrum of low signal-noise ratio signal

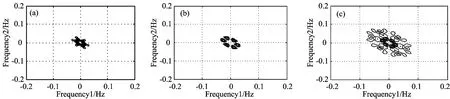
Fig.6 The bispectrum of different signal

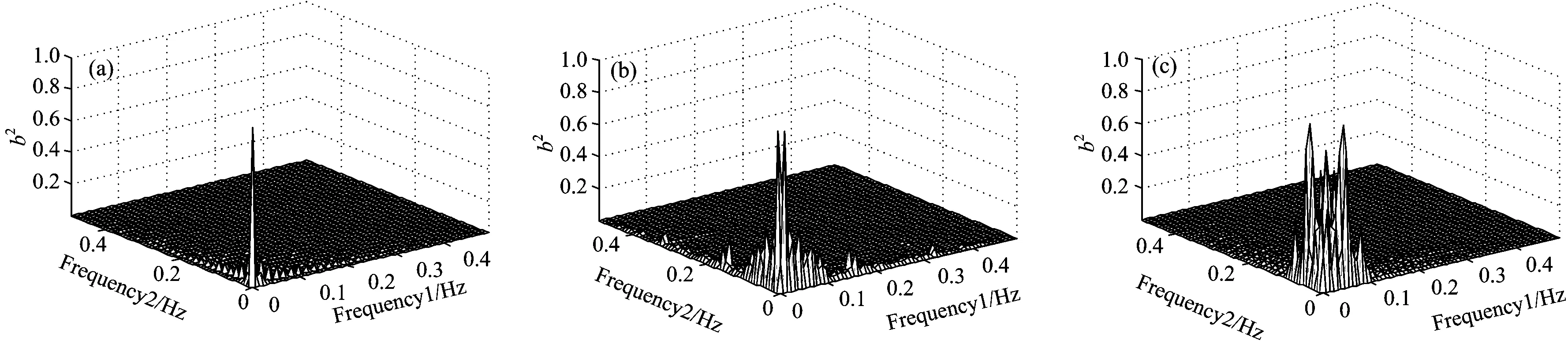
Fig.7 The bicoherence spectrum of different signal

由图6和图7可知，三种入侵源的分析结果存在着较为明显的差别。图6双谱分析的二维结果表明，第一类振动传感信号的非线性相位耦合现象主要集中在基频附近，表明在出现第一类振动前后，基带信号中的谐波成分没有出现变化，其他频率处趋于高斯特性，而第二、三类信号的非线性相位耦合逐渐体现在谐波成分上，且范围具有差异。图7双相干谱分析的三维结果表明，第一类信号只有一个波形极值点，即信号只在基频w1和w2处产生非线性相位耦合，且其能量占信号在w1+w2处总能量的比例较大，而第二、三类信号在若干频率分量处发生不同程度的相位耦合现象，峰值频率范围逐渐增大，非线性增强。通过高阶谱分析提取出来的三类信号的信息特征彼此也存在较大的区别，即利用双谱和双相干谱分析可以很有效的提取出不同信号的特征信息，利于传感信号的信息识别。

在每个振动源下各采集15组传感信号进行分析，提取10组经高阶谱分析后的幅值矢量作为信号特征量，分别用矢量(-1, 0, 1)的元素表示第一类、第二类和第三类的输出类型矢量，另外5组数据作为测试样本。

构建识别模型时，首先采用粒子群算法对SVM参数进行优化，其中PSO的粒子的种群数为25，最大迭代次数为200，学习因子分别为1.5和1.7。通过训练样本数据，得到识别模型中粒子的平均适应度和最佳适应度如图8所示，

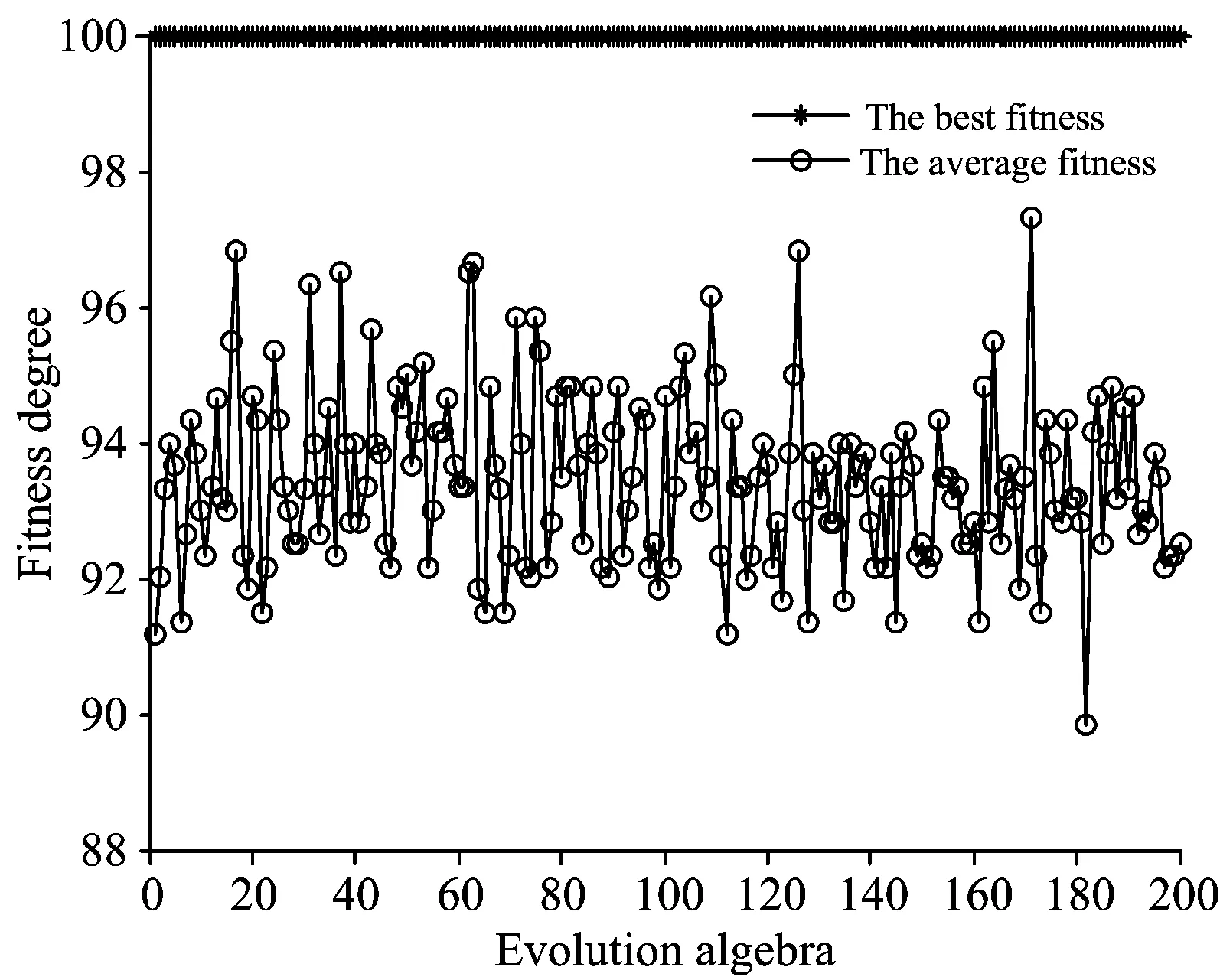
Fig.8 The fitness curve of Particle Swarm

虽然PSO参数寻优过程中利用了随机函数，致使训练测试得到的SVM参数略有不同，但其并不严重影响SVM对测量的正确识别。同时，采用反向传播神经网络(back propagation neural network, BPNN)作为优化后的SVM识别的参比模型，其对比结果如图9所示。

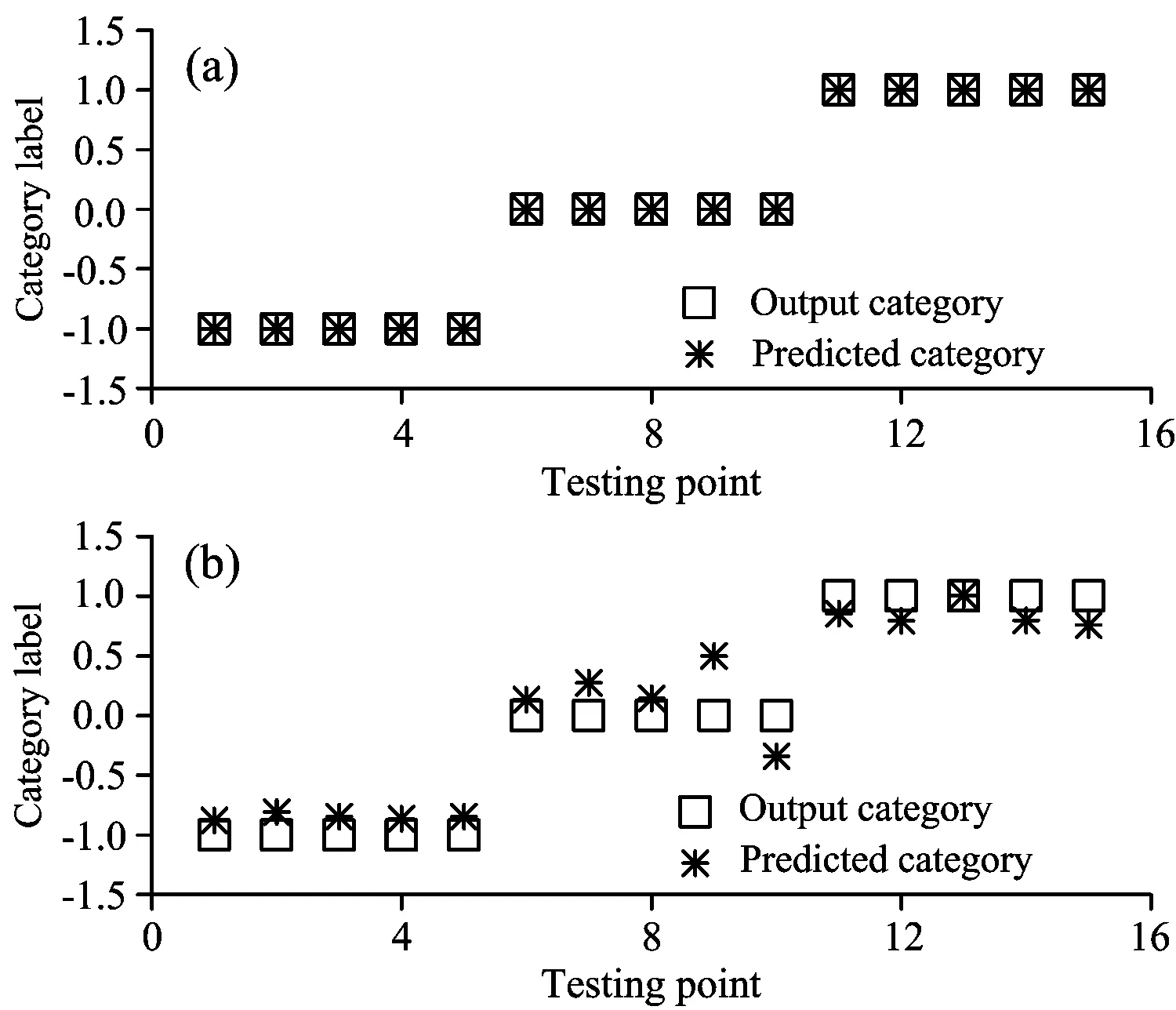
Fig.9 The result of testing recognition

由图9可以看出，针对不同类型的入侵源识别，采用SVM检测算法的预测类别与输出类别几乎一致，振动识别的精确率达到95%以上，识别效果明显强于BPNN网络的检测算法，并且SVM克服了神经网络易陷入局部最优的不足之处，更适用于振动入侵信号高识别率的要求。

3 结 论

以光纤为媒介对周围活动目标进行识别检测是基于分布式光纤传感的振动入侵检测系统的主要特点。该系统的传感信号为非平稳信号，采用传统的信号处理方法如小波分析和功率谱分析均不能有效区分不同振动入侵信号，且易淹没在噪声环境中。而本工作提出的基于EMD-AWPP和HOSA-SVM的振动信息的提取与识别方法，可很好地解决非平稳信号处理方法的不足。结果表明，该算法通过EMD自适应小波包算法解决了传统信号去噪精确度低的问题，而且使用高阶谱分析算法准确地提取出了包含传感信息的特征矢量，并在BPNN参比模型的基础上，用粒子群算法优化SVM的识别参数，使识别模型具有更强的自适应和自学习能力。因此，本算法可有效剔除随机噪声的影响，提取传感信息的特征矢量，同时高精确识别不同类型的振动入侵信号，提高了信息分析的准确性。

[1] Wu Huijuan, Rao Yunjiang, Tang Cheng, et al. Sensors and Actuators A: Physical, 2011, 167(2): 548.

[2] Zhou Zhengxian, Zhuang Songlin. Optics Communications, 2014, 33: 1.

[3] Wei Pu, Shan Xuekang, Sun Xiaohan. Optical Fiber Technology, 2013, 19(1): 47.

[4] Mahmoud S S, Visagathilagar Y, Katsifolis J. Photonic Sensors, 2012, 2(3): 225.

[5] RAO Yun-jiang, WU Min, RAN Zeng-ling, et al(饶云江，吴 敏，冉曾令，等). Chinese Journal of Sensors and Actuators(传感技术学报), 2007, 20(5): 45.

[6] YU Xiao-mang, LUO Guang-ming, ZHU Zhen-min, et al(喻骁芒，罗光明，朱珍民，等). Opto-Electronic Engineering(光电工程), 2014, 41(1): 36.

[7] Marco Leo, David Looney, Tiziana D’Orazio et al. IEEE Transactions on Instrumentation and Measurement，2012, 61(1): 221.

[8] David Looney, Danilo P. IEEE Transactions on Signal Processing. 2009, 57(4): 1626.

[9] Shao Renping, Hu Wentao, Wang Yayun，et al. Measurement, 2014, 54: 118.

[10] Hu Qiao, He Zhengjia, Zhang Zhousuo et al. Mechanical Systems and Signal Processing, 2007, 21: 688.

[11] LIU Heng-bing, HAN Shi-qin, LIU Jing(刘恒冰，韩世勤，刘 晶). Computer Engineering and Applications(计算机工程与应用), 2007, 43(24): 72.

[12] Jia Xiaoning, Yang Hang, Ma Siliang，et al. Optics and Lasers in Engineering, 2014, 57: 28.

[13] Kuang Chua Chuaa, Vinod Chandran, U Rajendra Acharyaa，et al. Medical Engineering & Physics, 2010, 32: 679.

[14] Liang B, Iwnicki S D, Zhao Y. Mechanical Systems and Signal Processing, 2013, 39: 342.

[15] QIU Su, JIN Wei-qi, SONG Zheng(裘 溯，金伟其，宋 铮). Optical Technique(光学技术), 2011, 37(3): 351.

[16] Helena G Ramos, Tiago Rocha, Jakub Král，et al. Measurement, 2014, 54: 201.

[17] Cheng Weifei, Guang Chenbai. Mechanical Systems and Signal Processing，2014, 49: 196.

[18] Sun Jiedi, Xiao Qiyang, Wenb Jiangtao，et al. Measurement, 2014, 55: 434.

[19] Behrang M A, Assareh E, Noghrehabadi A R，et al. Energy, 2011, 36: 3036.

*Corresponding author

An Extraction and Recognition Method of the Distributed Optical Fiber Vibration Signal Based on EMD-AWPP and HOSA-SVM Algorithm

ZHANG Yan-jun1, 2, LIU Wen-zhe1, FU Xing-hu1, 2*, BI Wei-hong1, 2

1. School of Information Science and Engineering, Yanshan University, Qinhuangdao 066004, China 2. The Key Laboratory for Special Fiber and Fiber Sensor of Hebei Province, Qinhuangdao 066004, China

Given that the traditional signal processing methods can not effectively distinguish the different vibration intrusion signal, a feature extraction and recognition method of the vibration information is proposed based on EMD-AWPP and HOSA-SVM, using for high precision signal recognition of distributed fiber optic intrusion detection system. When dealing with different types of vibration, the method firstly utilizes the adaptive wavelet processing algorithm based on empirical mode decomposition effect to reduce the abnormal value influence of sensing signal and improve the accuracy of signal feature extraction. Not only the low frequency part of the signal is decomposed, but also the high frequency part the details of the signal disposed better by time-frequency localization process. Secondly, it uses the bispectrum and bicoherence spectrum to accurately extract the feature vector which contains different types of intrusion vibration. Finally, based on the BPNN reference model, the recognition parameters of SVM after the implementation of the particle swarm optimization can distinguish signals of different intrusion vibration, which endows the identification model stronger adaptive and self-learning ability. It overcomes the shortcomings, such as easy to fall into local optimum. The simulation experiment results showed that this new method can effectively extract the feature vector of sensing information, eliminate the influence of random noise and reduce the effects of outliers for different types of invasion source. The predicted category identifies with the output category and the accurate rate of vibration identification can reach above 95%. So it is better than BPNN recognition algorithm and improves the accuracy of the information analysis effectively.

Distributed optical fiber sensing; Empirical mode decomposition; Adaptive wavelet packet; Higher order spectral analysis

Nov. 25, 2014; accepted Mar. 21, 2015)

2014-11-25，

2015-03-21

国家自然科学基金项目(61205068)，中国博士后科学基金项目(2013M541200)，河北省自然科学基金项目(F2014203125)，燕山大学“新锐工程”人才支持计划项目资助

张燕君，女，1973年生，燕山大学信息科学与工程学院教授 e-mail： yjzhang@ysu.edu.cn *通讯联系人 e-mail: fuxinghu@ysu.edu.cn

TN247

A

10.3964/j.issn.1000-0593(2016)02-0577-06