EMD时频分析拉曼光谱和近红外光谱
2016-06-15赵肖宇方一鸣
赵肖宇,方一鸣,谭 峰,佟 亮,翟 哲
1. 黑龙江八一农垦大学信息技术学院,黑龙江 大庆 163319 2. 燕山大学电气工程学院,河北 秦皇岛 066004 3. 齐齐哈尔大学通信与电子工程学院,黑龙江 齐齐哈尔 161006 3. 中国林业科学研究院华北林业实验中心,北京 102300
EMD时频分析拉曼光谱和近红外光谱
赵肖宇1,方一鸣2,谭 峰1,佟 亮3,翟 哲4
1. 黑龙江八一农垦大学信息技术学院,黑龙江 大庆 163319 2. 燕山大学电气工程学院,河北 秦皇岛 066004 3. 齐齐哈尔大学通信与电子工程学院,黑龙江 齐齐哈尔 161006 3. 中国林业科学研究院华北林业实验中心,北京 102300
用时频方法分析拉曼光谱和近红外光谱。经验模态分解光谱成为特征模态分量,模态分量比重计算显示拉曼光谱能量均匀分布于各个分量,而近红外光谱的低阶特征模态分量只承载了较少的原光谱有效信息。真实光谱和数值实验均显示,经验模态分解视拉曼光谱为调幅信号,具有高频能量吸附特性; 视近红外光谱为调频信号,在一阶特征模态分量中可以较好实现高频窄带解调。一阶特征模态分量希尔伯特变换显示,经验模态分解拉曼光谱时易出现模态混叠现象。进一步在时频域分析玉米叶片近红外光谱,经验模态分解后截掉低能量的一、二阶分量,用剩余特征模态分量重构光谱信号,均方根误差为1.001 1,相关系数为0.981 3,两个指标反映出重构精度较高; 分解趋势项表明在近红外光波段,吸光度随着波长的减小呈现递增趋势; 特征模态分量的希尔伯特变换显示,657 cm-1是碱胁迫光谱特有频率,可作为碱胁迫光谱特征频率来辨识。
时频分析; 经验模态分解; 希尔伯特变换; 近红外光谱; 拉曼光谱
引 言
透射率(T)、反射率(R)或者吸光度(A)相对于波长或波数的变化构成了近红外光谱; 拉曼光谱横坐标是散射光相对于入射光的波数差(拉曼位移),纵坐标是光子计数。事实上,根据波速、波长与频率关系,无论是拉曼还是近红外光谱都是频率谱图,可以借助傅里叶反变换得到对应时频谱,那么现有时频分析方法即可以用到光谱分析,操作细节有待进一步研究。近红外或拉曼光谱通过特征峰定性辨识某种分子结构或定量分析该成分,特征峰定位过程与寻找时间函数变异点过程相似,所以从谱图分析角度,可以直接将光谱视作时变函数处理,这样除了信号原有“时间”参量,通过时频方法处理,光谱还具备了“频率”参数,以及可以设计时间和频率联合函数,用它们表达光谱更多方面的信息。
经验模态分解(empirical mode decomposition,EMD)方法是美国国家宇航局美籍华人黄锷(N. E. Huang)等于1998年创造性提出新型的信号时频处理方法[1],该方法一经提出即得到了学术界的最广泛的关注。2009年出现基于EMD方法分解拉曼光谱并结合小波算法对特征模态分量(intrinsic mode function,IMF)去噪的研究,文献[2]对近红外导数光谱经验模态分解后针对低阶IMF阈值滤波,也可以直接去掉近红外原光谱中低阶IMF分量以实现滤波[3]。目前已有EMD方法在光谱预处理方面的应用,但就低阶IMF处理是否可以实现去噪,时频方法处理近红外光谱和拉曼光谱的区别以及EMD方法是否可以用于光谱定性和定量分析,这些涉及到光谱IMF属性的研究及其时频分析,至今依然未见报道。本研究的主要目的就是通过数值实验的手段,研究光谱EMD的一阶IMF时频属性,揭示EMD方法分解拉曼光谱和近红外光谱的差异性,并试图用光谱的希尔伯特变化(hilbert transform, HT)辨识光谱的特异性。
1 光谱采集
实验采用WQF-600N傅立叶变换近红外光谱分析仪,光源电压: 5 V,在10 000~3 500 cm-1光谱范围内以8 cm-1分辨率扫描32次,本底扫描64次。采用美国DeltaNu拉曼光谱仪Advandge532系列,激光激发波长为785 nm,连续输出功率120 mW,分辨率为8 cm-1,光谱采集范围200~2 000 cm-1,阵列CCD2048个像素。
人工温室环境下,水基培育玉米。玉米三叶一芯时采样,距离叶顶端5 cm处截取叶样(此处叶脉不明显并且平整),采集同一样品近红外光谱和拉曼光谱,如图1和图2所示。另一组样品采用碱胁迫培养(氢氧化钠)用来模拟大庆地区碱性生长环境,目测碱胁迫光谱图同图1和图2无差异。
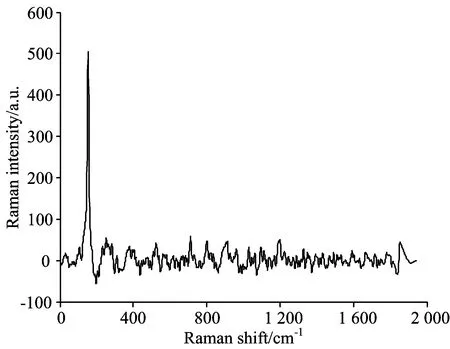
Fig.1 Raman spectrum of corn leaf
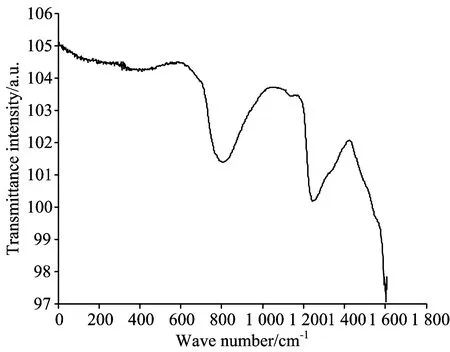
Fig.2 Near infrared spectrum of corn leaf
2 光谱EMD的高频能量吸附属性
记拉曼光谱和近红外光谱为l(ν)和i(ν),在安装有EMD Tool-box的Matlab2011b环境下经验模态分解拉曼光谱和近红外光谱,分别得到9和7个IMF分量,即
其中IMF为分解出来的调制窄带信号。
定义重量和比重函数来衡量分解分量的重要程度: 任意光谱分量IMFj重量
分量比重
分别计算拉曼光谱和近红外光谱的比重,如表1所示。
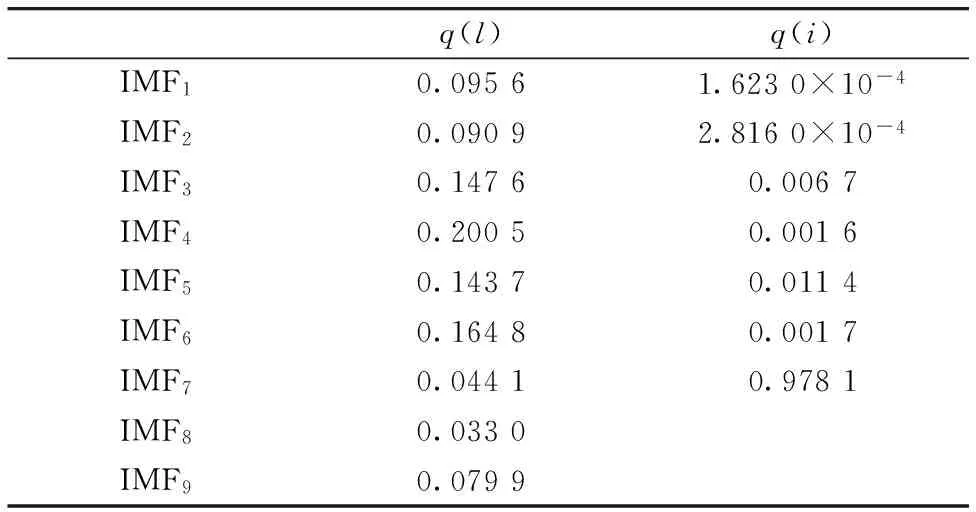
Table 1 Weight distribution of Raman spectrum and near infrared spectrum components
表中q(l)为拉曼光谱分量比重,比重分布范围3.3%~20.5%,能量分布均匀。
q(i)为近红外光谱分量比重,可以看出光谱中有效成分集中在IMF3~IMF7。
重点考察一阶IMF分量,如图3和图4所示,图中(a)为一阶IMF分量,(b)为扣除一阶IMF后剩余信号。
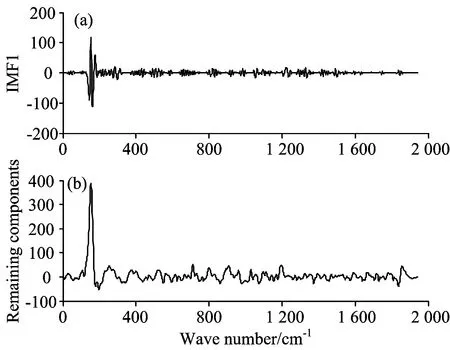
Fig.3 IMF1 and remaining components of Raman spectrum decomposed by EMD
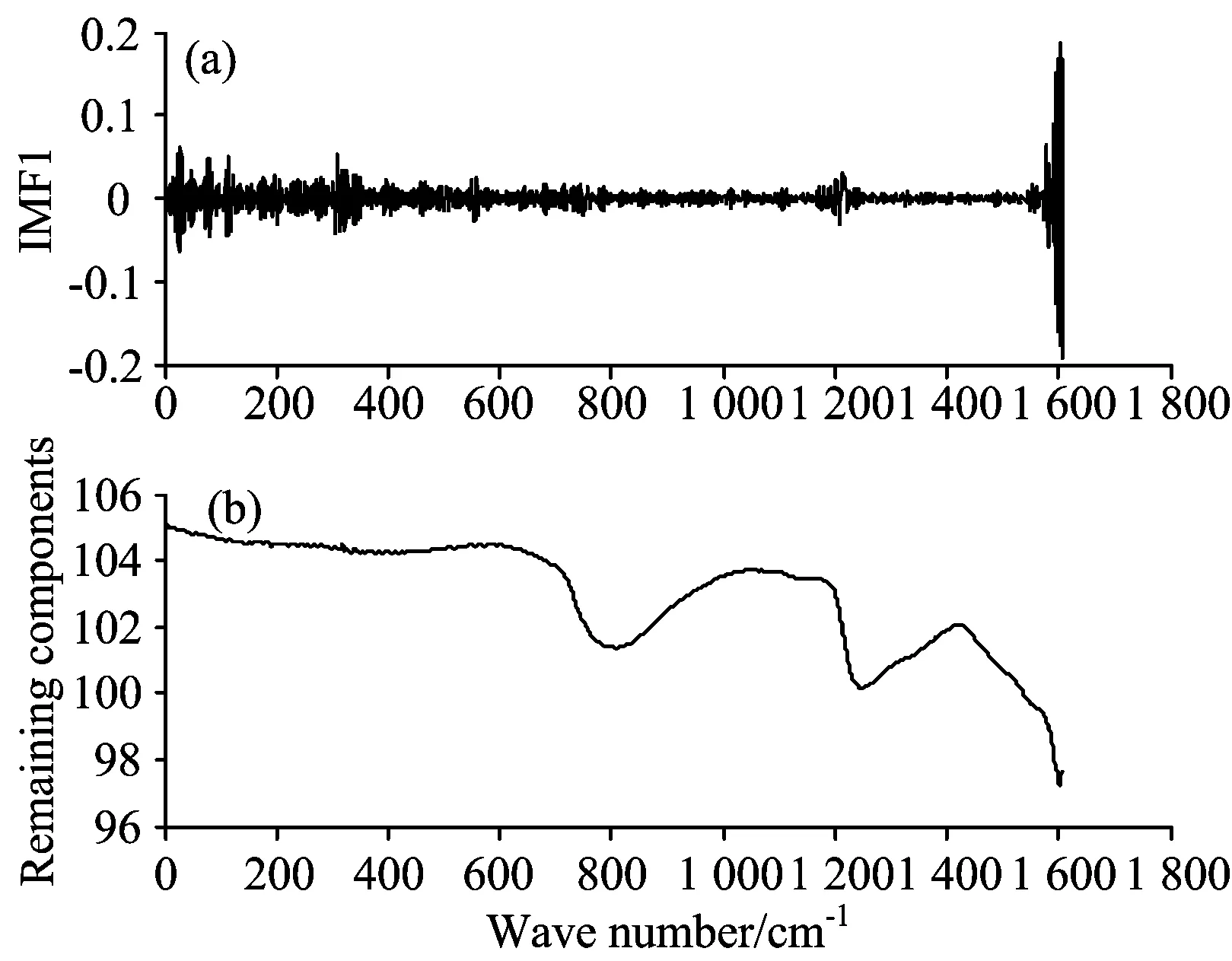
Fig.4 IMF1 and remaining components of near infrared spectrum decomposed by EMD
通过图1和图3的剩余分量部分对比观察,EMD对拉曼光谱幅值改变很大,即EMD基本上将拉曼光谱视作AM(amplitude modulated)调制信号,拉曼光谱中的大部分能量吸附到第一阶IMF中; 从图2和图4看到,EMD对近红外光谱幅值改变不大; 图4中,IMF1是绝对高频信号,剩余分量是相对低频信号,EMD将近红外光谱信号视作FM(frequency modulation)信号。这样的结论是否准确呢?
两类光谱的区别是近红外为低频信号,拉曼为高频信号。信号采集过程,光谱中都会引入噪声信号。考虑使用两个单频率信号分别模拟理想光谱信号和噪声信号,其表达形式如下:
S(n)=A1cos(2πf1n),N(n)=A2cos(2πf2n),X1(n)=S(n)+N(n),X2(n)=S(n)×N(n),为了更好地模拟光谱与噪声,设定A1/A2=1 000;X1可以表示一部分幅度调制信号,用来模拟拉曼信号,其中光谱信号与噪声信号频率相对接近f1/f2=0.8; 用X2表达近红外信号,是一个调频信号,其中f1/f2=0.005。拉曼和近红外模拟信号如图5和图6所示。
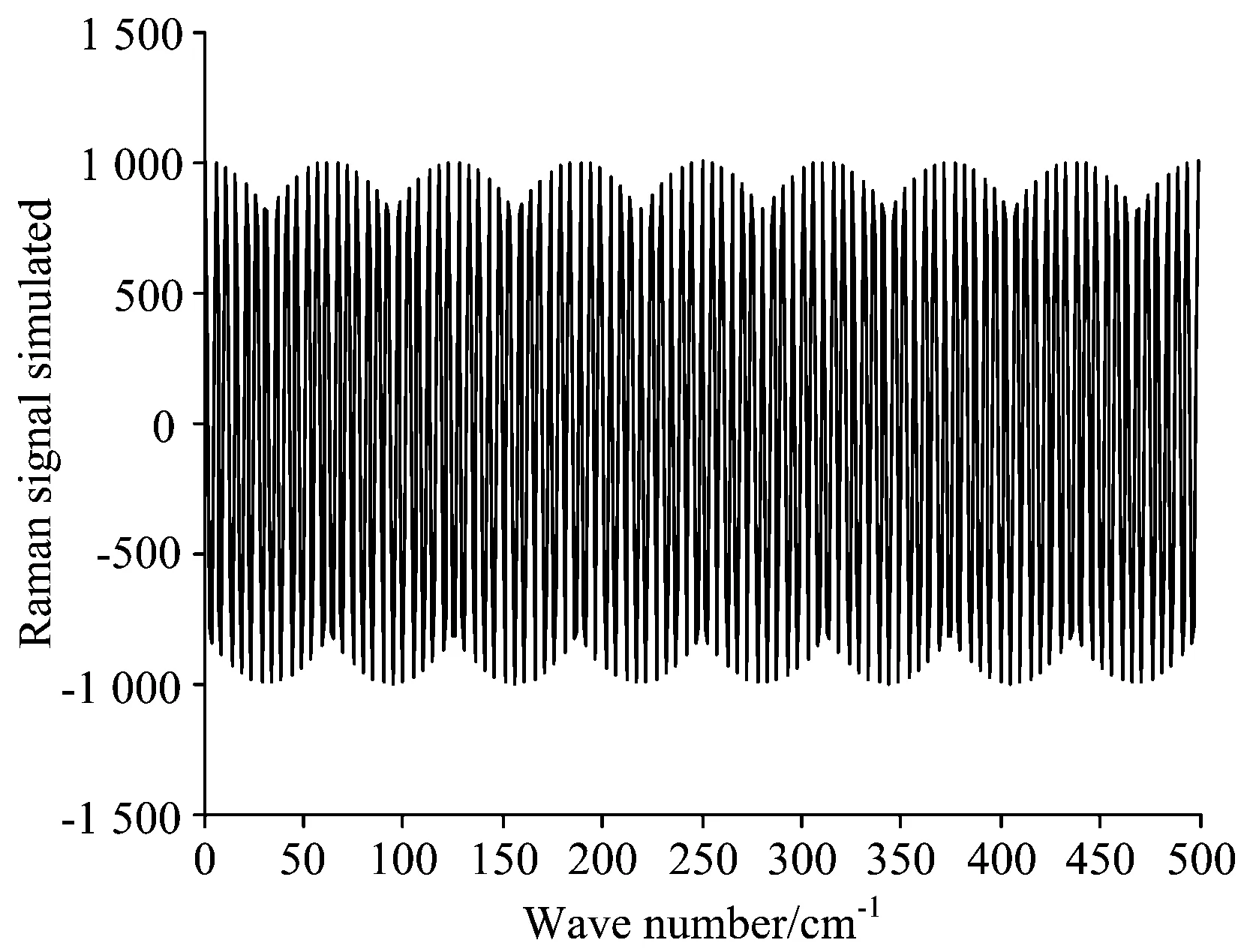
Fig.5 Ideal Raman spectrum
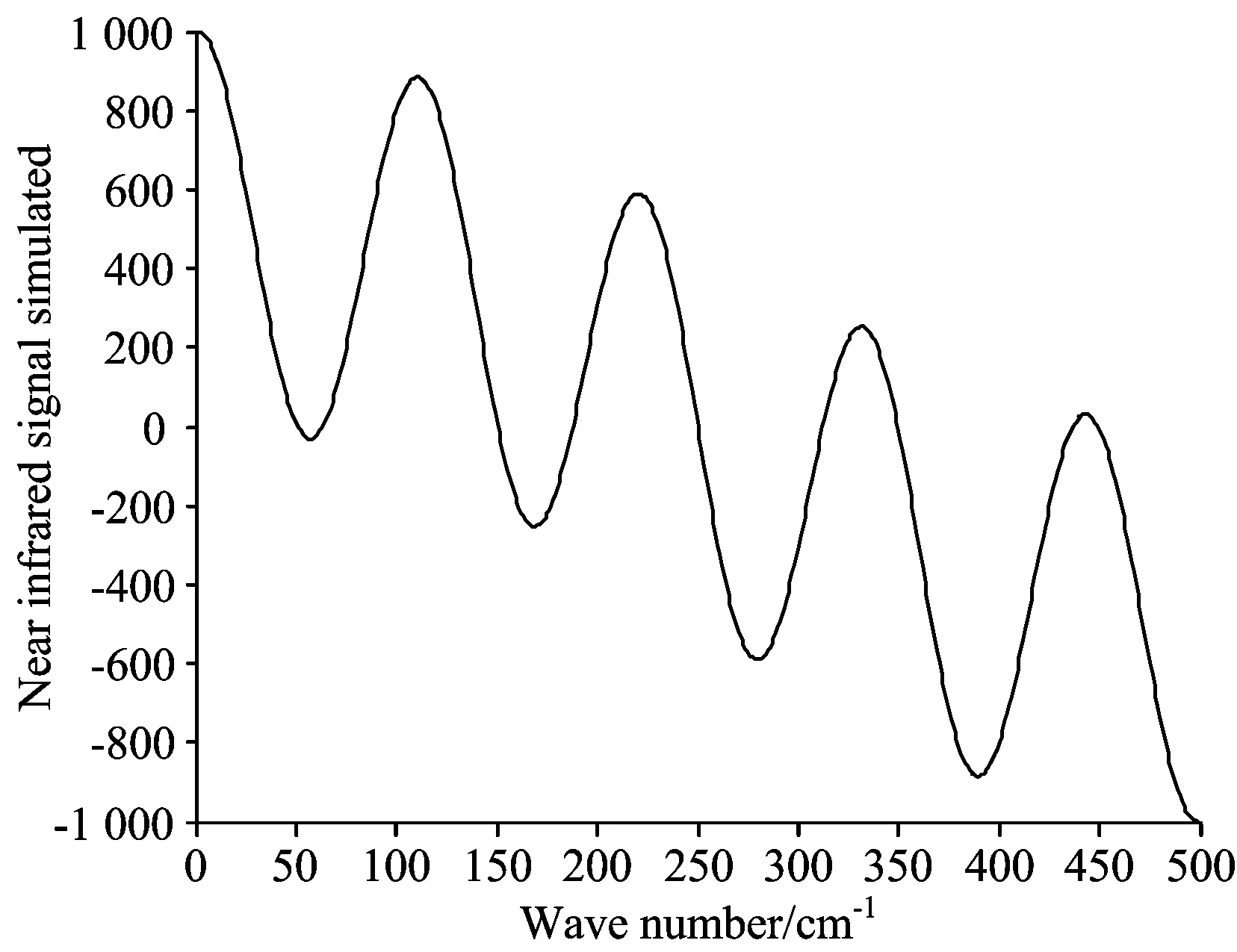
Fig.6 Ideal near infrared spectrum
EMD分解如图7和图8所示。
图7中的幅值情况再一次说明了拉曼模拟信号中大部分能量被吸附到一阶IMF中,称为高频能量吸附特性,这时EMD更多的视拉曼光谱为AM信号; 图8中IMF1频率比剩余分量高,IMF1基本保持了噪声性状,EMD视近红外光谱为FM信号。
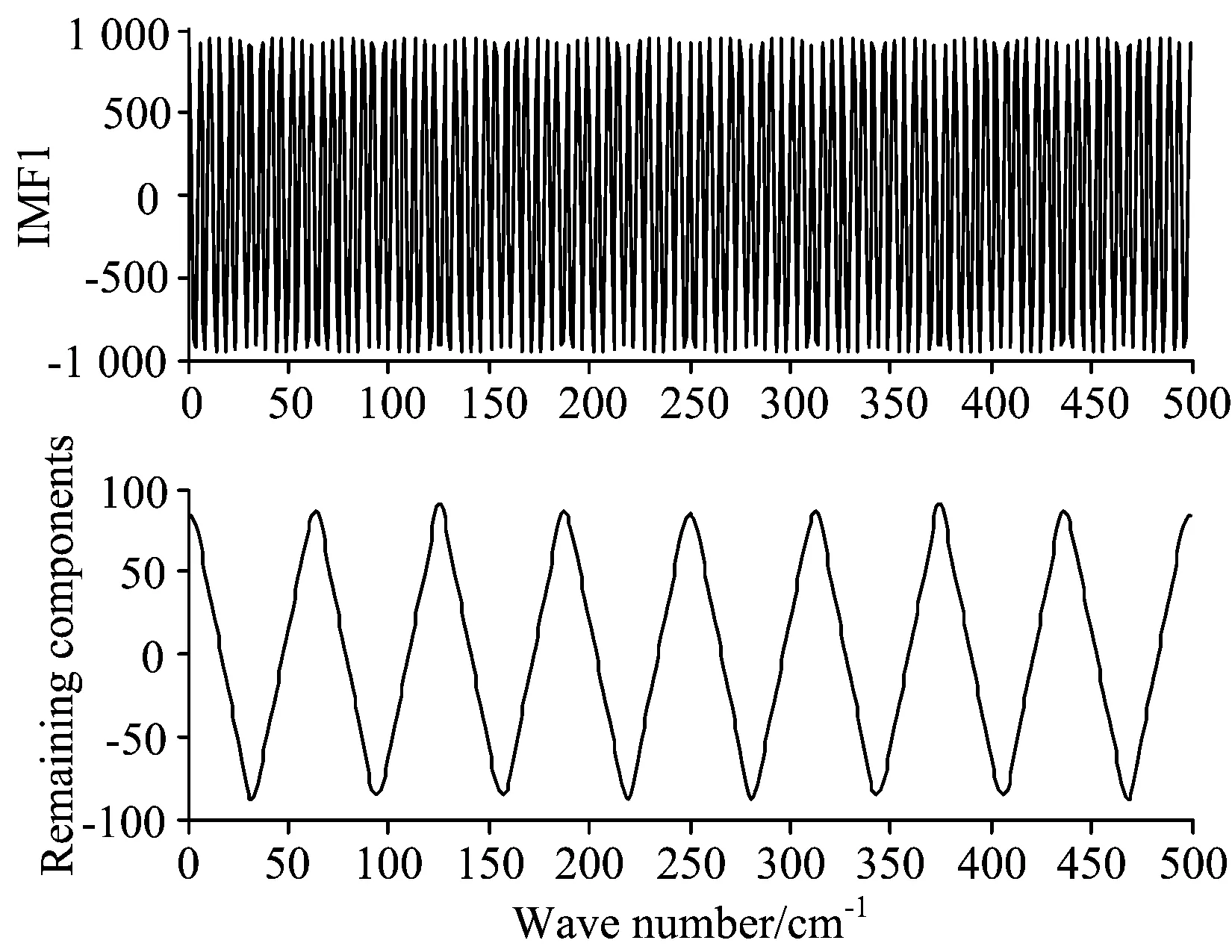
Fig.7 IMF1 and remaining components of ideal Raman spectrum decomposed by EMD
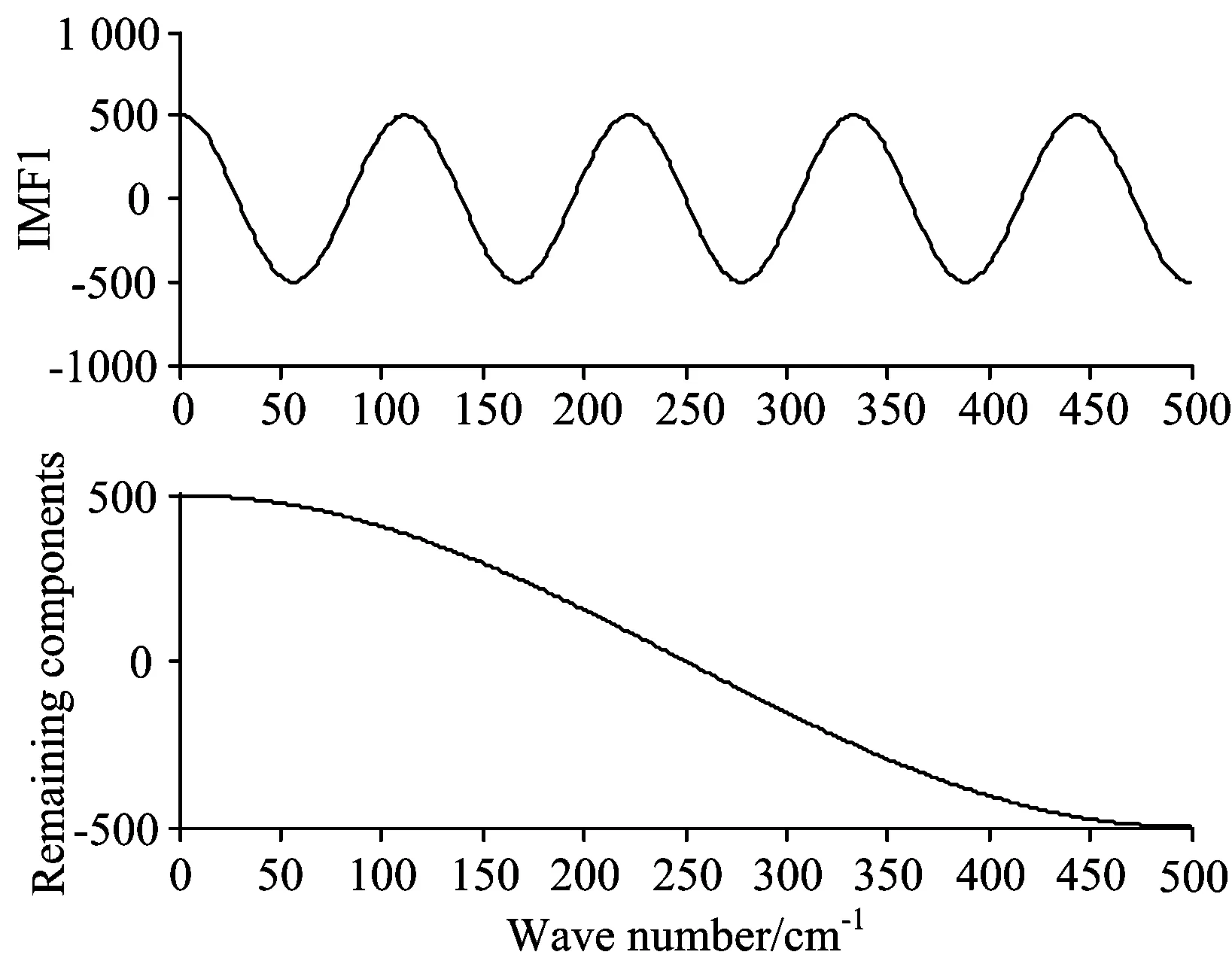
Fig.8 IMF1 and remaining components of ideal near infrared spectrum decomposed by EMD
通过以上实验得出,对拉曼光谱的低阶IMF低通滤波、阈值滤波或者直接截掉低阶IMF以实现去噪,会使拉曼光谱能量损失很大,光谱形变; 用上述方法处理近红外光谱结果差异很大,可以实现简单快速去噪。
3 光谱模态混叠现象
EMD的实质是按照信号的频率,以特征尺度为依据解析信号为IMF分量,这意味着IMF为短时单频率组分信号。拉曼和近红外光谱EMD分解后,对一阶IMF希尔伯特变换,瞬时频率如图9和图10所示。
由图9和图10可见,拉曼光谱的一阶IMF中频率组分比近红外光谱复杂,这是否意味着EMD分解拉曼光谱较近红外光谱更易出现模态混叠现象,即IMF不能严格满足单频率组分的条件,或不同时间尺度的信号被强制分解到同一IMF中,如图11所示为拉曼光谱EMD分解情况。
图11中IMF2和IMF3中均出现了差异很大的特征时间尺度,以及IMF4和IMF5中存在相近特征尺度,图中存在模态混叠现象。经过多组不同种类样品(豆油、水稻叶片、油脂、土壤等)拉曼光谱分解实验表明,拉曼光谱极易出现EMD模态混叠问题[4]。
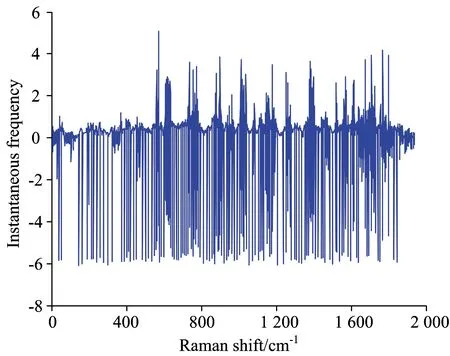
Fig.9 Instantaneous frequency of Raman spectrum IMF1
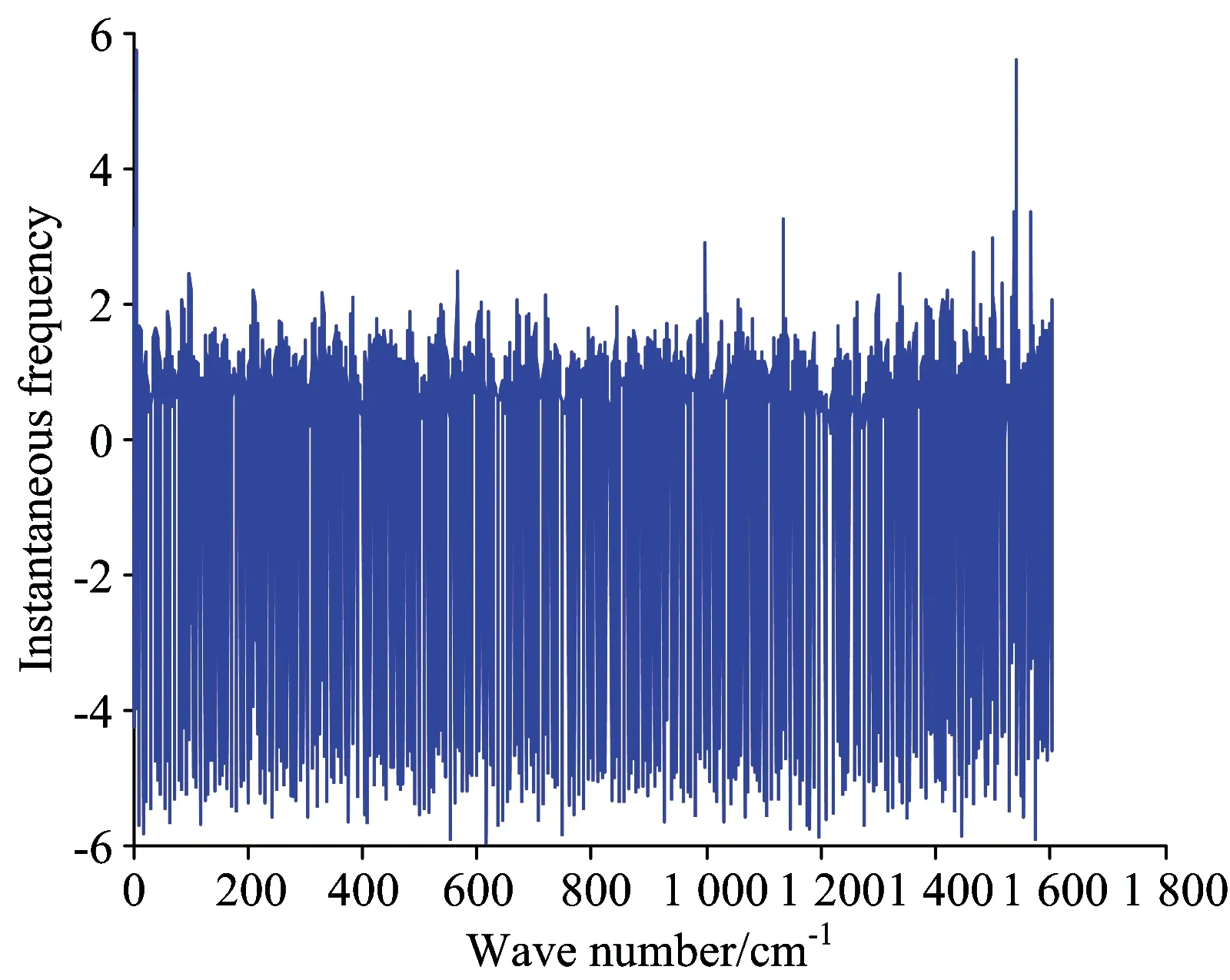
Fig.10 Instantaneous frequency of near infrared spectrum IMF1
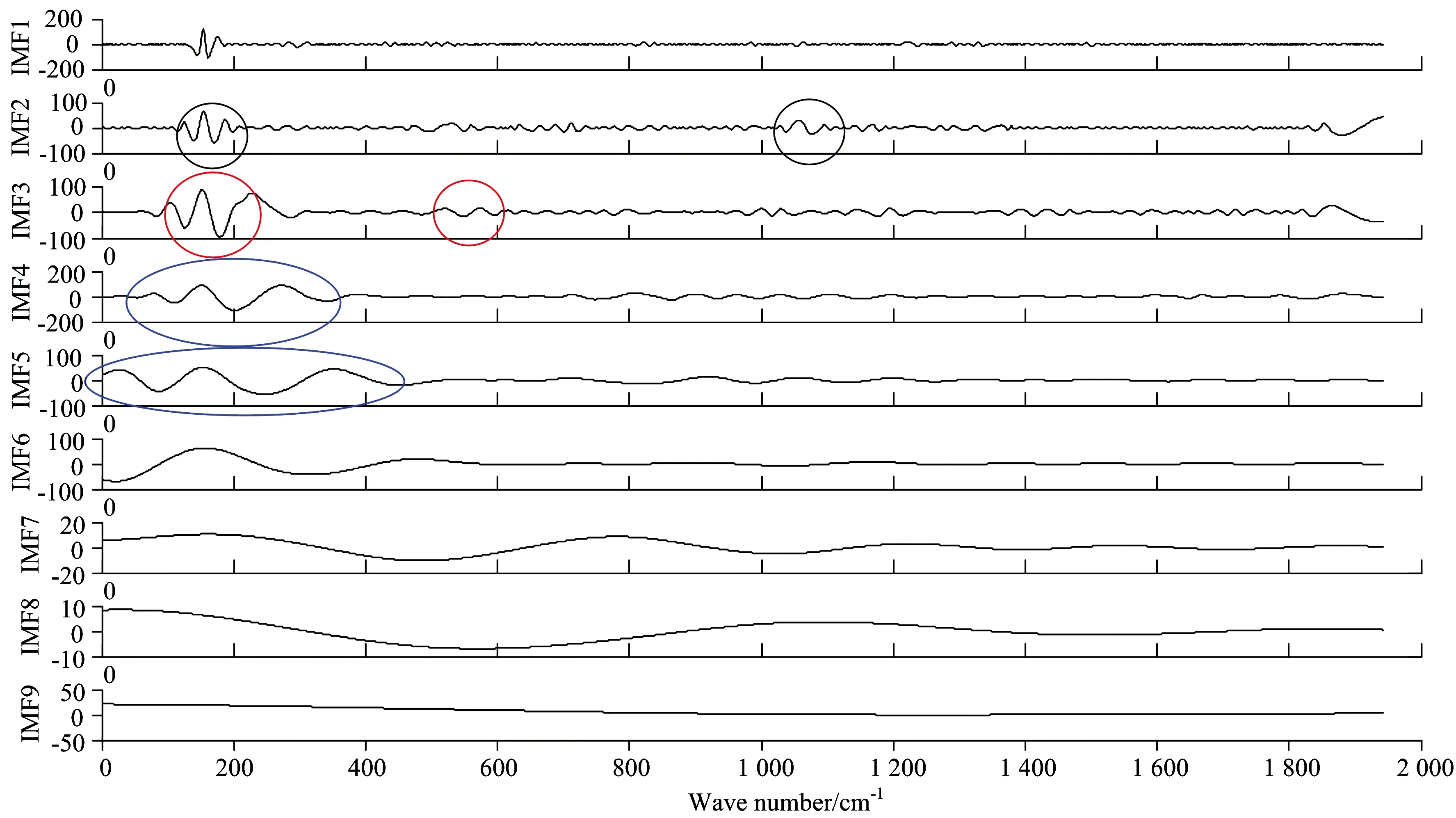
Fig.11 Raman spectrum decomposed by EMD
拉曼光谱的间歇断续使得应该被分解到不同时间尺度的分量被强制分解到同一IMF中,即在信号断续处产生了瞬时频率的畸变,极大影响拉曼光谱瞬时频率的正确表达,为拉曼光谱的进一步时频分析造成了障碍。有两种方法可以解决模态混叠问题: (1)改变EMD筛分规则以克服模态混叠[5-6]; (2)在待分解光谱中加入屏蔽信号,利用两信号之间相互作用解决模态混叠问题,总体均值经验模分解(ensemble empirical mode decomposition,EEMD)就是一个有效的方法[7]。
4 光谱EMD时频分析
综合考虑EMD分解时,拉曼光谱重量分布情况、高频吸附特性和易出现模态混叠现象,以下仅针对近红外光谱作出EMD时频分析。

Fig.12 Reconstructed spectrum signal on proportion and original spectrum signal
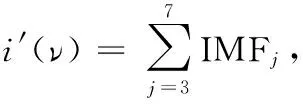
目测两信号拟合良好。只是在光谱开始和结束位置,i′(ν)信号相对光滑,意味着IMF1和IMF2集中承载了原光谱中噪声分量。
可以用以下两个指标度量光谱重构拟合情况。
均方根误差
相关系数
两个指标反映出来重构精度很好,i′(ν)可以表达i(ν)。
下面通过IMF3~IMF7时频分析近红外光谱。首先分析IMF7,一般称之为趋势项,如图13所示,该项总体呈缓慢下降的趋势,这表示随着近红外波长的减小,叶片对光线的吸收呈现递增趋势,而从原始光谱很难得到这种趋势规律。另外,计算IMF7的导数,从趋势项变化情况看出,波数600~1 400(为绘图方便,文中波数从0开始,实际光谱的波数从4 000开始)区间变化加剧,对应图12,光谱的主要透射峰刚好落在该区间。所以缩小分析范围,在600~1 400区间对比辨识非碱胁迫与碱胁迫两类光谱。
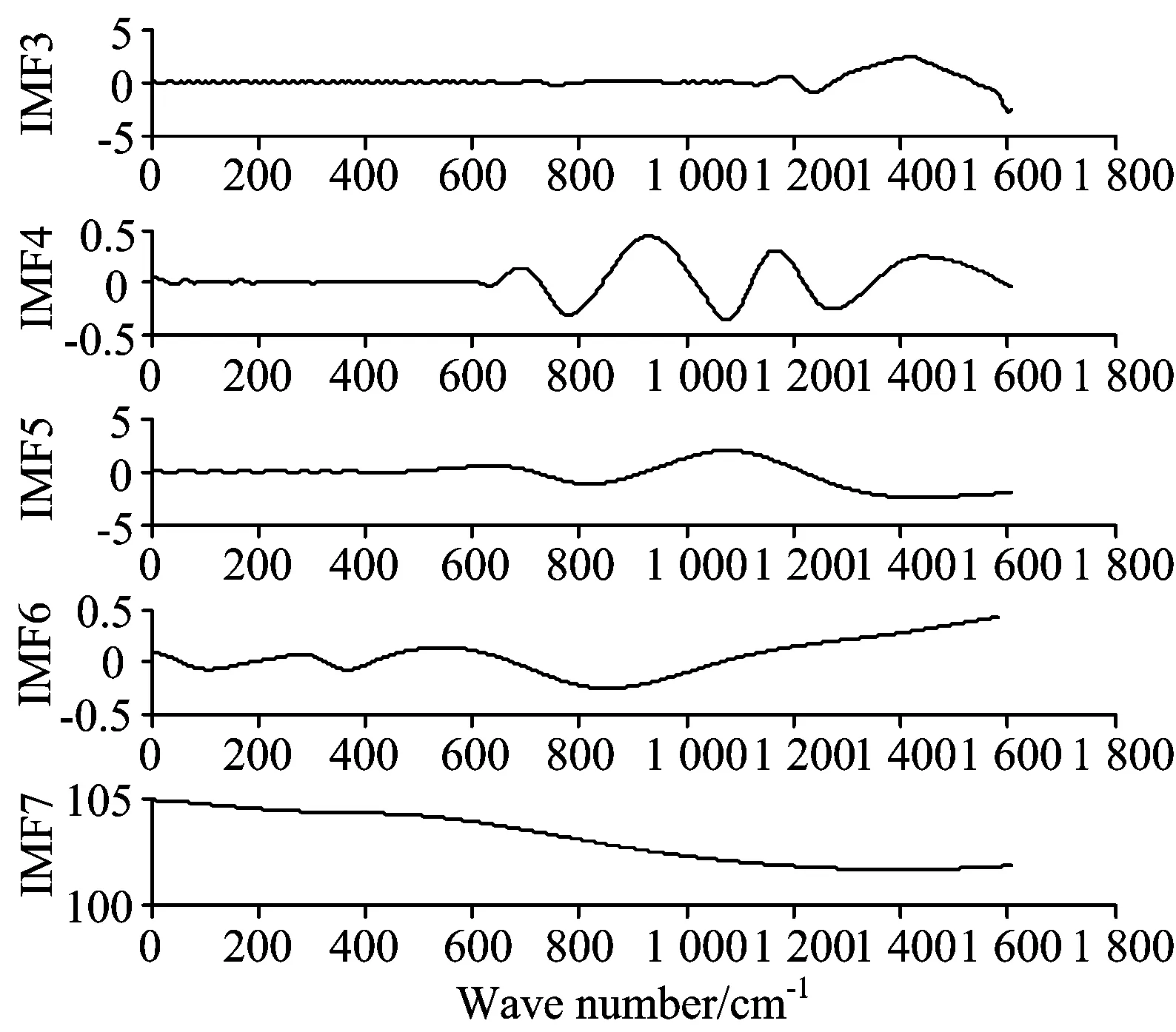
Fig.13 Components of IMF3~IMF7
分量IMF3~IMF6经过Hilbert变换,得到波长频率分谱,将波长频率谱求和,如图14所示。
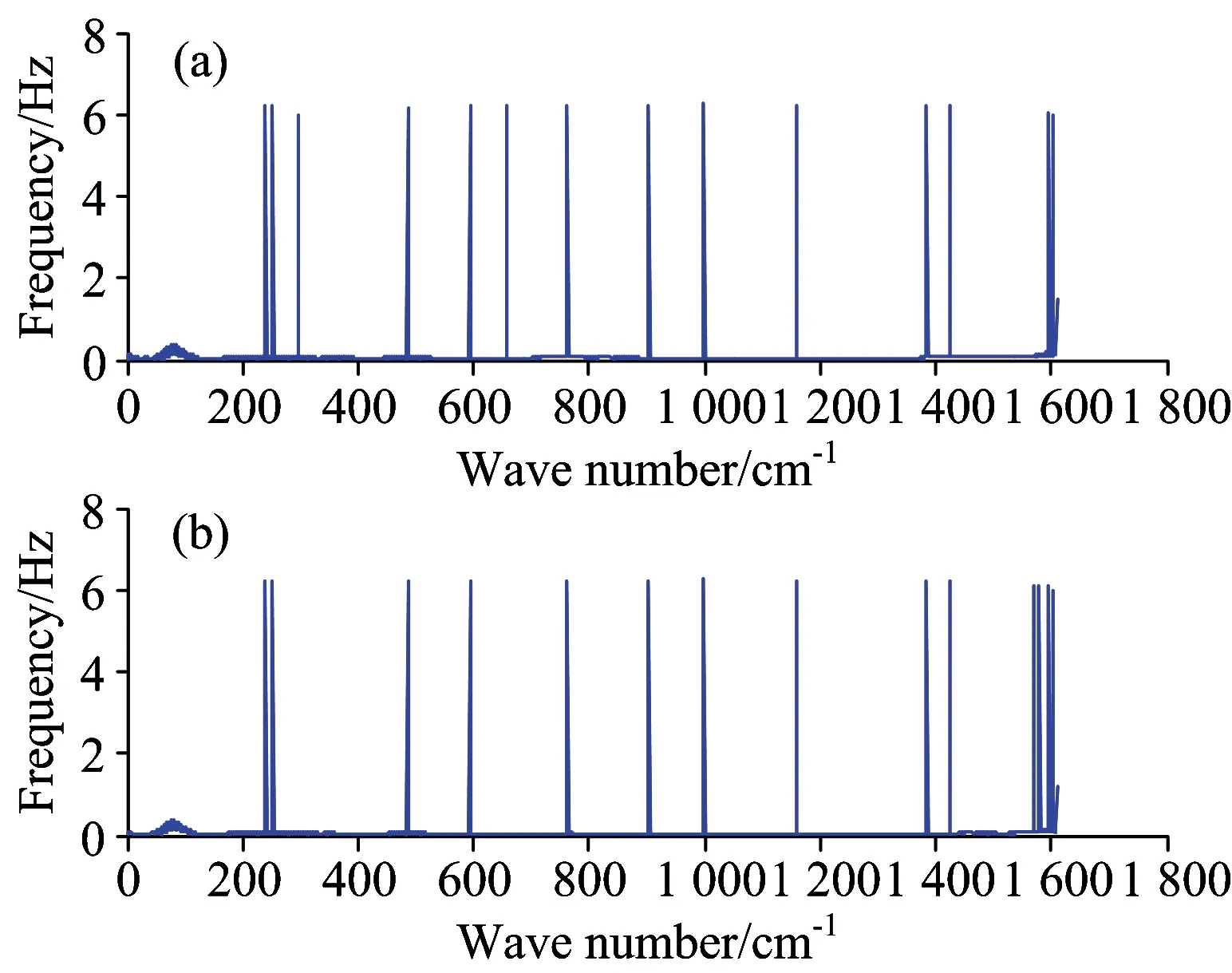
Fig.14 Wavenumber and frequency spectrum by HT
图14(a)为碱胁迫光谱,图14(b)为常规水基培养光谱。对比观察,两幅图谱略有差异,相似度很高。在600~1 400 cm-1波数考察范围内,图14(a)657 cm-1处多出一个特征频率。实验中全部四个浓度碱基样品共100幅光谱,均获得了该特征频率,说明通过657 cm-1特征频率可以辨识出碱胁迫近红外光谱。
5 结 论
(1) EMD分解光谱,近红外和拉曼两种类型光谱存在如下差异:
①一阶IMF能量大,EMD对拉曼光谱幅值影响大,拉曼光谱可视作调幅信号,拉曼光谱具有高频能量吸附特性;
②一阶IMF频率高,EMD对近红外光谱幅值影响不大,近红外光谱可视作调频信号。
(2) EMD分解两类光谱时,拉曼光谱较近红外光谱更容易出现模态混叠现象,无法实现窄带单频分解。
(3) 在近红外光波段,近红外光谱EMD趋势项可以表达随着波长减小,叶绿素吸光度呈现递增趋势;
(4) 通过IMF分量的希尔伯特变换发现,碱胁迫叶片的近红外光谱具有657 cm-1特征频率,而非碱胁迫光谱不具备此特征。
进一步研究方向:
(1) 用EMD、希尔伯特变换对近红外光谱作出时频分析,通过特征频率辨识出碱胁迫和非碱胁迫两类光谱,实现了物质的定性分析。进一步通过研究特征频率与物质分子振动和能级跃迁之间关系,以实现物质的定量分析,期待用特征吸收峰和特征频率双重指标提高近红外检测精度。
(2) 由于拉曼光谱高频能量吸附特性和模态混叠问题,EMD时频分析方法不适合应用到拉曼光谱解析,可以考虑应用EEMD或其他EMD的改进算法,相关问题有待进一步研究。
[1] Huang N E,Zheng Shen,Long S R,et al. Proc. R Soc. Lond A,1998,454: 903.
[2] CAI Jian-hua, WANG Xian-chun, HU Wei-wen(蔡剑华, 王先春, 胡惟文). Transactions of the Chinese Society for Agricultural Machinery(农业机械学报), 2010, 41(9): 182.
[3] CAI Jian-hua, WANG Xian-chun(蔡剑华, 王先春). Acta Optica Sinica(光学学报), 2010, 30(1): 267.
[4] ZHAO Xiao-yu, FANG Yi-ming, WANG Zhi-gang(赵肖宇, 方一鸣, 王志刚). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2013, 33(12): 1.
[5] Huang N E, Wu M, Long S, et al. Proc. R Soc. Lond A, 2003, 459: 2317.
[6] Huang N E, Long S R. Annual Review of Fluid Mechanics, 1999, 31: 417.
[7] Wu Z H,Huang N E. Advances in Adaptive Data Analysis,2009, 1(1): 1.
EMD Time-Frequency Analysis of Raman Spectrum and NIR
ZHAO Xiao-yu1, FANG Yi-ming2, TAN Feng1, TONG Liang3, ZHAI Zhe4
1. College of Information Technology, Heilongjiang Bayi Agricultural University, Daqing 163319, China 2. College of Electrical Engineering, Yanshan University, Qinhuangdao 066004, China 3. Communication and Electronic Engineering Institute, Qiqihar University, Qiqihar 161006, China 4. Forestry Experiment Center of North China, Chinese Academy of Forestry, Beijing 102300, China
This paper analyzes the Raman spectrum and Near Infrared Spectrum (NIR) with time-frequency method. The empirical mode decomposition spectrum becomes intrinsic mode functions, which the proportion calculation reveals the Raman spectral energy is uniform distributed in each component, while the NIR’s low order intrinsic mode functions only undertakes fewer primary spectroscopic effective information. Both the real spectrum and numerical experiments show that the empirical mode decomposition (EMD) regard Raman spectrum as the amplitude-modulated signal, which possessed with high frequency adsorption property; and EMD regards NIR as the frequency-modulated signal, which could be preferably realized high frequency narrow-band demodulation during first-order intrinsic mode functions. The first-order intrinsic mode functions Hilbert transform reveals that during the period of empirical mode decomposes Raman spectrum, modal aliasing happened. Through further analysis of corn leaf’s NIR in time-frequency domain, after EMD, the first and second orders components of low energy are cut off, and reconstruct spectral signal by using the remaining intrinsic mode functions, the root-mean-square error is 1.001 1, and the correlation coefficient is 0.981 3, both of these two indexes indicated higher accuracy in re-construction; the decomposition trend term indicates the absorbency is ascending along with the decreasing to wave length in the near-infrared light wave band; and the Hilbert transform of characteristic modal component displays, 657 cm-1is the specific frequency by the corn leaf stress spectrum, which could be regarded as characteristic frequency for identification.
Time-frequency analysis; Empirical mode decomposition; Hilbert translation; Near infrared spectrum; Raman spectrum
Aug. 7, 2014; accepted Dec. 18, 2014)
2014-08-07,
2014-12-18
黑龙江省科学基金项目(QC2015071, F201329),国家科技支撑项目(2014BAD06B01),黑龙江省教育厅科学技术研究项目(12521378,12541897)资助
赵肖宇,女,1977年生,黑龙江八一农垦大学副教授 e-mail: xy_zhao77@163.com
O657.3
A
10.3964/j.issn.1000-0593(2016)02-0424-06
