爆破拆除楼房时塌落振动的预测

魏晓林， 刘 翼

(广东宏大爆破股份有限公司， 广州 510623)



爆破拆除楼房时塌落振动的预测

魏晓林， 刘 翼

(广东宏大爆破股份有限公司， 广州 510623)

摘要：从十余栋楼房塌落振动综合实测中可见，峰值振速总是由楼房倒塌触地的姿态所决定，即可能发生在后支撑爆破楼房下坐、切口闭合或翻倒触地时，且峰值也不尽相同。由此，在量纲分析中引入重心下落高度，分别建立了楼房下坐、楼房切口闭合冲击和建(构)筑物整体翻倒触地振动的峰值振速经验公式，阐述了相应的楼房、建(构)筑物不同塌落振动原理，并从案例实测振速对数图峰值最大包络线中，摄取公式待定参数Kt、β，由此分别提出对应的峰值振速算法的计算公式，并阐明参数的物理意义和取值。预测地点振速可先按结构选取，高大烟囱、现浇剪力墙(包括前跨现浇剪力墙的框剪结构及13层以上的单向倾倒现浇框剪结构的前方预测点)的塌落峰值振速，选取算法(3)计算峰值振速。框架和其他框剪楼房塌落振动的峰值，可按触地姿态选取算法(1)和算法(2)计算，并选取算法中的较大计算值为预测的峰值振速。由于补充了算法(1)和算法(2)，综合算法正确地反映了形成峰值振速的楼房触地位置和撞地冲击时重心改变的高度，因此振动原理较明确，由此提高了预测塌落振动的针对性和准确性。并结合观测实例进行了公式验证，证明了公式的合理性。

关键词：高大建筑物； 爆破拆除； 触地姿态； 塌落振动； 峰值振速

1引 言

拆除爆破工程实践表明，建筑物拆除时塌落振动往往比爆破振动大。为了估算爆破拆除时塌落的振动强度，从上世纪80年代以来，中科院力学所周家汉〔1〕进行了大量研究，确立了爆破拆除高烟囱和楼房塌落的峰值振速的计算公式。依据这些公式和相应塌落振动机理，对十余栋楼房和烟囱的塌落振动进行了测量，并结合摄像、应变电测和塌落姿态动力学分析对塌落振动进行了预测。发现楼房的塌落振动与钢筋混凝土烟囱的塌落振动在原理上有所区别，测值的规律上也有差异。

2塌落振动原理及计算

周家汉〔1〕和费鸿禄〔2〕研究以及大量建(构)筑物的塌落实测和量纲分析显示，建筑物拆除的塌落振动与重力势能mgh有关，即与下落物件的质量m和触地速度平方v2有关(v2=2gh)，h为重心下落的高度，并随振动传播的距离R的增加而衰减，即塌落振动的衰减公式为：

vt=K[R/(2mgh/σ)1/3]β′

(1)

v2也可以与H成正比，由此，对高H的烟囱类高大建(构)筑物塌落振动的公式〔3〕，改写为：

vt=Kt[R/(mgH/σ)1/3]β′

(2)

式中：β′为负衰减指数；Kt、K为与波传播有关的场地系数；σ为地面或构件的介质破坏强度，一般取10MPa。式(2)法称为振动预测法(3)。

实践证明，对烟囱类高大建筑(构)物，振速的最大值出现在烟囱单向整体倾倒触地时。分析高210m烟囱单向倾倒爆破拆除塌落振动的波形〔4〕(图1)。

图1　210m烟囱爆破倾倒塌落振动波形Fig. 1　Vibration waveform of 210m chimney toppling collapse

图1所示的振动波时程曲线有先后到达的4个波动信号，即0s时的爆破，0.7s的筒壁下坐，3.6s～4.5s的切口闭合，最后17.0s～18.1s，是烟囱整体触地塌落振动波，其作用时间长，频率低，幅值也最大。但是爆破拆除现浇钢筋混凝土楼房时，却往往并非如此，单向倾倒的楼房，在下坐或切口闭合时，往往比整体倒地的振动还大。如中山古镇11层V形框剪楼单向倾倒爆破拆除塌落振动波形(图2)。

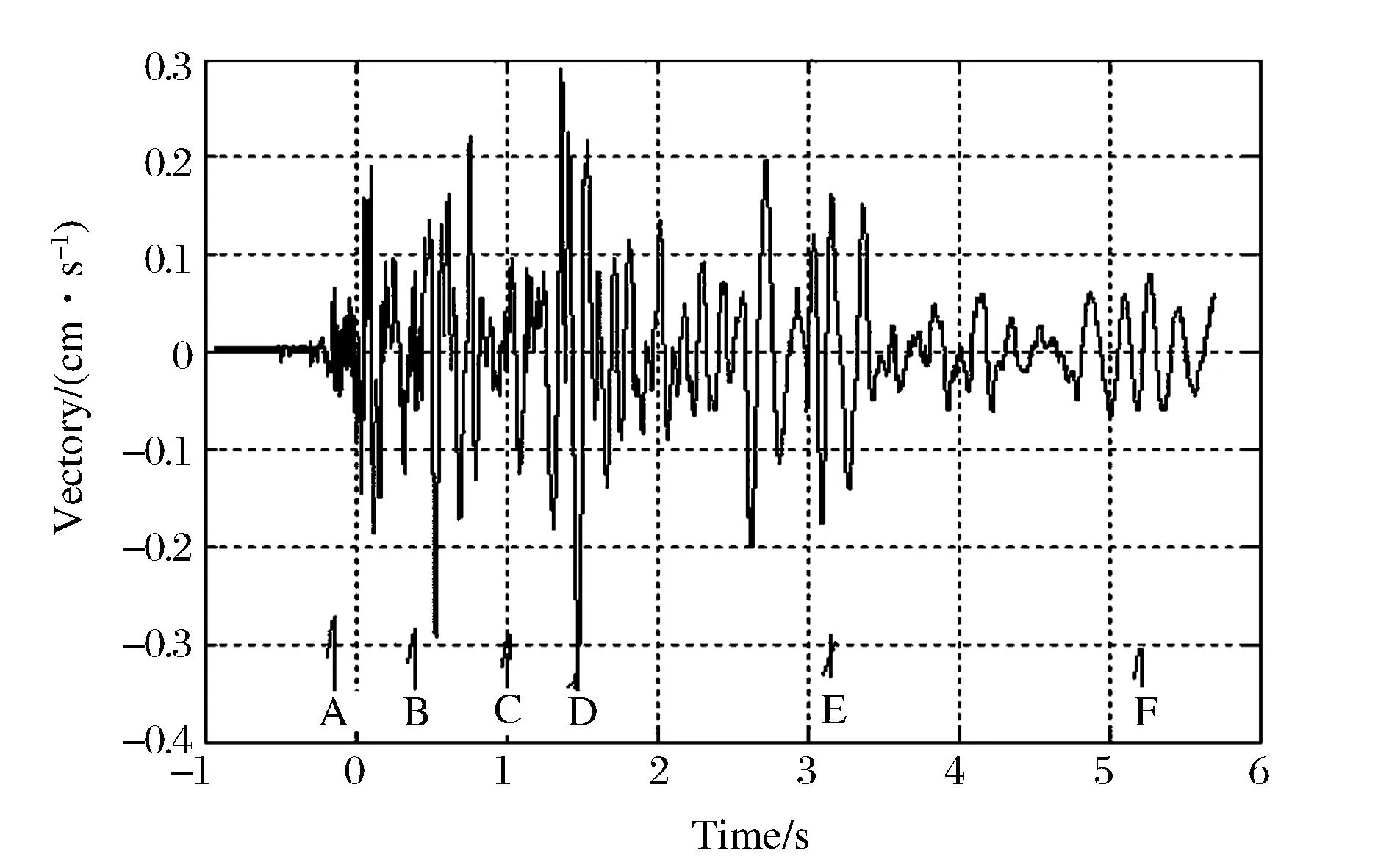
A-前、中间中柱爆破 Front and the middle columns blasting；B -边前、中柱爆破 Edge front and middle columns blasting;C,D-边中、后柱爆破并下坐 Side columns and rear columns blasting and sitting down; E-切口闭合 Incision closed；F-楼房翻倒触地Building toppling on ground图2　某11层V形框剪楼单向倾倒爆破拆除塌落振动波形Fig.2　Vibration waveform of 11-storey V shape frame shear building demolition by blasting

图2振动波时程曲线有先后到达的5个波动信号，即-0.25s～0s时前柱和楼中间中柱爆破的A波；0.5s中柱和楼边前柱起爆的B波；1.0s～1.5s后柱和楼边中柱起爆到下坐撞地的C，D波，其波形为主峰D，幅值为0.3244cm/s；而3.2s切口闭合时，E振波为次峰值0.18cm/s；然后振动波幅值减少，5.2s楼房整体翻倒触地的F波，振波幅值再次增大，但幅值仅为0.075cm/s。如省委大院10#楼侧面C1测点的振动波形(图3)。

A-前柱爆破 Front columns blasting；B-中、后柱爆破并下坐 Middle columns and rear columns blasting and sitting down；C-切口闭合，而后各层依次层间侧移触地 The Incision closed图3　某框架楼房爆破拆除倾倒层间侧移塌落侧向C1点振动波形Fig.3　The vibration waveform of 7-storey building toppling demolished by blasting

与图2相似，图3所示振动波时程曲线有先后到达的4个波动信号，即-0.1s～0.1s时前柱爆破的A波；0.2s中柱和后柱起爆并下坐的B波，其波形为主峰0.32cm/s； 1.9s切口触地的C波，为次峰值0.26cm/s；而2.7s为层间侧移〔5〕底层的上一层闭合时的振波，振速低峰值减少到0.1cm/s，以后振速也更小。10幢楼房爆破拆除振动波形特征如表1所示。

表1　爆破拆除楼房振动波特征及其时刻

从表1中可见，其中6幢楼房振动主峰在后柱爆破下坐时，3幢楼房塌落振动主峰在切口闭合时，1幢楼房振动主峰在楼房翻倒触地时，且楼房翻倒触地中心距前方测点最近。由此可见，现浇钢筋混凝土楼房塌落振动主峰幅值与楼房的结构、爆破拆除的方式和触地的姿态等因素有关，而触地姿态即是楼房下坐、切口闭合冲击或翻倒触地。

对8层以下楼房，后柱的炸高多为0.9m～1.2m，后柱爆破时楼房下坐，较多楼房振动达到峰值，如表2所示。

表2　楼房下坐峰值振速预测方法比较

注：预测(1)的vt=Kt[(mg2he/σ)1/3/R]β。式中he为下坐高，m;R为爆破后支撑中点的距离，m； β=1.16；，例1～例7.1Kt=5.4，例8.1和8.2Kt=7.8；预测(3)为文献〔1〕的方法，Kt=3.37；β=1.16；M为振速最大值。表中备注(预算2)为切口闭合振速预测算法(2)。

从表2中例7.1也可见，珠海江村20层楼房应变电测，也证明下坐时后柱应变片应力突变而同时塌落振速也最大。文献〔2〕也得出毫秒延时爆破拆除建筑物时其后坐触地产生的振速更大。随着楼层增高，其宽度也增大，爆破切口也跟随加高，楼房触地冲击势能将加大，因此8层以上楼房切口闭合时，多数楼房振动达到峰值。14层以上的多切口拆除楼房，被切口分割的房体将分别触地冲击，下体切口闭合时，振动达到峰值。倒塌的楼房经后柱爆破下坐，切口闭合冲击，楼房的整体结构已经破坏，各构件带缝钢筋连接，非完全离散〔5〕，乃至完全离散，翻倒触地时，撞地力分散，因此振动幅值较小。但是，单向倾倒的20层以上现浇剪力墙楼房，部份构件体下落高度大，触地势能还高，仍可能形成振速主峰。由此可见，现浇钢筋混凝土楼房塌落振动的峰值振速时刻将依次可能出现在中、后支撑爆破下坐，切口闭合和翻倒触地时，且振动原理有所差异，峰值、次峰也有相互影响。

因此，峰值振速的计算分别对应下坐、切口闭合和整体翻倒三种算法。数幢楼房下坐的峰值振速见表2。切口闭合的的峰值振速见表3，M代表楼房塌落振动速度最大值，并将实测PPV振速绘入图中。

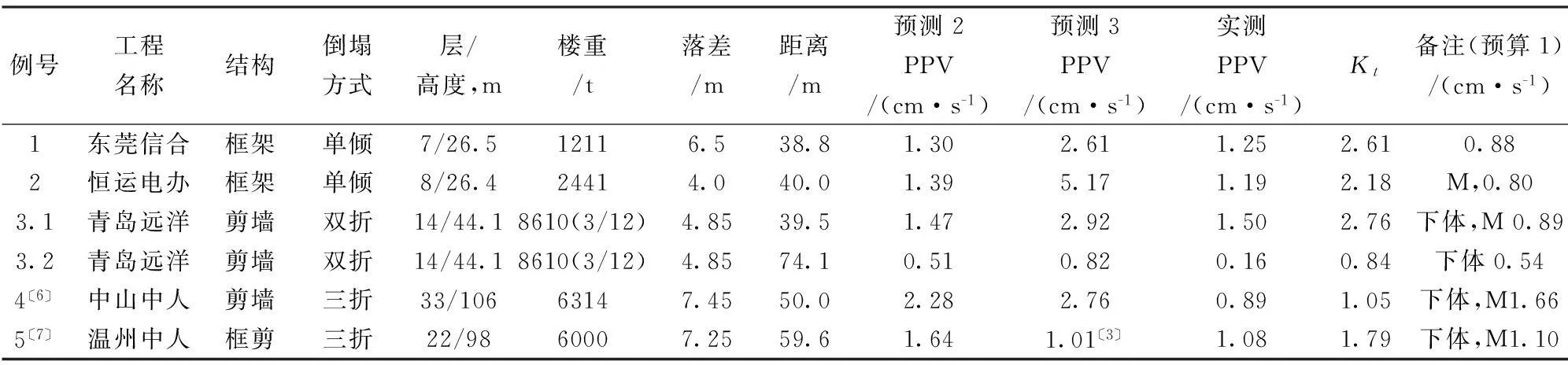
表3　楼房切口闭合峰值振速预测方法比较

注：预测(2)的vt=Kt[(mgH/σ)1/3/R]β。H为切口高，m，落差为H/2;R为切口闭合前沿中点距测点距离，m；Kt=2.7；β=1.16。预测(3)为文献〔1〕的方法，Kt=3.37；β=1.16；M为全振动最大值。表中备注(预算1)为下坐振速预测算法(1)。

首先，根据式(1)，作楼房下坐的峰值振速对数图(图4)，R′=R/(2mghe/σ)1/3，he为爆破引起下坐的支柱炸高，m。

A线Kt=5.4，β′=-1.66;B线Kt=7.8，β′=-1.66图中数字为表2例号,7.1～7.6为例7的不同测点图4　下坐峰值振速测量值Fig. 4　PPV measured during sitting down

另外，根据式(1)改写，作楼房切口闭合峰值振速对数图(图5)，R′=R/(mgH/σ)1/3，H为切口高，m。

D线Kt=2. 7, β′=-1.66;C线Kt=3.37;β′=-1.66图中数字为表3例号图5　切口闭合峰值振速测量值Fig.5　PPV measured when incision closed

由此可以得到楼房塌落振动补充的(1)、(2)算法，即综合以上图、表可见，若预测塌落振动的公式仍采用式(2)，将楼房下坐振动作为预测法(1)，则H=2he，R为爆破引起下坐支撑在地面连线的中点到预测振动目标点的距离，m。而Kt=K和β=-β′，可从图4得到，其中倾倒下坐振动峰值Kt=5.4，塌落下坐Kt=7.8～9.1，β=1.66。而当切口闭合时，作为切口闭合的峰值振速的预测法(2)，H取切口高；R为切口前缘闭合触地中心距预测峰值振速点距离，m。而Kt=K和β=-β′也可从5幢楼房的切口闭合峰值振速对数(图5)中获得，楼房的切口闭合峰值振动的Kt=2.7，β=1.66。切口闭合的Kt值小于下坐振动的Kt，因为钢筋混凝土楼房下坐撞地后，楼房已有所破坏，刚度降低，重心单位下落m的撞地力有所减小而形成。而振动传播的衰减系数β，在图4和图5中从多幢楼房测值与文献〔1〕比较均显得较小，但从珠海江村单幢楼房塌落的振速看，β仍然较大，因而仍按文献〔1〕中β=1.66计算。此外，楼房整体翻倒触地峰值振速计算仍作为原算法(3)，仍按原式(2)，文献〔1〕中Kt取3.37～4.09，H为楼房(或下体)和烟囱的高度，R为预测地目标点与塌落中心距离，m，β=-β′，β=1.66。由此，将文献〔1〕中楼房塌落振动的峰值振速计算进行了完善，补充了算法(1)和算法(2)，形成了新的楼房塌落振动预测流程和方法。

从上式的分析可见，算法(1)和算法(2)正确反映了形成峰值振速的楼房触地位置和撞地冲击时重心改变的高度，因此将改善式(2)文献〔1〕仅一个算法(3)的预测值，而更接近实测PPV峰值。在表2和表3比较中可见，算法(1)和算法(2)的预测值绝大多数都比文献〔1〕的算法(3)的预测值小，且其中较大者都大于实测峰值振速，因此又是安全的。表2的例3后跨梁端弱，中、后柱下坐两层，其Kt=9.1，略超算法(1)的Kt=7.8，但算法(2)的预测值仍大于实测值；表2的例8.1和8.2，也是属下坐两层以上的整体塌落，当楼房底层后柱炸高超过1.6m时，就易于发生整体塌落〔5〕。另外，表2的例6算法(1)的预测值大于算法(3)是可能的，在靠近楼房两侧和后方25m内，预测值会大于算法(3)，但是正常的。再以算法(3)的1/2改进值预测，其部分预测值接近实测值及其逆算的Kt，比较准确。但表2中的例2、例4.1、例4.2和例7.1的框架、前跨框架的框剪结构塌落振速的计算值比实测峰值振速高出5.2～9.59倍。由此可见，算法(2)还是比原公式(2)的文献〔1〕仅一个算法(3)及其预测值的1/2预测，较为准确，且振动原理正确。对于单向倾倒现浇全剪力墙楼房以及前跨有剪力墙的框剪结构，因整体倾倒触地的塌落振动峰值有可能大，且实测案例较少，难以肯定用算法(1)和算法(2)，仍按算法(3)预测。

综上所述，当爆破拆除楼房振动预测时，其新流程是框架和框剪楼房按塌落振动补充的算法(1)和算法(2)所对应的条件，分别计算PPV振速，再取其最大值，为目标点预测的峰值振速。而烟囱、现浇全剪力墙楼房和前跨有剪力墙的框剪结构及13层以上的单向倾倒现浇框剪结构的前方预测点仍按原算法(3)预测。

3应用实例

现以框架结构的恒运电厂8层办公楼单向倾倒爆破拆除为例〔8〕，预测前方40m目标点的峰值振速。当切口闭合时，以算法(2)计算，取楼房切口高H=8m，质量m=2 441t，R=40m, β=1.66，Kt=2.7，计算峰值振速v2=1.39cm/s;而当楼房后柱下坐时，按算法(1)计算，取后柱炸高he=0.9m，m=2 441t，R=51.6m，β=1.66，Kt=5.4，计算峰值振速v1=0.8cm/s；而算法(3)不适合框架结构，不进行计算。因v2>v1，故预测计算峰值vt=v2=1.39cm/s，实测值为1.19cm/s，小于预测值，因此预测值是安全的。假如采用算法(3)预测，楼高H=26.4m, m=2 441t，R=30.8m, β=1.66，Kt=3.37，计算峰值振速v3=5.17cm/s；v3>v1，v1也小于v3/2和v3/3。可见算法(3)不适合框架结构计算，框架结构塌落振波峰值振速可按算法(1)和算法(2)预测并取其较大者。

4结 语

(1)建(构)筑物爆破拆除的塌落振动的峰值振速，可能发生在中、后支撑爆破楼房下坐、切口闭合或翻倒触地时，中科院力学所周家汉的预测目标点峰值振速vt=Kt[(mgH/σ)1/3/R]β的公式是合适的，其中参数取值除了应考虑建筑结构、拆除方式、土岩性质等因素外，还应考虑倒塌姿态。先按结构选取高大烟囱、现浇剪力墙(包括前跨现浇剪力墙的框剪结构，13层以上的单向倾倒现浇框剪结构的前方预测点)塌落振动的峰值振速，选取算法(3)计算峰值振速。框架和其他框剪楼房塌落振动的峰值振速可按触地姿态〔5〕，选取算法(1)和算法(2)计算，并选取算法中的较大计算值为预测的峰值振速。式中m为楼房(或下体)、烟囱的质量，103kg，σ为地面介质的破坏强度，一般取10MPa。由于补充了算法(1)和算法(2)，综合算法正确地反映了形成振波峰值振速的楼房触地位置和撞地冲击时重心改变的高度，因此振动原理较明确，提高了预测塌落振动的针对性和准确性。

(2)补充的算法(1)是楼房后支撑爆破的峰值振速，发生在楼房下坐时。楼房倾倒兼塌落Kt=5.4～6.2，整栋楼房塌落下坐(或首次下坐底2层以上)Kt=7.8～9.2，H=2he，he为爆破引起下坐的后支撑炸高，R为爆破引起下坐支撑在地面连线的中点到预测振动目标点的距离，m；β=1.66～1.8。

(3)补充的算法(2)是框架和框剪楼房切口闭合时的峰值振速，发生在切口闭合时，Kt=2.7～3.08，β=1.66～1.8，H为下切口高，m，R为下切口前缘闭合触地中心与预测峰值振速点距离，m。

(4)原算法(3)为高大烟囱、现浇剪力墙(包括前跨现浇剪力墙的框剪结构)，倾斜翻倒触地的峰值振速，发生在烟囱和楼房(或下体)翻倒整体触地时。按中科院力学所周家汉的研究文献〔1〕、〔3〕，Kt取3.37～4.09，H为楼房(或下体)和烟囱的高度，R为预测地目标点与翻倒塌落中心距离，m， β=1.66～1.8。

(5)若地面采取挖沟槽等减振措施，Kt值还会降低1/2以上〔3〕。楼房塌落振动的危害多发生在邻近侧面和近距的后方保护目标，因此为保护该目标，减振沟可挖在塌落楼房的切口闭合侧前后和不会加大下坐的后方。此外，降低爆破后支撑炸高，也可减小下坐振动。

参考文献(References)：

〔1〕 周家汉，陈善良，杨业敏，等. 爆破拆除建筑物时震动安全距离的确定[M]//冯叔瑜. 工程爆破文集(第三辑). 北京：冶金工业出版社,1988:112-119.

ZHOU Jia-han, CHEN Shan-liang, YANG Ye-min, et al. Determine the chocking safety distances in blasting demolition of building[M]//FENG Shu-yu. Engineering Blasting Corpus (3rd cir.). Beijing: Metallurgical Industry Press,1988:112-119.

〔2〕 费鸿禄，张龙飞，杨智广. 拆除爆破塌落振动频率预测及其回归分析[J]. 爆破,2014,31(3):28-31,95.

FEI Hong-lu, ZHANG Long-fei, YANG Zhi-guang. Forecast of collapsing vibrating frequency of demolition blasting and its regression analysis[J]. Blasting,2014,31(3):28-31,95.

〔3〕 周家汉. 爆破拆除塌落振动速度计算公式的讨论[J]. 工程爆破,2009,15(1):1-4,40.

ZHOU Jia-han. Discussion on calculation formula of collapsing vibration velocity caused by blasting demolition[J]. Engineering Blasting, 2009,15(1):1-4,40.

〔4〕 刘翼，魏晓林，李战军. 210m烟囱爆破拆除振动监测及分析[M]//汪旭光. 中国爆破新技术.北京：冶金工业出版社,2012:964-971.

LIU Yi, WEI Xiao-Lin, LI Zhan-jun. Measuring vibration and analysis of chimney high 210m demolished by blasting[M]// WANG Xu-guang. New Technology of Blasting Engineering in China. Beijing: Metallurgical Industry Press,2012:964-971.

〔5〕 魏晓林. 建筑物倒塌动力学(多体-离散体动力学)及其爆破拆除控制技术[M]. 广州：中山大学出版社，2011.

WEI Xiao-Lin. Dynamics used on building demolition by blasting & controlled theory [M]. Guangzhou: Zhong Shan University Press, 2011.

〔6〕 朱朝祥，崔允武，曲广建，等. 剪力墙结构高层楼房爆破拆除技术[J]. 工程爆破，2010,16(4):55-57,40.

ZHU Chao-xiang, CUI Yun-wu, QU Guang-jian, et al. Blasting demolition technique of high building with share wall structure[J] Engineering Blasting,2010,16(4):55-57,40.

〔7〕 曲广建，崔允武，吴岩，等. 温州93m高结构不对称楼房拆除爆破[M]// 汪旭光. 中国典型爆破工程与技术. 北京：冶金工业出版社，2006:615-620.

QU Guang-jian, CUI Yun-wu, WU Yan, et al. The asymmetry structure building high 93m demolished by blasting in Wenzhou[M]//WANG Xu-guang.Chinese typical blasting engineering and technology. Beijing: Metallurgical Industry Press,2006: 615-620.

Prediction of collapse vibration of building demolished by blasting

WEI Xiao-lin, LIU Yi

(Guangdong Hongda Blasting Co., Ltd., Guangzhou 510623, China)

ABSTRACT：More than ten buildings collapse vibration were comprehensively measured, and peak vibration velocity was always determined by building collapse touchdown attitude, it′s likely to occur in rear support sitting down by blasting, incision closure or toppling on ground, and the peak values were not same. Therefore, falling height of the center of gravity was introduced in dimensional analysis, the empirical formula of the peak value of vibration speed of buildings sitting down, incision closure shock and building (structure) overturned wholly on ground were respectively established. Different collapse vibration principle were correspondently described. Formula parameters Kt and β were taken out from the peak envelope line of case in measured velocity logarithmic graph. Formulas respectively corresponding to peak velocity algorithms were proposed, and physical meaning of parameters and values were explained. According to the structure selected,high chimneys, cast-in-place shear wall (including the former cross cast-in-place shear wall ahead of frame and front site of cast-in-situ frame shear wall structure more than 13 storeys), prediction collapse vibration peak velocity was calculated by algorithm (3). Frame and other shear wall frame buildings collapse vibration peak was calculated by touchdown attitude to select algorithm (1) and (2), the vibration velocity greater was selected for the prediction vibration value. Algorithm(1) and (2) were supplemented, integrated new algorithm correctly reflected touchdown position of formation of vibration wave peak of building and the changed height of the center of gravity of impact hit on ground, so the principle of vibration was more explicit and the pertinence and accuracy of collapse vibration predicted would be improved. The observed examples were listed and the rationality of the formulars were proved.

KEY WORDS:High and larger building; Blasting demolition; Touchdown posture; Collapse vibration; Peak vibration velocity

文章编号：1006-7051(2016)02-0013-06

收稿日期：2015-10-08

作者简介：魏晓林(1940-)，男，教授级高级工程师，从事工程爆破和矿山安全研究。E-mail: wxl_40@163.com

中图分类号：TD235.3

文献标识码：A

doi：10.3969/j.issn.1006-7051.2016.02.003