固定辙叉轮轨接触关系算法研究及软件开发
2016-06-15赵卫华
赵卫华,王 平,黄 惟
(1.福建工程学院土木工程学院,福州 350118; 2.福建省土木工程新技术与信息化重点实验室,福州 350118; 3.西南交通大学高速铁路线路工程教育部重点实验室,成都 610031)
固定辙叉轮轨接触关系算法研究及软件开发
赵卫华1,2,王平3,黄惟1,2
(1.福建工程学院土木工程学院,福州350118; 2.福建省土木工程新技术与信息化重点实验室,福州350118; 3.西南交通大学高速铁路线路工程教育部重点实验室,成都610031)
摘要:基于轮轨接触理论,考虑固定辙叉复杂的轨头廓形变化及轨距线不连续,提出能够准确计算固定辙叉轮轨接触参数的算法并编制相应计算软件。通过现场试验,对LM型踏面通过60 kg/m钢轨12号合金钢组合辙叉时的轮轨接触点位置(包括沿辙叉纵向和各关键断面)进行测量,并与软件计算结果对比分析;采用该算法分析60 kg/m钢轨12号提速道岔整铸辙叉翼轨加高这一优化设计对轮轨接触参数的影响。结果表明,沿辙叉走行方向和辙叉各关键断面,实测值与软件计算的轮轨接触点变化规律基本一致;对翼轨适当加高可以优化轮轨接触关系,降低辙叉竖向不平顺,验证了该算法的正确性和软件的可行性,便于准确、高效地对固定辙叉区轮轨关系进行优化设计。
关键词:铁路道岔;固定辙叉;轮轨接触关系;软件开发;不平顺;优化设计
固定辙叉是铁路道岔中限制列车速度的关键部件之一,由于固定辙叉存在有害空间,且辙叉咽喉区轮载过渡区段翼轨和心轨廓形连续不规则变化,造成辙叉区轮轨接触关系复杂,结构不平顺较可动心辙叉大,严重限制列车速度的提高。各国学者对轮轨接触关系的研究都非常重视,对区间线路轮轨接触关系问题提出了多种计算模型和方法[1-6],近几年来对复杂的道岔区轮轨接触关系及结构优化设计的研究也越来越多[7-12],文献[7]提出了一种计算道岔转辙器部分轮轨两点接触的数值方法,并分析了车轮踏面廓形对轮轨两点接触的影响;文献[8]建立了可动心道岔转辙器和辙叉区轮轨接触的算法,并进一步确定了轮轨力在基本轨与尖轨、翼轨与心轨之间的转移和分配特性,文献[10-12]从心轨轨顶高度、翼轨和心轨廓形、查照间隔等结构设计参数对固定辙叉进行了优化设计。
针对固定辙叉不规则的钢轨廓形变化,基于迹线法[1]提出了固定辙叉区轮轨接触关系算法,并开发了计算软件。以60 kg/m钢轨12号合金钢组合辙叉与LM型车轮踏面相匹配,从现场试验和软件计算两个方面获得轮轨接触点变化规律并进行对比分析,采用该算法对高锰钢整铸辙叉翼轨加高进行优化设计,进一步验证了该算法的可行性。
1固定辙叉区轮轨接触关系算法基本原理
固定辙叉区轨头截面廓形的不规则变化及有害空间的存在使其轮轨接触关系较区间线路复杂,因此实际的辙叉区轨头截面廓形对分析轮轨接触关系是十分必要的。
1.1轮轨廓形数据生成
借助绘图软件从标准设计图中提取轮轨横截面廓形,并将车轮踏面和钢轨轨头截面离散为一系列坐标点,利用式(1)所示的三次样条函数,将这些离散的坐标点拟合成一条光滑的曲线用以代表轮轨外形。
(1)
式中,S(x)为通过所有坐标点(xk,yk)(k=0,1,2,…,n)的一条光滑曲线;Mk=S″(xk);x为区间[xk-1,xk]上的任意点;lk=xk-xk-1。
由于固定辙叉心轨、翼轨轨头相分离,为方便数据拟合和截面插值,将同一横截面处的心轨和翼轨坐标点合并为一个廓形数据文件参与求解。考虑到轮缘槽对轮轨接触关系的影响,以标准60 kg/m钢轨轨顶中心向下30 mm处用直线连接对应的心轨和翼轨断面,并保证二者相对位置符合轮缘槽标准宽度。图1为辙叉两个关键断面心轨和翼轨拟合后得到的位置关系。
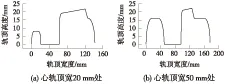
图1 心轨和翼轨拟合的钢轨断面
标准辙叉设计图只提供辙叉关键部位的钢轨截面,为了获得沿线路方向任意钢轨截面廓形,可以由两侧相邻的关键截面线性插值生成,如图2所示。
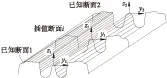
图2 固定辙叉任意截面外形插值
1.2固定辙叉轮轨接触关系
固定辙叉心轨顶面轮廓随车轮的移动逐渐加宽和升高,翼轨顶面轮廓及方向也逐渐改变。从图3所示的整铸式固定辙叉可见,当车轮沿翼轨向叉心方向滚动时,随着翼轨偏离辙叉中心线,固定辙叉有害空间逐渐加宽,轮轨接触点向远离轮缘侧移动,直至车轮与心轨接触时,轮轨接触点发生转移,即向轮缘侧移动。

图3 固定辙叉轮轨接触迹线
该固定辙叉心轨、翼轨在关键截面的相对位置如图4所示,在心轨顶宽20 mm至50 mm范围内为轮载过渡段,心轨高度也逐渐变化,从而实现轮载在翼轨与心轨间的平顺过渡,轮轨接触情况复杂。

图4 心轨顶宽与顶高变化关系(单位:mm)
1.3接触参数求解
假设轮轨间为刚性接触,车轮踏面与心轨、翼轨同时接触的可能性极小,所以在同一辙叉横截面上一侧钢轨只考虑单点接触。依据上述方法求得车轮踏面和关键断面钢轨拟合曲线后,利用样条函数求得轮轨任意点坐标,进而采用迹线法求出轮轨接触点的位置,固定辙叉区轮对侧滚角的确定与区间线路相同[6]。对于踏面等效锥度和结构不平顺的计算,则由于固定辙叉特殊的结构形式而与区间线路不同。
(1)踏面等效锥度
由于固定辙叉存在轨迹线中断的有害空间,当轮对无横移通过辙叉时,左右车轮的滚动半径也有可能不相等,分别为rl0和rr0。依据区间线路车轮的实际滚动圆半径求解公式[6],可得固定辙叉区轮对中心向右横移yw时的左右车轮实际滚动圆半径为
(2)
式中,rl0和rr0分别为轮对没有发生横移时左右车轮的实际滚动圆半径;rl和rr分别为轮对发生横移时左右车轮的实际滚动圆半径;λe为踏面等效锥度。
依据式(2),可以导出固定辙叉区踏面等效锥度与车轮滚动圆半径及轮对横移量的关系
(3)
(2)结构不平顺
不考虑固定辙叉的几何形状、空间位置及尺寸相对其正常状态的偏差,即不存在轨道几何不平顺时,由于翼轨、心轨截面宽度及高度不断变化,接触点的位置随截面位置的不同而改变,于是产生了轮轨接触点在横向及竖向的变化,称之为辙叉的“结构不平顺”,它是引起列车振动、轮轨动作用力及轮对蛇形运动的根源。若不平顺过大,则会使轮轨动作用力在心轨薄弱断面处骤增,或造成轮对蛇形运动时产生爬轨的危险。
根据列车过岔时产生的激扰作用方向,结构不平顺可分为横向和竖向不平顺。计算方法如图5所示。
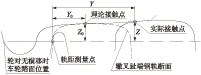
图5 结构不平顺求解示意
以轨距测量点为坐标原点,设无轮对横移时辙叉趾端轮轨接触点距轨距测量点的横向距离为Y0,竖向距离为Z0,该接触点称为理论接触点,则在轮对在辙叉其他部位任意可能的实际接触点在该坐标系中的位置可表示为(Y,Z),所对应的辙叉横向不平顺Yl和竖向不平顺Zv分别为
(4)
式(4)反映了横向不平顺以实际接触点至坐标原点的横向距离较理论接触点远为正,竖向不平顺也是以实际接触点至坐标原点的竖向距离较理论接触点远为正;反之则为负。
2轮轨接触关系算法的软件实现
固定辙叉区轮轨接触点的位置会受到车轮踏面廓形、轮缘廓形、心轨及翼轨轨头廓形的影响。在车轮不同的横向位移的条件下,左右轮轨之间的接触点有不同位置,于是轮轨之间的接触参数也相应出现变化,提出了固定辙叉区轮轨关系算法,并编制了相应的计算软件,该算法流程如图6所示。
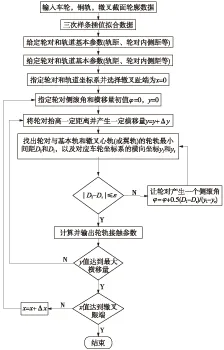
图6 固定辙叉轮轨接触关系算法流程
该计算软件不仅可以生成固定辙叉的结构不平顺,较为准确地反映辙叉系统复杂的轮轨接触关系,得到比较真实的轮轨接触参数,而且可以对固定辙叉关键设计参数,如轮缘槽、轨底坡、轨距等进行优化,设计不同方案进行结构优化。其具体步骤如下。
(1)利用绘图软件提取辙叉不同截面数据后各自形成独立的数据文件,按照各截面至辙叉趾端的距离,将辙叉不同截面数据、基本轨一侧标准钢轨截面数据和车轮踏面数据依次输入软件的用户操作截面。
(2)根据给定的辙叉设计图中各股轨线平面位置关系,如各关键部位钢轨截面相对于轨道中心线的距离,特别是轮载过渡段翼轨心轨截面相对于轨道中心线的位置关系,以及轮轨内侧距等,在程序中实现将(1)中提供的数据文件转化为反映实际轨线布置情况下的轮轨坐标文件。
(3)利用给定的步长和循环完成轮对不同横移量情况下沿辙叉全长的轮轨接触参数(包括竖横向不平顺、轮对侧滚角、踏面等效锥度)的计算和输出以及轮轨接触点坐标值的输出。用户可以根据实际需要,任意设定计算步长大小,包括沿辙叉方向断面插值间距,任意截面寻找轮轨间最小距离时的插值间距,通过设定步长达到用户所需的计算精度。
(4)最后生成的计算结果数据以文件的形式保存在用户设定的路径中,方便用户调用分析。
3轮轨接触关系算法验证
3.1试验验证
为验证轮轨接触关系算法和软件的正确性,对辙叉走行方向轮轨接触点变化情况以及辙叉各关键断面轮轨接触点变化规律进行测量(图7),测量结果与软件计算结果进行对比分析。现场试验采用的轮对完全按照LM型踏面标准尺寸进行加工,辙叉为尚未上道使用的60 kg/m钢轨12号合金钢组合辙叉(翼轨无加高且为标准钢轨截面)。试验通过道尺获取轨距测量点,同时在车轮踏面标注轮缘厚度测量点,并根据几何关系确定的轮对无横移时轨距测量点对应的车轮踏面点。接触点的确定采用在车轮踏面及钢轨轨头涂抹标识性涂层,通过读取轮轨接触后涂层所留痕迹即可量取接触点位置。需要说明的是,通过上述设置只能实现轮对与钢轨不同横移量下轮轨接触点的低精度测量,来初步判断轮轨接触点的变化规律,而在高精度测量中则需要采用钢轨廓形测试仪进行辅助测量。

图7 轮轨接触点现场测试
(1)沿辙叉走行方向轮轨接触点变化
从辙叉趾端开始每隔50 mm的断面进行测量,获得轮对无横移时沿辙叉走行方向轮轨接触点的位置,计算出辙叉的竖、横向不平顺,并与软件计算结果进行比较,如图8、图9所示。
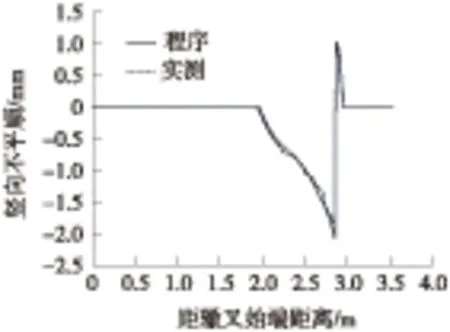
图8 竖向不平顺
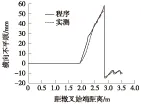
图9 横向不平顺
图8、图9反映了磨耗型踏面车轮在轮对无横移时通过合金钢组合式固定辙叉时竖横向不平顺的变化规律。对比结果表明,利用软件与实测数据分别计算的辙叉竖、横向不平顺变化规律基本相同。在辙叉咽喉前,实测和软件计算结果完全吻合,即不存在不平顺;从辙叉咽喉至心轨71 mm断面范围内,辙叉存在明显的结构不平顺,实测和软件计算结果变化规律一致,且软件计算所得竖向不平顺最大值略大于实测结果,存在一定的安全余量,表明采用该计算软件可以完成对辙叉区结构不平顺的计算和评价。
(2)辙叉关键断面轮轨接触点变化
通过现场实测,得到了辙叉区各关键断面轮轨接触点的变化范围及变化规律。辙叉咽喉、心轨顶宽20 mm和50 mm断面的实测接触点位置与相应的软件计算结果对比如图10所示。需要说明的是,程序计算的接触点范围是在理想状态下轮对横移量为-12~12 mm范围内取得的,而实际情况下由于护轨和轮缘槽的横向限位,轮对横移范围均未达到12 mm,因此图中实测接触点较少。由图上实测和计算接触点位置变化规律可以看出,实测与计算的各关键断面轮轨接触点变化规律基本一致,相同横移量情况下接触点位置差别较小,同时与区间线路轮轨接触点的变化规律[16]相同。
综上所述,本文对辙叉区轮轨接触点的各项计算结果与实测结果均较为接近,且变化规律相同,这说明编制的辙叉区轮轨接触关系算法正确,计算软件能够较好地反映辙叉区的轮轨接触特性。
3.2翼轨加高优化设计
固定辙叉存在有害空间,当轮对逆向进入辙叉区时,轮对从咽喉驶向心轨直至完全作用于心轨的过程中,辙叉侧车轮接触点半径减小,轮对侧滚角有所增大,轮对重心先下降再逐渐上升到原来的高度,造成了辙叉区结构不平顺的产生。目前我国固定辙叉采用翼轨加高技术来减缓结构不平顺,采用本文提出的固定辙叉区轮轨接触算法对该项优化设计的轮轨接触特性进行验证和校核。以心轨尖端至顶宽50 mm范围内翼轨加高1、2 mm和无加高分别设置3种工况,分析磨耗型踏面车轮通过60 kg/m钢轨12号道岔整铸辙叉时结构不平顺、等效锥度、轮对倾角的变化规律,计算结果对比如图11所示。
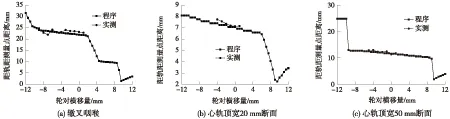
图10 各关键断面轮轨接触点分布
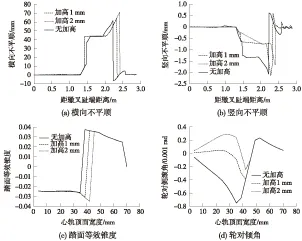
图11 轮轨接触参数
从图11可知,随着翼轨加高量增大,轮对倾角、踏面等效锥度均随之减小,轮轨过渡范围内的竖向不平顺也明显降低,说明翼轨加高起到缓冲竖向结构不平顺的作用,但是翼轨加高造成横向不平顺的增大表明了固定辙叉采用翼轨加高技术在降低竖向动力作用的同时会增大横向动力作用,因此应综合考虑横向不平顺的增加对轮轨相互作用的不利影响,翼轨加高值不宜过大。
4结论
本文以区间轮轨接触关系为基础,考虑固定辙叉轨头外形不规则变化和轨迹线的不连续性,提出了固定辙叉区轮轨接触关系算法,并通过程序加以实现,利用现场试验和模型计算对其正确性和可行性进行了验证。
(1)针对轮对无横移通过固定辙叉时,左右车轮滚动半径变化导致其接触点位置不对称的情况,推导了固定辙叉主要轮轨接触参数的计算方法,并通过软件编制实现了算法的程序化,提高了计算精度和效率。
(2)从软件计算与现场实测两个方面对辙叉纵向和各关键断面的轮轨接触点变化情况进行对比分析,辙叉区轮轨接触点计算结果与实测值变化规律相同且较为接近,符合实际轮对过岔时轮轨接触点的变化特性,验证了固定辙叉轮轨接触关系算法及软件的正确性和可行性。
(3)以固定辙叉区翼轨加高为例,采用该软件分析其轮轨接触关系并加以评估,可知翼轨加高一定程度上可以减小辙叉竖向不平顺。同时反映本文所提算法和计算软件能够用于固定辙叉结构优化设计,也为轮轨动力学的进一步研究提供了技术支持。
参考文献:
[1]王开文.车轮接触点迹线及轮轨接触几何参数的计算[J].西南交通大学学报,1984,19(1):89-99.
[2]Piotrowski J, Ch Ollet H. Wheel-rail Contact Models for Vehicle System Dynamics Including Multi-point Contact[J]. Vehicle System Dynamics, 2005,43(6-7):455-483.
[3]任尊松.轮轨多点接触计算方法研究[J].铁道学报,2011,33(1):25-30.
[4]Sergey Z. Problems With Wheel and Rail Profiles Selection and Optimization[J]. Wear, 2008,265:1266-1272.
[5]Simon I et al.车辆-轨道相互作用研究方法的新进展[J].国外铁道车辆,2010,47(5):1-5.
[6]任尊松.车辆动力学基础[M].北京:中国铁道出版社,2009:23-24.
[7]Hiroyuki S, Yoshimitsu T, Ryosuke M. Analysis of Wheel/Rail Contact Geometry on Railroad Turnout Using Longitudinal Interpolation of Rail Profiles[J]. Journal of Computational and Nonlinear Dynamics, 2011,6(4):1-5.
[8]任尊松,翟婉明,王其昌.轮轨接触几何关系在道岔系统动力学中的应用[J].铁道学报,2001,23(5):11-15.
[9]全顺喜.几何不平顺对道岔区轮轨接触几何关系的影响[J].铁道标准设计,2013(3):17-22.
[10]任尊松,刘志明,金学松.心轨轨顶降低值对轮岔动态相互作用影响研究[J].铁道学报,2009,31(2):79-83.
[11]徐井芒,王平.基于轮轨廓型的固定辙叉优化设计方法[J].中国铁道科学,2014,35(2):1-6.
[12]王树国,葛晶,司道林,等.固定辙叉查照间隔及心轨加宽研究[J].中国铁道科学,2014,35(1):7-12.
An Algorithm of Wheel/Rail Contact Geometry for Rigid Frog and Software Development
ZHAO Wei-hua1,2, WANG Ping2, HUANG Wei1,2
(1.College of Civil Engineering, Fujian University of Technology; 2. Fujian Provincial Key Laboratory of Advanced Technology and Informatization in Civil Engineering, Fuzhou 350118, China; 3.MOE Key Laboratory of High-speed Railway Engineering, Southwest Jiaotong University, Chengdu 610031, China)
Abstract:Based on wheel/rail contact theory, an algorithm is proposed to obtain accurate wheel/rail contact parameters of rigid frogs and the corresponding software is developed in consideration of the change of complex railhead profiles and the discontinuity of gauge lines in rigid frogs. The LM wheel tread passing over No.12 alloy steel combination frog is simulated by field test, and wheel/rail contact points along the longitudinal direction and key cross sections of frogs are measured and compared with those calculated by software. This software is used to analyze the influences on wheel/rail contact parameters when wing rails of cast manganese steel frog are heightened. The results show the variation regularities of wheel/rail contact points measured by field test agree with those of points calculated by software; the reasonable heightening of the wing rail can optimize the wheel/rail contact relationship and reduce vertical irregularities in rigid frogs, which validates the correctness of the algorithm and the feasibility of the software; the software is an accurate and efficient tool to optimize the design of wheel/rail contact relationship in the rigid frog zone.
Key words:Turnout; Rigid frog; Wheel/rail contact geometry; Software development; Irregularity; Optimization design
文章编号:1004-2954(2016)05-0015-05
收稿日期:2015-09-17; 修回日期:2015-10-08
基金项目:国家自然科学基金资助项目(51508098,51308081),福建省教育厅资助项目(JA15327)
作者简介:赵卫华(1984—),女,讲师,博士,E-mail:whzhao.good@163.com。
中图分类号:U213.6
文献标识码:A
DOI:10.13238/j.issn.1004-2954.2016.05.004
