软质管线收卷机构PID控制研究

皮嘉立，张世富，谢昌华

(后勤工程学院　a.军事供油工程系; b.国家应急救灾装备工程技术中心，重庆　401311)



软质管线收卷机构PID控制研究

皮嘉立a，张世富b，谢昌华b

(后勤工程学院a.军事供油工程系; b.国家应急救灾装备工程技术中心，重庆401311)

摘要：为使软质管线收卷机构在受到负载力矩扰动的情况下收卷机构的控制系统拥有良好的瞬态与稳态性能，采用PID控制器对控制系统进行调整。用传递函数的方法建立控制系统的模型并采用根轨迹法对PID控制器参数进行分析优化。同时用Simulink建模的方法建立控制系统的模型并采用正交试验法则对PID控制器参数进行优化；计算结果表明：传递函数建模根轨迹法分析的优化结果与Simulink建模正交试验法分析的优化结果比较吻合，传递函数模型与Simulink模型得到相互印证。根轨迹分析法的结果为正交试验法的分析提供了初始的水平数取值范围。正交试验法的分析结果为进一步试验分析指明了方向。两种优化方法的综合运用使PID控制器参数的优化效果得到提高。

关键词：根轨迹分析；PID控制器参数；Simulink仿真；正交试验法

软质管线收卷机构是一种靠摩擦轮传动牵引力的软管收卷装置，装载于软质管线作业车的收卷机头展收机构之上。软质管线控制系统的功能是实现软质管线的收卷速度VH与软质管线作业车的车速Vd同步。经分析，建立了软质管线收卷机构在外力矩不产生波动的情况下的控制模型与矫正装置的模型。在实际中许多情况都会产生外力矩的波动，如路面不平顺、软管的扭曲变形等因素都有可能造成负载扭矩的波动。故须对软质管线收卷机构在外力矩波动的情况下建模分析。

1PID控制器根轨迹优化分析

1.1控制系统传递函数模型建立

考虑负载力矩的情况，控制系统的模型可以表达成以下控制框图(图1)，

图1　控制系统的控制框图

其中

将开环控制系统的负载力矩的力矩变化信号转化为阶跃信号，上式经过Laplace变换，得新的开环传递函数：

从图2中可以看出，系统的根轨迹在实数域有两条发散的轨迹曲线，这个控制系统不是稳定的。PID控制器由积分控制器、微分控制器、比例控制器并联而成，通过优化3个控制器的增益值，可以使控制系统的稳定性和瞬态、稳态性能得到改善[1]。加入调整环节后的PID控制系统如图3所示。

图2　控制系统的根轨迹

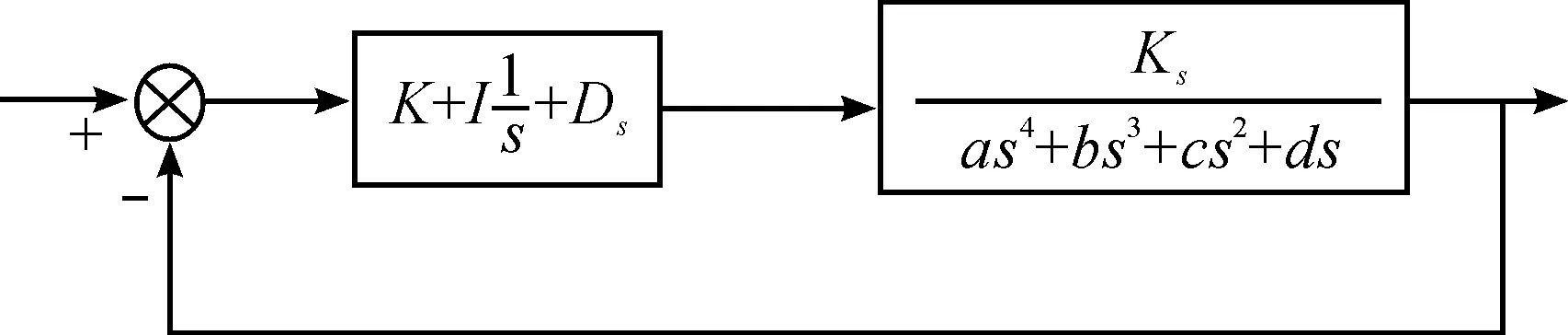
图3　加入PID控制器的传递函数控制方框

控制器为PID控制器，其传递函数为

其中，K为比例增益，I为积分增益，D为微分增益

1.2根轨迹分析

在传递函数模型中PID控制器实际上是通过设置调整零点位置[1]，使得根轨迹向左方移动，从而增加系统的稳定性，减小系统响应的调整时间，最终使系统达到最佳状态。收卷机构控制系统的开环传递函数包含4个极点，分别是两个复极点s=-5.51+1 243.53i和s=-5.51+1 243.53i和2个重极点s=0；同时还包含两个零点-α、-β。若令α=β，此时，PID控制器有两个参数(K，α),可以使优化过程更简单。当α为一个较小值即α=1时，可以做出闭环系统的根轨迹总体和闭环系统的根轨迹附近图如图4所示。

从图4中可以看出根轨迹主要由2条轨迹线组成。其中根轨迹线为曲线形的系统为欠阻尼系统ζ<1，根轨迹线为直线形的系统为临界阻尼系统ζ=1。当ζ<1，系统欠阻尼的时候，系统的闭环极点位于如图所示的曲线上，可以把闭环极点用极坐标的形式表达，其中ζ对应于一条与实数轴成Φ夹角的直线，极点与原点的距离由无阻尼自然频率ωh确定。因此，闭环极点位于s=ωhcosΦ±ωhsinΦi，根据幅角条件，在此点上有如下关系，∠G(s)H(s)=±180°(2k+1)，由闭环极点的幅角关系可以确定开环零点的大致位置，即α、β的搜索范围。计算结果显示闭环极点在曲线形根轨迹线上的系统的增益K<0.001，ζ<1，曲线形根轨迹线对应的控制系统为欠阻尼系统，系统产生的瞬态响应曲线拥有很大的超调量，故不应使闭环极点位于曲线轨迹上。介于此我们希望闭环极点位于实数轴成的直线上，即系统的阻尼ζ=1，增益K>0.001。这样PID控制系统的设计问题就转化为寻找一组增益K值和-α、-β的零点值，使闭环系统的单位阶跃响应满足设计要求的问题。由上面的根轨迹分析可知增益K与两个零点-α、-β的合适搜寻范围，即K>0.001，0<α<2，0<β<2。由此可以编写Matlab程序来逐点搜寻K与α、β的组合，使系统的瞬态响应满足调整时间、最大超调量、跟随误差等的相关瞬态、稳态指标的要求[5]。部分计算结果如表1所示。

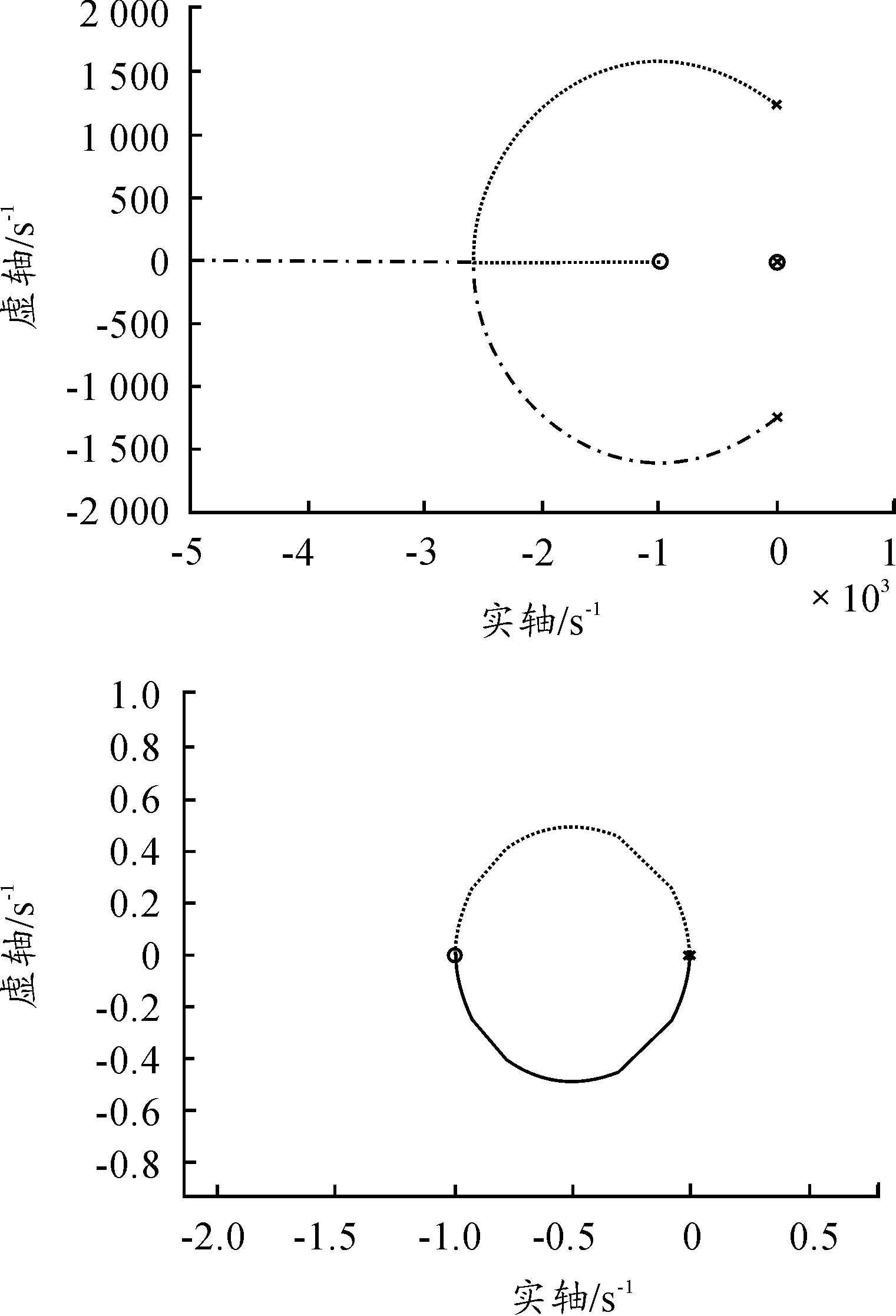
图4　加入PID控制器系统的根轨迹

经计算发现当Γ=2，α=0.61，β=0.76时，控制系统的综合性能较好，瞬态响应的调整时间小于1S，稳态精度达到99.99%。故选取Γ=2，α=0.61，β=0.76的PID控制器。由于两个零点值与PID控制器的积分增益i和微分增益d有如下的换算公式，

将Γ=2，α=0.61，β=0.31代入上式，得到PID控制器的比例增益k=1.84，积分增益i=0.37，微分增益d=2，故优化的PID控制器的参数为k=1.84，i=0.37，d=2。

2正交试验法PID控制器参数优化

2.1控制系统Simulink模型建立

传递函数设计控制系统的方法直观，易于程序实现，但是缺陷也比较明显。传递函数仅有一个输入一个输出，意味着传递函数只能模拟车速与负载力矩同时发生变化的情形，而实际情况中往往是车速并没有发生改变而负载力矩却由于软管中软管充水不均匀，软管的铺设不平直等原因造成负载力矩上下波动。根据前面的分析可以把软质管线收卷机构的控制方程分成3个部分，阀的流量特性方程，马达的流量特性方程，马达和收卷机构的负载特性方程。根据控制原理方程，运用Simulink的方法可以建立的控制模型。子模块Subsystem主要表示阀的流量特性方程，子模块Subsystem1主要表示马达的流量特性，子模块Subsystem2主要表示马达及收卷机构的负载特性。利用子模块的输入和输出相互耦合关系可以搭建如图 5所示的控制系统仿真的总体框图，

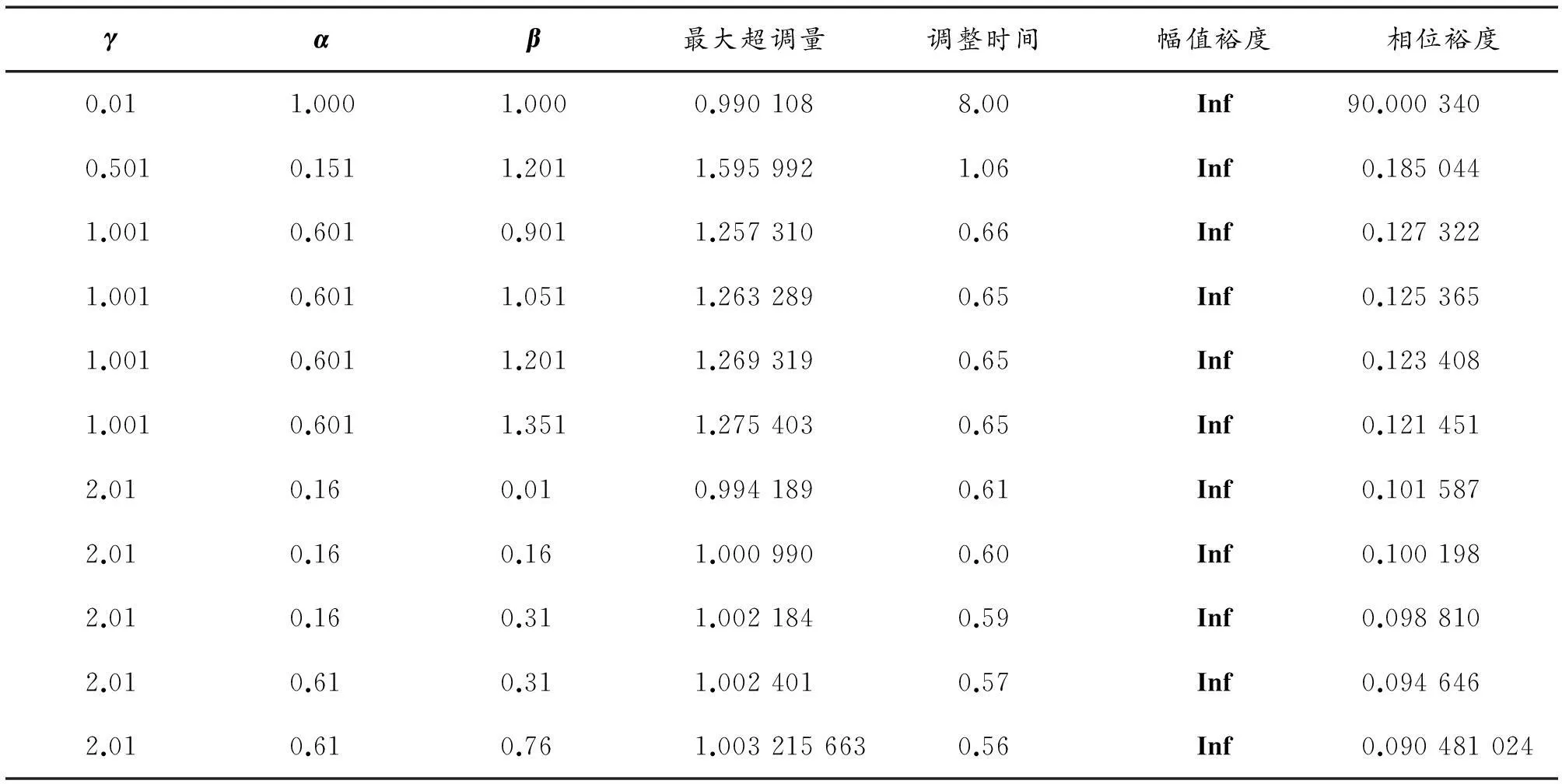
表1　优化计算结果

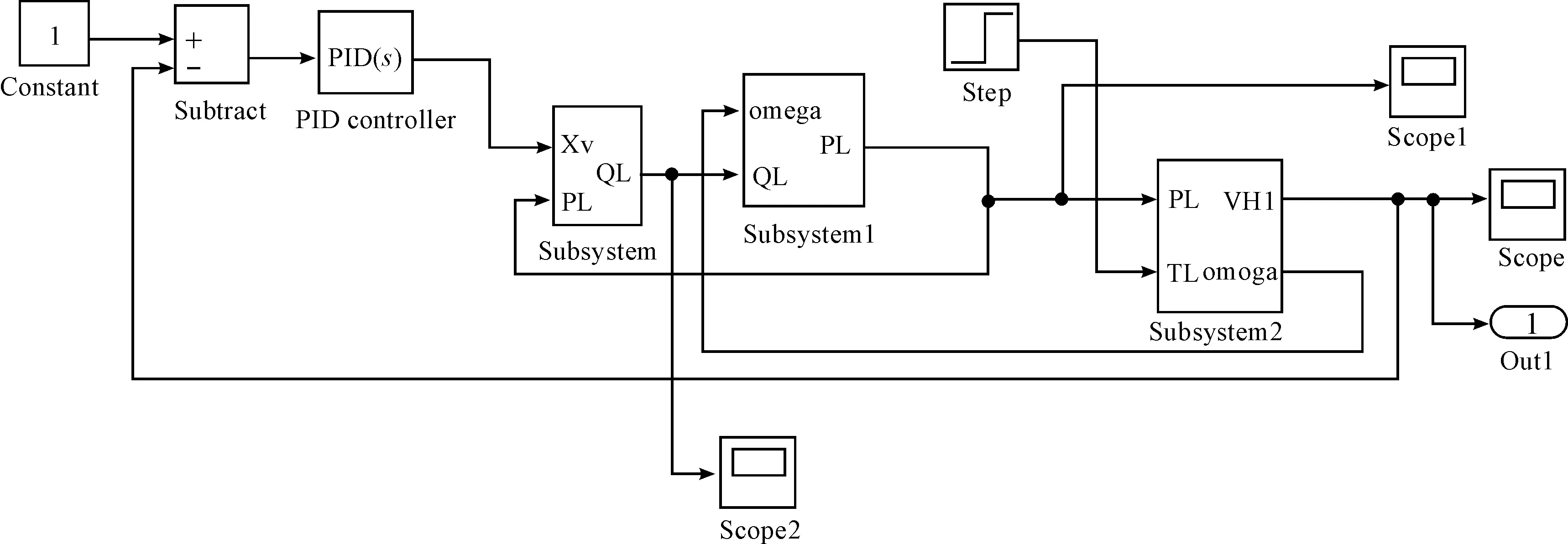
图5　控制系统Simulink仿真的总体框图

2.2正交试验法分析

PID控制器参数的优化方法有很多，如齐格勒-尼科尔斯法、频率响应法、计算最佳化法等[11-13]。这些方法各有优缺点，齐格勒-尼科尔斯法要求系统的输出呈现持续振荡，如果无论怎么选取k的值都不能使系统产生振荡，则不能采用此法。频率响应法能使系统的稳定性提高，但是指标过于单一。计算最佳化法能搜寻出满足要求的PID控制器的参数，但是程序设计需要3层嵌套，PID控制器参数的选取比较盲目，控制系统的性能指标多与2个就难于判断孰优孰劣。要用试验的方法确定PID控制器的参数，应确定系统的综合控制性能指标以判断控制系统瞬态性能和稳态性能否达到平衡。首先采用系统的稳定性权函数表征系统的稳定性，可表达为下式：

以上4个指标分别反映了控制系统的稳态精确性、响应相对稳定性、达到稳定状态调整速度和功率元件的大小。综合上述的4个性能指标和4个权函数可以推导出系统的综合性能指标如下：

其中A、B、C 3个权函数分别取A=100，B=5，C=1。借助正交试验的方法调节PID控制器，通过正交试验设计可以大大减少试验次数，分清各个因素的主次顺序，判断因素对试验指标影响的显著程度，找到试验因素的优水平和试验范围内的最优组合[9-11]。控制系统的正交试验包含k、i、d 3个因素，根据根轨迹的分析，比例增益在1～3取值，积分增益在0～3取值，微分增益在0～3取值，比例增益、积分增益、微分增益3个试验因素之间不考虑交互作用，得水平因素表如表2所示。

表2　PID控制器参数水平因素

以减少试验次数，选择小号的正交表为原则，另外，为考察试验误差，最好有一列空列，故选用L9(34)正交表，进行试验。以综合性能指标来评价系统的控制性能。若综合性能指标越大则控制性能越好，得到试验结果如表3所示。

表3　正交试验结果

为进一步分析比例增益、积分增益、微分增益3个试验因素与试验指标的关系，找出指标随因素变化的规律和趋势，下面对试验的结果进行极差分析和方差分析。极差分析结果如表4所示。

表4　极差分析

表4中Ti表示某一列上水平数为i时所对应的试验指标；R为极差，是任一列因素各水平的试验指标最大值、最小值之差，即R=max(T1,T2,T3)-min(T1,T2,T3)，R反映了各列因素的水平变动，试验指标的变动幅度。根据极差R的大小，微分增益的极差最大，比例增益其次，积分增益再次，就可以判断影响综合指标因素的主次顺序为K、I、D。

极差分析具有简单直观、计算量小等优点，但直观分析法不能估计误差的大小，不能精确地估计各因素的试验结果影响的重要程度，为了弥补极差分析法的不足，对正交试验结果进行方差分析(表5)。

表5　方差分析

给定显著水平α=0.1，由表5求得fα值，即α分位点等于3.46。从图表中看出d的f值fd>fα，则认为微分增益d对试验结果的影响是显著的。

为了更直观地反映因素对试验指标的影响规律和趋势，以因素水平为横坐标，试验指标值(Ti)为纵坐标，绘制因素与指标趋势图，如图6所示。

根据图6可以初步确定d的最优取值水平为3，而k、i、d的最优取值可以通过重新编制正交试验表格，多次试验取得。由图可知k、i的水平数为2时，指标较其余水平数指标高，故最优取值在k、i的水平数为2的左右，故可以用二分法或者用黄金分割法不断缩小水平数的取值范围，使得k、i的取值收敛于一个值。经试验测定，最终k、i的取值收敛于k=2，i=1，d=2。这与根轨迹法的PID控制器的参数优化结果比较吻合。

图6　因素与指标趋势

3结论

增大比例增益在减少响应时间，降低稳态误差的同时，会降低控制系统的稳定性；积分控制消除稳态误差的同时，会导致振幅缓慢衰减和振幅不断增加的振荡响应；微分控制使系统控制器的灵敏度提高，同时会增加系统的阻尼。优化比例、积分、微分控制环节的增益可以使3个控制环节相互矛盾的特性得到协调。PID控制器根轨迹优化分析的方法建立在传递函数模型上，直观简单，计算量较大，用Simulink结合正交试验法的优化方法全面精确依赖对控制系统初步分析得出控制器参数的优化范围，2种优化方法的综合使用让PID控制器参数的优化效果得到提高。

参考文献：

[1]KATSUHIKO O.现代控制工程[M].北京:电子工业出版社,2011(8):373-385.

[2]孙大卫,张国良,陈励华.基于根轨迹的直流伺服电动机PID控制器参数确定法[J].实验技术与管理,2009(4):38-41.

[3]邵中年,张志瑞.基于根轨迹法的随动系统PID控制[J].四川兵工学报,2012(2):94-96.

[4]金园园,王正仕,陈辉明,等.基于根轨迹的单相逆变器PID控制器设计[J].机电工程,2008(2):83-85.

[5]栗建中.坦克火炮控制系统设计与仿真[D].南京：东南大学,2006:22-30.

[6]吴剑威,唐立新.基于根轨迹法与串联PID法的激光操作控制系统设计[J].合肥师范学院学报,2010(3):39-40.

[7]邓家祺.水轮机调速系统的根轨迹校正与PI、PID调速器的参数选择[J].大电机技术,1982(2):53-63.

[8]张显明,童调生.利用多变量根轨迹设计最优PID调节器[J].控制与决策,1990(1):47-50.

[9]王幼民,范恒灵.基于正交试验法的电液伺服系统PID控制[J].农业机械学报,2007(7):196-198.

[10]金波,朱世强,张光琼,林建亚.用正交试验法整定PID控制器参数[J].中国机械工程,2000(6):91-92.

[11]王雷,唐敦兵.基于正交试验的PID控制可重构制造系统生产能力优化研究[J].中国机械工程,2009(12):1430-1433.

[12]黎红,郭春秋,崔立辉,张沙.正交试验法在直流电动机调速控制系统PID参数整定中的应用[J].机械制造与自动化,2012(1):150-152.

[13]彭安华,孙旭东,王智明.基于正交试验法的PID控制器参数整定[J].机械科学与技术,2011(6):1028-1032.

(责任编辑杨继森)

本文引用格式：皮嘉立，张世富,谢昌华.软质管线收卷机构PID控制研究[J].兵器装备工程学报，2016(5):98-103.

Citation format:PI Jia-li,ZHANG Shi-fu,XIE Chang-hua.Research on PID Control of Rolling Hose Mechanism[J].Journal of Ordnance Equipment Engineering,2016(5):98-103.

Research on PID Control of Rolling Hose Mechanism

PI Jia-lia,ZHANG Shi-fub,XIE Chang-huab

(a.Department of Petroleum Supply Engineering; b.National Engineering Research Center for Disaster & Emergency Relief Equipment,Logistic Engineering University,Chongqing 401311,China )

Abstract:In order to make the control system of the rolling hose mechanism have good transient and steady state performance under the condition of load torque disturbance,the PID controller was used to adjust the control system.The model of the control system was established by transfer function method and the PID controller’s parameters were optimized by the root locus method.At the same time,the model of the control system was established by Simulink modeling,and the PID controller parameters were optimized by the orthogonal test.The results show that the optimization results of the root locus method of transfer function modeling are consistent with the optimization results of the Simulink modeling orthogonal test.The transfer function model and the Simulink model can be confirmed by each other.The results of root locus analysis provide the initial value range of the level for the analysis of the orthogonal test.The analytical results of the orthogonal test method indicated the direction for further experimental analysis.The comprehensive utilization of the two optimization methods can improve the optimization for parameter of PID controller.

Key words:root locus analysis; parameters of PID controller; Simulink simulation; orthogonal tests

doi:【信息科学与控制工程】10.11809/scbgxb2016.05.024

收稿日期：2016-01-13；修回日期：2016-02-25

基金项目：国家科技支撑计划(2014BAK05B00)；油料装备寒区试验基地数据采集系统研究(YX214L040)；SF防渗漏双层罐应用技术研究及超低压液位控制装置研究(BX213C005)

作者简介：皮嘉立(1991—)，男，硕士，主要从事油料装备研究。

中图分类号：TH39

文献标识码：A

文章编号：2096-2304(2016)05-0098-06