试分析图形图像压缩的常见方法技巧

王芳

摘要：压缩是图形图像在传输、储存等方面所必须经历的一个环节，因为图形图像若是不经过压缩处理，其所需占用的内存空间是比较大，这不仅会造成传输效率较低，也会给储存造成麻烦。在此基础上，就出现了一些压缩图形图像的方法，这些方法在使用的过程需要注意一些关键要点。由此，本文首先针对压缩图形图像的基本原理进行了分析，然后对压缩图形图像的方法进行了简单的阐述，最后着重从经典压缩方法、小波变换压缩、复合压缩等几种方法着手展开分析其中技巧，希望可以对相关人员提供一定的参考。

关键词：图形图像；压缩；原理；方法；技巧

中图分类号：TP18 文献标识码：A 文章编号：1009-3044（2016）12-0199-02

图形图像是一种信息载体，其能够承载较大量的信息，而且主要是通过数字化的方式进行表达、传输和储存。在数字化之后，图形图像具有带宽宽、信息量大等特点，而且可以实现不同的信息功能。因此，需要对图形图像进行压缩，在保持其信息内容的基础上，尽量减少占用，提高图形图像的使用效率。

1 压缩图形图像的基本原理

从图形图像所承载的数据来看，其存在一定的冗余，这就给压缩提供了可能。从信息论创始人Shannon所表达的观点可以发现，可以将冗余度和信息的组合看做是数据信息，削除其中的冗余度，不仅可以保证信息的完整性，还可以使数据更为精简。这里所指的冗余度，是因为图形图像各个像素之间存在一定的相关性，通过编码手段将其删除，就可以减少冗余度，实现数据压缩。

图形图像的冗余一般包括了六个方面：一是时间冗余，即两个连续帧之间存在的冗余；二是空间冗余，即是像素点之间的相关性；三是结构冗余，即图形图像中存在的纹理结构；四是知识冗余，这主要是指一些固定结构，比如人体头像；五是视觉冗余，这是指肉眼难见的图像失真；六是信息熵冗余，即指单位熵小于其信息量。

基于图形图像所存在的六个方面的冗余，压缩处理也可以从这六个方面对应展开。在具体的压缩原理上，主要基于两个基本的原理，即人的视觉心理特征和图形图像的相关性。在视觉心理特征这个方面，因为人体视觉系统对图形图像的感知存在一定的界限范围，超出界限范围之外的图形信息人体视觉是感受不到的。所以，在进行图形图像的压缩处理时，就可以将超出人体视觉界限范围之外的部分进行压缩。而图形图像的相关性，主要就是上文所致的冗余度，在压缩时尽量消除图形图像中的冗余度即可。

2 压缩图形图像的方法概述

对图形图像进行压缩，其典型的系统主要是由变换部分、量化部分和编码部分组成的。变换部分就是对原始输入图形图像和变换之后的图形图像的对应关系进行了展现，其也可以被称为去除相关，对图形图像中的冗余度进行压缩处理。量化部分就是把经过变换处理之后得到的图形图像进行输入处理，由此得到有限数目的一些符号。这一部分会造成信息损失，是有损压缩和无损压缩的关键区别，无损压缩不存在这一环节。编码部分就是对图形图像中经过变换的系数进行二进制编码，可以使用变动长度编码，也可以使用固定长度编码。

在具体的压缩方法上，从不同的压缩目的出发，可以有不同的方法分类。比如，从信息保持程度这个角度切入，在压缩方法上就可以分为三个类别，第一是牺牲部分数据的信息损失型压缩方法，这主要是为了获取较高的压缩比，像图像传输、多媒体以及数字电视等，对该类压缩方式运用较多。但是这种压缩会产生人体视觉不可分辨的信息损失，也被称为有损压缩。第二是信息保持型压缩，这不会产生信息损失，最主要的特点就是信息不会失真。但是该种方法的压缩比有限，主要在图像存档上使用较多。第三是抽取特征值压缩，将其与非特征值全部去除。这种压缩方式仅仅是保留有用的信息，对无用的信息悉数提出，属于信息损失型压缩。

若是从基本的方法原理上对压缩方法进行分类，则可以分为四种。一种是预测压缩，即只是针对图形图像的冗余度和相关性进行压缩，只编码新信息。二种是像素压缩，这主要是对图形图像的每个像素进行单独处理，像行程编码、熵编码、脉冲编码调制等，都属于这类压缩。三种是变换编码，这主要是对图形图像进行某种变换，通过较少的数对大量信息进行表示，像离散余弦变换、小波变换以及离散傅里叶变换都属于此类。四种就是其他方法了，如矢量化、混合编码以及LZW算法等。

3 几中常见图形图像压缩方法技巧分析

3.1 经典方法

在图形图像的压缩处理上，出现过许多较为经典的方法，这些方法在当时都得到了广泛的运用与传播，发挥出了巨大的作用。下面就针对LZW编码、行程长度编码等几种经典压缩手段进行阐述。

对于LZW编码而言，其基本原理就是将每个字节所对应的值，和下一个字节对应的值匹配起来，组成一个字符对，并且对其设定一个代码。如此，在该字符对再次出现的时候，就可以通过这一设定的代码对其进行表示。LZW编码中的代码不仅仅可以对一串同值数据实现取代，还可以对不同值的数据进行取代。在图形图像中，若是一些不同值的数据大概率出现重复，那么也可以通过一定的代码对其进行取代，实现压缩的目的。

对于行程长度编码，其是一种最为简便的图形图像压缩方法，具体做法就是通过一个独立值和计数值，对一系列的重复值进行取代。比如，在图形图像的信息数据中，若是存在这样一个字母序列，如aaabbbcccccdddd，就可以用3a3b5c4d这样一个编码对其进行取代，如此就实现了压缩处理。这种方法针对长重复值的压缩处理非常有效，尤其是存在颜色相同、大面积连续阴影的图形图像，使用该种方法进行压缩效果优良。像PCX、GEM以及TIFF等文件，都使用这种压缩方法。

矢量量化编码就是基于图形图像数据间存在的高度相关性，将其输入到数据序列分组之中，对每一组中的m个数据，可以组成一个m维的矢量，进而实现一次性编码，这样就一次性实现了对多个点的量化处理。而基于Shannon失真理论，矢量量化编码对于无记忆信源，效果要优于标量量化编码。

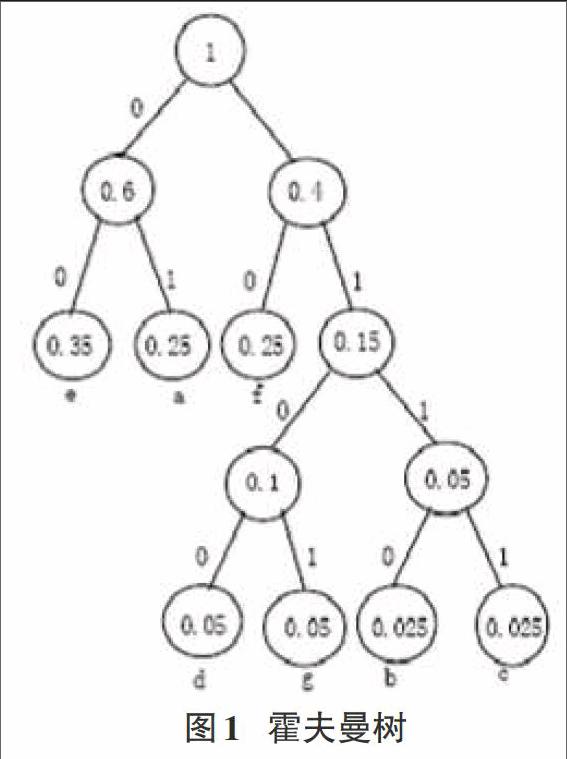
霍夫曼编码是经典压缩技术中的一种可靠技术，其是基于统计理论的一种压缩编码方法。霍夫曼编码的核心原理就是通过长度不固定的编码对原始数据进行替代，从而实现图形图像的压缩。该种方法最早是针对文本文件进行压缩而出现的，在实践运用中逐步发展创新，逐步在图形图像的压缩中进行使用。在实际运用中，霍夫曼编码体现出了一定的特点，即高频率的值，其对应的编码越短；低频率的值，其对应的编码越长。比如，针对一个信源（a，b，c，d，e，f，g），分别假设这些值出现的概率为（0.25，0.025，0.025，0.05，0.35，0.25，0.05）。将这些值按照出现频率大小进行排列，以最小值构成一颗二叉树，将较大的值置于左边，两叶子节点的频率和作为根节点。同时，将原本排列中的两个最小节点删除，将新得到的根节点插入其中，并且保证大小顺序不变。这样重复执行，直达最后达到为1的根节点，这时就可以达到一个霍夫曼树，如下图所示。

3.2 小波变换压缩

小波变换压缩是一种现代化的图形图像压缩方法，其核心原理就是将图形图像分解成为细节图像和逼近图像之和，使其代表不同的结构，通过快速算法实现压缩处理，这样可以得到非常可观的压缩比。在小波变换压缩的实际使用中，首先需要通过某一小波函数对图形图像进行小波变换，然后在此基础上通过四个通道所表现出的不同情况，对其进行分别量化编码。比如，对于高频频段，可以使用量化很少的级别；对于中间频段，可以使用量化较少的级别；对于低频频段，可以使用量化较多的级别。如此，可以再分别对待复原信号的重要程度的基础上有效提高压缩比，并且确保不会产生较大的失真。在静态图像的压缩中，小波变换压缩方法已经得到了业界的公认，在JPEG2000标准中，也对这一方法进行了规定。在图形图像的压缩处理上，小波变换的实质就是对原始的图形图像进行了小波系数重组，利用处理后得到的小波系数实现图像的恢复。根据JPEG2000标准中的相关规定，利用小波变换进行图形图像的压缩处理，最为常用的就是支集长度为7和9的双正交小波。通过实践表明，小波变换压缩处理在容错性上表现优良，非常适合日常的实际运用。

3.3 分形编码压缩

根据物质本身存在的自相似性特点，因此可以再进行图形图像编码的过程中，将相关信号分解成为多个分形子图，对迭代函数系统的代码进行提取。在进行图形图像的恢复时，依照之前所提取的代码的迭代规律，通过迭代重构实现子图还原。通过分形编码压缩图形图像时，可以通过六个步骤进行。第一，对原始图像进行分割处理，在保证每个子图具备一定分形结构的基础上将原图划分为多个子图。要完成这一步骤，需要通过图像处理、计算机视觉等相关技术，并且多次反复操作才能有效完成。第二，对每个子图进行函数代码的提取，这需要将子图放置在计算机上，通过伸缩、平移、旋转等手段进行处理，依靠压缩子图获取仿射变换参量一组，由此得到函数代码。第三，通过经典编码方法对该函数代码进行编码。第四，再进行译码处理想，形成新的代码。第五，利用新形成的代码，进行子图重构。第六，完成子图重构之后，通过拼图处理恢复原图。通过分形编码压缩的具体流程不难看出，该方法就是将原图进行分割，然后对各个子图进行代码编译，再通过编译后的代码恢复子图，再将子图拼回原图。这一过程使得图形整体和局部之间存在一定的仿射性或是相似性，具有较好的压缩比。

3.4 离散余弦变换

离散余弦变换压缩手段从性质上说来和傅里叶变换是一种相关的压缩技术手段，两者比较类似，但是离散余弦变换只能使用实数。但是，离散余弦变换在实际的使用过程中表现出了强力的能量集中特点，大部分自然信号的能量都可以集中到图形图形经过离散余弦变换之后的低频部分。在信号和马尔科夫统计特性相接近的时候，其相关性与K-L变换性能是比较接近的。在对图形图像进行压缩处理时，离散余弦变换会发生一定的损失，也就是有损压缩。不论是对静止图像还是动态图像，离散余弦变换压缩所产生的损失是不可避免的。

3.5 复合压缩

不同的压缩方法适用的场合条件存在一定的区别，压缩效果也不一样。可以说，不同的压缩方法有其各自的优点，也有其各自的缺点。因此，综合不同技术的优点，摈弃不同技术的缺点，是图形图像压缩方法所需要关注的问题。由此，也就提出了复合压缩的相关思想。复合压缩就是将两种或以上的压缩技术进行综合，实现技术的融合渗透，形成一种全新的压缩方式。比如，在小波变换的基础上，可以将分形图像压缩引入其中。可以将小波变换和矢量量化结合起来，对图形图像进行压缩处理。也可以将基于基础表的压缩技术和基于非均匀分割的压缩技术综合起来。总的说来，复合压缩并不是对两种或以上的压缩技术进行综合使用，而是要针对压缩技术不同的技术优缺点，从扬长补短的角度出发实现技术联用。

4 结束语

图形图像的压缩技术一直以来受到业界的广泛关注，从经典的压缩方法发展到现代的压缩技术，之间出现了许多不同原理、不同效果的图形图像压缩技术。不论是经典压缩技术中的LZW编码压缩，还是霍夫曼编码压缩，在实际运用中存在一定的缺陷和不足之处。现代出现了小波变换压缩、分形编码压缩、离散余弦压缩等技术，在压缩效果上实现了大幅提升，但是还是存在一定的不足之处。因此，又提出了复合压缩的思想，将多种不同的技术进行综合使用，最大程度提升图形图像的压缩效果。所以，为了推动图形图像压缩技术的进一步发展，需要明确当前的技术原理和特点，在此基础上对现有技术进行创新，逐步提升图形图像压缩技术水平。

参考文献：

[1] 吴嵩. 基于FH8735的高分辨率图形图像压缩技术[J]. 电子技术， 2012（39）.

[2] 施耀. 计算机的图形图像及其压缩[J]. 信息技术与信息化， 2015（6）.

[3] 陈炳权， 刘宏立， 孟凡斌. 数字图像处理技术的现状及其发展方向[J]. 吉首大学学报（自然科学版）， 2009（30）.

[4] 李翠芳， 赵建荣， 侯晓荣. 基于图形矢量模式的图像几何信息压缩方法[J].计算机系统应用， 2009（12）.

[5] 林涵. 多媒体课件图像处理和图形加工技术[J]. 电脑知识与技术， 2009（35）.

[6] 嵇海波， 王凯. 小波变换技术在图像压缩领域的运用[J]. 辽宁师专学报（自然科学版）， 2011（13）.