火灾条件下混凝土箱梁梁端预应力衰变规律

张岗++刘天龙++施颖++宣纪明

摘要：针对火灾下混凝土梁桥截面损伤所导致的梁端预应力损失问题，研究了火灾高温传导模式和热传导混合边界条件，设定了预应力混凝土箱梁的火灾场景，给出了混凝土高温强度与刚度的衰减模型和烧损层计算方法；采用热力耦合计算方法和子模型分析方法计算了不同火灾场景中混凝土箱梁梁端区域钢束预应力时程变化曲线；通过工程实例分析了混凝土箱梁梁端截面不同钢束预应力的时变状态，揭示了火灾条件下混凝土箱梁梁端预应力衰变规律；通过曲线的最优与最差拟合及比较分析，提出了混凝土箱梁梁端预应力衰变计算公式。结果表明：处于箱梁梁端腹板上部的钢束预应力变化趋势受梁底部火灾面积的影响，梁底部受火面积较小时，随延火时间的增加逐渐增大，增加趋势平缓，梁底部受火面积增大时，随延火时间的增加平缓衰减；处于箱梁梁端腹板中部的钢束预应力随延火时间的增加始终呈减小趋势，处于腹板下部的钢束预应力随延火时间的增加下降幅度较大，延火至120 min时梁端钢束预应力的衰减终值介于常温下初值的94%～96%；提出的混凝土箱梁梁端预应力衰变计算公式简洁，可为类似预应力混凝土箱梁端部结构的抗火设计提供基础数据。

关键词：桥梁工程；混凝土箱梁；有限元法；预应力；火灾条件；高温

中图分类号：U448.213 文献标志码：A

0 引 言

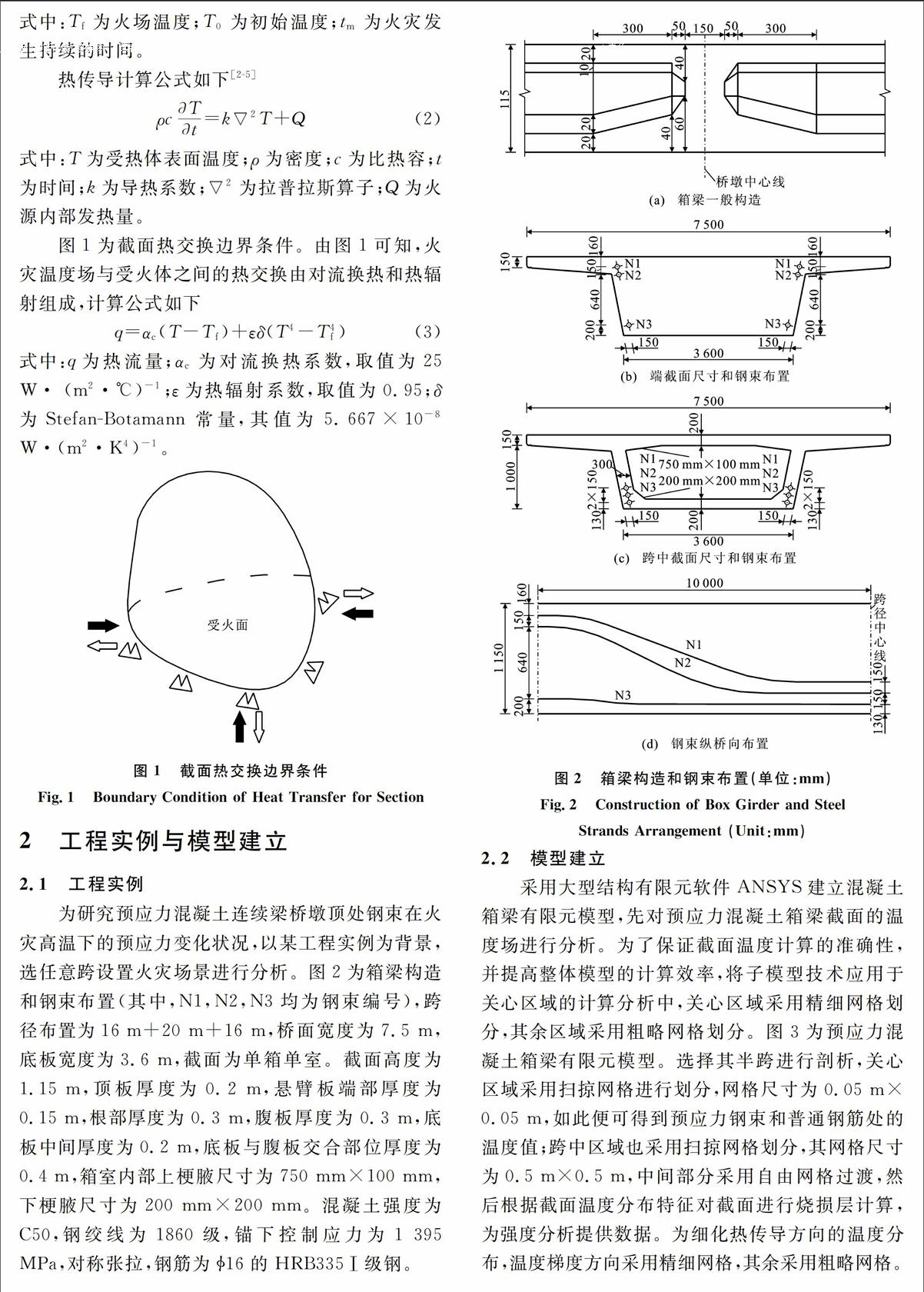
预应力混凝土桥梁遭遇火灾受损后导致截面不同部位钢束中有效预应力变异，严重影响结构应力的正常分布，威胁预应力混凝土桥梁的安全性能，因此预应力混凝土桥梁的抗火性能受到学者的重点关注，尤其是火灾高温下混凝土桥梁的预应力衰变需要进一步研究[1]。混凝土箱梁墩顶反弯处的预应力储备值对整座桥梁抗力性能至关重要，相关调研资料显示，预应力桥梁下部受火后，由于结构性能的变化致使梁端墩顶处预应力管道附近的混凝土易爆裂，周围混凝土大面积剥落，所以有必要对火灾下混凝土箱梁梁端墩顶反弯处钢束预应力变化趋势进行深入研究。目前，各国学者的研究大都集中在预应力混凝土梁桥的抗火性能，实现其准确的灾后评价及抗火设计。Garlock等[2]总结了近年来美国桥梁火灾的特点，分析了桥梁火灾的特性，并通过实例给出了桥梁火灾后安全性能的评价方法和策略；Franssen等[34]均采用数值分析方法对结构的抗火性能进行了分析，给出了较好的非线性迭代计算方法；在钢结构和混凝土结构的抗火设计方面，国外已有多部规范给出了丰富的材料高温特性，并提出了预制预应力混凝土的抗火设计方法[56]；Kodur等[78]总结了先前规范中有关桥梁抗火设计方面的严重不足，调查了美国等国家桥梁火灾发生的原因，研究了决定桥梁耐火性能的几个主要内部参数，给出了不同重要性的桥梁安全评价方法。张昊宇等[9]通过对1860级低松弛钢绞线高温下的试验研究，提出了高温下1860级钢绞线中钢丝的多种力学性能计算公式；周焕廷等[10]通过试验得到了钢绞线高温下的应力应变关系、屈服强度、抗拉强度及弹性模量计算数据；侯炜[11]通过几组试验测试了火灾高温下预应力模型梁的锚下应力变化。张岗等[1216]分析了混凝土高温传导及层剥机理，提出了火灾高温下预应力混凝土桥梁结构的非线性分析方法，研究了火灾下预应力混凝土薄腹梁的刚度衰变和支点钢束的预应力衰变速率，朱建明等[17]给出了单面受火时构件等效刚度估算方法。虽然各国学者对预应力混凝土桥梁的材料高温力学性能及结构力学性能进行了许多研究工作，但对火灾高温下预应力混凝土桥梁的预应力损失未做深入研究，其火灾高温下有效预应力目前尚不明确。本文考虑混凝土材料强度和刚度损失分层折减，在箱梁支点钢束模拟方法和预应力衰变率等[1516]相关研究基础上分析火灾条件下箱梁梁端预应力的衰变规律，可为预应力桥梁抗火实用设计方法提供依据。

4 预应力计算

图6为各计算工况下预应力时程曲线。由图6可知：当混凝土箱梁底板下部受火时，处于梁端腹板上部的钢束预应力随延火时间的增加逐渐增大，但增大幅度较小，考虑强度减损情况下，预应力由延火初时的1 030 MPa增加到延火120 min的1 032 MPa，考虑刚度减损情况下，预应力由延火初时的1 030 MPa增加到延火120 min的1 033 MPa；处于梁端腹板中部的钢束预应力随延火时间的增加逐渐减小，但衰变趋势较缓，考虑强度和刚度减损情况下，预应力由延火初时的1 017 MPa分别衰减到延火120 min的1 014，1 013 MPa；处于梁端腹板下部的钢束预应力随延火时间的增加急速减小，由延火初始的1 038 MPa衰减到延火120 min的999 MPa，大约为初值的96%。

由图6还可知，不同火灾模式下，基于强度减损和刚度减损的梁端部钢束预应力变化趋势大致相同，当截面下部受火面积增大时，处于腹板上部的梁端预应力从增加趋势逐渐变为衰减趋势，变化幅度较小，腹板和底板受火对有效预应力的影响明显，延火120 min时其可衰减至常温值的94%。5 拟合公式

图7为梁端预应力拟合曲线对比。由图7可知，二次多项式在设定的延火区间内完全逼近预应力的变化趋势，线性函数拟合效果相对较差，则拟设梁端墩顶处预应力与延火时间之间的变化关系呈二次曲线变化，可得如下计算公式

式中：Pa为梁端部墩顶处预应力；n1，n2，n3均为相关系数。

表3为相关系数取值。由表3可知，相关系数包括强度折减和刚度折减2种工况，采用ORIGINLAB拟合的各参数下公式的判定系数R2≥0.997。6 结 语

（1）针对火灾情况下混凝土箱梁端部钢束预应力损失所导致的高温连续破坏效应，设定了梁体下部发生火灾的4种火灾场景，给出了温度场计算的混凝土边界模型和热力耦合全过程分析方法，提出了混凝土高温下强度与刚度累积换算计算公式，同时基于火灾混凝土强度和刚度减损计算了混凝土箱梁梁端钢束预应力全过程变化。

（2）梁底部受火面积较小时，处于箱梁梁端腹板上部的钢束预应力随延火时间的增加逐渐增大，增加趋势平缓，梁底部受火面积增大时，处于箱梁梁端腹板上部的钢束预应力随延火时间的增加逐渐减小，衰减趋势平缓；所有火灾模式下，处于箱梁梁端腹板中部的钢束预应力随延火时间的增加逐渐减小，趋势平缓，处于腹板下部的钢束预应力随延火时间的增加下降幅度较大，延火至120 min时钢束预应力的衰减终值为常温下初值的94%～96%。

（3）通过拟合曲线比较，提出了混凝土箱梁梁端锚部钢束预应力时程衰变计算公式，揭示了基于强度和刚度减损下的混凝土箱梁梁端预应力衰变规律；本文提出的公式简洁，计算方便，可为类似预应力混凝土箱梁结构的墩顶反弯处抗火设计提供数据。

参考文献：

References：

[1] 《中国公路学报》编辑部.中国桥梁工程学术研究综述·2014[J].中国公路学报，2014，27（5）：196.

Editorial Department of China Journal of Highway and Transport.Review on Chinas Bridge Engineering Research：2014[J].China Journal of Highway and Transport，2014，27（5）：196.

[2]GARLOCK M， PAYAZAFORTEZA I， KODUR V K R，et al.Fire Hazard in Bridges：Review，Assessment and Repair Strategies[J].Engineering Structures，2012，35：8998.

[3]FRANSSEN J M.SAFIR：A Thermal/Structural Program for Modeling Structures Under Fire[J].Engineering Journal，2005，42（3）：143158.

[4]CAPUA D D，MARY A R.Nonlinear Analysis of Reinforced Concrete Crosssections Exposed to Fire[J].Fire Safety Journal，2007，42（2）：139149.

[5]EN 199112：2002，Eurocode 1：Actions on Structures.Part 1.2：General Action — Action on Structures Exposed to Fire[S].

[6]EN 199212：2004，Eurocode 2：Design of Concrete Structures.Part 1.2：General Rules — Structural Fire Design[S].

[7]KODUR V K R，NASER M Z.Importance Factor for Design of Bridges Against Fire Hazard[J].Engineering Structure，2013，54：207220.

[8]AZIZ E，KODUR V K R.An Approach for Evaluating the Residual Strength of Fire Exposed Bridge Girders[J].Journal of Constructional Steel Research，2013，88：3442.

[9]张昊宇，郑文忠.1860级低松弛钢绞线高温下力学性能[J].哈尔滨工业大学学报，2007，39（6）：861865.

ZHANG Haoyu，ZHENG Wenzhong.Mechanical Property of Steel Strand at High Temperature[J].Journal of Harbin Institute of Technology，2007，39（6）：861865.

[10]周焕廷，李国强，蒋首超.高温下钢绞线材料力学性能的试验研究[J].四川大学学报：工程科学版，2008，40（5）：106110.

ZHOU Huanting，LI Guoqiang，JIANG Shouchao.Experimental Studies on the Properties of Steel Strand at Elevated Temperatures[J].Journal of Sichuan University：Engineering Science Edition，2008，40（5）：106110.

[11]侯 炜.预应力混凝土箱梁结构抗火性能研究[D].西安：长安大学，2014.

HOU Wei.Study on the Performance of Concrete Box Girder of PSC Structure in Fire[D].Xian：Changan University，2014.

[12]张 岗，贺拴海，刘 扬，等.火灾全程预应力混凝土T梁桥刚度衰变[J].长安大学学报：自然科学版，2016，36（1）：5157.

ZHANG Gang，HE Shuanhai，LIU Yang，et al.Decay of Rigidity for Prestressed Concrete Tshaped Girder Bridge Exposed to Fire[J].Journal of Changan University：Natural Science Edition，2016，36（1）：5157.

[13]张 岗，贺拴海.焰流效应下混凝土空心薄壁墩热力耦合形差与层剥分析[J].中国公路学报，2014，27（11）：4654.

ZHANG Gang，HE Shuanhai.Thermodynamic Coupled Deformation Difference and Layering Stripping Analysis for Concrete Hollow Thinwalled Pier Affected by Flame Fluid[J].China Journal of Highway and Transport，2014，27（11）：4654.

[14]张 岗，姜长安，刘 扬，等.单侧火灾下预应力混凝土多梁肋T型结构翘曲分析[J].建筑科学与工程学报，2015，32（2）：5257.

ZHANG Gang，JIANG Changan，LIU Yang，et al.Analysis of Buckling for Prestressed Concrete Multibeam Tshaped Structure Exposed to Unilateral Fire[J].Journal of Architecture and Civil Engineering，2015，32（2）：5257.

[15]张 岗，刘天龙，王翠娟，等.强度减损下混凝土箱梁预应力火灾高温损失分析[J].解放军理工大学学报：自然科学版，2015，16（4）：345352.

ZHANG Gang，LIU Tianlong，WANG Cuijuan，et al.Prestress Loss of Concrete Bridge with Box Girder Based on Strength Reduction Exposed to Fire[J].Journal of PLA University of Science and Technology：Natural Science Edition，2015，16（4）：345352.

[16]张 岗，施 颖，宣纪明，等.混凝土连续箱梁支点处钢束预应力高温衰变研究[J].桥梁建设，2016，46（1）：7680.

ZHANG Gang，SHI Ying，XUAN Jiming，et al.Study of Prestress Decay of Steel Strands in PC Continuous Box Beam at Support Under High Temperature[J].Bridge Construction，2016，46（1）：7680.

[17]朱建明，王晓纯，魏 东，等.火灾后混凝土构件的剩余刚度估计[J].工程力学，2011，28（8）：193197，207.

ZHU Jianming，WANG Xiaochun，WEI Dong，et al.Estimation of the Residual Stiffnesses of Firedamaged Concrete Members[J].Engineering Mechanics，2011，28（8）：193197，207.