目标跟踪的转换量测卡尔曼滤波算法性能分析

贺宏洲,秦玉峰,杨渝波,杨立明,雷　静

(空间电子信息技术研究院 测控技术室,陕西 西安　710000)



目标跟踪的转换量测卡尔曼滤波算法性能分析

贺宏洲,秦玉峰,杨渝波,杨立明,雷静

(空间电子信息技术研究院 测控技术室,陕西 西安710000)

摘要各种转换量测算法均是基于不同假设条件下对最优解的近似,不同的应用环境可能造成算法完全迥异的性能表现,因此有必要对各种不同的转换量测算法进行统一的分析和比较。文中讨论分析了几种典型的转换量测算法,并通过仿真分析比较了它们在不同环境下的跟踪性能,可信性和运算复杂度。最佳线性无偏估计算法的平均归一化估计误差平方约等于1,是最小均方误差意义下的理论最优估计,其跟踪性能最优。

关键词目标跟踪;卡尔曼滤波;转换量测;条件均值和协方差;性能分析

在航天器目标跟踪系统中,量测一般是在极(球)坐标系下获得,但目标状态方程通常是在直角坐标系下描述,这就涉及利用极(球)坐标下的量测实现直角坐标系下目标跟踪问题,即非线性系统下目标跟踪问题。通常采用两种方法:(1)采用扩展卡尔曼滤波(EKF)算法,形成所谓混合坐标滤波器;(2)将极坐标系量测转换到直角坐标系下,再用转换量测算法。

传统转换量测算法通过一阶泰勒级数展开近似转换后直角坐标系下的量测误差,在远距离角度误差较大时性能明显下降。第一个针对二维情况去偏转换算法(DCMKF)由Lerro[1]等于1993年提出,后由Suchomski等扩展到3维情况。它采用加性偏差补偿措施,先求得转换量测误差基于真实极坐标位置(距离,方位角)下条件均值和方差,因实际真实位置不可获得,要再基于量测信息对上述均值和方差求条件期望来获得近似解。实际由于这种双重条件均值,算法[1]并不是真正无偏[2-3]。1998年Mo等[2,4]提出一种适用于非高斯噪声的真正无偏转换量测算法(UCMKF),认为转换量测误差的偏差本质上是乘性的。先在转换量测的基础上除去乘性偏差补偿因子可获无偏转换量测,后在量测已知条件下求得无偏转换量测协方差。但文献[5]指出该协方差计算存在前后不一致,并给出修正后转换量测算法。

自DCMKF和UCMKF算法提出后,转换量测算法得到广泛研究。Spitzmiller[6]对DCMKF算法进行适当补充并开展更深入研究。文献[3]一定程度总结了当时现有转换量测算法,只是用均方误差代替协方差,将去偏转换算法分为3类:量测固定目标真实位置变化(Fixed Measurement),目标真实位置固定量测变化(Fixed Target Truth),估计值固定量测和目标真实位置均变化(Fixed Independent Estimate)。以上多数算法转换量测误差的条件均值和协方差均是基于量测条件下求得,但特别是跟踪阶段,状态估计精度要高于量测信息,基于状态估计求条件均值可能是更好选择。文献[3]的Fixed Independent Estimate是最早基于估计的转换量测算法,但给出假设相对简单。文献[6～8]在此方向做出更深入研究。但以上算法都存在根本缺陷:转换后量测噪声与状态相关,协方差在当前量测的基础上估计得到,观测噪声不再是白噪声。文献[9] 针对上述缺点做了部分改进。但文献[10]指出一旦预测量测和量测残差的协方差已知,卡尔曼滤波不再需要知道转换量测误差的均值和方差。它提出利用最小线性无偏估计(BLUE)滤波方法来处理非线性量测,得到理论最优算法。Park等[11]也提出基于预测条件求转换量测误差均值和协方差的思想,并开发一种类EKF形式滤波算法,它仍假定真实状态是固定非随机,与卡尔曼滤波算法的假定实际是相矛盾,理论上性能不会超过BLUE算法。

实际以上转换量测算法均是基于不同假设条件下对最优解的近似,不同应用环境可能造成算法完全迥异的性能表现。有必要对各种不同转换量测算法进行统一分析和比较,为后续相关研究和应用提供理论参考。文献[12]对当时流行的各种转换量测算法核心思想进行总结和分析,但没给出具体仿真比较。本文针对距离-方位角-俯仰角形式的量测系统,讨论5种典型转换量测算法,通过设定不同仿真环境,对各算法性能优劣展开分析和比较。BLUE算法是最小均方误差意义下的理论最优估计,顺序处理量测的类EKF算法与BLUE算法的性能接近,其它转换量测算法的性能优劣与跟踪环境有关,视情况而定。

1问题描述

考虑三维情况下的跟踪问题,目标的状态方程描述为

(1)

(2)

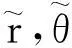
xm=rmZEEθmZEEφm,ym=rmsinθmZEEφm,zm=rmsinφm

(3)

(x,y,z)是目标的真实位置,可得到转换量测误差为

(4)

显然,转换量测误差与量测相关,非高斯,各坐标间耦合而且均值不再为零。因此转换量测实际是有偏的,需要计算转换量测误差的均值和相应的协方差,然后去偏,最后采用线性滤波算法(卡尔曼滤波),只是不同的转换算法计算均值和协方差的方法不同。

2典型转换量测算法

2.1加性去偏转换量测算法

2.2乘性去偏转换量测算法

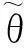
(6)

2.3基于量测的转换量测算法

此算法也称为“固定量测(Fixed Measurement)算法”[3],转换量测误差的均值和协方差计算均是直接基于量测条件下求得的。

对式(4)基于量测求条件期望得到均值

(7)

2.4基于估计的转换量测算法

文献[1]中曾指出当位置估计的精度高于量测时,应使用估计值作为已知条件来求转换量测误差的条件期望和方差,但并没给出具体统计结果和分析,文献[7]推出一种新的基于位置估计的转换量测算法。

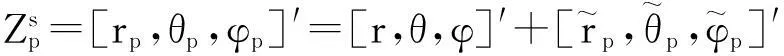
(8)

则转换量测误差的均值可以表示为

(9)

其中

(10)

2.5最佳线性无偏估计滤波

先假定Zk和Xk分别为k时刻的量测和状态,Zk-1表示k时刻之前的所有量测。准递归形式的最优线性无偏状态估计可表示为

(11)

其中

(12)

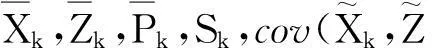
对于转换后的量测,由文献[10]中的引理1、引理2和一系列运算及推导得到

(13)

3性能分析

3.1仿真条件

为比较上述几种转换量测算法的跟踪性能,设计了一个三维匀速运动目标的跟踪问题并给出了2种不同情况下的仿真结果。目标初始位置为(150,120,5) km,速度为(100,700,400) M/s,过程噪声q=0.01 M/s2。仿真条件1:距离,方位角和俯仰角的量测误差标准差分别为100 M,5°和5°。仿真条件2:距离,方位角和俯仰角的量测误差标准差分别为30 M,1.5°和1.5°。雷达的采样周期为1 s,整个跟踪过程持续200 s。蒙特卡洛仿真次数为100次。

本文采用位置均方根误差(RMSE)来反映算法的跟踪精度,平均归一化估计误差的平方(ANEES)来反映算法的可信性。ANEES的定义如下

(14)

3.2仿真结果

对于仿真条件2,各个算法的位置RMSE和ANEES分别如图3和图4所示。当量测误差减小时,各个算法的跟踪精度和可信性都显著提高,BLUE最优,DCMKF最差。此时由于横向距离误差减小,DCMKF的跟踪精度接近于UCMKF,ECKF的跟踪精度则高于MCKF算法。

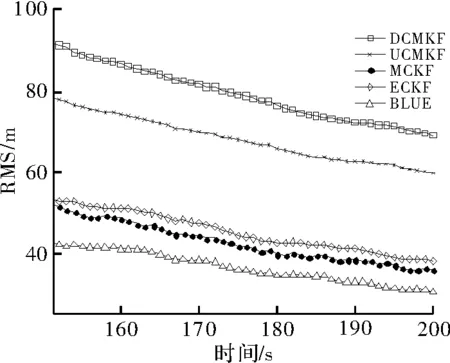
图1　条件1时各算法的位置均方根误差

图2　条件1时各算法的ANEES曲线

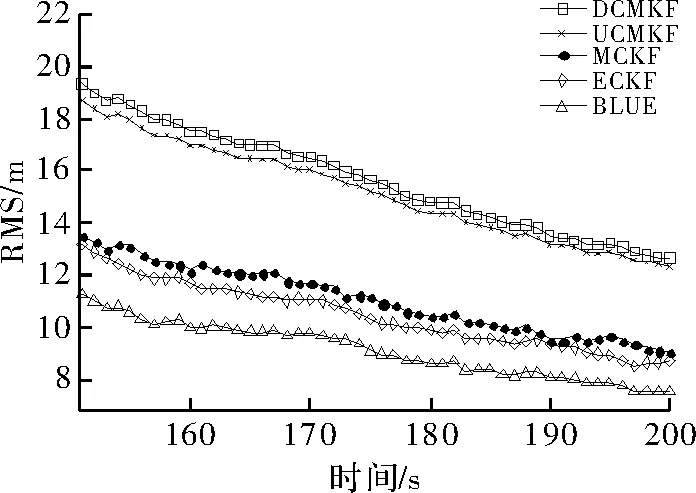
图3　条件2时各算法的位置均方根误差

图4　条件2时各算法的ANEES曲线

关于运算复杂度,表1给出各个算法运行一次仿真所需时间。可见MCKF最快,而无味变换的使用导致ECKF所需计算时间最长。BLUE的处理时间略高于DCMKF和UCMKF。可看到,BLUE的跟踪性能最优,而运算时间却没显著增加。

表1　各个算法的CPU运行时间对比　/s

4结束语

转换量测算法是在航天器目标跟踪领域处理非线性量测的一种有效方法。本文回顾了转换量测算法的发展历程,讨论几种典型的转换量测算法的核心思想,并通过设定不同仿真环境分析比较了它们的跟踪性能,可信性和运算复杂度。最佳线性无偏估计(BLUE)算法是最小均方误差意义下的理论最优估计,其跟踪性能和可信性都最优,而运算时间却没显著增加。综合比较可见BLUE算法是最优的。MCKF和ECKF跟踪性能差于BLUE算法,UCMKF再次,DCMKF跟踪性能最差。由于使用无味变换,ECKF运算最慢,而BLUE和UCMKF运算速度相当,MCKF最快。

目前转换量测算法需转换量测误差均值和方差的清晰表达式,这使它的应用有一定局限性,因此很多其他的处理非线性量测的方法如无味卡尔曼滤波,粒子滤波等得到了广泛研究,需根据具体的研究问题选择最合适滤波方法。

参考文献

[1]Lerro D,Bar Shalom Y.Tracking with debiased consistent converted measurements versus EKF[J].IEEE Transactions on Aerospace and Electronic Systems,1993,29(3):1015-1022.

[2]Mo L,Song X,Zhou Y,et al.Unbiased converted measurements for tracking[J].IEEE Transactions on Aerospace and Electronic Systems,1998,34(3):1023-1026.

[3]Miller M,Drummond O.Coordinate transformation bias in target tracking[C].Denver,CO:Proceeding 1999 SPIE Conference on Signal and Data Processing of Small Targets,1999.

[4]Mo L,Song X,Zhou Y,et al.Alternative unbiased consistent converted measurements for target tracking[C].Orlando,FL:Proceedings of SPIE:Acquisition,Tracking,and Pointing XI,1997:.

[5]Duan Z,Li X R.Comments on “unbiased converted measurements for tracking”[J].IEEE Transactions on Aerospace and Electronic Systems,2004,40(4):1374-1377.

[6]Spitzmiller J N,Adhami R R.New investigative findings from the debiased converted-measurement kalman filter[J].Intelligent Information Management,2010(2):431-436.

[7]Spitzmiller J N,Adhami R R.Tracking with spherical-estimate-conditioned debiased converted measurements[C].Washington DC:2010 IEEE Radar Conference,2010.

[8]Tian Junlin,Fu Chengyu,Tang Tao.An improved evaluation method for converted statistics in converted measurement kalman filtering algorithm[J].Opto-Electronic Engineering,2011,38(8):20-26.

[9]Wei Mei,Bar-shalom Y.Unbiased kalman filter using converted measurements:revisit[C].San Diego,CA:Signal and Data Processing of Small Targets,2009.

[10]Zhao Z,Li X R,Jilkov V P.Best linear unbiased filtering with nonlinear measurements for target tracking[J].IEEE Transactions on Aerospace and Electronic Systems,2004,40(4):1324-1336.

[11]Park S E,Lee J G.Improved kalman filter design for three-dimensional radar tracking[J].IEEE Transactions on Aerospace and Electronic Systems,2001,37(2):727-739.

[12]Li X R,Jilkov V P.A survey of maneuvering target tracking—part III:measurement models[C].San Diego,CA,USA:Proceedings of SPIE Conference on Signal and Data Processing of Small Targets,2001.

Analysis of the Performance of Converted MeasurementKalman Filter Algorithms for Target Tracking

HE Hongzhou,QIN Yufeng,YANG Yubo,YANG Liming,LEI Jing

(Laboratory of TT&C Technology,CAST-Xi’an Institute of Space Radio Technology,Xi’an 710000,China)

AbstractThe converted algorithms are approximations of the optimal solution based on different assumptions,leading distinct performance in different applications,thus it is necessary to uniformly compare and analyze the performance of different converted algorithms.In this paper,the typical converted measurement algorithms are demonstrated.Their performances in different scenarios are evaluated by simulations in terms of tracking accuracy,credibility and computation complexity.The averaged normalized estimation error squared of the best linear unbiased estimate (BLUE) is approximately equals to 1,which is theoretically optimal in the sense of minimum mean square error with superior tracking performance to other filters.

Keywordstarget tracking;Kaman filter;converted measurement;conditional mean and covariance;performance analysis

中图分类号TN953

文献标识码A

文章编号1007-7820(2016)05-112-05