全变分信号去噪的最佳参数选择方法

胡月娇,许成哲（延边大学 计算机科学与技术学科,吉林 延吉 133002）



全变分信号去噪的最佳参数选择方法

胡月娇,许成哲
（延边大学 计算机科学与技术学科,吉林 延吉 133002）

摘 要：基于现有的全变分信号去噪过程中依靠经验选择参数使得去噪效果精确度低的问题，本文提出一种新颖的全变分信号去噪的最佳参数选择方法，将粒子群优化算法（PSO，Particle Swarm Optimization）运用其中，首先研究了全变分图像去噪模型，介绍标准PSO算法过程，结合粒子群优法来选择最佳参数，分析了粒子群优法选择参数的过程，实验结果显示了本文所提出的参数选择方法有效性和可靠性。

关键词：全变分；信号去噪；粒子群优化算法

0 引言

在图像获取或传输的过程中，由于受到各种因素的影响，图像不可避免地受到了噪声的污染，给后续图像处理过程带来了极大的困难。因此图像去噪是图像处理中一个重要环节，图像的噪声去除和细节保护是一对矛盾关系，图像的低通滤波在去除噪声的同时，产生图像边缘的模糊,而人对图像的高频成分是敏感的。近年来，全变分法的图像降噪技术得到了应用，我们在运用全变分模型来去噪时候会用到很多参数。而在以前的研究中，在选取这些参数的最佳数值时，通常是依赖经验来选取的。也就是依靠经验在某个数值范围中选取适当参数值，然后去尝试处理图像。参数少的话，其组合还可以罗列。而如果参数多的话，这显然是不太方便的。运用PSO来选取最佳参数正是基于这样的背景下提出的。

1 研究现状

1992年，Rudin、Osher和 Fatemi提出了一种基于全变分（TV，Total Variation ） 模型的去噪方法［1］。该方法实质上就是各向异性扩散，它能在去噪的同时很好地保持图像的边缘。由于全变分方法引入偏微分方程的各向异性扩散方程用于图像去噪，在平滑噪声的同时，可以使边缘得到保持，较好地解决了恢复图像细节和抑制噪声之间的矛盾［2］。基于偏微分方程的变分模型方法高质量的处理效果已引起国内外研究学者的广泛重视［3］。近年来又有其他研究者发现全变分模型存在的不足，提出了一种基于平滑核的广义变分模型［4］。实验结果表明，该模型对于高斯噪声污染的图像能取得良好的恢复效果，相比于全变分模型，该模型获得的去噪后的图像具有更好的客观评价指标和细节保护能力，同时还有效避免了阶梯效应［5］。Bing S提出了一种基于 范数的广义的TV 去噪模型该模型能克服假边缘的产生，且在去噪的同时保持了边缘，但该模型的峰值信噪比较低［6］。鉴于上述存在的局限，本文在前人研究变分问题直接解法的基础上，建立求解含一阶导数的变分问题优化模型，构造出了适应度函数，从而使得PSO算法成功应用到变分问题的求解当中。

2 全变分图像去噪模型

最近的研究利用Graph Laplacian，把传统的全变分（TV，Total Variation ）的局部像素联系扩展到了非局部（NL，Non-Local）联系，与之相对应的模型是NLTV（Non-Local Total Variation）模型，也称为NL-ROF模型。NLTV的定义式如下：

上式可以用Split-Bregman反复法求解，其解可以表示为如下形式：

式中，λ是Lagrangian乘数；b是Bregman参数

3 NLTV去噪模型的参数选择方法

本研究中，我们利用粒子群优化算法（PSO，Particle Swarm Optimization）选择了NLTV去噪模型的参数，粒子群优化算法的目标函数是由图像去噪之后的峰值信噪比（PSNR）来构建的。

3.1 标准PSO算法的求解步骤

算法的具体步骤［7］如下：

（1）初始化粒子群：初始化粒子群的规模，包括其位置和速度，对每个粒子，这里都是在其允许的范围内随机地产生每一维的初始位置和初始速度。

（2）适应值的计算：对于每个粒子，首先按照建立的模型构造适应度函数，计算出各个体的适应值。

（3）更新全局和局部最好粒子位置：对每个粒子，将其适应值与所经历过的最好位置（即局部最优值）进行比较。

（4）飞翔算子：搜索过程中，采用标准PSO算法的进行速度更新，从而实现整个进化过程。

（5）终止条件：设置一个最大迭代次数，当迭代次数达到最大值时结束进化，否则转步骤2继续进化。

3.2 NLTV去噪模型的参数选择方法

NLTV去噪模型的性能主要取决于尺度参数h、标量权重μ，Split-Bregman求解过程中产生的Lagrangian乘数λ和循环次数k，而去噪的性能可以用PSNR来定量分析。因此，我们可以假设图像去噪后的PSNR为NLTV模型的参数的函数：

其中，f表示函数。若视f（h， μ，λ，k）为目标函数，则可以利用PSO求解最大化PSNR的最优解（Optimal Solution），即可以选择最优的4个参数。用PSO选择最优参数的时候，位置矢量和速度矢量都是4维矢量。公式3-1中的PSNR（峰值信噪比）的定义式如下：

其中，MSE是原图像与去噪图像之间的均方误差。PSNR的单位为dB，PSNR值越大，表示图像的失真越少。

4 实验结果

如图1图像去噪效果对比所示，我们利用Babara原始图像进行了实验。首先给图像添加高斯噪声之后生成一个加噪图像，其噪音级别为0.05，然后用NLTV去噪模型对它进行去噪，图像去噪的PSNR是根据公式（3-2）计算出来的。实验中，用PSO选择了NLTV的4个参数h、μ、λ、k，这时，NLTV的检索领域大小固定为11*11，patch大小固定为5*5。对PSO参数设置如表1 所示。

表1 PSO参数设置

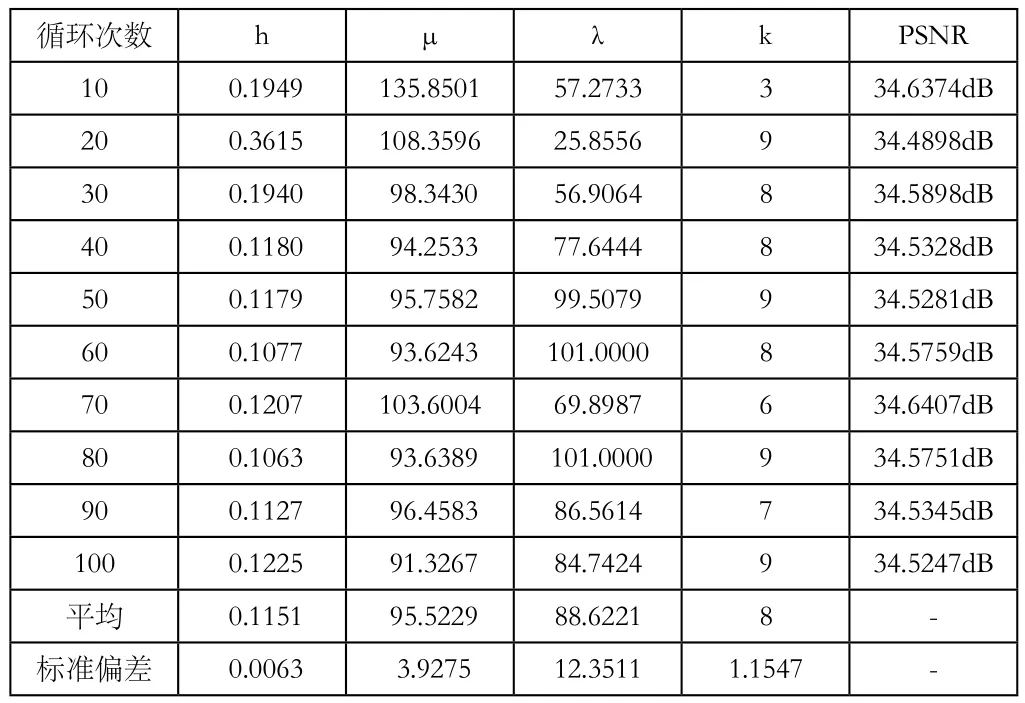
表2 用PSO选择参数的实验结果

经过多次实验得出PSO选择参数的结果如表2表示，从表中可以看出PSO的循环次数为40以上的时候4个参数值都基本上收敛，表2中的平均项和标准偏差项是循环次数为40以上的各参数的平均和对应的标准偏差。由此我们可以确定NLTV的4个参数的范围：h的范围为0.12左右；μ的范围为95.52。λ的范围为88.62左右、k的范围为8左右。

5 结论

本文将PSO算法应用到了求解变分问题的近似解当中，拓展了PSO算法的应用领域。经过以上分析，可以看出用PSO方法可以很好的得出最佳参数，且简单易行。通过文中建立的模型及数值实验结果来看，该思路是完全可行的，结果的精度也令人非常满意。对研究变分问题的直接解法具有重要的理论和实际意义。然而本文仅简单的变分问题进行了讨论，对于PSO算法在更一般的变分问题中的应用，还有待进一步的研究。

参考文献：

［1］老大中.变分法基础［M］.北京：国防工业出版社,2007：46-75.

［2］侯榆青,张欢,杨旭朗,陈燊.全变分图像复原的研究及其三种数值方法比较［D］.2008（33）：295-297.

［3］杨维,余斌霄,宋国乡.基于变分问题和广义软阈值的图像去噪［D］.2005（27）：1855-1857.

［4］王益艳.基于平滑核的广义变分去噪模型［J］.重庆师范大学学报（自然科学版）,2010（27）：59-64.

［5］陈明举,杨平先,王晶.基于正则化与保真项全变分自适应图像去噪模型［J］.重庆邮电大学学报（自然科学版）,2011（23）：621-625.

［6］谢殿广,杨进华,申琳,李培平.基于改进的自适应全变差模型的图像去噪算法［J］.长春理工大学学报（自然科学版）,2010：98-100.

［7］傅阳光,周成平,丁明跃. Convergence Analysis of Standard Particle Swarm Optimization Algorithm［J］.应用数学,2011,24（01）：187-194.

DOI：10.16640/j.cnki.37-1222/t.2016.12.127

作者简介：胡月娇（1990-），女，吉林松原人，硕士研究生，主要从事：心电信号身份识别算法。