基于改进BPSO的最小碰集搜索方法应用研究

陈 忱（中国航空综合技术研究所,北京 100028）



基于改进BPSO的最小碰集搜索方法应用研究

陈 忱
（中国航空综合技术研究所,北京 100028）

摘 要：本论文在对比分析常用最小碰集搜索方法性能优劣的基础上，提出了一种改进的离散二进制粒子群算法，并给出了该算法应用于最小碰集搜索的基本规则与流程，从最小冲突集集合簇中搜索获得全部最小碰集并做出诊断结论。随后，以卫星电源系统为应用案例，验证了该方法的性能优势、适用性以及工程实用性。

关键词：基于模型诊断；冲突集；碰集；离散二进制粒子群算法

1 引言

基于模型诊断（Model-Based Diagnosis, MBD）作为故障诊断技术的分支之一，又被称为基于“深知识”的诊断方法，它通过建立诊断对象的定性抽象模型，发挥定性分析、推理方法简单易行的优势，总结出抽象建模的基本规则，既解决了知识获取瓶颈与知识库维护困难问题，又能有效提高诊断的精确性，特别是针对具备层次性、耦合性、冗余度等特点的航空航天类电子产品，具有较高的应用价值［1］。

基于MBD的基本思想，诊断过程可分为系统建模、冲突识别与诊断生成。其中，诊断生成环节的基本任务就是完成最小碰集搜索，如何尽可能提高最小碰集搜索效率也成为了MBD技术领域的研究热点。目前，可以将最小碰集搜索算法分为三类，分别是树形搜索算法、布尔代数搜索算法，以及以遗传算法为代表的一系列人工智能方法。其中，HS-TREE、HST-TREE、BHS-TREE［2］等树形搜索算法需要建立树或者图，可能因为剪枝问题而丢失正确解，算法编程实现繁琐且计算效率差；布尔代数方法［3］在计算碰集时不需建树，不会因剪枝而丢失正确解，但需要预先存储所有碰集，通过化简得出最小碰集，在一定程度上限制了计算效率；遗传算法［4］的空间复杂性对冲突集的规模不敏感，适用于求解冲突集规模较大的情况，但只能较快计算出部分碰集，不能保证所有输出结果均为最小碰集。

鉴于此，本文设计采用离散二进制粒子群算法BPSO，将最小碰集的搜索问题转化为用0、1表示的二值空间的搜索问题，并通过对算法进行适当改进，提高原有最小碰集的搜索效率。

2 基于模型诊断MBD的基本原理

MBD的基本思想［5］是利用产品系统内部结构或行为知识完成诊断，是一套面向冲突的故障诊断推理方法，这里的冲突指的是在被诊断系统所有组成元件均正常工作的假设前提下，系统观测值与预期值之间存在差异的现象。下面，首先给出MBD方法中的几个基本概念。

定义1：待诊断系统：MBD的分析对象，采用一阶谓词逻辑语句将其抽象描述成一个三元组（SD,OBS,COMP）的形式。其中，SD是系统描述，用一阶谓词逻辑公式集合描述系统的正常结构和行为；OBS为系统观测集，由一阶谓词公式的有限集来表达；COMP表示一阶谓词逻辑的函数符号或常量集，为组成系统的元件集合，是一个有限集合。

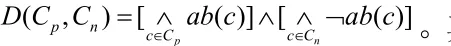
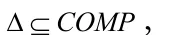
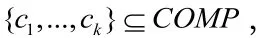
定义5：最小冲突集：当且仅当某一冲突集的任何一个非空真子集都不是冲突集时，该冲突集是最小冲突集。

定义6：碰集：给定一个集合簇（集合的集合），若一个集合与这个集合簇中的全部集合的交集均不为空集，则称该集合为此集合簇的碰集。用符号表示方法如下所示。设C是一个集合簇，C的碰集是一个集合H，H需要满足两个条件：H⊆ S∪，其中S∈ C；∀S∈ C，则H∩ S≠∅。

定义7：最小碰集：当一个碰集的任意一个非空真子集均不是碰集时，则称它为最小碰集。

在上述基本概念定义的基础上，Reiter最早提出了基于模型诊断的基本流程框架，即将诊断过程分为系统建模、冲突集识别、碰集搜索三个环节，这也是后续基于模型诊断领域研究的基础。本论文在前序研究中将这一基本流程细化如图1所示，在此重点针对其中的最小碰集识别过程进行论述。

3 基于改进BPSO的最小碰集搜索方法

3.1 基本思路

对于某一电路系统来说，最小冲突集是由系统中若干元器件组成的，其中至少有一个是故障的，才能够解释电路系统通过模型推理得到的预期结果和实际观测结果之间存在差异。本文引入BPSO算法求解最小碰集的基本思想，就是将冲突识别环节已求得的最小冲突集映射成用0、1表示的N纬二值集合， N代表元器件的规模，最小碰集的搜索问题就转化为0、1表示的二值空间搜索问题。

具体来说，本文提出的最小碰集求解问题与BPSO算法之间的对应转换关系见表1。

（1）电路系统的所有组成元器件都存在正常与故障两种状态，对应到最小冲突集映射成的N维二值集合中，每一维的值代表该维对应元器件的状态，即0表示正常，1表示故障；

（2）BPSO算法关键变量之一为粒子位置，该向量每一维的值都被限制为0或1，即表示N维二值集合中每一维对应的元器件状态是正常或故障；

表1 解最小碰集与BPSO算法的对应转换关系列表

（3）BPSO算法的另一关键变量是粒子速度，它表示位置状态改变的可能性，即粒子位置接近于1的概率，取值限定在［0,1］之间；

（4）碰集粒子是BPSO算法每次迭代获得的中间结果，每个碰集粒子对应一个碰集，即该行向量中值为1的元素对应的元器件就是该粒子代表的碰集组成元素，需要进一步缩小获得最小碰集粒子；

（5）BPSO算法最终获得多个最小碰集粒子，由碰集粒子删除超集后得到，每个粒子对应着一个最小碰集，即该行向量中值为1的元素对应的元器件就是该粒子代表的最小碰集组成元素。

通过上述对应转换关系，可以实现用二进制编码的方式来表示N维二值空间中的某一维是否被选择进入最小碰集集合中，值为1即表示该维对应的元器件被选入最小碰集中，利用BPSO算法获得的所有最小碰集即为最终输出的诊断结论。

3.2 计算公式与规则的改造

在实际求解最小碰集的过程中，原始BPSO算法的计算公式不再适用于最小碰集搜索问题中的集合运算，需要重新定义计算规则。因此，本文针对求解最小碰集这一最终目标，对算法执行过程中涉及到的相关公式做出适当的调整与改造，并重新定义了二值向量/矩阵运算时的规则。

3.2.1 粒子速度更新公式

粒子速度更新公式与标准BPSO算法中的粒子速度更新公式保持一致。但在利用该公式进行迭代计算时，粒子速度的物理含义是状态变化概率，经过上述公式中的乘法、加法运算后，更新后的粒子速度值仍应限定在［0,1］之间；同时，pid-xid（t）与pgd-xid（t）均为矩阵行向量之间的运算，且行向量元素均为0或1，则可能会出现元素“0-1=?”的情况。因此，需要对可能出现的运算设定合适的计算规则。首先，将本文中设计采用的BPSO算法中粒子速度更新的操作分解成如图2所示的子过程，并将粒子速度更新过程中出现的计算类型分为四种情况，并分别给出计算规则。

①系数×速度。给定一系数c（c＞0）和一速度向量（概率向量）V，两者乘积将定义为cV，具体形式如下：

其中pi（i=1,2,…,n）为原始速度向量中的概率，pi’为速度向量乘以系数后向量中的概率值。可以看出“系数×速度=系数×概率”，其结果为“概率”。

②位置-位置。“位置-位置”计算对应于传统的集合减法操作定义，给定两个粒子位置向量A与B，A-B具体定义如下。其中，A与B的元素为xi、yi（i=1,2,…,n），取值均为0或1。

根据本条规则可知，zi=xi-yi的所有可能情况见表2，“位置-位置”计算结果仍为“位置”。

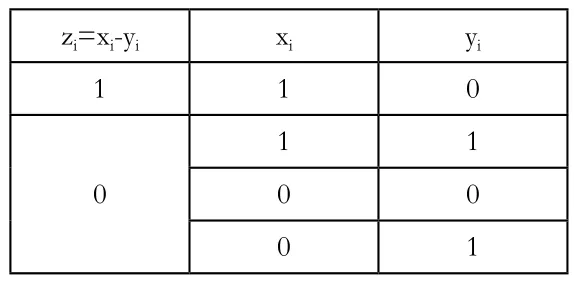
表2 “位置位置”计算规则

③系数×（位置-位置）。“位置-位置”的结果仍是位置，则要进行“系数×（位置-位置）”，就需要定义“系数×位置”的计算规则。给定一个系数c（c＞0）和一个位置向量A，两者的乘积将定义为cA，具体形式如下。

通过上述计算，实际上是将位置这一向量通过系数相乘后，转化为一概率向量，即可以与速度向量（概率向量）进行加法运算，如下一条规则所示。

④概率+概率。给定两个概率向量V1与V2，两个向量的组成元素均为概率，即每个元素取值范围都在［0,1］之间，两者相加为V1+V2，具体形式如下，其中（i=1,2,…,n）。

此条规则实际上是用于三个概率向量相加，即ωvid（t）的计算结果为第一个概率向量，以c1r1（pid-xid（t））的计算结果是第二个，c2r2（pid-xid（t））的计算结果是第三个。通过规定概率相加的结果是取两个概率的最大值，可以使最终计算结果的值始终被限定在［0,1］之间。可以看出，“概率+概率”的结果仍为概率，即更新后获得的新的粒子速度向量。

3.2.2 粒子位置更新公式

利用BPSO算法进行最小碰集求解，需对粒子位置更新公式做出相应的调整，最终结果如下。如果t+1次迭代的粒子速度大于t次迭代时的粒子速度，t+1时刻的粒子位置更新为0，否则更新为1。

3.2.3 适应度函数计算公式

在BPSO算法中采用适应度函数来评价各个粒子位置的优劣以及粒子群位置的优劣，从而实现引导粒子群体向最优方向寻优（即更新粒子位置和粒子速度）。由此可见，适应度函数直接影响着通过BPSO算法求出的最小碰集的正确性，也影响着算法的搜索效率，即适应度函数在利用BPSO算法搜索最小碰集过程中起着至关重要的作用。

若直接将传统BPSO算法应用于最小碰集搜索问题，则仅针对粒子群整体进行寻优，即算法的适应度函数仅用于评价整个粒子群。为了进一步提高搜索效率，本论文采用粒子群整体寻优与单个粒子寻优相结合的方法，即分别制定粒子群和单个粒子的适应度函数公式如下。

式中，P为粒子群种群规模，即设定的粒子数量；h为当前粒子群中不同的碰集粒子个数；m为最小冲突集集合簇中最小冲突集个数；x为单个粒子i对应的二值集合与最小冲突集有交集的个数。

由于本文采用BPSO算法的目的是搜索最小碰集，碰集与所有最小冲突集都有交集，结合适应度函数公式可以看出，单个粒子与粒子群的适应度值均是越大越好；同时，由于h的最大值只能为P，x的最大值只能为m，所以上述适应度函数的最大值均为1；另外，当fpi=1时，说明x=m，即该粒子i为碰集粒子，对应一个碰集。

3.3 算法流程

本文将上述利用改进BPSO算法搜索最小碰集的基本思路转化为具体的实施流程，见图3。

步骤一：将已获得的最小冲突集映射到二值空间中，设此二值空间维数为N。

步骤二：粒子群及相关参数初始化设定。设定种群规模为P；初始化粒子群为一个P×N维的随机二值矩阵作为粒子群初始位置x（1）；初始化一个P×N维的随机矩阵作为粒子群初始速度v（1），所有元素取值均在［0,1］之间；设置惯性权重ω、学习因子c1和c2、最大迭代次数Tmax；令迭代次数t=1；初始化一个N维矩阵Hs存储搜索出的碰集粒子。

步骤三：计算每个粒子的适应度函数值fpi（i=1,2,…,P）以及粒子群适应度值fg。

步骤四：若当前迭代次数t=1？若t=1，执行步骤五；若1＜t＜Tmax，执行步骤六。步骤五：迭代次数t=1时，更新个体极值向量与群体极值向量。对于个体：以初始状态粒子适应度值和粒子位置作为个体适应度极值fpbesti（i=1,2,…,P）以及个体极值向量pi（i=1,2,…,P）。

对于群体：以初始状态群体适应度值作为群体适应度极值fgbest，初始状态下适应度函数值fpi最大的粒子位置作为群体极值向量pg。

步骤六：迭代次数1＜t≤Tmax时，更新个体极值向量与群体极值向量。

对于个体：若fpi≥fpbesti，令fpbesti=fpi，同时令pi=i（t），即将粒子个体极值向量更新为当前粒子；若fpi＜fpbesti，fpbesti与pi均保持不变。

对于群体：若fg≥fgbest，更新群体适应度极值fgbest=fg，更新群体极值向量pg=i（t），该粒子i（t）需要与现有Hs矩阵中存储的碰集粒子不同，若相同则不更新pg；若fg＜fgbest，fgbest与pg均保持不变。

步骤七：根据fpi=1的原则，找出当前粒子群中的碰集粒子，将其中与现有Hs矩阵中存储的碰集粒子不同的粒子存入Hs中。

步骤八：按照粒子位置、速度更新公式与相关计算规则，更新粒子群位置与速度，生成用于下一次迭代的新粒子群位置x（t+1）与粒子群速度v（t+1），t为当前的迭代次数。

步骤九：若当前迭代次数t=Tmax，执行步骤十；否则令t=t+1，返回步骤三。

步骤十：当迭代完成后，根据当前矩阵Hs，删除其中的超集粒子，剩余的即为最小碰集粒子组成矩阵Hs’，这些粒子中元素值为1的维度所对应的元器件所组成的集合即为最小碰集，最小碰集粒子的个数即为最小碰集的个数。

3.4 算法性能比较

将本文提出的改进BPSO算法（针对单个粒子以及粒子群整体共同寻优）与传统的BPSO算法（仅针对粒子群进行寻优）分别用于解决同样的最小碰集搜索问题，同时也经典树形搜索算法HS-Tree、布尔代数搜索算法Boolean、遗传算法GA的诊断效果进行比较，利用问题规模与搜索时间之间的关系比较上述算法的搜索效率。

引用姜云飞、林笠学者在文献［3］中的例子进行算法对比验证，已知如下三个条件：

假设最小冲突集集合簇中包含10个最小冲突集，即n=10；

各个冲突集分别为｛1,2,…,m｝，｛2,3,…,m+1｝，…，｛n,m+1,…,n+m-1｝；

问题规模P=n+m-1分别取10，20，30，…，90，即m分别取1，11，…，81。

利用上述五种不同方法搜索最小碰集，得到的实验最终对比结果见图4，各算法性能对比分析的具体情况总结如下：

（1）传统的HS-Tree搜索方法与布尔逻辑算法Boolean对冲突集的问题规模极其敏感，在问题规模达到50以后都出现了由于内存溢出而终止算法执行的情况，说明这两种算法不仅实现过程繁琐，而且难以用于解决实际问题；

（2）遗传算法GA在问题规模较小或适中时，搜索效率与离散二进制粒子群BPSO算法相差不大，但当问题规模达到60后，相应的搜索时间开始急剧增加，即不再适用于此种情况的最小碰集求解；

（3）两种BPSO算法（传统BPSO与本论文提出的改进BPSO）对冲突集问题规模不敏感，适用于求解问题规模较大的情况，且规模越大，BPSO算法相对于其它搜索算法的搜索效率越高；

（4）本论文采用的单个粒子寻优与粒子群寻优相结合的改进BPSO算法用于最小碰集搜索时所用的时间比传统BPSO算法用于同样案例所用的时间缩短了近1/3。

综上所述，本文提出的单个粒子寻优与粒子群寻优相结合的BPSO算法具有较高的计算效率和较快的收敛速度，这一实验结果恰恰符合了本文采用该方法搜索最小碰集的出发点，同时该算法还有效地避免了树形搜索算法因剪枝丢失真实解的问题、以及布尔逻辑算法的操作繁琐问题，这也证明了该方法具有较强的实用价值。

4 诊断案例

以某典型卫星电源系统的核心模块PCU（电源控制器）为诊断案例，对其进行定性描述与逻辑推理，重点验证本文提出的最小碰集搜索算法与流程的正确性与实用性。PCU的控制电路原理图见图5,由充电控制电路、放电调节电路、分流调节电路、误差放大电路构成。太阳电池阵输出的能量经过一个二极管直接传递至负载设备；功率管Q2与Q3，分别为分流开关盒控制蓄电池充电的充电开关；Q2与Q3的控制端信号是G1与G2的输出值，G1与G2是误差放大器，分别受母线电压和充电电流控制；Q4和Q5用于避免功率管Q2与Q3发生相互干涉现象。

4.1 诊断案例推理过程

4.1.1 抽象建模

在PCU转化为抽象模型结构图的过程中，进行了适当简化，即不考虑电路中二极管的影响，仅分析功率管和误差放大器。

首先对PCU中的功率管与误差放大器这两类元器件进行抽象建模，以功率管Q2与误差放大器G2为例，所建模型见表3。

建立PCU的抽象模型，按MBD中的规则描述成三元组的形式如下：

①组成元器件集合COMP：COMP=｛G1，G2，Q2，Q3，Q4，Q5，Q6｝。其中，G1与G2为误差放大器，记作VMEA；Q2、Q3、Q4、Q5与Q6为功率管，记作PT。

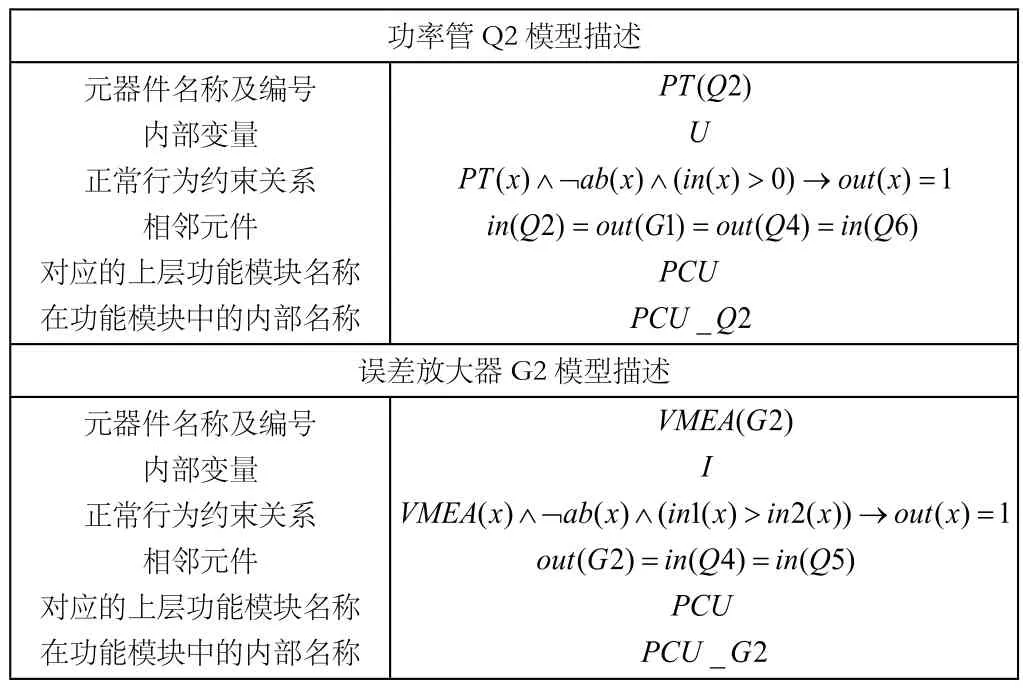
表3 功率管Q2/误差放大器G2模型

②系统描述SD：

组成元器件属性

组成元器件连接关系

元器件功能逻辑描述

观测集OBS：该系统输入端为in（G1）与in（G2），输出端为out（Q2）与out（Q3），构成观测集合OBS=｛ in（G1）, in（G2）, out（Q2）, out（Q3）｝。

4.1.2 冲突识别

假设卫星电源系统实际观测到的现象为PCU模块出现负载母线电压过低，而蓄电池电流正常，即Q2输出异常，Q3输出正常。以此为输入条件，转换为观测集具体取值后，进行冲突识别得到的最小冲突集集合簇为PCM2=｛G1,G2,Q4,Q2｝与PCM3=｛Q2,Q3,Q4,Q5,Q6｝，两者将作为后续搜索最小碰集的输入。

4.1.3 诊断生成

利用本文提出的改进BPSO搜索最小碰集。首先，将最小冲突集集合簇映射到由0、1组成的二值空间中，表示形式如下：

初始设定种群规模P=20，惯性权重ω=0.4、学习因子c1=c2=2、最大迭代次数为Tmax=50，初始化粒子群为一个20×7维的随机二值矩阵x（1），同时初始化一个7维空矩阵Hs用于存储后续搜索的碰集粒子。此处的学习因子和惯性权重作为预置参数，按照大部分BPSO算法的设置方式分别设置为2和0.4。同时，本文分析种群规模P对卫星电源系统这一案例在应用改进BPSO算法搜索最小碰集时产生的影响，获得的分析结果如下表4所示。可以看出，针对这一案例，选择P=20在取得较好的搜索结果的同时耗时最短。

根据本文提出的改进BPSO算法实施流程，借助计算机程序完成

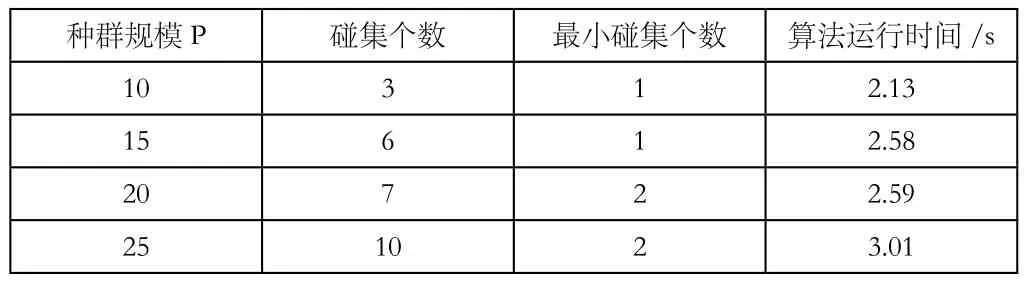
表4 卫星电源系统中不同种群规模下算法性能比较

50次迭代，用于存储碰集粒子的矩阵Hs的变化过程如下：

最终从迭代获得的碰集粒子矩阵Hs中删去所有超集粒子后得到的结果为Hs’ ，具体形式如下：

根据Hs’可以看出，共有2个最小碰集粒子，相应的最小碰集分别为｛Q2｝和｛Q4｝，即“功率管Q2或功率管Q4故障”为改进BPSO算法搜索后输出的诊断结论。

综上，在实际观测到卫星电源系统中电源控制器的负载母线电压过低而蓄电池电流正常的情况下，利用本论文提出的电子产品基于模型诊断方法流程进行故障诊断推理得出的结论是电源控制器故障，具体来说就是电源控制器下的功率管Q2或功率管Q4故障。

4.2 应用效果分析

（1）故障识别准确性。一方面，卫星电源系统的实际观测值所代表的真实情况为“功率管Q2故障”，最终诊断结论中故障元器件也包含Q2，与实际情况相符，验证了本论文提出的诊断方法的正确性；另一方面，通过本论文提出改进BPSO方法流程得到的最终诊断结论中还包含一些非故障部件，如“功率管Q4”，这一结果虽与实际情况不符，但考虑到安全性是本应用案例卫星电源系统的一个重要影响因素，所以在故障诊断推理过程中以略保守的方式进行，得到的结果仍是可以接受的。

（2）故障诊断速度。参考本论文3.4节对5种不同的搜索算法的性能比较分析结果，从中不难看出，利用本文提出的粒子群整体寻优与单个粒子寻优相结合的改进BPSO算法求解最小碰集搜索问题在诊断速度上同样具有较大优势，并且对问题规模不敏感，适用于求解大规模搜索问题。

5 结论

本论文通过将改进BPSO算法引入最小碰集求解，将传统的集合搜索问题转化为二值空间中的矩阵求解问题，并结合粒子群整体寻优与单个粒子寻优，提高算法收敛速度与搜索效率，制定出具体实施流程，并结合实例验证了该算法具有良好的适用性以及较高的工程应用价值。后续，可以继续深入研究动态系统的MBD方法，拓展应用范围。

参考文献：

［1］韩旭,史忠植,林芬等.基于模型诊断的研究进展［J］.高技术通讯,2009,19（05）：543-550.

［2］Reiter R. A theory of diagnosis from first principles［J］. Artificial Intelligence,1987（32）：57-96.

［3］姜云飞,林笠.用布尔代数方法计算最小碰集［J］.计算机学报,2003,26（08）：920-924.

［4］何士玉.基于模型诊断的搜索算法研究及其在配电网中的应用［D］.西南交通大学,2013.

［5］欧阳丹彤,张立明,赵剑等.利用标志传播求解基于模型的故障诊断［J］.仪器仪表学报,2011,32（12）：2857-2862.

DOI：10.16640/j.cnki.37-1222/t.2016.12.215

作者简介：陈忱（1988-），女，重庆人，工程师，主要从事测试性设计与验证、PHM设计技术研究。