基于灰色理论的政府市政工程采购评标研究

宁敬博，舒　欢

(河海大学商学院，江苏南京　211100)



基于灰色理论的政府市政工程采购评标研究

宁敬博，舒欢

(河海大学商学院，江苏南京211100)

摘要：政府工程采购在政府采购中的份额达60%以上，考虑政府工程采购过程中评标的重要性及评价过程本身具有的不确定性和复杂性，提出了构建基于灰色理论的政府工程采购灰靶评标模型。将决策目标下的各个指标值集结为目标综合效果评价值，分别定义正、负靶心，计算各评价对象到正、负靶心的距离，通过空间投影分析计算各方案的综合靶心距，再以综合靶心距最小准则构建目标规划模型，得到各个目标的权重。构建的灰靶评标模型扩展了灰靶决策方法的应用领域，是对政府工程采购评标方法的一次有益尝试。实例分析验证了该模型在政府市政工程采购评标实际应用中的有效性和科学性。

关键词：市政工程；评标；区间灰数；灰靶；综合靶心距

政府工程采购最主要的方式是公开招投标，评标是至关重要的一步，传统的最低价中标原则已经不符合日益追求评标综合效益最大化的要求，因此有必要提出新的评标方法对政府工程采购的投标方案进行优选。国内学者对工程项目是否应该纳入政府采购一直存在着争议，直至《中华人民共和国政府采购法》明确规定工程项目属于政府采购的重要组成部分。国内关于政府工程采购评标方法的研究还处于起步阶段，但对政府采购评标方法的研究值得借鉴。例如：文献[1]提出了综合加权平均差价法；文献[2]和文献[3]基于TOPSIS方法和组合赋权建立了评标模型，对政府工程采购过程中的评标进行了研究；文献[4]探讨了在政府采购评标中使用DEA方法的优势，并用具体实例验证了方法的可行性；文献[5]将粒子滤波算法应用到评标中。已有的研究促进了政府工程采购评标研究的发展，但这些研究中的评价指标值均为实数形式。政府工程采购评标涉及的因素众多，评标过程中具有的不确定性和决策环境的复杂性决定了评价指标值采用区间灰数的形式更能表达决策者的真实意图。

灰靶决策方法是解决多目标决策问题的有效方法之一。其基本思想是在无标准模式条件下，通过测度变换得到灰靶，并在灰靶中寻求靶心作为标准模式，所有决策对象分布在该灰靶上，通过计算，可以得出每一个决策对象和靶心的相对距离，即靶心距，通过比较靶心距的大小而作出决策[6]。灰靶决策方法日益受到重视：文献[7]利用加权马氏距离改进了传统的灰靶决策方法；文献[8]考虑了评价方案与正、负靶心的距离，构建了基于模糊评价法的灰靶决策模型；文献[9]定义了靶心距；文献[10]将理想最优及最劣方案分别定义为正负靶心。灰靶决策方法已经被应用到许多领域：文献[11]构建了基于前景价值函数的灰靶评价模型，并应用于混凝土浇筑方案评价；文献[12]建立了基于灰靶决策与粗糙集的采矿方案优选方法。

灰靶决策方法已被应用于工程领域的评价问题。本研究尝试将灰靶决策方法应用于政府工程采购中招投标阶段的评标、定标环节，基于此构建基于灰色理论的政府工程采购灰靶评标模型。先将各个指标值集结为综合效果评价值，定义正、负靶心，通过空间投影计算各评价方案综合靶心距，以综合靶心距最小准则构建规划模型，求解各目标权重，最后得出可能度矩阵的排序向量，并根据其大小对方案进行排序。

1政府工程采购评标模型

1.1基本假设

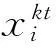
1.2区间灰数的距离及可能度公式

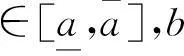
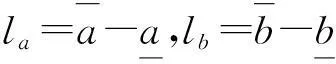
由定义2可知，若将n个区间灰数两两对比，将得到一个n阶矩阵，而此矩阵有模糊互补特征，根据文献[13]：

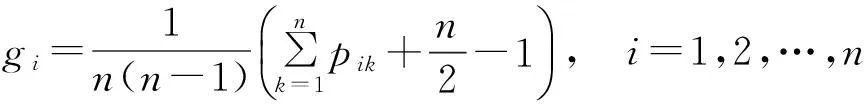
可以得出可能度矩阵向量g=(g1,g2,…,gn)，按照大小就可以对区间灰数作出排序。

2基于灰色理论的政府工程采购评标模型

评价指标量纲的不同会对决策造成干扰，因此先要作无量纲化处理，采用灰色极差变化法。

1) 效益型指标

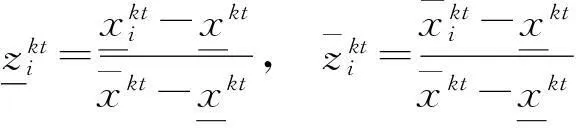
2)成本型指标

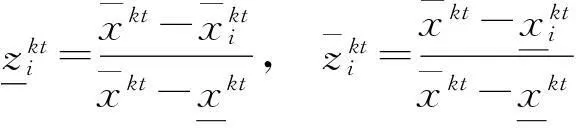
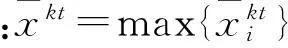
由此得到目标k第t个指标下的一致效果测度矩阵(以下简称矩阵)：

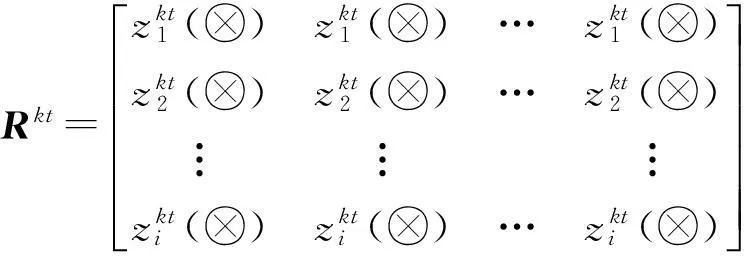
为将第k个目标第t个指标下的矩阵集结为目标k下的综合矩阵，假设在目标k下的各决策指标的权重向量为ω1=(ωk1,ωk2,…,ωkt)，0≤ωkt≤1，则集结方式为

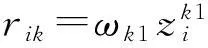
继而得到在目标k下的综合矩阵：

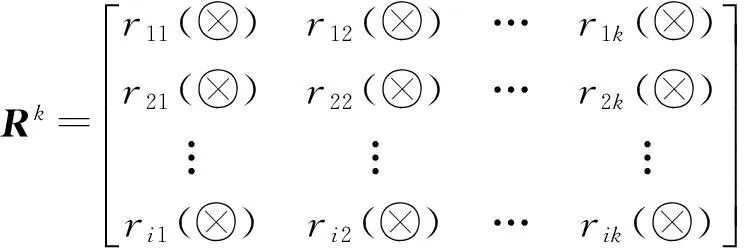
(1)

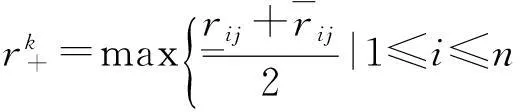
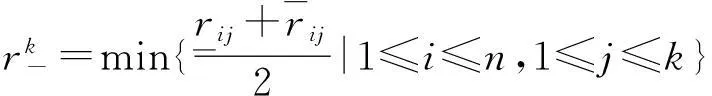
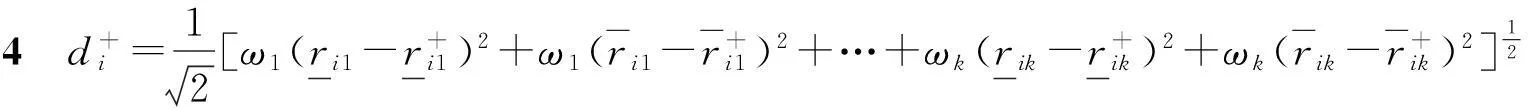
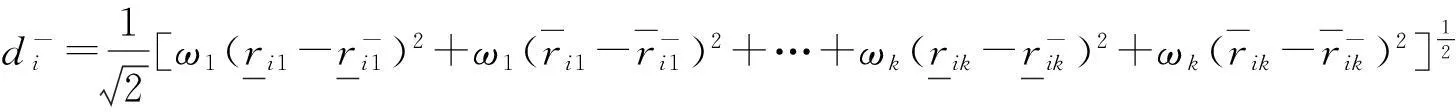
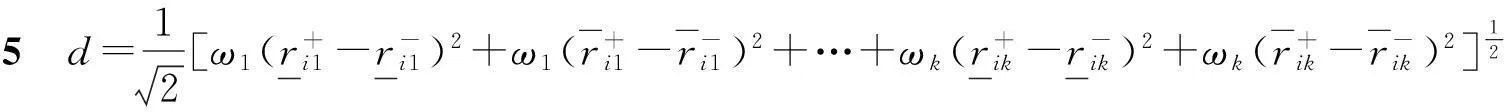
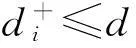
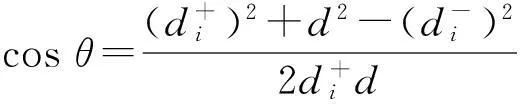
因此，综合靶心距为

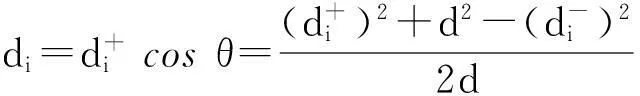
最优目标权重向量的计算可以通过构建优化模型得到。根据文献[14]，目标权重序列ω={ω1,ω2,…,ωk}为灰内涵序列，定义灰熵为

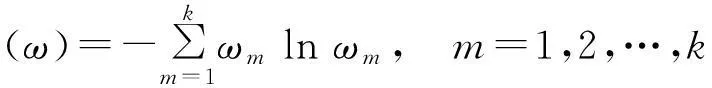
根据极大熵原理，为了使H⊗(ω)极大化及综合靶心距最小，应当调整ωm，使得ω={ω1,ω2,…,ωk}的不确定性尽可能小，由此得到优化模型：

将上述多目标问题单目标化，转化为

一般取λ=0.5。通过运筹学软件对上述模型进行求解，得到目标权重ω={ω1,ω2,…,ωk}。

3实例分析

某市需改建一条市内主干道，该工程项目通过政府采购的形式公开招标，评标综合考虑经济、技术和社会3个方面。最终共4个投标方案进行评标，定性指标中的施工难度、公害大小、安全与否3个指标由专家打分，指标值为实数的视为特殊的区间灰数，具体数据见表1。

运用上文构建的模型，对上述方案进行评标。

无量纲化处理，得到矩阵：

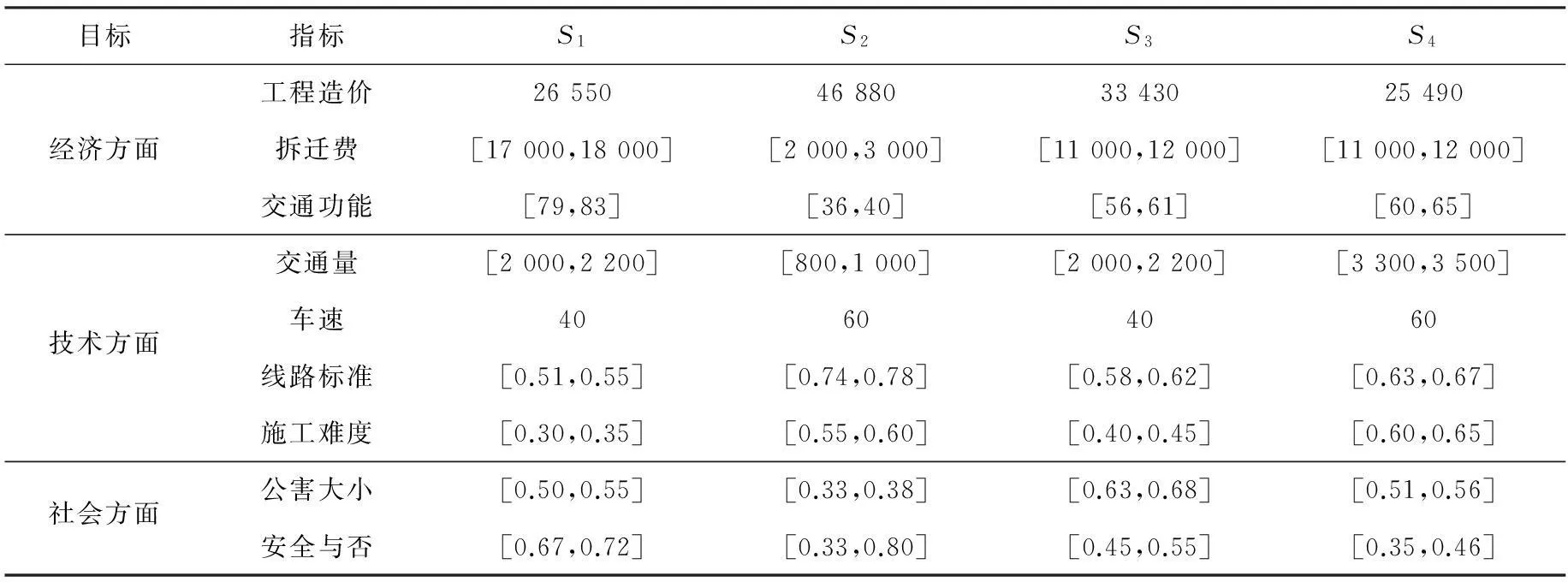
表1　政府工程采购评标的指标体系及效果评价值

计算决策指标的权重[15]：

ω11=0.402,ω12=0.306,ω13=0.292;

ω21=0.357,ω22=0.284,ω23=0.187,ω24=0.172;

ω31=0.456,ω32=0.544。

根据式(1)，得到综合矩阵为

各目标权重为

ω1=0.395,ω2=0.309,ω3=0.296。

根据式(1)，将综合矩阵Rk与目标权重向量ω={ω1,ω2,…,ωk}融合，得到综合测度矩阵为

计算矩阵的排序向量g=(g1,g2,g3,g4)=(0.213,0.125,0.083,0.385)，得到g4>g1>g2>g3，所以方案S4最优。

4结语

研究了政府工程采购中决策信息为区间灰数的评标问题，考虑了在决策环境不确定及复杂条件下目标权重难以确定的问题。通过构建正、负靶心及正、负靶心距离，以综合靶心距最小化构建目标函数以确定目标的权重，再结合区间灰数的可能度对评价对象进行排序以选出最佳方案。本文构建的基于区间灰数的灰靶决策模型扩展了灰靶决策方法的应用领域，是对政府工程采购评标方法的一次有益尝试。必须指出的是，本文并未对政府工程采购评价指标体系的构建展开论述。此外，该模型在政府服务和货物采购评标中是否同样适用，也是今后需要进一步研究的方向。

参考文献/References：

[1] 吴粒,刘松涛,王宏光.政府采购评标方法新探——综合加权平均差价法[J].沈阳工业大学学报,2004,26(5): 579-582.

WU Li,LIU Songtao,WANG Hongguang.Probe into new method of evaluating bids on government procurement：Method of integrated weighted average price difference[J]. Journal of Shenyang University of Technology, 2004, 26(5): 579-582.

[2] 李俏.基于TOPSIS的政府采购招标项目评标方法[J].工业技术经济，2008，27(7)：143-144.

LI Qiao. Method for government procurement bidding project bid evaluation based on TOPSIS[J]. Industrial Technology & Economy, 2008,27(7):143-144.

[3] 舒欢，宁敬博.基于组合赋权与TOPSIS法的政府工程采购评标研究[J].河北工业科技，2015，32(3)：215-218.

SHU Huan,NING Jingbo. Research of government project procurement bid evaluation based on the combination weighting and TOPSIS method[J].Hebei Journal of Industrial Science and Technology, 2015,32(3):215-218.

[4] 胡静.政府采购招标中的DEA评标方法[J].统计与决策, 2007(18):125-127.

HU Jing.The method of DEA bid evaluation in the government procurement bidding [J]. Statistics and Decision, 2007(18):125-127.

[5] 张晓宇,胡士强,梁国壮.粒子滤波算法在评标中的应用[J].河北科技大学学报, 2008,29(4): 341-346.

ZHANG Xiaoyu,HU Shiqiang,LIANG Guozhuang.Evaluating projects by particle filter[J]. Journal of Hebei University of Science and Technology, 2008,29(4): 341-346.

[6] 刘思峰，党耀国.灰色系统理论及其应用[M].北京：科学出版社，2010.

[7] 王正新，党耀国，杨虎.改进的多目标灰靶决策方法[J].系统工程与电子技术，2009，31(10)：2634-2636.WANG Zhengxin,DANG Yaoguo,YANG Hu. Improved multi-objective grey target decision method[J]. Journal of Systems Engineering and Electronics, 2009, 31(10):2634-2636.

[8] 刘婉贞.基于模糊优选法的灰靶决策模型[J].硅谷，2013(18)：41-42.

LIU Wanzhen. The grey target decision model based on fuzzy optimum seeking method [J]. Journal of Silicon Valley, 2013(18): 41-42.

[9] LIU S F, LIN Y. Grey Information: Theory and Practical Applications[M]. London: Springer, 2006.

[10]SONG J, DANG Y G. New decision model of grey target with both the positive clout and the negative clout[J]. Systems Engineering Theory & Practice, 2010, 30(10)：1822-1827.

[11]卞小草，胡志根.基于决策者风险偏好的混凝土浇筑方案灰靶评价模型[J].四川大学学报(工程科学版)，2013，45(4)：21-26.

BIAN Xiaocao,HU Zhigen. Grey target evaluation model of concrete pouring scheme based on risk preference [J]. Journal of Sichuan University (Engineering Science), 2013, 45 (4) : 21-26.

[12]郑海力，陈新.基于灰靶决策理论与粗糙集的采矿方案优选[J].矿业工程研究，2013，28(1)：1-6.

ZHENG Haili,CHEN Xin. Rough set mining plan optimization based on grey target decision theory [J]. Journal of Mining Engineering Research，2013, 28(1):1-6.

[13]徐泽水.模糊互补判断矩阵排序的一种算法[J].系统工程学报，2001，16(4)：311-314.XU Zeshui. Sorting algorithm of a kind of fuzzy complementary judgment matrix[J]. Journal of Systems Engineering, 2001，16(4):311-314.

[14]王正新，党耀国.基于区间数的多目标灰色局势决策模型[J].控制与决策，2009，24(3)：388-392.

WANG Zhengxin,DANG Yaoguo. The multi-objective grey situation decision model based on interval numbers [J]. Control and Decision, 2009, 24(3):388-392.

[15]戴厚平.基于信息熵的区间直觉模糊多属性决策方法[J].重庆文理学院学报(自然科学版)，2009，28(6)：1-4.

DAI Houping. Interval intuitionistic fuzzy multiple attribute decision making based on information entropy method[J]. Journal of Chongqing College of Liberal Arts(Natural Science Edition), 2009, 28(6):1-4.

Research of bidding evaluation in government municipal project procurement based on the grey theory

NING Jingbo， SHU Huan

(Business School, Hohai University， Nanjing， Jiangsu 211100， China)

Abstract:Government project procurement accounts for more than 60% share in government procurement. Considering the importance of the evaluation in government project procurement process and the uncertainty and complexity of evaluation itself, this paper proposes government project procurement gray target evaluation model based on gray theory. First, each index value under the decision goal is combined as effect of the evaluation value for the target assembly; then, the positive and negative bull’s-eyes are defined, the distances of the evaluation objects to the positive and negative bull’s-eyes are calculated, and the integrated clout's distance of each program is obtained； finally, the goal programming model is constructed based on the minimum integrated clout's distance, and each target weight is obtained. The gray target evaluation model expands the application fields of gray target decision-making process, and can be a useful attempt to government procurement project evaluation methods. The case study also verifies that the model is effective and scientific in practical government municipal project procurement.

Keywords:municipal project；bidding evaluation；interval grey number；grey target；integrated clout’s distance

文章编号：1008-1534(2016)03-0183-05

收稿日期：2015-12-16;修回日期：2016-03-23；责任编辑：张士莹

基金项目：国家自然科学基金(51409092)；江苏省自然科学基金(BK20130847)

作者简介：宁敬博(1991—)，男，湖南邵阳人，硕士研究生，主要从事工程项目管理方面的研究。通讯作者：舒欢副教授。E-mail:lenheng@aliyun.com

中图分类号：F224；C934

文献标志码：A

doi:10.7535/hbgykj.2016yx03001

宁敬博，舒欢.基于灰色理论的政府市政工程采购评标研究[J].河北工业科技,2016,33(3):183-187.

NING Jingbo，SHU Huan.Research of bidding evaluation in government municipal project procurement based on the grey theory[J].Hebei Journal of Industrial Science and Technology,2016,33(3):183-187.