数学方法论在数学学习中的运用
2016-06-08曹洁
曹洁


【摘 要】数学方法论是关于数学方法的理论,不仅是对数学本质的认识,也是数学知识的精髓。新课程改革中注重并且加强了数学思想方法的学习,这是培养学生数学素养,形成良好思维品质的关键。而数学方法论同样为学生的数学学习提供了理论指导,有利于学生由传统的机械化的模仿式解题转向能够创新的以实践为基础的解题习惯,以数学思维方法的分析去带动和促进具体数学知识内容的学习与应用。
【关键词】方法论;数学方法论;数学学习
伟大的哲学家、科学家、数学家笛卡尔在《方法导论》一书中总结出四条规则:
(一)不要把任何事物看成是真的,除非对它已经认识清楚了;
(二)利用逐步分析的方法去系统地解决一个问题;
(三)思考时,由简到繁;
(四)要彻底复查(检查)一切之前的各种工作,做到确实无遗漏。
将这四条规律映射在数学学习中,也就是说,首先,要小心避免一些“众所周知”的事情,除非像公理、定理或者之前得到的可靠地结论才可以放进判断的标准之中。其次,把所遇见的每一个难题尽可能的分解成许多个与之关联的细小的,并且可以轻松解决或者是曾经解决过的问题,当然这个“问题”或许已经不是问题。然后,从最简单、最容易认识的对象开始,按照顺序逐步上升到复杂的难以一下子解决的问题,从已知到未知,从简单到复杂,从具体到抽象。最后,检验。把所有想到的情形尽可能的全部罗列出来,确保毫无遗漏。
这四条规则与新课改中所提出的数学学习方法在一定程度上相互吻合:第一,体现出了合情推理与演绎推理的相辅相成的关系,“想象(猜想)的规律要经过验证才能应用”。第二,体现出了整体与局部的关系和转化化归的思想,这要求学生在解题的过程中要注意问题的转化化归,由繁到简、由难到易、由未知到已知,要注意整体代换思想的渗透,要注意一般和特殊的关系等等。第三,体现出了学习应循序渐进的原则。学习应有序而为,循序渐进,不可越节而施。第四,体现出了分类与整合思想、穷举法等数学思想方法。
数学方法论,主要是研究和讨论数学的发展规律(宏观),数学的思想方法以及数学中的发现、发明与创新等法则(微观)的一门学问。数学是一门工具性很强的科学,它具有较高的抽象性、严密性、符号性等特征,为了有效地学习它、应用它、改进它、发展它,就要求对这门科学的发展规律、研究方法、发现与发明等法则都有所掌握。学生在有效的数学方法论的指导下,再加上所学内容的不断加大以及知识建构体系的不断拓展,有益于学生数学思想的建构,将数学学懂,学活在很多人眼里,数学方法不过是深刻挖掘数学教课书中所提到的各种问题,教会老师如何去上好这门课,较高的学术水平才是保证教学质量的关键所在。他们不明白,教育既是一门科学,又是一门技术,只有高深学问,不懂得教育规律是教不好学生的。在课堂中不断向学生输送好的数学方法,远比一味的让学生埋头做题效果要好的多。
让我们来看美籍匈牙利数学教乔治·波利亚在其《数学的发现》中讲到的一道题。
例1:给定三角形的三条边a,b,c,求做一个三角形。
这道题,在现代学生看来,只能算是一到基本的作图题,甚至可能都不会出现在考试卷中。大家都会这样做(图1):
1.做一条线段等于线段a,端点分别为B,C;
2.分别以B,C为圆心,线段b,c的长为半径画圆,两圆相交于点 A或点A′;
3.连接AB,AC和A′B,A′C,则?驻ABC以及?驻A′BC就是所求的三角形。
图1
相信基本所有的学生遇见这道题做到这里就结束了,但是我们回头再看这道题,按照波利亚的《怎样解题》中提到步骤,一步步来分析。
首先,从问题的叙述开始。问题很简单,是要求做一个三角形。第二,考虑怎么做三角形呢?很简单,三条线段顺次首位相连,或者连接不在同一条直线上的三个点。再回到问题中,当我做出了一条线段BC即线段a之后,就等于我已经确定好三角形的两个顶点了,如果在确定一个顶点A,顺次相连就可以了。那么第三步,实施计划。确保计划进行中每一步的准确性,做出一个完美的三角形。第四,回顾。也就是我们现在要做的事。我们把一道求做三角形的题,转化成了已知两点B,C,求第三点A的问题,条件是,点A到点B的距离为c,到点C距离为b,如果只看条件,到点B的距离为c的点和到C点距离为b的点必然会是两条轨迹,我们所要求的点A,就是这两条轨迹的交点。当然了,这样的交点有两个。这样看来,我们就把已知三边求做一个三角形的问题转化成了一道确定两条轨迹交点的问题,这就是一种解题模式——双轨迹模式。
波利亚是这样概括双轨迹模式的:第一,把问题归结为要确定一个点;第二,对于每一部分的条件,未知点都会形成相应的一条轨迹;第三,所有轨迹的交点就是满足所求问题的所有点的集合。这样一来,这就不是一道简单的作图题,我们在它之上找到了一种适合解所有类似问题的解题模式,这才是这道题的意义所在。例如把相对较复杂的求做一角形的内切圆、外接圆,等等一系列问题经过双轨迹解题模式分析之后,就会很轻松容易解决了。以此类推当然还有三轨迹模式以及多轨迹模式。
再来看一道题。
相信提到解方程,很多人一下就会想到经典的鸡兔同笼问题,看看波利亚是怎么看这个问题的。
例2:一个农民有若干只兔子和鸡,这些家畜一共有50个头和140条腿。问这个农民有多少只兔子多少只鸡?
这个问题有很多种解法:
1.尝试法。假设出全部是兔子或者全部是鸡的两种极限模式,列出一个表把所有的可能性罗列出来,结合实际情况,找到答案(表1)。
2.巧解法。将兔子和鸡的腿数减半,这样一共有70条腿,其中,鸡的头数和腿数相等,而兔子的腿数是头数的两倍,从而70-50=20,既为兔子的个数,当然鸡为30只。或者把鸡的翅膀也当做“腿”,同样可以推算出兔子和鸡的个数。
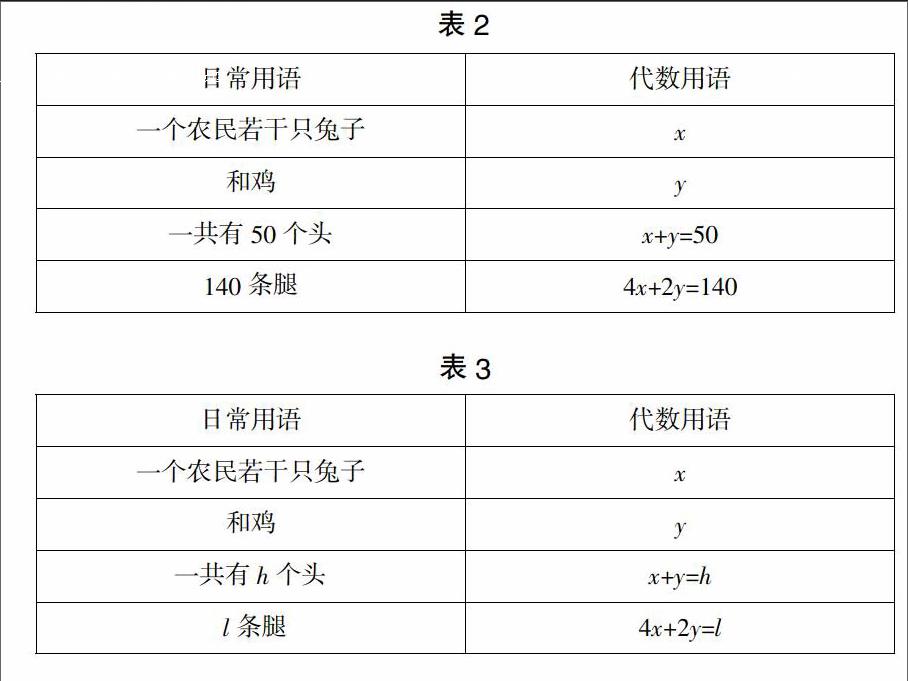
3.代数法。按照笛卡尔“任何问题都能划归为代数问题”的“万能原理”,我们来翻译这道题(表2)。
显然,我们成功的把题目翻译成了两个未知数和两个方程,接下来的工作就是联立方程解方程组。得到方程组的解,x=20y=30这道题也就成功的解答了。那对于这道题,我们要对其“回顾”什么呢?尝试着把给定的数字换成字母,我们再来解这道题。已知这些家畜一共有h个头,l条腿(表3)。
继续联立解方程组得。不难看出,对于新的方程组所得到的两个解,恰巧可以翻译成巧解法中的两种情况。
对于第一种解法,我们称其为“试凑法”,也可以称为“逐次试验法”,我们有理由相信,在一次次的错误尝试之后,最终肯定会得到一个满意的结果。但是相对于较大的数值而言,这个方法显然是不可取的,不仅浪费时间精力,也有可能在不经意的粗心计算下,错过正确的解答。相比较第一种解法,第二种解法要取巧得多,正所谓“巧解法”,然而这个解法与实际的联系并不十分紧密。也正是所谓“巧”,很多学生在做题时不会考虑到这些,即便考虑到了,在数学表述方面也会犹豫不决,再或者说,这个“巧”仅仅只适合于这道题目。对于第三种代数法,既为笛卡尔的解题模式,要求鸡兔各多少只,那就先就把它们假设出来当做已知,设兔子x只,鸡y只,紧接着,根据题目中仅有的两个条件,有50个头140条腿,列出代数式,即x+y=50,4x+2y=140,发现可以联立二元一次方程组,接下来,就是解方程组的问题了。
对于笛卡尔模式,波利亚是这样总结的:首先,在了解问题的基础上,把问题归结为确定若干个未知量;其次,根据已知条件,在未知量和已知量之间建立数学关系,既为方程;最后,联立解方程组。同样的,在笛卡尔解题模式下,我们可以更容易的解答有更多未知数的题目,他们归根到底,就是解方程组的问题。
当然,波利亚提出的数学模式还有很多,所列出的方法也有很多。大多数学生认为,数学,就是计算就是不断的做题,除此之外没有什么意思。通过对以上的两道题的分析,我们发现,其实每一道数学题,都有它自己的存在意义,每一道数学题的背后,都有很深的理论等待我们的发现。如果每个学生在完成题目之后都可以稍加回顾,相信对他来说会是一个不小的进步。同时,通过对以上两道题的仔细分析,我们看到数学方法论在数学学习中的重要意义:
第一,提高理解能力和阅读能力。数学的思想和方法对理解和阅读问题是十分重要的。例如我们要理解和认识接触到的信息比如文字、图形、声音等方式包含的内容时,常常会用到我们的数学思想和方法。通过抽象与概括、分析与归纳、还有比较与分析等方法来加深理解。这些数学的思想和方法对于我们提高理解能力和阅读能力有着十分重要的作用。
第二,培养良好的逻辑思维。虽然数学方法论并不是主要讨论逻辑科学和思维科学,但是数学方法论实质上就是思维活动的方法。数学方法论主要讨论数学逻辑的特点、结构、方法与规律在数学中的应用,从而推广到我们日常的学习和生活当中的应用,对于培养自己良好的逻辑思维有重要的作用。
第三,思考方式的转变。我们在中学学习具体解决数学题目的方法,主要在培养数学基础,而在高等数学中就要认识解决问题的思想和方法。通过学习数学方法论,把以前学过的一些数学思想和方法,例如函数的思想、微分和积分的思想、无限和逼近的思想、抽象与概括、归纳与演绎、归类与分类、比较与类比、分析与综合、联想和直觉等进行了概括和总结。思考方式有了重大的转变,解决问题要想到的不仅仅是眼前看到的一些特点,更加重要的是利用什么样的数学的思想和方法使问题简单化来达到解决问题。
第四,有用的工具。数学的思想和方法并不仅仅是单纯进行理论讨论的内容,现实生活中,数学的思想和方法对于解决实际问题有重要的作用,是解决问题的有力工具。比如在日常经济和管理的决策实践当中面对一些问题时候,如果没有学习过数学的思想和方法是很难找到解决的方法的。通过学习数学方法论。我们便可以想到比如函数、方程、数形结合、微分和积分的思想方法来解决问题。同时,数学的思想和方法对于日常生活的规划也是产生了重要的帮助。
第五,数学的思想和方法是一个永远值得去研究的学科。数学的思想和方法影响是巨大的,小到我们日常的家庭生活和学习,大到一个国家宏观的经济和管理以及成千上万的公司企业的正常运转都离不开数学的思想和方法。特别是现代经济和管理的复杂性越来越要求更高的数学知识技能和解决实际问题的思想和方法。因此数学的思想和方法是很值得深入研究的。
【参考文献】
[1][法]笛卡尔.谈谈方法[M].王太庆,译.商务印书出版社,2009.
[2]郑毓信.数学方法论[M].广西:教育出版社,1996.
[3]GoPolya.How to Solve It [M].阎育苏,译.北京:科学出版社,1982.
[4]GoPolya.Mathematical Discovery.Vol.1[M].刘景麟,等,译.内蒙古人民出版社,1981.
[5]中华人民共和国教育部.义务教育数学课程标准[M].北京:师范大学出版社,2011.
[6]中华人民共和国教育部.普通高中数学课程标准(实验)[M].北京:人民教育出版社,2003.
[责任编辑:杨玉洁]