旋转超声加工非接触供电模型研究

张俊伟，张永俊，梁远标，张　娇，姚　震

（广东工业大学机电工程学院，广东广州510006）



旋转超声加工非接触供电模型研究

张俊伟，张永俊，梁远标，张娇，姚震

（广东工业大学机电工程学院，广东广州510006）

摘要：针对旋转超声加工非接触供电的互感模型和T型模型，结合换能器进行了理论分析和实验研究，并参考非接触供电在其他方面的应用，提出了一种新的适合旋转超声加工的非接触供电模型及其匹配方式，无需考虑耦合系数及原副边线圈间隙过大的问题，具有供电模型简洁、匹配方式简单的优点。根据对比研究的结果搭建了专门的硬件电路，超声压缩实验结果证明了所述模型的可行性和可靠性。

关键词：旋转超声；非接触式供电；理论模型；匹配

传统旋转超声加工的超声振子一般采用碳刷与导电滑环的摩擦接触方式供电，缺点是碳刷磨损快、发热量大、导线裸露、电能传输不稳定、易积炭打火，因此限制了刀具转速，且不易实现自动换刀。提高主轴转速是提高超声加工精度和效率的一条有效途径，所以换能器的非接触供电成为了必然选择。超声换能器可等效为一个电学模型，在旋转超声加工过程中，其电参数受温度、负载等因素的影响不是特别稳定，且采用非接触式供电后，由于其结构的特殊性，一直没有一个较简单、方便又可靠的匹配方式使超声振子处于谐振状态。针对上述问题，本文通过对电动汽车充电、手机充电和旋转超声供电这一类非接触供电的研究现状进行分析，对适合应用在旋转超声加工领域的2种主流非接触供电模型进行理论和实验对比分析，并在此基础上提出了适用于旋转超声振子的简单匹配方式及电参数等效模型和数学模型。

1　超声换能器的等效模型

超声换能器在其谐振频率附近可等效成如图1a所示的电学模型［1］，其中，L1、C1、R1分别为换能器的动态电感、动态电容、动态电阻，三者串联组成动态支路；动态电感L1由换能器的振动质量引起，动态电容C1反映了换能器的刚度，动态电阻R1体现了换能器的阻尼；C0为换能器的静态电容，并联在机械谐振电路上，主要由换能器的尺寸、压电材料和换能器的电极排列决定；R0为换能器的介电损耗。L1、C1、R1是机械和损耗折算过来的电学参量，是机械谐振电路；R0、C0是真实的电学量，但通常R0会达到几兆至几十兆欧姆，在等效电路的分析过程中常忽略不计。

由于静态电容C0的存在，当机械谐振电路处于谐振状态时，换能器处于一种容性状态（图1b），所以超声振子在实际加工过程中不进行匹配；且由于C0的存在，无功功率大，换能器很难振动起来，所以对换能器的静态电容进行补偿是必要的。

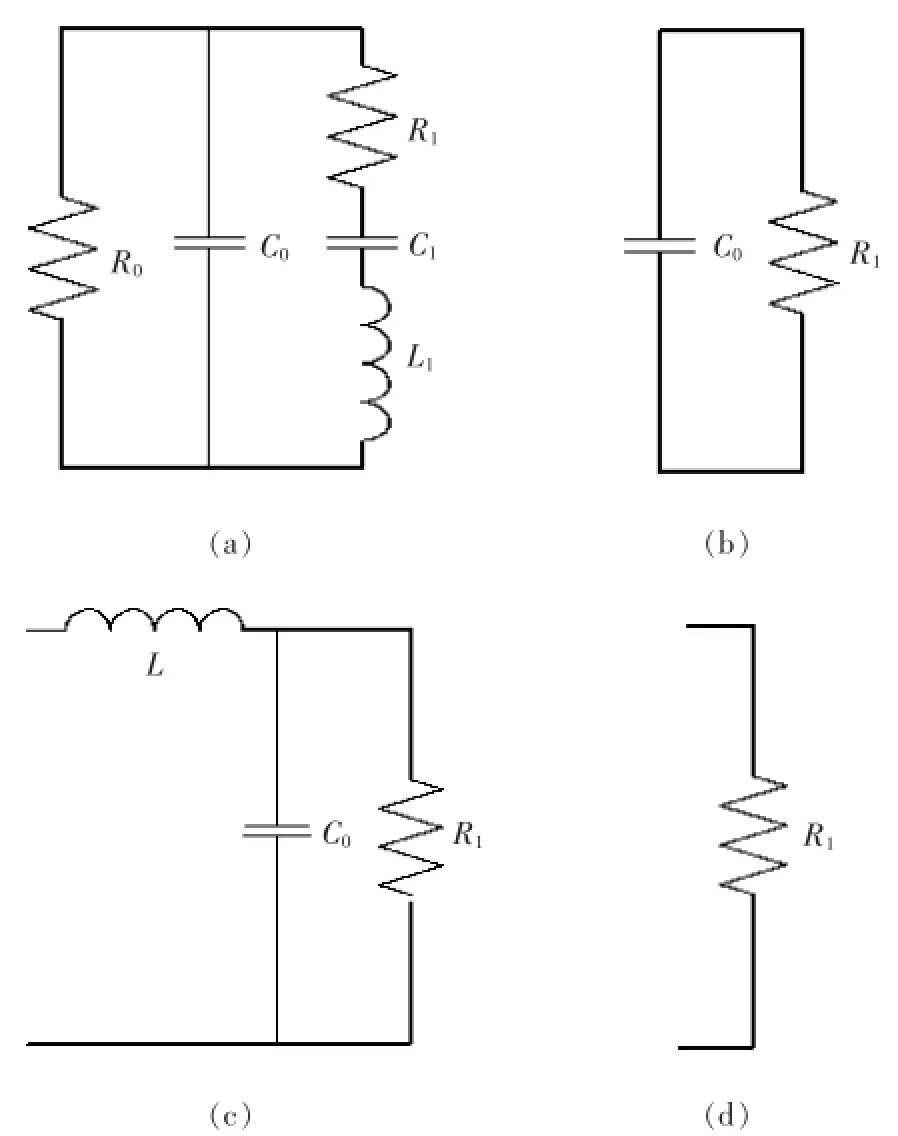
图1　换能器的等效及其匹配电路

匹配电路既能保证电信号高效地传输给换能器，还能起到调谐、整形滤波的作用。一般，超声换能器最简单的匹配方式是串联电感（图1c），其匹配电感后在谐振状态下的阻抗为：

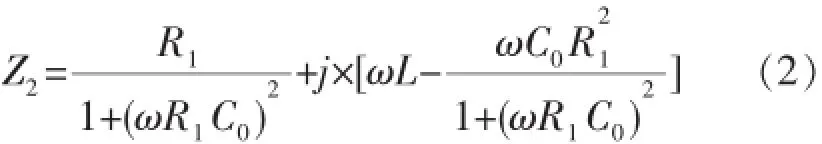
2　非接触式供电

非接触供电的理论基础是电磁感应耦合理论。两股分离同轴的线圈，当其中一股线圈通过变化的交流电时，就会产生变化的磁通，根据电磁感应定律，变化的磁通会引起另一股线圈产生感应电动势。非接触式电能传输的优点在于适用于高速旋转情况下电能的传输，且理论上能量传输的效率不受转速的影响，能克服接触式的诸多缺点。

非接触电磁感应供电装置可分为轴向感应（图2a）和径向感应（图2b）两种方式，其结构可视作变压器，只是磁芯一分为二，相距一个小间隙，本文称之为分离式变压器。轴向感应的原、副边都由磁芯和线圈组成，且副边磁芯安装在主轴上；径向感应组合较自由，原、副边上的两个线圈，既可加磁芯，也可不加磁芯。由于非接触式供电装置（分离式变压器）的副边线圈安装在高速主轴上，其可安装的位置非常有限，且不能影响高速主轴的回转精度；比较轴向和径向两种安装方式发现，轴向感应方式需较大的安装空间，且必须有磁芯，这会使主轴转动惯量大，不易保证动平衡；若采用径向感应方式，主轴上的副边可不加磁芯，这样会大大节省主轴空间，且能明显降低对主轴旋转精度的影响。因此，本文后述的两种模型分析均针对径向供电方式。

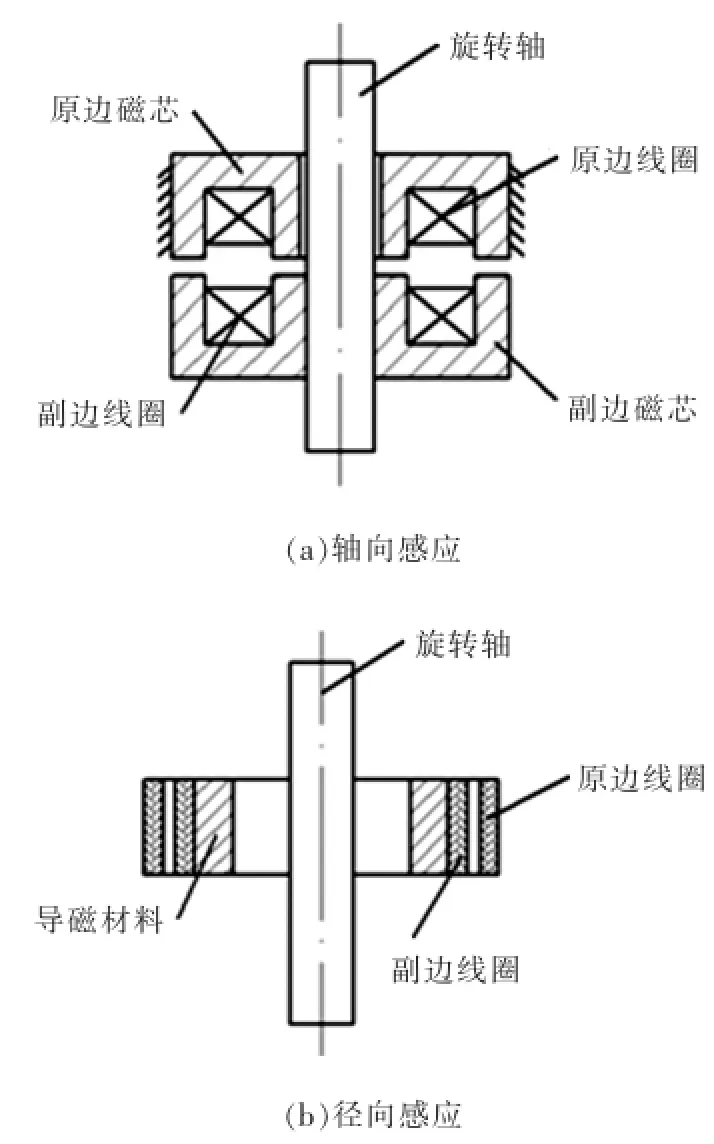
图2　非接触电磁感应供电方式

2.1非接触式供电互感模型

根据国内有关非接触供电应用于旋转超声加工的研究文献来看，采用互感模型结合换能器进行分析是使用最多的模型，该模型主要考虑的是耦合系数、互感系数及原、副边自感等与传递效率的关系，且对非接触供电装置的原、副边都进行匹配电感电容的数学模型分析［2-5］。互感等效模型使用感应电压和反映电压的概念来描述一次、二次线圈之间的耦合效应，优点是不需将漏感和互感分开考虑。

图3是非接触供电装置的电路等效模型，M为原、副边线圈之间的互感，为原边线圈的电压和电流相量，为副边线圈的输出电压和电流相量，Lp、Rp为原边线圈的电感和电阻，Ls、Rs为副边线圈的电感和电阻。根据电磁感应理论，可得互感电路的各回路基本数学方程：

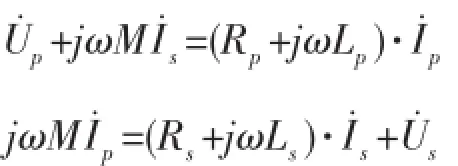
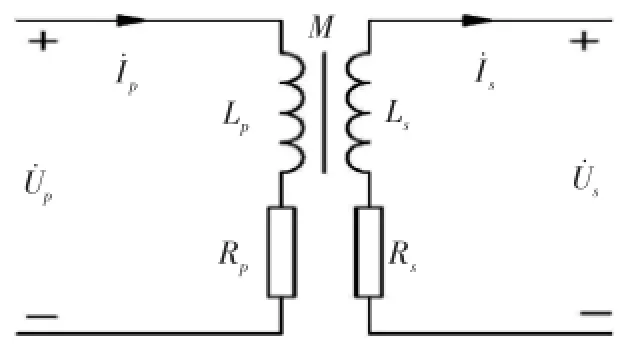
图3　非接触供电装置的互感等效模型

结合超声换能器的电路等效模型，并假设电路处于机械谐振状态，由于非接触供电装置线圈的内阻很小，可忽略不计，所得的等效电路模型见图4。

图4　结合换能器谐振时的互感模型

此时，回路的基本数学方程为：

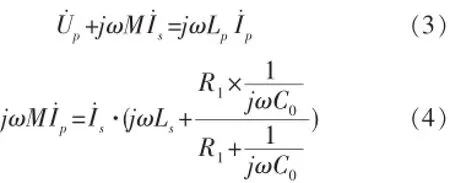
式中：M为两线圈之间的互感。

对式（4）进行化简，可得：

在实际超声加工过程中，计算发现（ωC0R1）2的值远远小于1。例如：图5是一个27 kHz左右的超声振子阻抗图，可知：fs=26.6 kHz、C0=1.25 nF、R1= 160 Ω，则（ωC0R1）2=0.0011，因此，在化简时可忽略不计；且当副边的自感Ls在机械谐振状态下满足Ls，则副边线圈的自感能对超声振子的静态电容进行匹配，此时，式（4）就化简为：

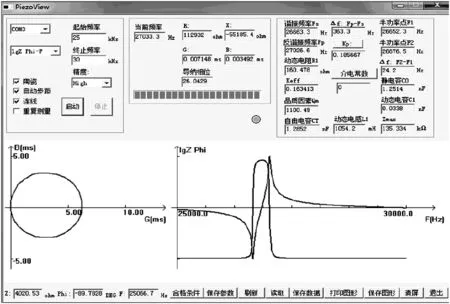
图5　27 kHz超声振子阻抗图

设副边在原边的反映阻抗为Ze，则得到如图6所示的原边等效电路，其中，。可看出，在副边通过匹配使其成为纯电阻状态，反映在原边也是纯电阻，因此要使原边无功功率最小，需通过电容来匹配原边的自感，使原边处于纯电阻状态。此时，原边功率为：

将分子、分母同时乘以原、副边自感，得到：

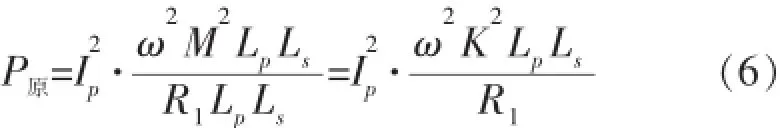
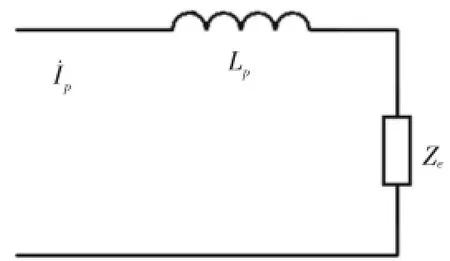
图6　副边在原边的反映阻抗等效电路

由上述推导可知，若要提高功率，就需提高原边电流、频率、耦合系数及减小换能器的动态电阻。频率由超声换能器的机械谐振频率决定；提高电流的方法是提高原边电压；对于耦合系数，在原、副边没有漏磁通的理想情况下，K=1，而常规变压器的耦合系数为K=0.95，耦合系数值较低。

非接触旋转变压器由于原、副边之间存在间隙而会产生很大的漏感，从而使原、副边的耦合系数降低，进而影响原、副边的传递效率。分析可知，上述模型采用了非接触供电装置的原、副边线圈自感进行匹配，且等价于式（2）的串联匹配。然而，由于非接触供电装置实际上是一种分离式变压器，在变压器内很难分清互感和自感，且变压器工作主要也是以互感为主。此外，要使自感完全串联匹配换能器的电容很难，尤其是极易受到换能器静态电容的影响，使振子几乎不能振。

2.2非接触式供电T型模型

根据非接触式供电装置的变压器互感模型，气隙直接影响着耦合系数，从而影响传递效率。由于本文讨论的非接触供电装置为径向供电结构，所以当线圈尺寸确定后，原、副边的气隙也即固定，不能像轴向供电装置那样可调。采用T型模型就要充分考虑到非接触式供电装置（分离式变压器）的漏感，因为气隙越大，漏感越大。图7是变压器漏感模型，松耦合变压器简化成由理想变压器、漏感Ls和励磁电感Lm组成，C0为换能器的静态电容，R1为换能器机械谐振电路谐振时的静态电阻。因此，该非接触供电装置的模型就较简单，主要参数仅漏感、励磁电感、原副边匝数比3个。

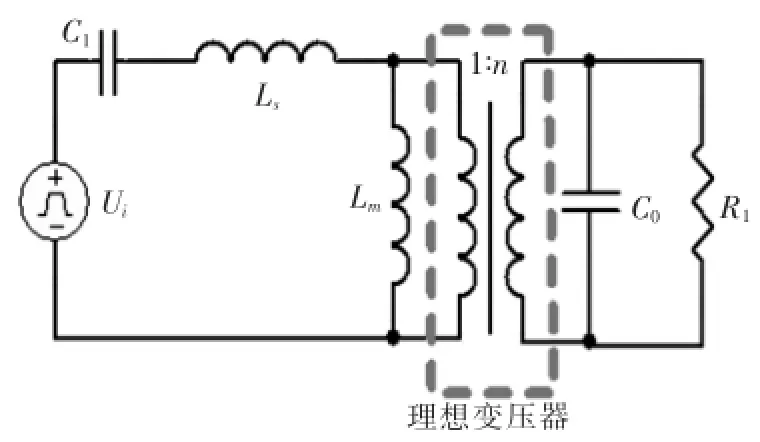
图7　变压器T型模型

非接触供电装置（分离式变压器）的励磁电感和漏感可用LCR电桥仪测量得到，即分别测量变压器副边开路和短路时的原边电感，作为分离式变压器的漏感Ls和励磁电感Lm，并用Lm匹配换能器的静态电容，再串联一个电容来匹配漏感，形成LLCC的匹配方式［6］，这样就有：

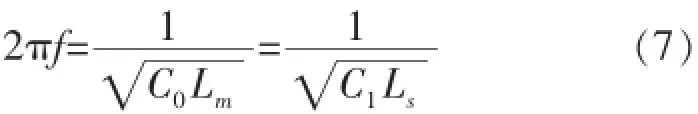
式中：C1为原边匹配电容；f为换能器的谐振频率。这样，非接触式供电装置的变压器模型分析就变得很简单，匹配方式也变得较容易，且当式（7）的2个等式全满足的情况下，无功功率最小，副边获得的能量最大，传递效率能达到最大。

由此可看出，T型模型比互感模型简单很多，没有很复杂的理论推导，也不像互感模型那样，在理论推导过程中将很多细节都理想化，导致与实际情况相差太大，T型模型匹配方式只是在原边串联了一个电容去抵消漏感带来的无功功率。同时，静态电容的影响被激励电感所抵消，即使激励电感不完全，匹配静态电容影响也不大，因为通过前面的漏感和匹配电容的作用已使电压和电流同相，从漏感输出个正弦波，不受换能器参数变化的影响，这样能保证换能器一直处于谐振状态。

3　硬件电路

通过上述分析对比，针对非接触式供电装置采用径向供电的T型模型，对主电路进行如下处理：超声电源适用到超声振子时需进行阻抗匹配，在逆变输出接一个高频变压器，使变压器的输出阻抗等于超声振子的动态电阻，因此，非接触供电装置的原副边匝数比设计成1∶1（图8）。

图8　原副边匝数比为1∶1

由于非接触变压器传递能量时会有损失，为了提高副边的功率，主电路采用全桥逆变（图9）。

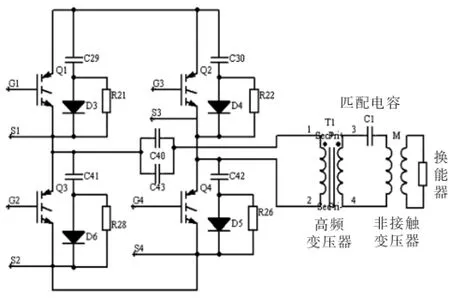
图9　全桥逆变主电路

4　实验

结合上述分析，在非接触供电装置（分离式变压器）的T型模型中，原边采用串联电容进行匹配。为验证该模型的正确性，同时简化实验工作，搭建了一个静态（即非旋转）的非接触供电装置用于生物质燃料的超声压缩实验。由于非接触式供电运用于旋转时，其能量的传递不受转速的影响，因此，虽然实验装置不旋转，但非接触供电实验结果同样适用于旋转超声加工。

实验中，直流可调输出电压为25 V，气缸预压力为0.3 MPa，每个压块锯末的质量为1.5 g，压块的模具直径为20 mm。在相同的压缩时间下，每组实验取3个压块样本，并求压缩高度的平均值。实验对比了常规供电的超声压缩、非接触式供电的超声压缩、无超声压缩3种情况下，锯末成块的高度和密度，结果见图10、图11。可看出，采用非接触供电压缩的锯末块密度和高度与常规超声压缩很接近，且密度明显大于无超声压缩，说明采用非接触供电的T型模型进行匹配能得到较好的加工效果。

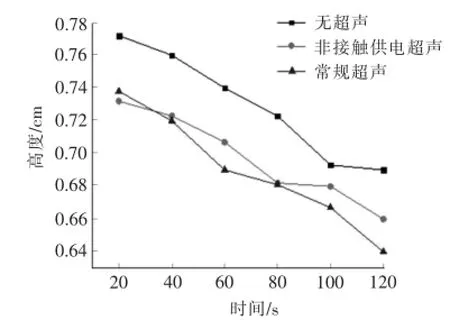
图10　压缩块高度的对比

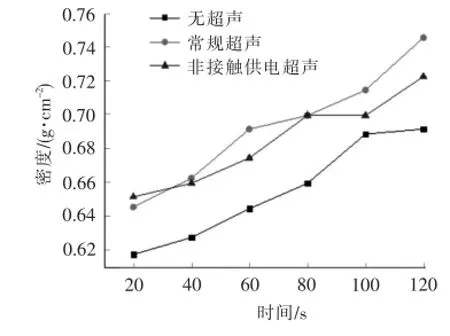
图11　压缩块密度的对比

5　结束语

本文对旋转超声加工非接触式供电的2种常用理论模型进行了对比研究，分析了其各自的优缺点，搭建了相关的硬件电路，并进行了实验验证。互感模型不需考虑漏感和激励电感，模型简单，但推导公式复杂，中间理想化简化过程太多，受各种因素的影响也大，且该模型相当于串联匹配的超声振子，易受振子加工时电参数的变化影响，不易实现振子的谐振，理论实践差太远。而T型模型中，非接触供电装置的匹配电路大为简化，且加工电压和电流受超声振子电参数变化的影响不大，故将非接触供电应用到高速旋转主轴的超声加工中具有参考价值。

参考文献：

［1］KRIMHOLTZ R，LEEDOM D A，MATTHAEI G L. New equivalent circuits for elementary piezoelectric transducers［J］. Electronics Letters，1970，6（13）：398-399.

［2］庞明鑫.非接触式超声电能传递装置的设计理论及实验研究［D］.太原：太原理工大学，2010.

［3］马付建.超声辅助加工系统研发及其在复合材料加工中的应用［D］.大连：大连理工大学，2013.

［4］黄浩.超声辅助加工非接触式电能传输系统仿真分析［D］.大连：大连理工大学，2013.

［5］章智伟.超声内圆磨削系统的关键技术及实验研究［D］.郑州：河南工业大学，2011.

［6］BORTIS D，KOVACEVIC I，FÄSSLER L，et al. Optimization of rotary transformer for high-speed applications［C］// Control and Modeling for Power Electronics，2013 IEEE 14th Workshop on. Salt Lake City，2013：1-6.

Study on Non-contact Power Supply Model in Rotating Ultrasonic Machining

Zhang Junwei，Zhang Yongjun，Liang Yuanbiao，Zhang Jiao，Yao Zhen
（School of Electro-mechanical Engineering，Guangdong University of Technology，Guangzhou 510006，China）

Abstract：Contactless rotary ultrasonic machining for the mutual supply model and T-type model，combined transducer theoretical analysis and experimental research，and with reference to the noncontact power supply applications in other areas，a new suit rotary ultrasonic machining non-contact power supply model and its matching are proposed，irrespective of the coupling coefficient and the original secondary coil gap is too big problem with power supply model is simple and easy matching of advantages. According to results of the comparative study，a dedicated hardware circuit for ultrasound compression is built. The feasibility and reliability of the model is proved by the test.

Key words：rotary ultrasonic；non-contact power supply；theoretical model；matching

中图分类号：TG663

文献标识码：A

文章编号：1009－279X（2016）02－0045-05

收稿日期：2015-09-30

基金项目：国家自然科学基金资助项目（51275097）；机械系统与振动国家重点实验室开放基金资助项目（MSV-2013-08）

第一作者简介：张俊伟，男，1991年生，硕士研究生。