EKF和UKF在非线性组合导航系统中的对比研究

吴春光，李双明，潘玉纯

（92941部队，葫芦岛　125000）



EKF和UKF在非线性组合导航系统中的对比研究

吴春光，李双明，潘玉纯

（92941部队，葫芦岛125000）

摘要：采用组合导航系统在对目标的位置、航向进行测量时，其状态模型和观测模型中存在非线性问题，采用基于EKF 和UKF的非线性滤波算法以改善传统Kalman滤波的估计精度，并保证算法收敛性。通过建立组合导航的状态方程和量测方程，分别采用EKF和UKF对状态方程中的非线性部分进行离散化，仿真实验结果表明，采用基于UKF的非线性导航算法能有效提高导航位置精度和系统稳定性。

关键词：EKF；UKF；组合导航

导航系统在航海领域有着广泛的应用［1，2］，在实时获取航行时的位置、速度、航向等状态信息方面具有重要实际意义。在船舶导航系统中常用惯导和GPS组合导航系统，既能实现依靠惯导提供多种精确的导航参数信息，又确保在海上长航保持导航精度以及避免复杂环境的电子干扰［3，4］。导航系统本质上是非线性系统，通常采用的线性误差状态方程是在假定惯导系统姿态误差为小量的条件下导出，但当惯性器件精度较差或者载体做大机动运动时惯导系统失准角很大，此时导航系统中的非线性因素不可忽略，工程上常用非线性滤波算法进行处理［5］。本文通过仿真计算，对比分析EKF 和UKF两种滤波算法在非线性组合导航系统中的应用。

1　组合导航系统数学模型

组合导航系统的实质是一个多传感器的数据融合系统，使用扩展卡尔曼滤波器的核心是建立导航系统的状态方程和量测方程，滤波器选取各导航参数的误差量作为状态变量［6，7］。本文选取位置误差、速度误差、姿态角误差作为非线性组合导航系统的状态量，并将陀螺随机漂移误差和加速度计零偏误差作为扩充状态量。

1.1系统状态方程

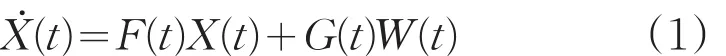
选择东、北、天地理坐标系为导航坐标系，建立系统的状态方程：其中，X（t）=［φE，φN，φU，δVE，δVN，δV，δL，δλ，δh，εE，εN，εU，∇E，∇N，∇U］T为状态向量，φE、φN、φU为姿态误差角，δVE、δVN、δVU为速度误差，δL、δλ、δh为位置误差，εE、εN、εU为陀螺的随机常值漂移，∇E、∇N、∇U为加速度计零偏。

系统过程白噪声矩阵W（t）为：

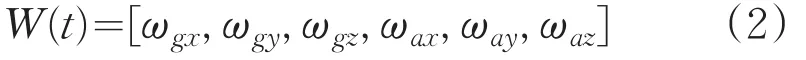
系统状态转移矩阵F（t）为：

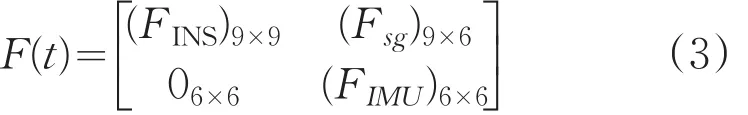
式（3）中FINS由惯导基本误差方程决定，

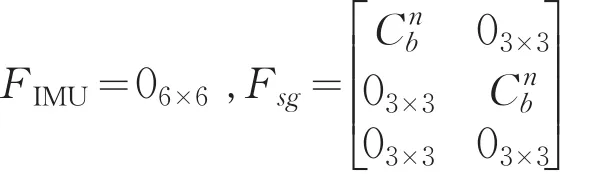
系统噪声传播矩阵G（t）为：

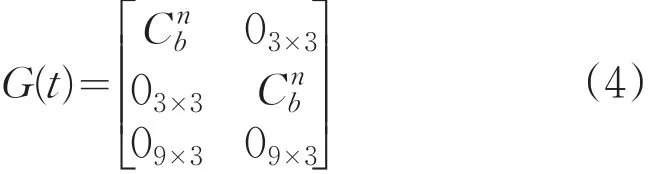
1.2系统量测方程

本文采用位置、速度组合模式，建立位置量测方程和速度量测方程。

1.2.1位置量测方程

导航系统给出的实时位置误差包含纬度、经度和高程。以L、λ和h分别代表载体真实纬度、经度和高程；LI、λI和hI代表惯导输出纬度、经度和高程；LG、λG和hG代表GPS接收机输出纬度、经度和高程；NN、NE和NU为GPS接收机导航系下的位置量测误差，则有：

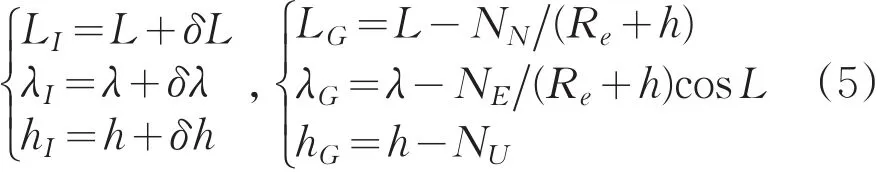
取惯导和GPS输出的位置差值作为系统量测值，则位置量测方程为：

式中，HP（t）=［03×6⋮diag［（Re+h），（Re+h）cos L，1］⋮03×6］，VP（t）=［NN，NE，NU］T。

1.2.2速度量测方程

以VE、VN和VU分别代表载体真实东北天方向速度；VIE、VIN和VIU代表惯导输出的东北天方向速度；VGE、VGN和VGU代表GPS接收机输出的东北天方向速度。则有：

式中，NVE，NVN，NVU为GPS接收机沿东北天方向速度量测误差，取惯导和GPS输出的速度差值作为系统量测值，则速度量测方程为：

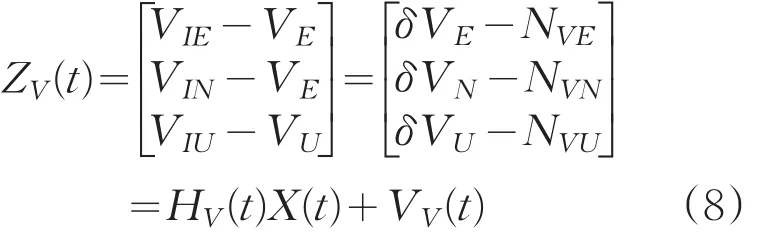
式中，HV（t）=［03×3⋮diag［1，1，1］⋮03×9］，VV（t）=［NVE，NVN，NVU］T。

由式（6）和式（8）建立系统的量测方程为：

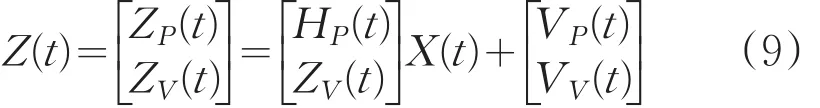
1.3离散卡尔曼滤波

卡尔曼滤波是从一系列不完全且包含噪声的量测值中估计动态系统的状态，首先便于系统的描述计算，采用离散化方程来描述系统，离散后系统方程如下：

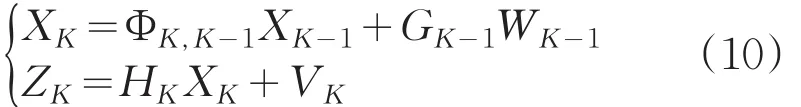
式中，ΦK，K-1为K-1到K时刻的n×n阶系统转移矩阵；GK-1为n×r阶系统噪声矩阵；WK-1为K-1时刻的r维的系统噪声；HK为K时刻的m×n阶系统量测矩阵；VK为K时刻的m维的测量噪声。且要求｛WK｝和｛VK｝为互不相关均值为零，方差分别为QK和RK的白噪声序列。滤波算法中初始状态向量的一、二阶统计特性为E｛X0｝=mX0，Var｛X0｝=CX0，卡尔曼滤波要求mX0和CX0为已知量，且X0和和｛WK｝与｛VK｝都不相关。离散卡尔曼滤波方程组如下：｛WK｝与｛VK｝都不相关。离散卡尔曼滤波方程组如下：

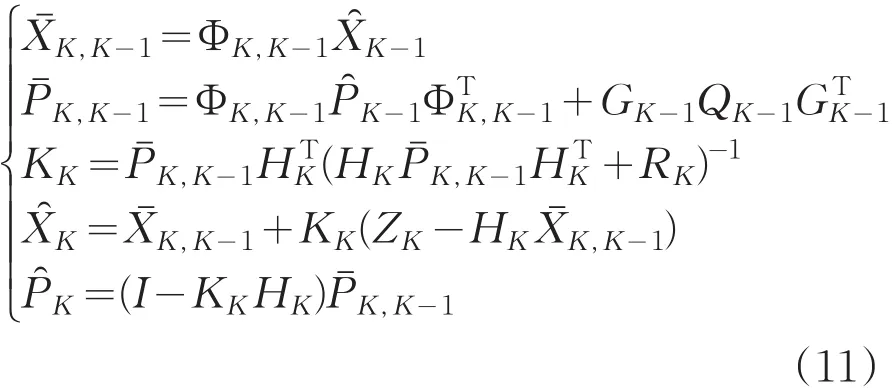
通过式（1）、（9）即可对导航系统方程离散化。

2　非线性滤波算法

传统线性卡尔曼滤波会导致滤波状态发散，而采用非线性卡尔曼滤波算法EKF和UKF会取得较好效果［8，9］。

2.1扩展卡尔曼滤波（EKF）算法

扩展卡尔曼滤波是用泰勒级数展开，生成状态值X和量测值Z的联合分布的高斯近似，从而解决非线性问题。考虑非线性系统模型为：

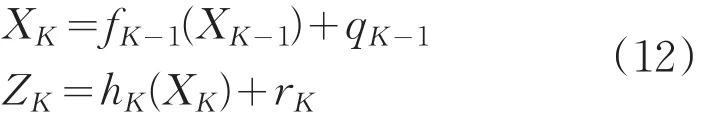
扩展卡尔曼滤波方程组如下：

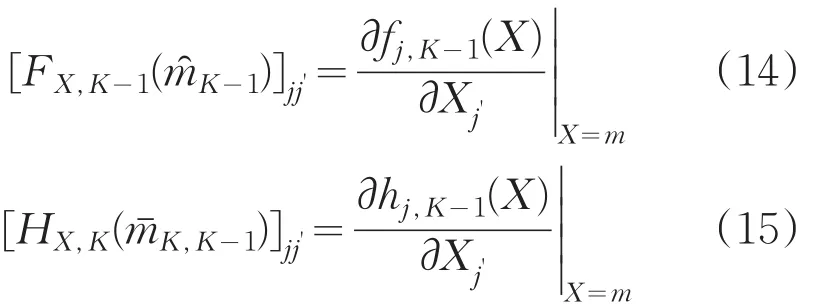
2.2无迹卡尔曼滤波（UKF）算法

类似于扩展卡尔曼滤波使用泰勒级数展开，无迹卡尔曼滤波是用无迹变换（UT，unscented transform）生成状态值X和量测值Z的联合分布的高斯近似来解决非线性问题。对式（12）中UT变换生成联合高斯分布：

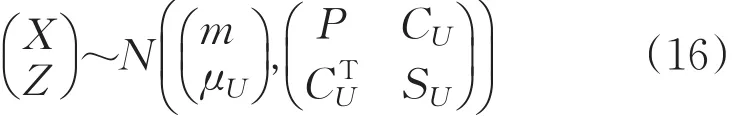
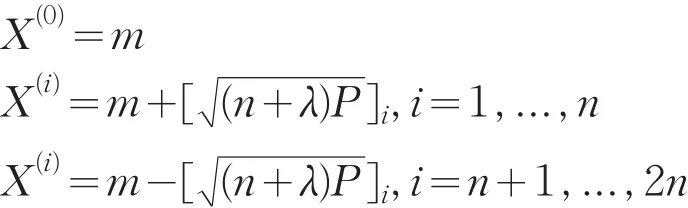
以及相应权值：

ωm

（0）=λ/（n+λ）

ωc（0）=λ/（n+λ）+（1-α2+β）

ωm

（i）=1/［2（n+λ）］，i=1，...，2n

ωc（i）=1/［2（n+λ）］，i=1，...，2n

其中：参数λ=α2（n+κ）-n，α、β、κ均为正数。

（2）每个σ点通过非线性函数h：Z（i）=h（X（i）），i=0，...，2n。从而量测值Z的估计均值和协方差为：

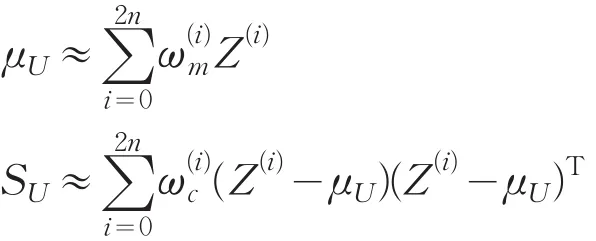
以及X和Z的互协方差为：

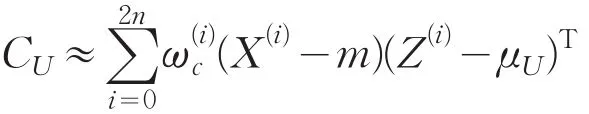
写成矩阵形式为：

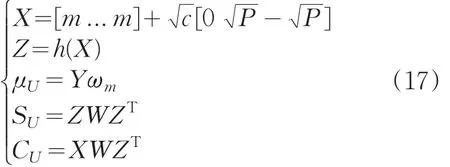
其中：X为σ点矩阵，c=α2（n+κ），矩阵W= （1-［ωm...ωm］）×diag（ω（0）c...ω（2n）

c）×（1-［ωm...ωm］）T向量ωm=［ω（0）m...ω（2n）m］T。

由此，无迹卡尔曼滤波方程组如下：

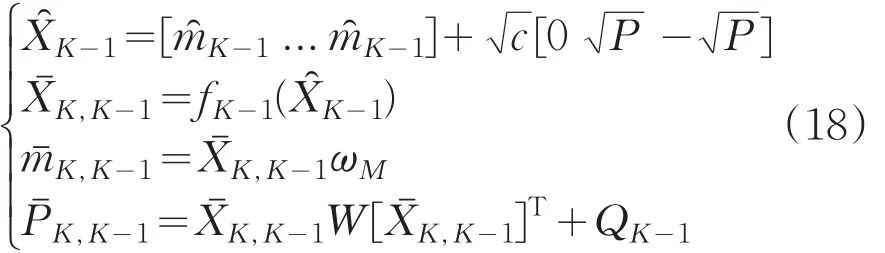
（2）更新过程（计算预测均值μK，量测值协方差矩阵SK）：

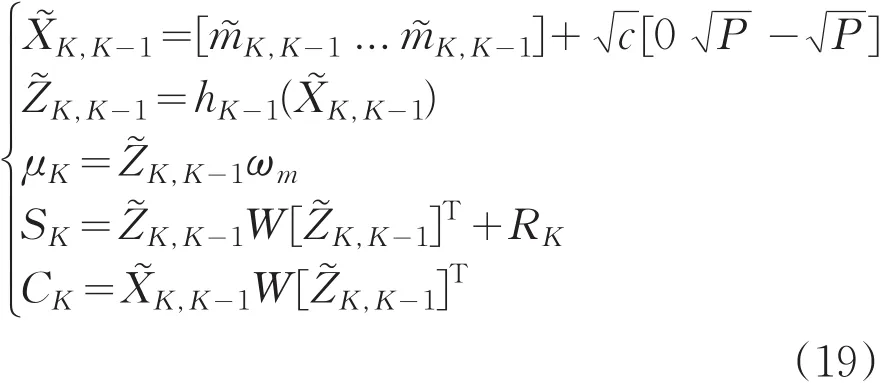
（计算滤波增益和跟新均值和协方差）

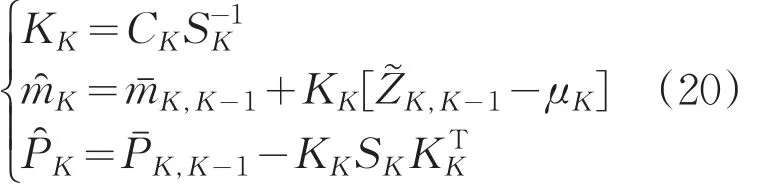
3　仿真实验

根据海上航行数据做仿真实验，分别用标准卡尔曼滤波、扩展卡尔曼滤波和无迹卡尔曼滤波进行滤波和平滑处理。仿真步长t=1s，取200个采样点。目标从原点出发，速度（，）=（1，0）（s/m）；在40s时，目标以转向比ω=1左转；在100s时，目标停止转动，保持1min匀速直线运动；在110s时，目标以转向比ω=-1右转；在140s时，目标停止转动，保持60s匀速直线运动。目标运动轨迹和三种滤波算法结果如图1和图2所示。

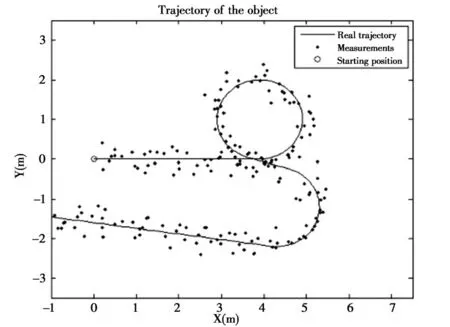
图1　目标真实轨迹和采样量测数据

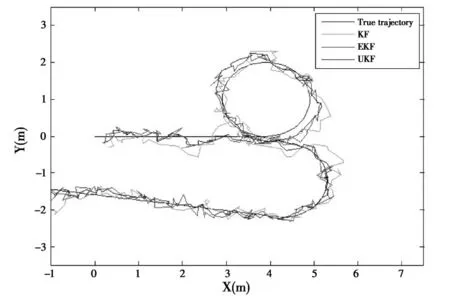
图2　使用三种滤波算法对目标位置估计结果对比

图3给出三种滤波算法对目标位置估计的均方误差MSE对比。在给出的三种滤波方法中，EKF 和UKF的滤波估计在仿真结果中表现基本相同，且都比标准KF效果更好，其中UKF更接近于真实轨迹值，由表1给出的平均MSE估计值也可以明显的反映出来。

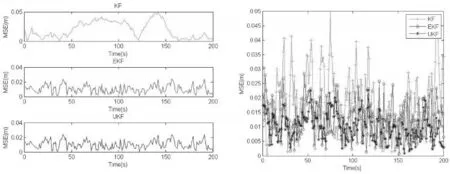
图3　三种滤波算法位置估计MSE（均方误差）结果对比

表1　三种滤波算法位置估计的平均MSE（均方误差）

4　结论

本文介绍的非线性组合导航系统是根据某一具体工程应用而设计，建立了组合导航系统数学模型，对EKF和UKF滤波算法在组合导航系统中的应用进行了对比研究。仿真结果表明，在非线性导航系统中使用UKF滤波算法的导航定位精度和系统稳定性上要优于EKF，对于提高海上导航定位精度、实时获得目标姿态信息具有重要意义。

参考文献

［1］李旻.舰艇导航技术的设备与发展［J］.舰船电子工程，2015，35（5）：14-16.

［2］郭姣，李天伟，黎才鑫，等.舰载导航装备综合效能评估指标体系的研究［J］.现代电子技术，2014，37（17）：140-143.

［3］朱栋山.船用SINS/GPS/CNS组合导航信息融合算法研究［D］.北京：国防科学技术大学，2012.

［4］张晓亮.GPS/SINS组合导航系统应用研究［D］.南京：南京理工大学，2013.

［5］赵琳，王小旭，丁继成，等.组合导航系统非线性滤波算法综述［J］.中国惯性技术学报，2009，17（1）：47-58.

［6］严恭敏.捷联惯导算法及车载组合导航系统研究［D］.西安：西北工业大学，2004.

［7］马涛.光纤捷联惯导及其卫星深组合导航算法研究［D］.哈尔滨：哈尔滨工程大学，2013.

［8］赵思浩，陆明泉，冯振明.EKF与UKF在紧耦合组合导航系统中的应用［J］.系统工程与电子技术，2009（10）：2450-2454.

［9］Nicola Ceccarelli，Fabrizio Scortecci. Comparison of EKF and UKF for spacecraft localization via angle measurements［J］.IEEE transactions on Aerospace and electronic systems，2011，47（1）：75-84.

Comparison of EKF and UKF Applied in Nonlinear Navigation System

WU Chunguang，LI Shuangming，PAN Yuchun
（92941 Troops，Huludao 125000）

Abstract：For realizing the real-timemeasurement of the object on position or heading，and achieving real-time data，the nonlinear integrated navigation system based on EKF and UKF was used instead of the Kalman filter. We discussed the working principle and system composition，then represented system model and analyzed the application of EKF and UKF. The experimental results indicate that using nonlinear integrated navigationsystem based on UKF can effectively improve the navigation accuracy and system stability.

Key words：EKF；UKF；nonlinear integrated navigation system

中图分类号：V249.3

文献标识码：A

文章编号：1672-9870（2016）02-0082-04

收稿日期：2015-09-24

作者简介：吴春光（1975-），男，高级工程师，E-mail：cg2196@126.com