回转主轴垂直度及安装偏心对轮毂跳动检测的影响分析

刘忠夫，王振宏

（长春理工大学　机电工程学院，长春　130022）



回转主轴垂直度及安装偏心对轮毂跳动检测的影响分析

刘忠夫，王振宏

（长春理工大学机电工程学院，长春130022）

摘要：针对轮毂跳动量检测系统结构，分析了影响系统检测精度的误差来源，通过对引起误差结构的建模与分析，根据结构原理，得到回转主轴倾角与轮毂径向、轴向跳动量之间函数关系以及由于轮毂安装偏心引起的径向跳动随旋转角度周期性变化的函数。通过Matlab仿真和控制变量分析，验证理论，为检测系统的精密装配和调试提供了理论依据，对减小系统误差具有实际意义。

关键词：跳动量检测；垂直度；回转偏心；误差分析

随着汽车产业的迅速发展，汽车轮毂生产厂商对轮毂的质量提出了严格的检测要求。汽车轮毂的跳动量检测是其质量检测的重要项目之一，轮毂跳动量检测的精度要求也随着科技的发展不断提高。目前通常采用由主轴带动轮毂旋转，应用接触式测量方法的跳动量检测系统。该系统通过检测探头直接接触轮毂待测表面的方式，对汽车轮毂的径向和轴向跳动量进行测量，以实现对轮毂的质量检验。但是由于测量系统在装配过程中回转主轴存在垂直度误差，轮毂定位时存在回转偏心误差［1］，所以会使检测系统的测量值产生较大偏差。文章针对系统结构及影响测量的因素进行了分析和研究，为检测系统精密装配、调试提供了理论依据，对减小系统误差具有实际意义。

1　检测系统结构模型

轮毂跳动量检测系统主要对轮毂与轮胎接触表面的两侧进行跳动量测量。通过电机带动主轴旋转，使装卡在主轴上端的轮毂同步旋转。检测探头采用倾斜45°的方式紧贴轮毂两处检测点，如图1所示，主轴电机通过带传动的方式，带动旋转主轴平稳低速旋转。主轴顶端承载平台上，通过气动胀紧装置，使轮毂内侧下端面紧贴主轴承载面，保证汽车轮毂以其下端面为基准水平固定，并与主轴无相对转动。检测探头倾斜45°进行检测，微小位移分解为水平和竖直两个方向的分量，这就将轮毂的径向、轴向跳动量转化为检测探头的水平和竖直运动。在跳动检测装置内，利用激光三角测距原理，对检测探头后端的水平和竖直两个方向进行高精度的微位移测距，得出两个方向的跳动量。

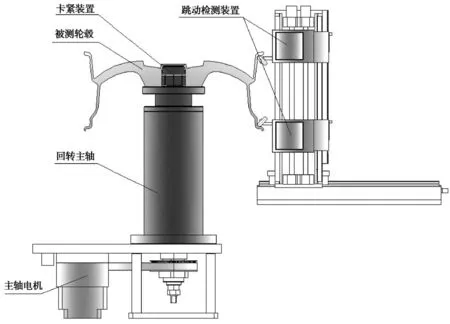
图1　检测系统结构示意图

2　主轴不垂直引起的误差

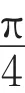
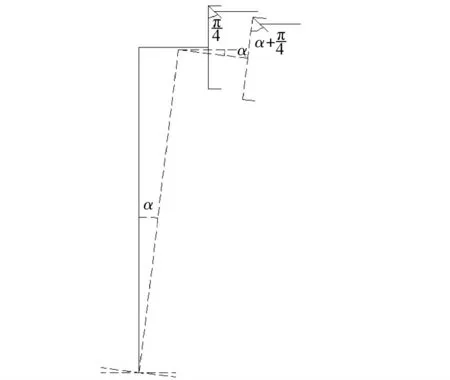
图2　主轴倾斜角度α示意图

为方便研究，根据结构原理，假设主轴垂直方向未发生偏转，而将检测探头沿逆时针方向旋转α角度，此种α转化与主轴偏转情形相同。假设轮毂某点存在跳动量，其径向与轴向分量分别为x、y，如图3所示。

图3　x、y跳动分量示意图

由于存在倾角α，x方向位移分解为相互垂直的两个方向的位移x1、x2，其中

同理，轴向跳动y分解为

这样，反映到检测系统中，实际检测到的径向跳动ξ与轴向跳动ζ为各个方向分量的叠加，即

代入得

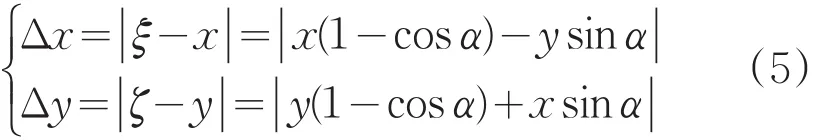
由式（5）可以看出，当倾角α=0，即主轴倾角为零时，Δx、Δy均为零。而随着倾角α的增大，轴向与径向的跳动量误差也随之产生和增加。

3　轮毂回转偏心引起的误差

主轴回转中心与汽车轮毂几何中心不重合，产生回转偏心误差［3］，汽车轮毂实际中心为O，主轴的安装回转中心为A，所以偏心距为OA，如图4所示。

图4　轮毂回转偏心误差示意图

若忽略汽车轮毂径向跳动，测量时，径向跳动为零，测量点到轮毂实际中心距离为恒定值OB。由于偏心距OA，测量点到回转中心距离AB随转动角度w的变化而不断改变，这样，在测量过程中，由于定位安装偏心的存在就产生了径向跳动量。在△AOB中，根据余弦定理有：

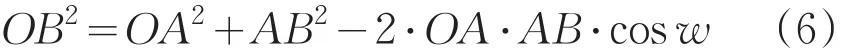
式（6）可转化为

其中，x=AB，a =OA，r =OB，根据求根公式且取“+”号：

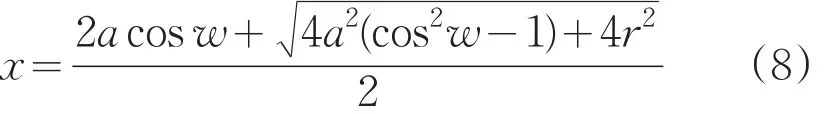
即

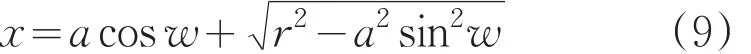
跳动量误差为

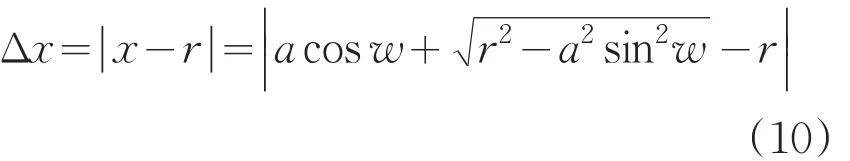
4　仿真与分析

图5　径向、轴向跳动随倾角α变化曲线

轮毂的径向跳动由于倾角α的存在，产生轴向的跳动分量；同理，轴向跳动也产生了径向跳动分量，这样，各个方向的跳动分量相互叠加，使检测结果有很大偏差。同时，这种偏差在测量数据中很难得到体现。图5可以看出，随着倾角α的变化，轴向跳动的变化与径向跳动相比更加明显。

取汽车轮毂半径r =256mm，偏心距a =1mm，应用Matlab进行仿真，得到转角w与中心距关系图像，如图6所示。

图6　转角w与中心距关系示意图

可以看出，偏心后中心距随转角增加，呈现类余弦曲线型，而且成周期性变化，这种变化与轮毂实际跳动量相互叠加，会使检测结果出现严重偏差。

由于车轮尺寸的不同，轮毂的径向、轴向跳动量检测标准也不同，根据汽车车轮跳动量的要求和检测方法，车轮轮毂径向、轴向跳动量要求分别在0.8mm和1.0mm内为合格［4］。检测系统为满足轮毂跳动量检测要求，设备旋转链接部件系统误差应满足：径向、轴向跳动量小于0.1mm，测量装置为精度在0.02mm以上的百分表或传感器，系统采用较为成熟的激光三角法测距法［5］，测量精度在0.01mm左右，满足测量要求［6］。

在测量中，误差往往是主轴垂直度和轮毂回转偏心共同引起的。主轴垂直度引起误差为Δx1，轮毂回转偏心引起径向误差为Δx2。因为Δx2由于倾角α引起的轴向分量很小，可忽略不计。取轮毂径向、轴向极限跳动量均为3mm，即x=3mm，y= 3mm，带入公式（5）得

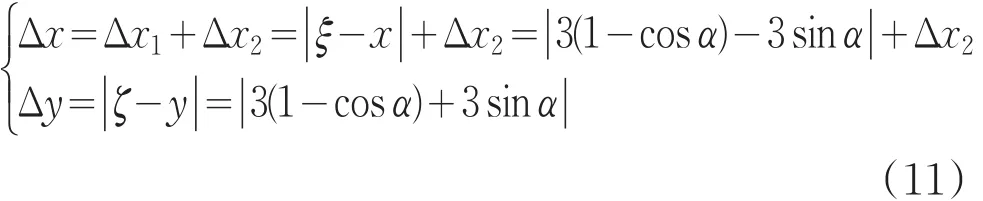
由Δy≤0.1，得

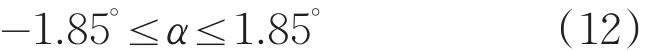
又因为回转偏心误差Δx2为系统安装误差，根据系统误差分配，取偏心误差的极限值，即令Δx2＜0.1mm/2=0.05mm，即计算得α范围：

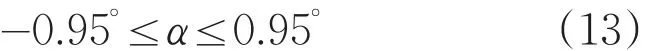
当-0.95∘≤α≤0.95∘时，主轴垂直度和轮毂回转偏心度所引起的误差之和小于0.1mm，这时，满足系统精度要求。

由以上分析得，系统的回转主轴垂直度以及轮毂安装偏心度引起系统测量误差：（1）随着倾角增大，轮毂径向、轴向跳动量之间，存在相互转化；（2）根据系统设计精度要求，回转主轴垂直度需通过装配调试进行调整，并控制在允许范围内；（3）轮毂安装偏心度所引起的误差是周期性的，增加了汽车轮毂的径向跳动量，应控制在系统误差范围以内。

5　结论

通过以上分析得出：检测系统的主轴垂直度、轮毂安装偏心度将引起较大的系统测量误差，可以根据系统误差分配，通过对系统精密装配、调整以减小误差，提高测量精度。文章为检测系统精密装配、调试提供了理论依据，对减小系统误差具有实际意义。

参考文献

［1］李海国.曲轴径向圆跳动误差的试验研究［J］.山东机械，2001，10（4）：12-23.

［2］马宏，王金波.仪器精度理论［M］.北京：北京航空航天大学出版社，2009：45-60.

［3］向胜梅.非连续回转面径向跳动量数据处理系统研究［D］.长春：长春理工大学，2008.

［4］天津车轮实验中心、天津汽车车轮有限公司.QC/ T717-2004汽车车轮跳动量的要求和检测方法［S］.北京：国家发展和改革委员会.2004.

［5］陈浩，吕超，车英，等.物面倾斜对激光三角法测量误差影响的分析研究［J］.长春理工大学学报：自然科学版，2015，38（1）：16-20.

［6］靳静力.圆柱齿轮径向跳动检测系统改进及误差补偿［D］.大连：大连理工大学，2005.

Analysis on Effect of Rotary Axis Perpendicular and Installation Eccentric to the Wheel Hub Runout Detection

LIU Zhongfu，WANG Zhenhong
（School of Mechatronical Engineering，Changchun University of Science and Technology，Changchun 130022）

Abstract：According wheel runout detection system，this paper analyzes the error sources affecting the system measurement accuracy. Through modeling and analyzing the errors caused by the structure，according to the structural principle，we get the rotation angle of the spindle hub radial，axial runout between function，and because wheel mounting radial eccentricity caused by the beating with the rotation angle of periodically varying functions. We verified the theory through the Matlab simulation and control variables. It provides a theoretical basis for assembling and installing the detection system，and it has practical significance in reducing systematic errors.

Key words：runout testing；verticality；rotary eccentric；error analysis

中图分类号：TP202

文献标识码：A

文章编号：1672-9870（2016）02-0035-04

收稿日期：2015-10-22

作者简介：刘忠夫（1990-），男，硕士研究生，E-mail：liuzf_438419216@126.com