岩层真厚度计算中负厚度的处理及其地质意义
2016-06-07朱正勇熊意林鲁显松杜翌超
朱正勇, 熊意林, 鲁显松, 胡 飞, 刘 嘉, 杜翌超
(湖北省地质调查院,湖北 武汉 430034)
岩层真厚度计算中负厚度的处理及其地质意义
朱正勇, 熊意林, 鲁显松, 胡 飞, 刘 嘉, 杜翌超
(湖北省地质调查院,湖北 武汉 430034)
以野外实测地质剖面在DGSInfo系统剖面库中的岩层真厚度计算结果出现负值及0值进行探讨,并与以列昂托夫斯基公式为厚度计算公式的结果进行对比分析,且对DGSInfo系统剖面库及列昂托夫斯基公式中岩层倾向与坡向的关系进行探讨,在此基础上,确认岩层厚度计算中负厚度识别及负号的应用,并厘定较为合理的岩层厚度计算公式和在计算岩层总厚度时较为科学的负值处理方法,进而对出现负厚度及0值厚度的原因进行分析,且对岩层负厚度所代表的地质意义作了较为详细地解释。
实测剖面;负厚度;sign值;DGSInfo;地质意义
1 概述
岩层真厚度计算为地质工作中最基础、最常见的工作之一,其计算结果的准确性事关众多地质问题的解决。自20世纪50年代引进列昂托夫斯基公式并使用至今,厚度计算公式形式变化多样,但其关键及难点问题始终为负厚度的识别和负号的应用。此文以野外剖面实测工作为基础,前人经验为参考,厘定较为科学、全面的岩层厚度计算公式,并对DGS系统中的负厚度和0值出现的原因进行分析及对岩层负厚度地质意义进行探讨。
2 理论基础
岩层厚度原始计算公式为20世纪50年代引进的列昂托夫斯基(简称“列氏”)公式[1],表述如下:
M=L(cosεsinβsinγ±sinεcosβ)
式中:M为某一测次所控制岩层真厚度;L为该测次的导线长度;ε为该测次导线之倾角(即地形坡角);β为该测次中岩层之倾角;γ为该测次中岩层走向与导线方向之间所夹正锐角。
其中0°<ε<90°,0°<β<90°,0°≤γ≤90°。
(当岩层倾向与地形坡向相反时,符号为正;当岩层倾向与地形坡向相同时,符号为负)。
上述公式引进较早,且发展至今在列昂托夫斯基公式基础上演变较多[2],如:①列氏公式的推导公式:实质为列氏公式在具体情况下的特殊形式[3-4];②何氏公式:中国科技工作者何昌祥(1990)对列氏公式的改进形式[5];③叶氏公式:中国科技工作者叶东户(1976)提出的“导线与岩层走向线的斜交”情况下的计算公式,与列氏公式没有亲缘关系,从形式到证明方法均具较强独特性[6];④其他公式:有关文献未进行证明或未注明出处,主要为具体情况下的计算公式。
上述公式对于某一单测次所控制的厚度绝对值均一致,且出现负厚度的情况,而负厚度是指实测剖面过程中,某一测次重复了的岩层厚度。据负厚度定义的内涵,拟定:导线从岩层下层面往上层面方向前进时所控制的岩层厚度为正厚度,从岩层上层面往下层面所控制的岩层厚度为负厚度[7]。前人在利用列氏公式计算岩层总真厚度时,对负厚度的处理方式各有不同,主要有如下几种选择:
(1)M=|A+B+…| 取各项代数和的绝对值。
(2)M=|A|+|B|+|C|+… 取各项绝对值的和。
(3)M=max{|A| or |B| or |C|+…} 取单项绝对值最大者(单层总厚)[8]。
(4)M=所有单项负数的绝对值的和,所有正数舍去(正值少时)[9]。
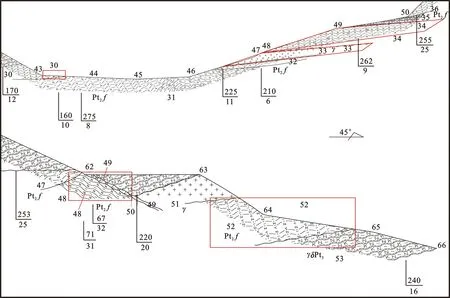
图1 湖北麻城福田河中元古界福田河岩组实测地层剖面PM09部分示意图(摘自湖北麻城福田河—白果镇地区矿产地质调查,2015年)
(5)M=所有单项正值的和,所有负数舍去(A、B、C代表岩层每一单测次的计算厚度)。
3 实例分析
以湖北省麻城市福田河中元古界福田河岩组实测地层剖面PM09为例,剖面上主体岩性为黑云二长花岗质片麻岩、黑云斜(二)长变粒岩及浅粒岩等,为大别山地区结晶基地上的一套老沉积盖层,其经历了多期多阶段的构造、变质变形等。因此,准确测定该区岩层真厚度较为重要。在DGSInfo系统剖面PM09数据库(表1)中,可知岩层单测次真厚度(表1中真厚度1)及单层总厚度均存在0值及负值的情形,而列氏计算公式结果亦有0值及负值的出现(表1中真厚度2)。
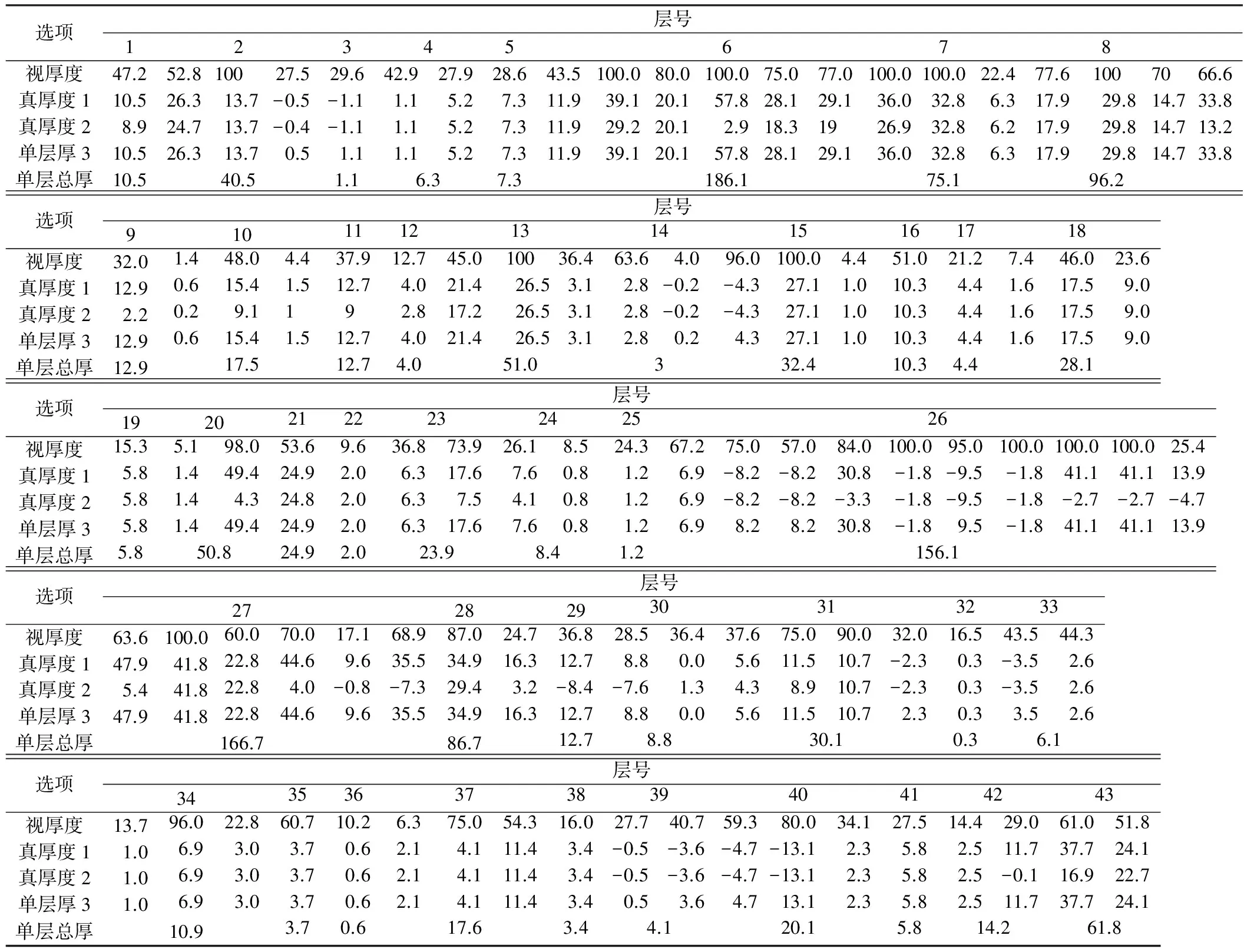
表1 DGSInfo、列氏计算公式、新厘定公式确定的剖面PM09岩层单测次厚度统计表
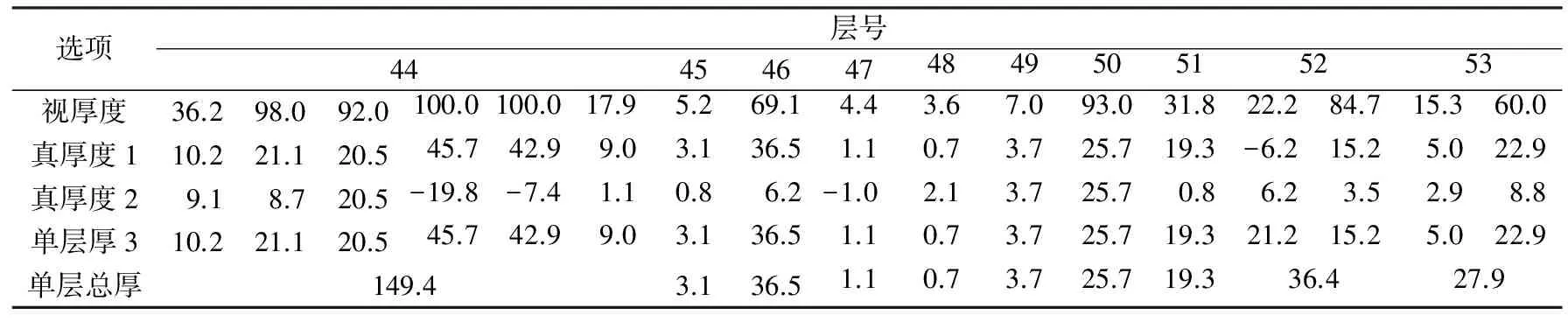
续表1
注:1)真厚度1为DGSInfo系统中剖面库自动生成;数据来源于项目《湖北麻城福田河—白果镇地区矿产地质调查》;2)真厚度2为列氏公式,D=L×(sinα×cosβ×cosγ±cosα×sinβ),sin(90°+(A-B))=COS(A-B)式中岩层倾向与地形坡向相反时用+号,反之用-号(常用);3)真厚度3为当岩层倾向与地形坡向相反:M=L(cosεsinβsinγ+sinεcosβ);4)当岩层倾向与地形坡向一致,且岩层倾角大于地形坡角,M=L|(cosεsinβsinγ-sinεcosβ)|;5)当岩层倾向与地形坡向一致,且岩层倾角小于地形坡角M=L(sinεcosβ-cosεsinβsinγ)。
在岩层真厚度计算时,DGSInfo系统剖面库和列氏公式中均涉及到岩层产状与坡向关系的探讨,在DGSInfo系统剖面库中自动生成sign值,对岩层倾向与坡向的关系进行定义。现将DGSInfo系统中自动生成的sign值、列氏公式生成的sign值列于表2,在表2中“1”代表岩层倾向与坡向相反,“-1”代表岩层倾向与坡向相同。PM09剖面中岩层片麻理产状为210°~240°∠12°~36°,剖面方位从起点到终点为45°,岩层倾向在剖面图中基本为左倾,另因坡角为负时地形线右倾(表2中绿色区,图1),坡角为正时地形线左倾(表2中黄色区,图1),因此,sign值为1时基本代表坡角为负值,sign值为-1时基本代表坡角为正值,且系统中默认坡角为0值时,sign值为1(表2中褐黄色区)。
在DGSInfo系统剖面库和列氏计算公式中,对sign值的判断均存在一定的错误。在表2及图1中,红色所代表的异常区,其中第30层红色异常区,根据野外实测和剖面图,坡向与倾向相反,应为正1,DGS判断错误;第33层红色异常区对应为一花岗岩脉,其产状左倾,与坡向相反,sign值为1正确;第34层红色异常区,对应的为一变粒岩,其产状局部发生变化,右倾,与坡向一致,为1,正确;第48层为一右倾的糜棱岩化片岩,与坡向倾斜方向一致,取-1;第52层红色异常区,岩层倾斜方向与坡角相反,应为1;第49层坡角为0°处,应为1。对上述错误修改后,重新厘定sign值,列于表2(见表2中sign3)。
因此,本文实测剖面中岩层真厚度的计算以列氏公式为基础,制定符合DGSInfo系统及野外实际的厚度计算公式如下:
当岩层倾向与地形坡向相反时,
M=L(cosεsinβsinγ+sinεcosβ)
(1)
当岩层倾向与地形坡向一致,且岩层倾角大于地形坡角时,
M=L|(cosεsinβsinγ-sinεcosβ|
(2)
当岩层倾向与地形坡向一致,且岩层倾角小于地形坡角时,
M=L(cosεsinβsinγ-sinεcosβ)
(3)
运用上述岩层厚度计算公式,重新计算剖面PM09岩层单测次厚度及单层总厚度,计算结果列于表1。
4 负厚度地质意义讨论
4.1 出现负厚度的情况分析
在DGS系统剖面分层数据库中,某一岩层单测次厚度指该测次的起点刻度到下一刻度处。而岩层真厚度计算中,负厚度是指实测剖面过程中,某一测次重复了的岩层厚度。据负厚度定义的内涵,导线从岩层下层面往上层面方向前进时所控制的岩层厚度为正厚度,从岩层上层面往下层面所控制的岩层厚度为负厚度。
现据实际经验,将出现负厚度的几种情况总结如下[10]:
(1) 导线前进方向与岩层倾向相同,坡向与倾向相同,|β|>α(图2中3-4导)。
(2) 导线前进方向与岩层倾向相反,坡向与倾向相反(图3中1-2导、3-4导)。
(3) 导线前进方向与岩层倾向相反,坡向与倾向相同,|β|<α(图4中0-1导)。
(β为地面坡度角,沿导线前进方向仰角为正,俯角为负;α为岩层在导线方向上的视倾角。)
上述(2)、(3)两种情况主要见于特殊剖面条件,即当岩层内揉皱造成局部倾向反向时,或当受地形障碍影响迫使导线突然反向前进时,只要把握住导线与上、下层面的关系,也不难识别负厚度。
图2为岩层露头不够良好的情况下测的剖面,对于某些岩性变化不大的岩层,常因被浮土掩盖而不易找到同一层面的对应点,在剖面导线平移也有困难的情形下,为了求得岩层的厚度,往往只好作连续的剖面丈量,可能有的测次是从岩层的下部向上部丈量(如图2中1-2导、2-3导、4-5导等),又有的测次是从岩层的上部向下部丈量(如图2中3-4导),这一上一下的测量,实际抵消了部分岩层厚度,会出现负值。
表2 DGSInfo、列氏公式、新厘定公式确定的剖面PM09岩层单测次的sign值统计表
Table 2 Statistical table of sign value of thickness of profile of PM09 strata by DGSInfo, Legalia calculation formula and new redefinition formula
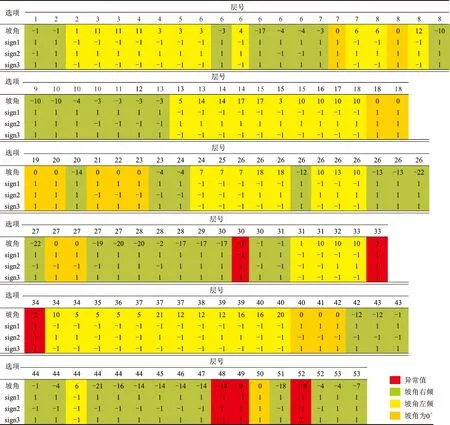
注:1)数据来源于《湖北麻城福田河—白果镇地区矿产地质调查》;2)sign1.DGSInfo系统剖面中分层库自动生成;sign2.列氏公式计算生成;sign3.依野外实际厘定;1.岩层倾向与坡向相反;-1.岩层倾向与坡向相同。
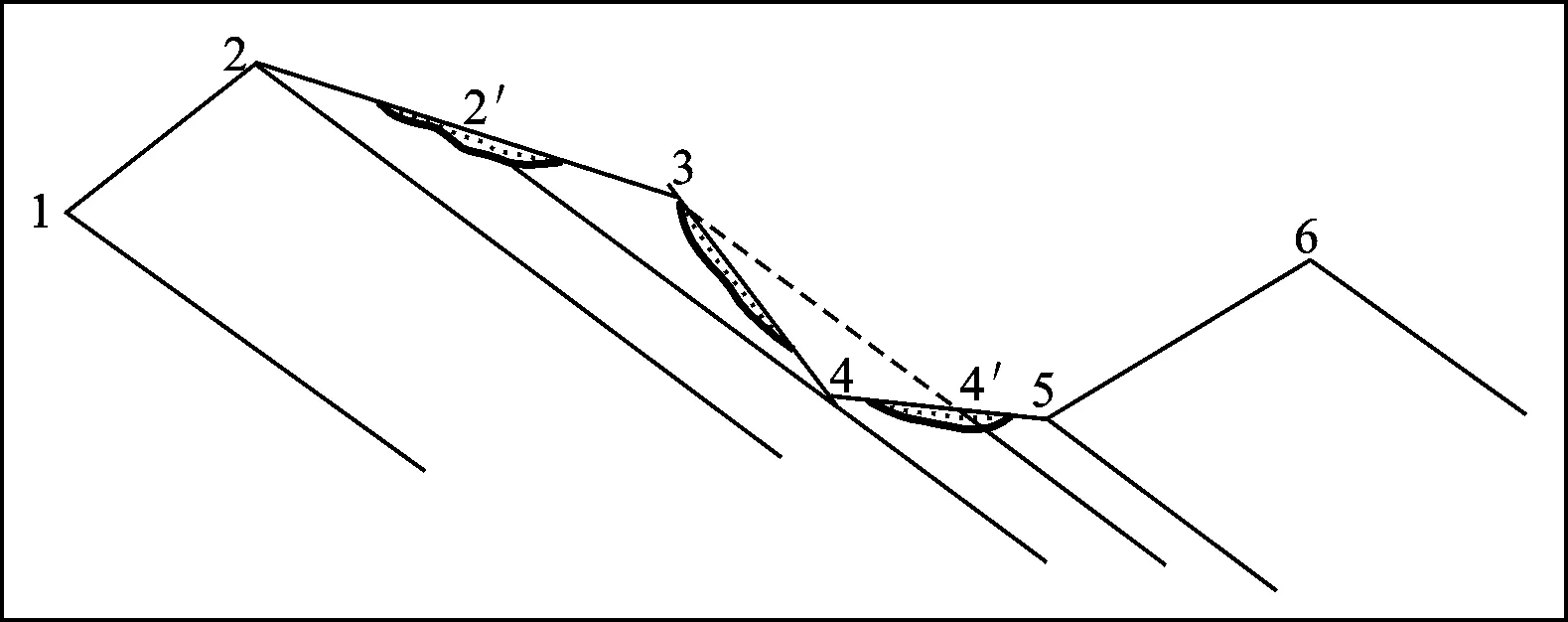
图2 实测剖面中导线前行方向与岩层方向相同,坡角小于和大于岩层倾角示意图(据文朴,1980)Fig.2 Schematic diagram of strata inclination of wire precession and strata in the same direction in measured section
图3中,岩层左倾,剖面方位向右,岩层单测次厚度分别为a1、b1、a2、b2,其中a1、a2为正数,b1、b2为负数,正数中a1代表岩层厚度。图4中,0-1导处,坡角小于视倾角时,岩层单测次厚度为负。
在某些较特殊的情况下,也会出现0值真厚度的情形,如:①工程线(剖面线)与岩(矿)层层面平行;②工程线(剖面线)与岩(矿)层走向平行。
4.2 地质意义解释
前人对于岩层真厚度计算中出现的负厚度作了简要的地质分析,本文结合野外剖面实测工作,对岩层厚度计算中可能出现负厚度的地质情况解释有:①地表长期剥蚀,造成局部地形变化;②局部地层揉皱反向;③实测时,因地形导致导线必须反向;④植被及覆盖物强、露头差时,对应层标志点未对应等。

图3 实测剖面中导线前进方向与岩层倾向相反,坡向与倾向相反时的示意图Fig.3 Schematic diagram of strata inclination of wire precession and strata in the opposite direction in measured section
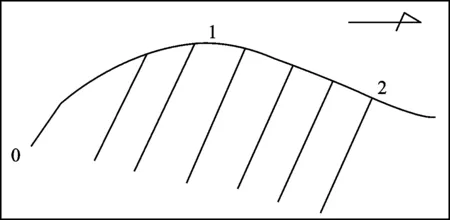
图4 实测剖面中导线前进方向与岩层倾向相反,坡向与倾向相同,坡角小于视倾角时示意图Fig.4 Schematic diagram of strata inclination of wire precession and strata in the opposite direction in measured section
5 小结
本文以野外实测剖面工作为基础,通过总结前人经验,得出以下几点结论:
(1) 合适的岩层厚度计算公式及负厚度处理方法,事关岩层厚度计算工作的成败。
(2) DGSInfo系统在计算岩层真厚度时,存在一定的不足,仍需地质人员结合野外实际进行判定。
(3) 负厚度不仅出现在实测剖面中,在钻孔、槽探、坑道等地质工程中计算岩(矿)层真厚度时,亦会出现此种情况,其处理方法相类似。
[1] 文朴.论岩层真厚度的计算方法[J].成都地质学院院报,1980(2):80-90.
[2] 徐少康.岩层真厚度计算的新公式[J].化工矿产地质,2006,28(4):209-217.
[3] 武汉地质学院,成都地质学院,南京大学地质系,等.构造地质学[M].北京:地质出版社,1979.
[4] 漆树基.利用袖珍计算器计算岩层真厚度[J].中国区域地质,1991(2):188-193.
[5] 何昌祥.岩层真厚度计算的改进公式[J].中国区域地质,1990(1):78-81.
[6] 叶东虎.岩层真厚度计算手册[M].北京:地质出版社,1976.
[7] 许边远.试用矢量表示岩层真厚度[J].中国区域地质,1998,17(1):80-86.
[8] 刘书才,杜圣贤,张贵丽.实测剖面地层厚度计算方法探讨[J].山东国土资源,2006,22(9):37-39.
[9] 朱显芝.关于地层真厚度计算公式的商酌[J].地质论评,1965,23(6):496-498.
[10] 郭福生,林银山.岩层真厚度计算公式的修正[J].江西地质,1992,6(3):280-286.
(责任编辑:陈文宝)
Discussion on Geological Significance and Treatment of Negative Thicknessin Calculation of the True Thickness of Strata
ZHU Zhengyong, XIONG Yilin, LU Xiansong, HU Fei, LIU Jia, DU Yichao
(HubeiGeologicalSurvey,Wuhan,Hubei430034)
According to the comparison of analysis about the negative thickness and the zero value of the calculation of the true thickness of strata appearing at the Digital Section System and the result calculating from Leon tibor scitovsky formula in a geological section, and the knowledge of mankind all clearly indicate the importance and difficulty in recognition and using of the negative sign about the calculation of the true thickness of strata. The paper detailedly analyses the value of “sign” from the Digital Section System and the Leon tibor scitovsky formula, in which “1” stands for the tendency of rock stratum is contrary to the slope, and “-1” stands for the tendency of rock stratum is same to the slope. Based on the above analyses, the paper formulates the reasonable calculation formulas and the scientific handling methods in negative thickness,analyses the geological meaning of the negative thickness.
measured section; negative thickness; value of “sign”; DGSInfo; geological meaning
2015-08-10;改回日期:2015-09-07
中国地质调查局中南地区地质调查项目基金资助项目,项目编号:12120114048401。
朱正勇(1987-),男,助理工程师,硕士,地质工程专业,从事矿床学研究和矿产普查与勘探工作。E-mail:339075731@qq.com
P624
A
1671-1211(2016)02-0217-05
10.16536/j.cnki.issn.1671-1211.2016.02.018
数字出版网址:http://www.cnki.net/kcms/detail/42.1736.X.20160303.1056.016.html 数字出版日期:2016-03-03 10:56
