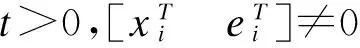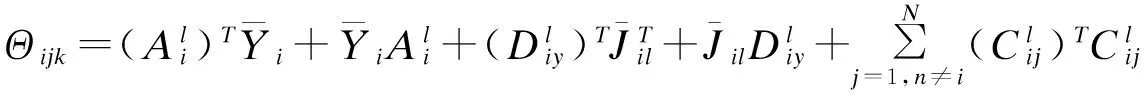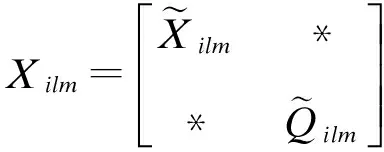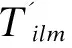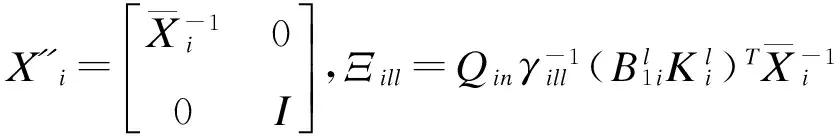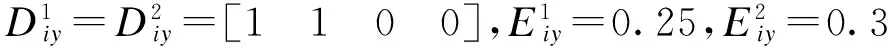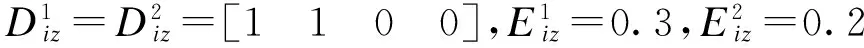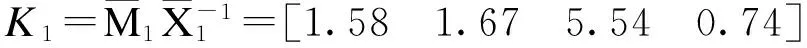基于T-S模糊模型的多机电力系统气门开度H∞控制

侯欣明，年佳琪，雷彦华，祝尚臻，于宏涛

(沈阳工程学院 自动化学院，辽宁 沈阳 110136)



基于T-S模糊模型的多机电力系统气门开度H∞控制

侯欣明，年佳琪，雷彦华，祝尚臻，于宏涛

(沈阳工程学院 自动化学院，辽宁 沈阳 110136)

摘要：针对多机电力系统气门开度的控制问题，构建了具有非线性关联作用的多机电力系统数学模型，并在T-S模糊模型局部线性化建模方法的基础上进行改进，提出了一种带有关联项的非线性系统的线性化模型。针对得到的T-S模糊模型，进行了基于观测状态的分散控制研究。最后通过Matlab进行仿真验证，结果证明所设计的多机电力系统线性化模型是可行、有效的。

关键词：多机电力系统；线性化模型；模糊分散控制

1多机电力系统的数学模型

考虑通过输电线连接的n台非中间再热式汽轮发电机组成的多机电力系统的气门开度控制问题，在T-S模糊模型局部线性化建模方法的基础上进行改进，提出一种带有关联项的非线性系统的线性化模型：

式中，xi(t)=

因实际运行的电力系统，并不是所有的状态变量都可用，根据并行分布补偿策略，对系统采用如下模糊控制器：

(2)

用如下模糊分散观测器来估计多机电力系统的状态：

(3)

(4)

式中，

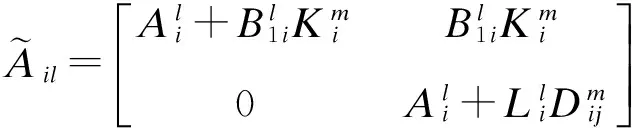
2多机电力系统控制

在分析和推导过程中，需要用到以下知识。

定义1如果下面2个条件满足，则连续时间互联大系统具有H∞性能指标γi。

1)当系统扰动为零时，闭环互联大系统系统渐近稳定；

2)当系统扰动为不零时，零初始条件如下：

式中，γi>0，i=1,…,J是给定干扰水平，其中zi是互联大系统第i个子系统的控制输出向量，ωi是互联大系统第个子系统的扰动向量。

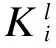
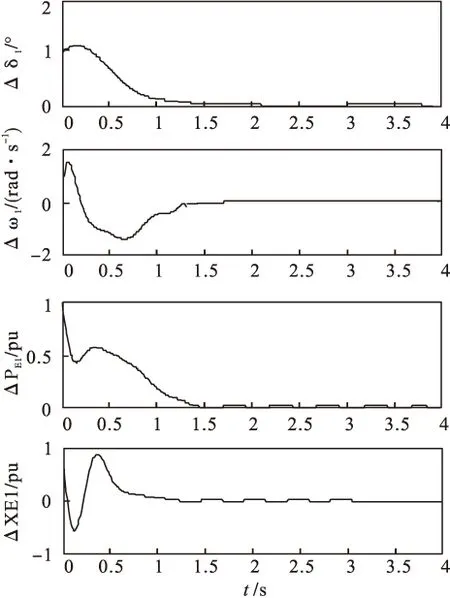
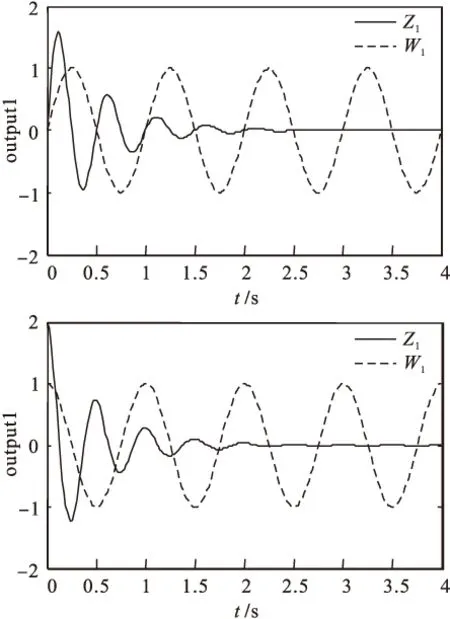
Ωill

(5)

Ωilm+Ωiml≤Xilm+Ximl,l≠m

(6)

(7)

其中，

为系统选择如下的Lyapunov函数：

对其求导，由(5)和(6)可知：

当wi≡0时，有

当wi≠0时，有

当x(0)=0时，V(x(0))=0，对0到∞两边求导得

下面由定理1推导出仅需一步就能解出的线性矩阵不等式。

(8)

(9)

(10)

(11)

(12)

(13)

式中，

j=1,2,…,N,j≠i.

首先证明定理1是定理2的充分条件。

至此，定理1是定理2的充分条件得以证明。接下来证明定理1是定理2的必要条件。

(14)

式中，

对其进行初等变换得到式(5)。对式(10)和式(11)运用Schur补定理，经过初等变换，通过做相同的变换，得到式(6)。

根据Schur补定理，由不等式(14)经过初等变换得到式(7)。

至此，定理1是定理2的充要条件得以证明。

3数据仿真

以2台发电机组成的互联系统为例来验证所设计的控制方案的有效性。取输出矩阵为

利用上面得到的控制器增益矩阵和观测器增益矩阵，对于给定的初始值x1(t)=x2(t)=[1111]T以及扰动w1(t)=sin(2πt)，w2(t)=cos(2πt)，基于观测状态的反馈控制后的发电机状态轨迹图如图1(1#发电机)和图2(2#发电机)所示，观测误差的轨迹图如图3(1#发电机)和图4(2#发电机)所示，系统输出曲线如图5所示。

图1　1#发电机的状态轨迹

图2　2#发电机的状态轨迹

从图3和4可以看出，2台发电机的气门开度控制增量的观测误差轨线在0.5 s左右就已经为0，它们输出的机械功率增量的观测误差轨线也在1.5 s左右变为0，而两者的转子角增量和相对角速度的观测误差轨线则在2 s才变为0。从图5可以看出，在存在扰动的情况下，系统在2 s左右趋于稳定。

图3　1#发电机的观测误差轨迹

从仿真结果图1和图2中可以看出，两台发电机的转子角增量、相对角速度和气门开度增量的轨线和输出的机械功率增量的轨线都在1.5 s左右就稳定下来，所有状态都无明显的低频振荡。

图4　2#发电机的观测误差轨迹

图5　1#发电机2#发电机的输出曲线

4结语

所进行在局部线性化建模方法的基础上给出了多机电力系统气门开度控制的线性化模型，研究了基于观测状态的分散控制器的设计问题。基于T-S模糊模型给出了多机电力系统具有H∞性能指标的稳定条件，在此基础上给出线性矩阵不等式(LMIs)条件，并且给出各增益矩阵的求解算法，减小了条件的保守性。 仿真结果表明施加一定的控制后，所有状态都很快被镇定，这进一步验证了所设计的控制器是可行、有效的。

参考文献

[1]孙妙平,年晓红,潘欢.具有扇形执行器的多机电力系统气门开度的时滞无关镇定[J].控制理论与应用，2012，29(12)：1661-1668.

[2]张敏,蔡创文,刘伟,等.包含静止无功发生器的电力系统鲁棒H∞控制[J].电工电能新技术，2011，30(3)：19-23.

[3]于宏涛，李丽霞，祝尚臻.用改进蚁群算法制定电力线路检修计划[J].沈阳工程学院学报：自然科学版，2009,5(1):44-47.

[4]Wu J L.Robust H∞control for polytopic nonlinear control systems [J]. IEEE Trans,2013,11(58): 2957-2962.

[5]Mazenc F,Ito H.Lyapunov technique and back stepping for nonlinear neutral systems [J]. IEEE Transactions on Automatic Control,2013,58(2): 512-517.

[6]吴忠强,姚源,窦春霞.多机电力系统模糊自适应控制[J].电力系统保护与控制，2011，39(10)：5-10.

[7]孙妙平,年晓红,潘欢.基于观测器的汽轮发电机气门开度的时滞无关控制[J].控制理论与应用，2012，29(5)：593-598.

[8]Wu J L.RobustH∞control for polytopic nonlinear control systems [J].IEEE Trans,2013,11(58): 2957-2962.

(责任编辑佟金锴校对张凯)

Steam Valve Opening Control of Multi-Machine Power System Based on T-S Fuzzy Model

HOU Xin-ming,NIAN Jia-qi,LEI Yan-hua,ZHU Shang-zhen,YU Hong-tao

(School of Automation,Shenyang Institute of Engineering,Shenyang 110136,Liaoning Province)

Abstract：Focused on the steam valve opening control,this paper presented a linear model for nonlinear systems with interconnections based on the improved local linear T-S fuzzy model of the multi-machine power systems with nonlinear correlation function. Decentralized control of the model under the observation condition was proposed. Matlab simulation verified the feasibility and validity of this model.

Key words：Multi-Machine Power System;Linearization Model;Observer Decentralized Fuzzy Robust

中图分类号：TP13

文献标识码：A

文章编号：1673-1603(2016)02-0153-06

DOI：10.13888/j.cnki.jsie(ns).2016.02.013

作者简介：侯欣明(1989-)，女，河北唐山人，助理工程师，硕士。

收稿日期：2015-09-18