基于短时傅里叶变换与相关解调的参数估计算法
2016-06-06邹金龙
燕 天,洪 飞,邹金龙,马 捷
(1.机电动态控制重点实验室,陕西 西安 710065;2.西安现代控制技术研究所,陕西 西安 710065)
基于短时傅里叶变换与相关解调的参数估计算法
燕天1,洪飞2,邹金龙1,马捷1
(1.机电动态控制重点实验室,陕西 西安 710065;2.西安现代控制技术研究所,陕西 西安 710065)
摘要:针对傅里叶变换无法估计对称三角线性调频连续波信号的调制周期,短时傅里叶变换参数估计精度低的问题,提出了基于最佳频率分辨率窗宽的高斯窗短时傅里叶变换与改进的相关解调相结合的参数估计算法。该算法首先使用基于瞬时频率的窗宽倍增搜索算法获取最佳频率分辨率窗宽,其次使用高斯窗短时傅里叶变换求得对称三角线性调频连续波信号的中心频率和调制带宽,再使用改进的相关解调求出信号的调频斜率,进而求出信号的调制周期。仿真结果表明:本文算法不但提高了短时傅里叶变换对于对称三角线性调频连续波信号中心频率,调制带宽和调制周期的估计精度,而且具备良好的实时性。
关键词:数字信号处理;对称三角线性调频连续波;参数估计;短时傅里叶变换;相关解调
0引言
近年来,国内外学者针对对称三角线性调频连续波(Symmetrical Triangular Linear Frequency Modulation Continuous Wave,STLFMCW)信号的参数估计问题进行了大量的研究。文献[1]提出一种基于(RAT,Radon-Ambiguity)变换与分数阶傅里叶变换相结合的参数估计算法,该算法相比于采用二维搜索的Radon-Wigner变换法,以较小的运算量实现了对信号初始频率的估计,但利用RAT变换估计信号调频斜率的运算量非常大。文献[2]提出一种分数阶傅里叶变换与聚类分析相结合的参数估计算法,该算法克服了信号尖峰必须高于噪声幅度的限制,可以实现低信噪比条件下信号的检测与参数估计,但该算法要求截获信号的起点位于调频周期的起点,因此不适合无先验知识的信号参数估计。文献[3]采用高阶累积量与多相滤波器组相结合的算法实现对信号的参数估计,该算法无需先验知识且能较好地抑制高斯噪声,然而该算法的估计精度会随着多相滤波器组数的增加而下降。文献[4]提出一种基于瞬时频率的窗宽匀速搜索算法,该算法能够根据信号特征自主调节短时傅里叶变换的窗宽且对噪声不敏感,但该算法搜索速度很慢。文献[5]提出一种基于相关解调、解线性调频和最大似然估计的参数估计算法,估计精度较好,但仅适用于线性调频信号的参数估计且引入最大似然估计校正精度,运算量非常大。本文针对文献[4]、文献[5]算法存在的不足进行了改进,提出了基于最佳频率分辨率窗宽的高斯窗短时傅里叶变换与改进的相关解调相结合的STLFMCW信号参数估计算法。
1基于短时傅里叶变换的非平稳信号参数估计算法
1.1基于瞬时频率的窗宽匀速搜索算法
文献[4]提出了基于瞬时频率的窗宽匀速搜索算法,该算法步骤如下:
1)选定初始窗宽L0=l0,起始时刻τ,瞬时频率偏差ε,求出L0内信号的瞬时频率f0=f(t-τ,L0)。
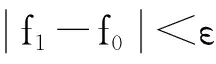
算法流程如图1所示。
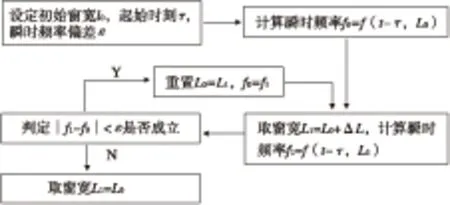
图1 基于瞬时频率的窗宽匀速搜索算法Fig.1 Window width uniform velocity search algorithm based on instantaneous frequency
1.2基于相关解调、解线性调频和最大似然估计的参数估计算法
文献[5]提出了基于相关解调和解线性调频的参数估计算法,该算法首先利用相关解调求出线性调频(LinearFrequencyModulated,LFM)信号调频斜率的粗略估计值,其次对LFM信号解线性调频并作短时傅里叶变换,求出LFM信号初始频率的粗略估计值,最后在时频平面进行局部最大似然搜索,求出调频斜率和初始频率的精确估计值。算法流程如图2所示。
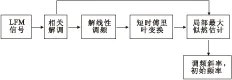
图2 基于相关解调和解线性调频的参数估计算法Fig.2 Parameters estimation algorithm based on correlation demodulation and relieving linear frequency
2参数估计算法原理
本文算法首先根据时频分析的目的,选择短时傅里叶变换窗函数,其次使用基于瞬时频率的窗宽倍增搜索算法求出最佳频率分辨率窗宽,然后对STLFMCW信号进行短时傅里叶变换,求出信号的最小频率fmin,最大频率fmax,以及首次出现最小频率的时刻tmin和首次出现最大频率的时刻tmax,根据fc=0.5·(fmax+fmin)求出信号的中心频率fc,根据ΔF=(fmax-fmin)求出信号的调制带宽ΔF,再使用改进的相关解调算法,求得STLFMCW信号的调频斜率k,根据T=2ΔF/k求出信号的调制周期T。算法流程如图3所示。
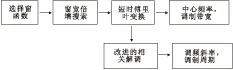
图3 基于短时傅里叶变换与相关解调的参数估计算法Fig.3 Parameters estimation algorithm based on STFT and correlation demodulation
2.1选择窗函数
对非平稳信号进行时频分析,需要窗函数具备尽量小的时频分辨率乘积和较高的时频聚集性,根据Heisenberg不确定性原理,时频分辨率乘积不小于0.5,而采用高斯窗函数,时频分辨率的乘积可以取到不确定性原理的下限0.5,因此高斯窗函数具有最佳的时频分辨率。又因为高斯窗函数的傅里叶变换依然是高斯的,所以信号时域和频域的能量都较为集中,故本文选择高斯窗函数。
2.2基于瞬时频率的窗宽倍增搜索算法
本文采用高斯窗短时傅里叶变换对STLFMCW信号的中心频率和调制带宽进行估计,对频率分辨率要求较高。因此需要在保证信号局部平稳的前提下,尽量增大窗宽,本文提出一种基于瞬时频率的窗宽倍增搜索算法,算法框图如图4所示。
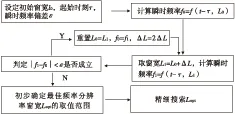
图4 基于瞬时频率的窗宽倍增搜索算法Fig.4 Window width doubly velocity search algorithm based on instantaneous frequency
相比于窗宽匀速搜索算法,本算法将窗宽增幅不断翻倍,先初步确定最佳频率分辨率窗宽的取值范围,再精细搜索最佳频率分辨率窗宽,算法具体步骤如下:
1)选定初始窗宽L0=l0,起始时刻τ,瞬时频率偏差ε,求出L0内信号的瞬时频率f0=f(t-τ,L0)。
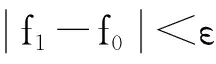
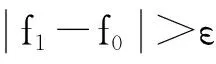
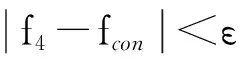
考虑到信号频谱结构发生改变而瞬时频率不变的情况,对窗宽倍增迭代次数n设定上限n=20,则本算法共需进行(2n-1)次搜索。不难验证,本算法的搜索次数和运算量远小于窗宽匀速搜索算法。通过上述搜索算法获得的窗宽是满足信号局部平稳要求的最大窗宽,具有最佳的频率分辨率。使用最佳频率分辨率窗宽Lopt进行短时傅里叶变换,求得信号的中心频率fc和调制带宽ΔF。
2.3改进的相关解调
对具有固定调频斜率的线性调频信号可以直接采用相关解调估计调频斜率,但STLFMCW信号的调频斜率是时变的,因此无法直接使用相关解调估计调频斜率。必须先搜索STLFMCW信号的线性调频段,再使用相关解调进行参数估计,算法步骤如下:
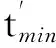
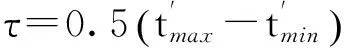
3运算量分析与仿真验证
3.1运算量分析
短时傅里叶变换通常用于信号的实时处理中,本文算法对短时傅里叶变换进行了改进,现对算法的运算量进行分析。
首先对窗宽倍增搜索算法的运算量进行分析。假定窗宽倍增迭代次数为n,则进行(2n-1)次搜索后可得到最佳频率分辨率窗宽Lopt。设初始窗宽l0内信号点数为q0,第m次搜索得到的窗宽内信号点数为qm,使用快速傅里叶变换计算信号频谱,则搜索最佳频率分辨率窗宽需进行Qall次运算:
(1)
若信号采样点数为N,以最佳频率分辨率窗宽Lopt进行短时傅里叶变换,设步长为a,则对信号进行短时傅里叶变换需进行V次运算:
(2)
因为n≤20,2n-1≪N/a,所以窗宽倍增搜索算法的运算量远小于短时傅里叶变换本身的运算量。
其次对改进的相关解调算法的运算量进行分析。设一个调制周期内信号点数为I,令D=0.25I,则改进的相关解调算法的运算次数G为:
(3)
通常信号采样点数N≥5I,当N=5I时,短时傅里叶变换的运算次数V为:
(4)
因为a (5) 因此V≫G,即相关解调的运算量相比于短时傅里叶变换本身的运算量非常微小。 综上所述,本文算法的运算量与短时傅里叶变换相比并无显著增加,适用于信号的实时处理。 3.2实验仿真 给定三组STLFMCW输入信号: 信号1:中心频率fc=270MHz,调制带宽ΔF=40MHz,调制周期T=20μs,采样率fs=1160MHz,构造一段长度为5个周期的STLFMCW信号来进行参数估计。 信号2:中心频率fc=290MHz,调制带宽ΔF=30MHz,调制周期T=30μs,采样率fs=1220MHz,构造一段长度为5个周期的STLFMCW信号来进行参数估计。 信号3:中心频率fc=310MHz,调制带宽ΔF=20MHz,调制周期T=40μs,采样率fs=1280MHz,构造一段长度为5个周期的STLFMCW信号来进行参数估计。 仿真时加入高斯白噪声,令信噪比从0~20dB,均使用高斯窗函数,每个信噪比进行1000次蒙特卡洛实验,采用归一化均方误差(NRMSE)作为误差衡量标准。 根据窗宽倍增搜索方案,求出信号1的最佳频率分辨率窗宽L1=0.9μs,信号2的最佳频率分辨率窗宽L2=1.3μs,信号3的最佳频率分辨率窗宽L3=1.7μs。 图5分别给出了不同信噪比下,采用不同窗宽时,信号1,信号2,信号3中心频率的估计误差;图6分别给出了不同信噪比下,采用不同窗宽时,信号1,信号2,信号3调制带宽的估计误差。 由仿真结果可知,在相同信噪比下,使用最佳频率分辨率窗宽Lopt进行短时傅里叶变换与使用其它固定窗宽进行短时傅里叶变换相比,中心频率的估计误差大幅降低,调制带宽的估计误差降低了一个数量级。令Δl(Δl>0)为最佳频率分辨率窗宽Lopt的微小偏移量,当窗宽L=Lopt±Δl时,中心频率和调制带宽的估计误差明显增大。Δl取值越大,中心频率和调制带宽的估计误差增幅越大。 图5 信号中心频率的估计误差Fig.5 Error curve of the center frequency 图6 信号调制带宽的估计误差Fig.6 Error curve of the modulation bandwidth 在同一运算平台下,对信号1,信号2,信号3均使用最佳频率分辨率窗宽,采用高斯窗短时傅里叶变换和本文算法各进行100次参数估计。两种算法对于调制周期的估计误差如图7所示,两种算法的运算时间如图8所示。 仿真结果表明,当信噪比大于0 dB且均使用最佳频率分辨率窗宽时,采用高斯窗短时傅里叶变换与改进的相关解调相结合的参数估计算法相比于仅采用高斯窗短时傅里叶变换的参数估计算法,运算时间增加了10%左右,调制周期的估计误差降低了30%左右。 图7 信号调制周期的估计误差Fig.7 Error curve of the modulation period 图8 信号的参数估计时间Fig.8 Parameters estimation time 4结论 本文提出了基于最佳频率分辨率窗宽的高斯窗短时傅里叶变换与改进的相关解调相结合的参数估计算法。该算法首先利用基于瞬时频率的窗宽倍增搜索方案求出最佳频率分辨率窗宽,大幅减小了窗宽匀速搜索方案的运算量,其次使用基于最佳频率分辨率窗宽的高斯窗短时傅里叶变换法估计对称三角线性调频连续波信号的中心频率和调制带宽,再使用改进的相关解调法重新估计调制周期,有效地缓解了短时傅里叶变换法时频分辨率相互制约的矛盾。仿真结果表明,在相同信噪比条件下,本文算法相比于使用其它固定窗宽的高斯窗短时傅里叶变换法,对中心频率和调制带宽的估计误差大幅降低;当信噪比大于0 dB且均使用最佳频率分辨率窗宽时,相比于仅采用高斯窗短时傅里叶变换的参数估计算法,本文算法的运算时间仅增加了10%左右,而调制周期的估计误差降低了30%左右。 参考文献: [1]袁伟明,王敏,吴顺君.对称三角线性调频连续波信号的检测与参数估计[J].电波科学学报,2005,20(5):594-597. [2]刘锋,徐会法,陶然.基于FRFT的对称三角线性LFMCW信号检测与参数估计[J].电子与信息学报,2011,33(8):1864-1870. [3]冯志红,赖涛,赵拥军.低信噪比下对称三角线性调频信号参数估计[J].电波科学学报,2012,27(3):520-525. [4]李允公,姚兆,刘杰,等.基于瞬时频率的窗宽递增寻优的短时傅里叶变换[J].东北大学学报,2007,28(12):1005-3026. [5]华旭东,臧小刚,唐斌.一种线性调频信号参数估计实时系统的设计[J].信息技术,2007,25(7):1009-2552. Parameters Estimation Based on Short Time Fourier Transform and Correlation Demodulation YAN Tian1,HONG Fei2, ZOU Jinlong1, MA Jie1 (1.Science and Technology on Electromechanical Dynamic Control Laboratory,Xi’an 710065,China2.Xian Advanced control Technologies Research Institute, Xi’an 710065,China) Abstract:Aiming at the problem that Fourier transform couldn’t estimate the modulation period of symmetrical triangular linear frequency modulation continuous wave (STLFMCW) signal, and short time Fourier transform (STFT) couldn’t estimate parameters accurately, an estimation method based on optimal frequency resolution ratio gauss window width STFT and improved correlation demodulation was proposed. Firstly, the method acquired the optimal frequency resolution ratio window width through the measure of window width doubly searching, and then made use of the gauss window STFT to obtain the STLFMCW signal’s center frequency and the modulation bandwidth. Then for the purpose of attaining the signal’s modulation period,the method got the signal’s frequency modulation gradient by means of the improved correlation demodulation. MATLAB simulation indicated that the method could improve the STFT parameters estimation precision in a short time. Key words:digital signal process;STLFMCW;parameters estimation;STFT; correlation demodulation 中图分类号:TN911 文献标志码:A 文章编号:1008-1194(2016)02-0018-05 作者简介:燕天(1989-),男,陕西西安人,硕士研究生,研究方向:通信与信息系统。E-mail:793194605@sina.com。 *收稿日期:2015-12-21