Frechet空间上移位算子的强specification－性质

周光亚

Frechet空间上移位算子的强specification－性质

周光亚

(四川工程职业技术学院，四川德阳618000)

证明定义在具有无条件基的Frechet空间上的移位算子是Devaney混沌的，当且仅当其具有强specification－性质，从而推广文献(S．Bartoll S，F．Martinez－Gimenez，A．Peris．J Diff Eqns Appl，2012，18: 599－605．)的主要结果到Frechet空间．

specification－性质;Devaney混沌;移位算子;Frechet空间

1 基本定义

设(X，d)是一个完备的度量空间，映射f:X→X连续，则称(X，f)为一动力系统．本文中，令N={1，2，…，n}，Z={…，－1，0，1，…，n}并且Z+={0，1，2，…，n}．文献［1］首次给出了混沌的精确数学定义，即为大家熟知的Li－Yorke混沌．R．L．Devaney［2］从系统的遍历性和敏感性出发，给出了另一种为大家普遍接受的混沌定义—Devaney混沌．

称动力系统(X，f)是Devaney混沌的，如果其满足以下条件:

1)f是拓扑传递的，即对任意非空开子集U，V X，存在n∈Z+，使得fn(U)∩V≠ ;

2)f的周期点在X中稠密;

3)f是初值敏感依赖的，即存在ε＞0，使得对任意x∈X及δ＞0，有n∈Z+及y∈X满足d(x，y)＜δ，使得d(fn(x)，fn(y))＞ε．

值得注意的是，J．Banks等［3］证明周期点稠密的拓扑传递系统是初值敏感依赖的;W．Huang等［4］得到含周期点的拓扑传递系统是Li－Yorke混沌的;特别地，Devaney混沌蕴含Li－Yorke混沌．

Specification－性质源于文献［5］关于公理A－微分同胚的研究，并且后来得到了众多学者的广泛研究［5－17］．

定义1［5］在紧度量空间(X，d)上的连续映射f:X→X具有强specification－性质，如果对任意δ＞ 0，存在Nδ∈N，使得对任意s≥2，{y1，y2，…，ys} X及整数0=j1≤k1＜j2≤k2＜…＜js≤ks满足 jr+1－kr≥Nδ(0≤r≤s－1)，存在x∈X，使得对任意r≤s及jr≤i≤kr，以下条件成立:

1)d(fi(x)，fi(yr))＜δ;

2)fNδ+ks(x)=x，特别地，如果以上条件对s=2成立，则称(X，f)具有弱specification－性质．

为研究Banach空间上有界线性算子的specification－性质，S．Bartoll等［6］最近将该定义推广到Banach空间;同时得到可分Banach空间上的移位线性算子具有specification－性质当且仅当它是Devaney混沌的．作为自然推广，首先将specification－性质的定义推广到 Frechet空间;同时得到可分Frechet空间上移位算子specification－性质的一些等价刻画．

定义2 设X为Frechet空间．称有界线性算子T:X→X具有(强)specification－性质，如果存在递增的T－不变紧子集序列{Km}m∈N满足0∈K1并且使得对任意 m∈N，T|Km具有(强) specification－性质．

2 移位算子的强specification－性质

对于正数序列(vn)n∈N(亦称权序列)，考虑如下的Banach空间:

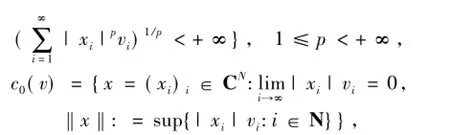
定义其上的移位算子B为B((xi)i)=(xi+1)i．

同理，对于正数序列(vn)n∈Z，考虑定义在 Banach空间

上的移位算子B为B((xi)i)=(xi+1)i．

对以上定义的移位算子，S．Bartoll等［6］得到了如下结果．

定理1［6］设B为定义在lp(v)(或者c0(v))上的有界移位算子，则以下命题等价:

2)B是Devaney混沌的;

3)B具有强specification－性质．

定理2［6］设B为定义在lp(v，Z)(或者c0(v，Z))上的有界移位算子，则以下命题等价:

2)B是Devaney混沌的;

3)B具有强specification－性质．

作为 Banach空间的自然推广，本文考察Frechet空间上移位算子的specification－性质．虽然得到的结果与Banach空间很平行，但是本文的证明方法和文献［6］是截然不同的，因为Frechet空间上移位算子的动力性质更为复杂，同时不难发现，文献［6］的结果只是本文定理的直接推论．

设X为向量空间，(‖·‖n)n∈N为定义在X上的递增的半范序列，则称X为一个Frechet空间．定义空间X上的完备F－范数‖·‖为

如果对任意x∈X，存在唯一的系数xn∈C，使得则称序列{en}n∈N为空间X的一组基底．

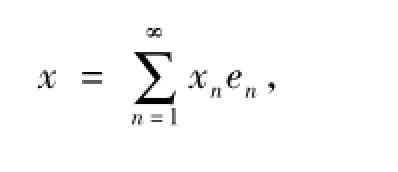
称Frechet空间X的基底{en}n∈N为无条件基，如果对任意x∈X，级数x=无条件收敛．

定理 3 设 X为 Frechet序列空间，并且{en}n∈N为X的无条件基．定义移位算子B:X→X为

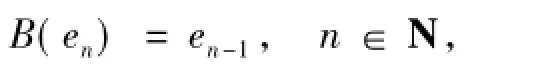
其中e0:=0，以下命题等价:

1)在X中收敛;

2)B是Devaney混沌的;

3)B具有强specification－性质;

4)B具有弱specification－性质．

证明 由文献［18］及specification－性质的定义可得3)→4)→1) 2)，因此，只需证明:1)→3)．

对任意m∈N，取Km={ n∈N}．显然，Km为空间X的B－不变子集，并且

断言1 Km为紧致子集．

断言2 B|Km具有强specification－性质．

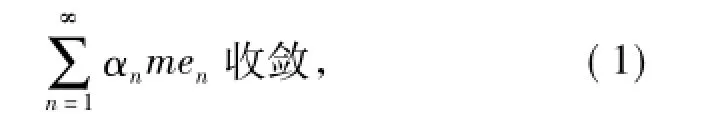
并且

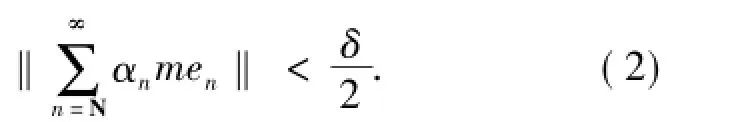
由(2)式可得，对任意序列{zn∈C:|zn|≤m}n∈N及任意K≥N，

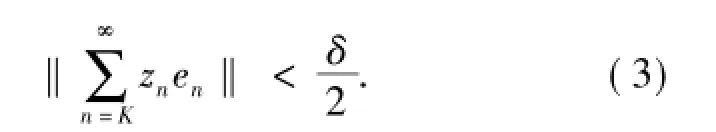
令Nδ=N+1．对{y1，y2，…，ys} Km及任意整数0 =j1≤k1＜ j2≤k2＜… ＜ js≤ks满足jr+1－kr≥Nδ(1≤ r≤ s－1)，不是一般性，假设 yr=．取x=如下

显然，x∈Km并且Bks+Nδ(x)=x．

对任意1≤r≤s－1及任意jr≤n≤jr+1－1，不难验证:，由此结合(3)式，同时注意到≤m 并且 jr+1－kr≥ Nδ，自然可得对任意jr≤i≤kr有

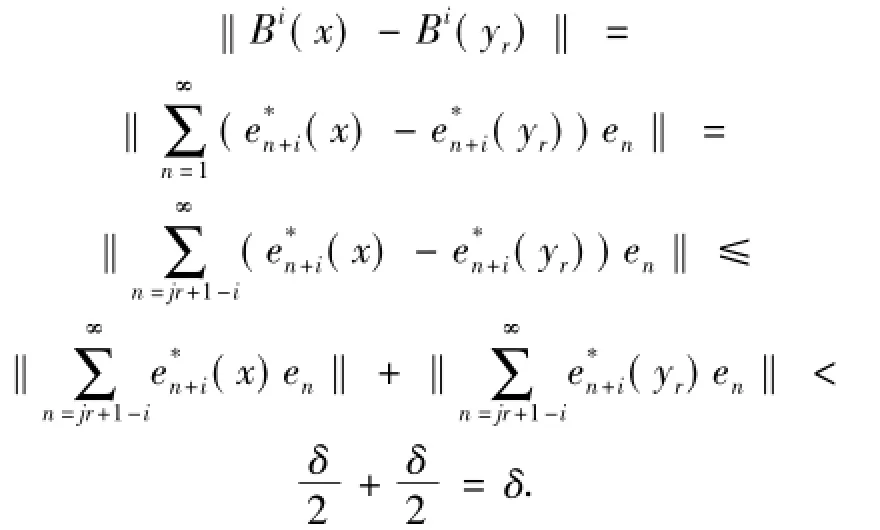
同理，对任意js≤i≤ks有

定理 4 设 X为 Frechet序列空间，并且{en}n∈Z为X的无条件基．定义移位算子B:X→X为

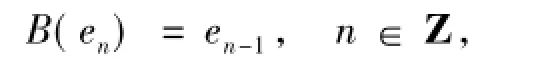
则以下命题等价:

2)B是Devaney混沌的;

3)B具有强specification－性质;

4)B具有弱specification－性质．

证明 由文献［18］，只需证明1) 3)．

对任意m∈N，取B－不变的紧子集Km=．任意给定δ＞0，注意到{en}n∈Z为无条件基，所以存在N∈N，使得对任意序列{zn∈C:|zn|≤m}n∈Z及任意K≥N，

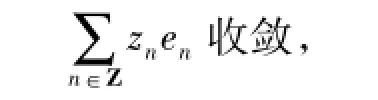
并且

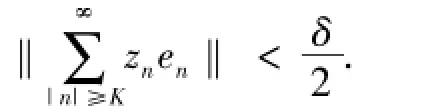
令Nδ=2N+1．对{y1，y2，…，ys} Km及整数0= j1≤k1＜j2≤k2＜… ＜js≤ks满足jr+1－kr≥Nδ(1≤r≤s－1)，置yr=，同时取x =如下

显然，x∈Km并且Bks+Nδ(x)=x．类比于定理3的证明，不难验证:B|Km具有强specification－性质．

同于文献［18］和定理3、4，以下结果显然成立:

定理 5 设 X为 Frechet序列空间，并且{en}n∈N为X的一组无条件基．定义权移位算子Bw: X→X为

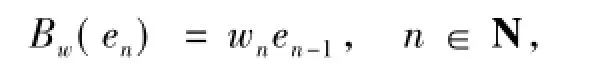
其中e0:=0，并且权值w={wn}n∈NC{0}，则以下命题等价:

1)在X中收敛;

2)Bw是Devaney混沌的;

3)Bw具有强specification－性质;

4)Bw具有弱specification－性质．

定理6 设X为Frechet序列空间，并且{en}n∈Z为X的无条件基．定义权移位算子Bw:X→X为

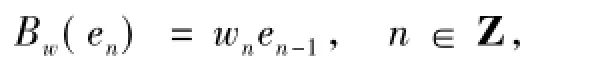
其中权序列w={wn}n∈ZC{0}，则以下命题等价:

1)在X中收敛;

2)Bw是Devaney混沌的;

3)Bw具有强specification－性质;

4)Bw具有弱specification－性质．

定理5自然可得以下推论:

推论 1 设 Bw为定义在 Kothe序列空间λp(A)(1≤p＜+∞，或者p=0)上的连续权移位算子，则以下命题等价:

2)Bw是Devaney混沌的;

3)Bw具有强specification－性质;

4)Bw具有弱specification－性质．

［1］LI T Y，YORKE J A．Period three implies chaos［J］．Am Math Monthly，1975，82:985－992．

［2］DEVANEY R L．An Introduction to Chaotic Dynamical Systems［M］．Redwood Providence:Addison－Wesley，1989．

［3］BANKS J，BROOKS J，CAIRNS G，et al．On Devaney’s definition of chaos［J］．Am Math Monthly，1992，99:332－334．

［4］HUANG W，YE X D．Devaney’s chaos or 2－scattering implies Li－Yorke’s chaos［J］．Topology Appl，2002，117:259－272．

［5］BOWEN R．Topological Entropy and Axiom A［M］．Am Math Soc，1970:23－41．

［6］BARTOLL S，MARTINEZ－GIMeNEZ F，PERIS A．The specification property for backward shift［J］．J Diff Eqns Appl，2012，18:599－605．

［7］BAUER W，SIGMUND K．Topological dynamics of transformations induced on the space of probability measures［J］．Monatsh Math，1975，79:81－92．

［8］KULCZYCKI M，KWIETNIAK D，OPROCHA P．On almost specification and average shadowing properties［J］．Fund Math，2013，224(3):241－278．

［9］OPROCHA P．Specification properties and dense distributional chaos［J］．Disc Contin Dyn Syst，2007，17:821－833．

［10］OPROCHA P，STEFANKOVA M．Specification property and distributional chaos almost everywhere［J］．Proc Am Math Soc，2008，136:3931－3940．

［11］WU X，OPROCHA P，CHEN G．On various definitions of shadowing with average error in tracing［J］．Nonlinearity，2016，29: 1942－1972．

［12］SAKAI K，SUMI N，YAMAMOTO K．Diffeomorphisms satisfying the specification property［J］．Proc Am Math Soc，2010，138: 315－321．

［13］WANG H，WANG L D．The weak specification property and distributional chaos［J］．Nonlinear Analysis，2013，91:46－50．

［14］WU X．Li－Yorke chaos of translation semigroups［J］．J Diff Eqns Appl，2014，20:49－57．

［15］YAMAMOTO K．On the weaker forms of the specification property and their applications［J］．Proc Am Math Soc，2009，137(1):3807－3814．

［16］朱道宇．一类三维分段线性系统的异宿轨的存在性［J］．四川师范大学学报(自然科学版)，2016，39(3):377－381．

［17］陈永胜，范钦杰．不等长代换系统的混沌性态的研究［J］．四川师范大学学报(自然科学版)，2008，31(6):670－673．

［18］GROSSE－ERDMANN K G，PERIS A．Linear Chaos［M］．London:Springer－Verlag，2011．

The Strong Specification Property of Backward Shift Operator on Frechet Sp ace

ZHOU Guangya

(Sichuan Engineering Technical College，Deyang 618000，Sichuan)

This note characterizes the strong specification property of the backward shift operator defined in Frechet space with an unconditional basis in terms of Devaney chaos，and generalizes the main results obtained in(S．Bartoll S，F．Martinez－Gimenez，A．Peris．J Diff Eqns Appl，2012，18:599－605．)to Frechet space．

specification property;Devaney chaos;backward shift;Frechet space

O189．1

A

1001－8395(2016)05－0678－04

10．3969/j．issn．1001－8395．2016．05．011

(编辑 郑月蓉)

2016－04－16

国家自然科学基金(11501391)

周光亚(1957—)，男，副教授，主要从事动力系统的研究，E－mail:zhouguangya1957@163．com

2010 MSC:47A16;47D06;54H20;47B37