面板数据模型下的出租车资源配置合理性研究
——基于“滴滴打车”软件的数据
2016-06-05肖蓬福州外语外贸学院福建福州350202
肖蓬(福州外语外贸学院福建福州350202)
面板数据模型下的出租车资源配置合理性研究
——基于“滴滴打车”软件的数据
肖蓬(福州外语外贸学院福建福州350202)
即使在“互联网+”时代,“打车难”现象仍一直受到政府和社会各界的高度关注。用面板数据(Panel Data)与空间自回归(Spatial Autoregressive)相结合的时空数据自回归模型,通过java程序挖掘相关数据,对互联网时代出租车资源问题进行分析,结果表明:不同时间、区域的出租车资源配置存在显著差异。
面板数据模型;向量自回归模型
移动打车软件,如“滴滴”打车,作为一种创新的商务模型,从乘客与出租车司机之间信息不对称入手,缓解了乘客“打车难”与出租车司机“空载率”居高不下的问题。目前学术界在打车软件领域的研究甚[1-5]少,本文打车软件的视角出发,试图通过建立相关指标,探索出租车资源的“供求匹配”程度的时空差异。
1.数据来源
目前,打车软件市场中“滴滴打车”和“快的打车”软件占有率达99%,且二者已于2015年合并,本文基于“滴滴快的智能出行平台”(http://v.kuaidadi.com/)的数据,利用Java程序(详见附录1)挖掘数据。主要采用北京、成都、广州、杭州、南京、上海、深圳、沈阳、武汉、西安这十大城市的在一周内每小时的数据,主要提取X1(出租车需求量)、X2(被抢单时间)、X3(出租车分布)和X4(车费)及Y(打车难易度)的数据进行处理,挖掘的数据十个城市共1680个数据。
2.从相关系数角度看打车难易程度和各因素的协调关系
利用挖掘的数据十个城市共1680个数据,对X1、X2、X3、X4、Y5个变量用SPSS软件进行标准化处理.在Pearson检验下,Y(打车难易度)与X1(出租车需求量)、X2(被抢单时间)、X3(出租车分布)和X4(车费)对之间的相关性在0.05水平上显著相关。
3.向量自回归模型(VAR)及Panal Data模型原理及实证分析
3.1 研究方法
3.1.1 向量自回归模型
向量自回归模型(Vector Auto-regression,VAR)的建立对研究多变量时序的变动关系有重要意义。向量自回归(VAR)模型的构造思路是把所有内生变量的滞后项作为解释变量,同时,把单变量模型推广到多元,组成了“向量”自回归模型。VAR模型的重点在于通过探索随机扰动对于系统的冲击,并分析结果,进而对系统冲击带来的影响进行解释和预测。VAR模型的形式如:
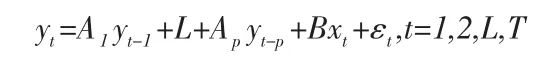
其中:yt是k维内生变量,xt是d维外生变量,p是滞后阶数,T是样本个数。A1,...,Ap,B都是所要估计的系数矩阵。εt是k维扰动向量。
3.1.2 Panal Data模型原理
设有因变量yit与k×1维解释变量向量xit=(x1,it,x2,it,...,xk,it)'满足线性关系。
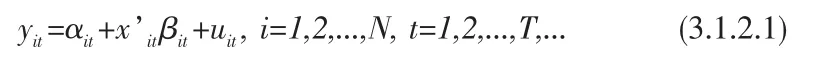
式子(3.1.2.1)是考虑因变量与k个解释变量、N个截面成员及T个时间点上的变化关系。N为截面成员的个数,T为每个截面成员的观测时期总数,参数αit为常数项,βit是对应于解释变量向量xit的k×1系数向量,k是解释变量个数。设随机误差项uit相互独立,为各个变量的方差,且方差相等。
模型参数的估计可以从以下两点考虑:在时间点上考虑,建立含T个截面成员方程的Panel Data模型;或者从截面成员角度考虑,建立含有N个截面成员方程的Panel Data模型。该模型可简化为:
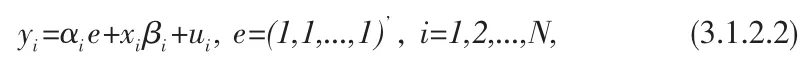
此处αit解释为第i个截面成员的常数项,xi表示第i个截面成员的指标。根据截距向量α和系数向量β中的各分量的不同限制要求,可将Panel Data模型划分为3类特殊的模型:无个体效应影响的不变系数模型、变截距模型、含有个体效应影响的变系数模型。
3.2 实证分析
3.2.1 Granger因果检验
为了保证回归结果的准确性,避免出现伪回归现象,VAR模型要求各变量同阶单整,因此在建立VAR模型之前,有必要对时间序列数据进行平稳性检验。此处,利用A Levin,Lin&Chu t*检验对经过处理后的变量Y,X1,X2,X3,X4进行平稳性检验,由于这些数据都是时序性的,以24小时为变化周期,故对上述5组数据进行一阶差分的单位根检验,检验的结果见表1。

表1 单位根检验结果
从表1可以看出:Y,X1,X2,X3,X4在滞后阶数为24的一阶差分下均通过5%的显著性检验,说明这些变量一阶平稳,可以用于拟合VAR模型。
Granger因果检验结果对滞后长度的p选择极其敏感。滞后阶数太小或太大均会影响模型参数估计的有效性,一般有AIC准则和SC准则比较不同滞后阶数下的统计量,这两个统计量越小,说明模型越有效。通过观察,在滞后阶数p=8时,各个统计量通过显著性检验。故选择滞后阶数为8。确定滞后阶数后,表2给出Granger因果检验结果:

表2 Granger因果检验的结果
从表2的结果可以看到,在10%的显著性水平下,X1(出租车需求量)和Y(打车难易度)互为Granger原因,说明二者之间是互相反映的;在第二组检验中,在10%显著性水平下,拒绝原假设X2(被抢单时间)不能一起Y(打车难易度),数据表明X2、Y互为Granger原因,二者之间是互相作用的;在第三组假设检验中,在10%的显著性水平下,拒绝原假设X3(出租车分布)不能granger引起Y(打车难易度),即出租车分布情况能解释打车难易度,而由于Y不能Granger引起X3的概率为43.83%,所以不能拒绝原假设,说明打车难易度不能解释车辆分布数量。同理,在第四组假设检验中,X4(车费)在10%的显著性水平下拒绝原假设,说明车费收入多少对打车难易度具有显著的Granger影响,但反之不成立。
Granger因果检验说明了指标X1、X2、X3、X4、的波动都能够合理反映于Y。用这四个指标说明对Y建立模型,可避免伪回归产生。
3.2.2 Panel Data模型
首先,利用计算机程序提取数据,全国10个重要城市关于打车难易度、出租车需求量、被抢单时间、出租车分布及车费的168个时间点的数据,利用Eviews软件创建Pool并运行,得到全国10个重要城市的打车难易度的个体效应模型。考虑空间特定效应的变截距模型,即让变截距的模型中的截距项作为时间恒量(截距项不随时点变化),仅随空间单元变化,我们得到了表3,不难发现时空特定效应模型的拟合优度为0.8875说明时间效应对“打车难易度”的影响很大。同时发现,空间差异对打车难易度的影响则比较明显。引入时空特定效应模型以后,R2从0.6325增至0.8875。如此高的拟合优度完全是对各截面各单元的特定效应的肯定,反映了全国10个市的打车难易度的值存在时空差异性。

表3 变截距时空模型的拟合优度
其中反映各地区打车难易度对平均打车难易度的偏离(α*)的估计结果由表4给出。

表4 各地区打车难易度对平均打车难易度偏离(α*)的估计结果
这结论说明,一线城市的出租车打车不一定就难,如上海目前的出租车供给能力“自我消化”城市打车难问题,但与此相反,北京作为一线城市,其交通网却很拥堵,而且经常出现打车难线性,这一点在苍穹数据库中也能体现。

图1 一周内不同时间段对平均打车难易度(γ*t)的偏差值
4.结论与讨论
通结合Panel Data模型的基本思想,建立时间特定效应回归模型、空间特定效应回归模型及时空特定效应回归模型,根据拟合优度得知出租车资源配置存在显著的时空差异特征,且杭州、上海打车相对容易,而“打车难”现象频繁在北京、广州、沈阳、西安、南京出现。同时,07:00-09:00、13:00-14:00及17:00-20:00时间段是到打车高峰期,且每周五、周六、周天均为打车难的日期。
[1]包希璐.南京滴滴打车满意度研究——基于顾客感知价值[J].管理观察,2015 (18).
[2]李骏.快的+滴滴:引领移动互联网成功营销的启示[J].传媒评论,2015(03).
[3]李冬新,栾洁.滴滴打车的营销策略与发展对策研究[J].青岛科技大学学报(社会科学版),2015(01).
[4]李林,陈吉慧.我国移动支付商业模式发展趋势研究[J].商业时代,2010 (30).
[5]陈芬.打车软件撬动了什么[J].中国经济信息,2014(11).
TP319
A
2095-7327(2016)-12-0155-02
基金来源于福州市社会科学研究规划课题(课题批号为2015C03)。
肖蓬(1954.11—),男,副教授,研究方向为应用数学。
