基于离散萤火虫算法的近红外波长优选方法研究
2016-06-05刘泽蒙张广明陈可泉
刘泽蒙、张 瑞、张广明*、陈可泉*
1. 南京工业大学电气工程与控制科学学院、江苏 南京 211816 2. 南京工业大学生物与制药工程学院、江苏 南京 211816
基于离散萤火虫算法的近红外波长优选方法研究
刘泽蒙1、张 瑞2、张广明1*、陈可泉2*
1. 南京工业大学电气工程与控制科学学院、江苏 南京 211816 2. 南京工业大学生物与制药工程学院、江苏 南京 211816
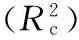
离散萤火虫算法; 近红外光谱; 波长选择; 丁二酸发酵
引 言
近红外光谱技术具有快速、方便、低成本以及无损的特点、广泛应用于医药、农业、石油化工、生物工程等多个领域[1-2]。在采用样本近红外光谱数据进行校正模型建立的过程中、为了降低模型的复杂度、提高校正模型稳健性以及增强模型预测能力、需要对光谱数据进行优化筛选。数据筛选的方法主要有相关系数法、连续投影法、无信息变量消除法、蒙特卡洛法、间隔偏最小二乘法等。近年来广泛应用的群智能优化算法也广泛应用于波长优选、如:遗传算法、粒子群算法和蚁群算法等[3-4]。群智能优化算法强大的全局搜索能力、使得它们在特征变量筛选方面具有巨大的潜力。
剑桥大学的Yang教授在2008年提出了萤火虫算法(firefly algorithm)[5]、萤火虫算法属于群智能优化算法、在连续域的应用十分广泛。其离散形式的萤火虫算法在一些应用中也优于现有算法如蚁群算法、粒子群算法[6]等、并多应用于图像分割、调度和旅行商问题[7-9]等,国内也有将其改进之后应用于其他领域、马建华等将算法引入自由曲面测量序列规则的研究[10]、曾冰等将其应用于装配序列规划研究中[11]、都取得了较好的结果。但在近红外光谱处理领域还未有应用、本实验通过测量丁二酸发酵过程中发酵液的吸光度光谱、将FA方法进行修改后应用于光谱波长变量的筛选、优选后的波长变量由PLS建立校正模型。现今、多采用GA遗传算法作为光谱变量筛选方法[12]、所以在最后不仅与全光谱、还与标准GA-PLS波长优选方法进行比较、证明了该方法能够较好地处理波长变量优选问题。
1 实验部分
1.1 萤火虫算法
1.1.1 标准萤火虫算法
在应用萤火虫算法时需要作出三个假设[5]:
(1) 所有的萤火虫没有性别之分。
(2) 吸引度与亮度成正比。亮度越大说明吸引度越大,即亮度低的个体向更高的个体移动。个体的相对位置和光照吸收率可以影响吸引度大小。
(3) 当萤火虫个体是可见范围内最亮的时,该萤火虫将在空间内随机移动。
在标准萤火虫算法中、分别定义了距离、亮度(吸引力)和移动规则等参数。其数学描述如下:
在萤火虫算法中、萤火虫p对萤火虫q之间的距离定义如下
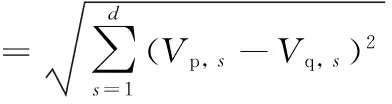
(1)
式(1)中、d为个体萤火虫的坐标维数、Vp,s和Vq,s分别是空间坐标Vp和Vq的第s维分量。
萤火虫p对萤火虫q吸引度β定义如下
(2)
式(2)中、β0为萤火虫之间的距离为0时的吸引力、光照吸收率γ为待定参数。
当萤火虫p受到萤火虫q吸引力较大时、萤火虫p的移动规则如下
(3)
式(3)中、步长系数a为待定参数、rand为0到1之间的随机数。
1.1.2 离散化FA算法
标准萤火虫算法的解空间是连续的实数域、为了将FA算法应用于近红外光谱的特征提取、FA算法需要进行离散化处理以及适合于波长选择的修改。
首先要对萤火虫的位置进行重新编码、由于近红外光谱波长变量数较大、且相邻波长之间的特性相似、将波长变量分为若干个区间、从而进行区间的选择、采用二进制编码0/1分别代表选中的区间以及未被选中的区间。
个体萤火虫形式为:
Ii=[ii,1,ii,2,…、ii,n]Ii,n为波长点
其距离公式则变为如下形式
rpq=Ip-Iq
(4)
由式(2)可看出、吸引度β只随着距离的增大而变弱、而与萤火虫的绝对亮度(目标函数值)无关、与实际情况不符、式(2)中的β0可采用公式(5)计算
(5)
即计算两个萤火虫亮度之差并进行归一化处理。将式(5)带入式(2)可得到两只萤火虫之间的亮度与距离关系、当距离不变相对亮度变大、相应的吸引力也会变强、反之变弱; 当相对亮度不变距离变大、吸引力下降、反之变强。
在大种群中、萤火虫个体分布稀疏时、难以找到具有强吸引力的萤火虫、只能随机振荡。通过增加种群最优值对群体中的其他个体提供牵引作用、提高种群中个体萤火虫的信息往来。将移动公式修改为如式(6)[13]
(6)
其中、式ωrand(Ibest-Ip)体现了当前种群最优个体对其他萤火虫个体的影响力、ω为牵引权重、该式不仅能够使种群之间在迭代初期保持较强的信息沟通能力、还可以促进萤火虫种群移动的多样性、增加可行解的搜索范围、大大提高寻找全局优化解的可能性。同时、将种群最优萤火虫替换最差萤火虫、即采用精英保留策略、加快收敛速度。
文献[14]报道以阈值为分界点、通过比较阈值、决定其是0或1。本研究中采用了文献中计算阈值的改进方法、为了使阈值落于[0,1]、使用映射式(7)
(7)
在采用以上策略离散化后、通过结合标准萤火虫算法流程与离散化参数的数学描述、得到离散萤火虫算法。在近红外光谱波长优选中、选用校正模型的性能指标之一的交叉验证均方根误差作为目标函数、其公式为
(8)
Yi为真实值、Yv为预测值、n为校正集样本数; 将RMSECV作为离散萤火虫算法的目标函数、得到算法流程伪代码。
初始化种群:Ii
算法参数的设定:光照吸收率γ、步长参数α、牵引权重ω
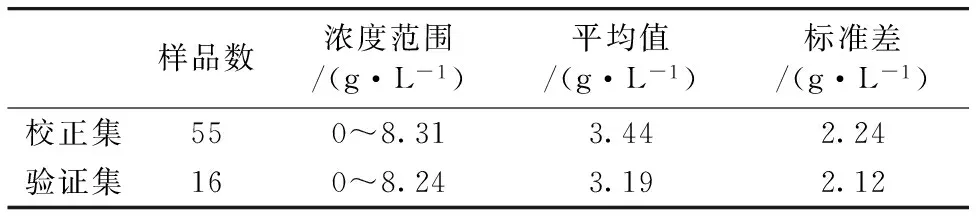
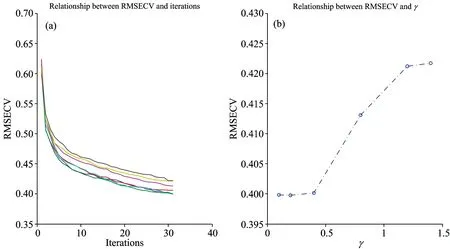
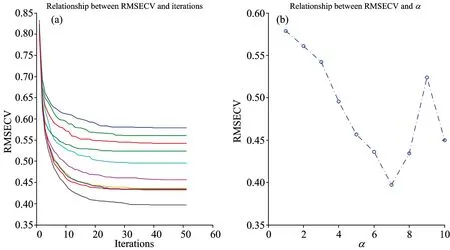
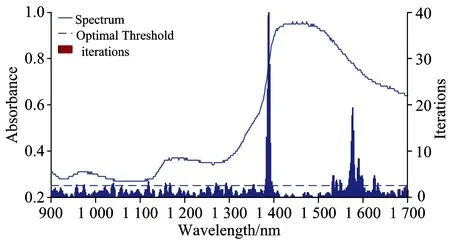
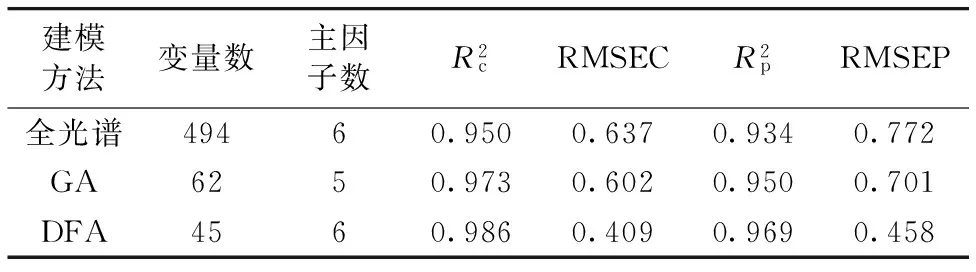
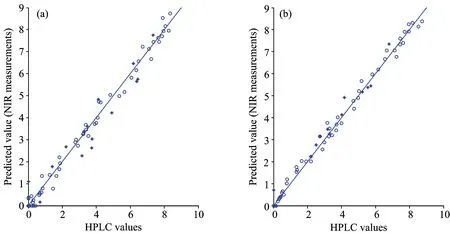
While(t For i=1: n For j=1: n If(RMSECVj>RMSECVi) If(f(Ij’)>rand(1)) Ij= Ii If(RMSECVi>RMSECVj) If(f(Ii’)>rand(1)) Ii= Ij Endfor j Endfor i 更新RMSECV值、标记最亮萤火虫位置 Endwhile 2.1 NIR光谱的采集 光谱采集装置采用Sol1.7型号的近红外光纤光谱仪(BWTek公司)、光谱测量所用光源为恒流卤钨灯、所测样本为实验室中5L发酵罐中的丁二酸发酵液、每30 min取一次、共取78个样本、样品经离心取上清液。采用光程为10 mm的光纤探头进行检测、在常温、恒定pH 6.8条件下进行近红外光谱的测量、光谱采集扫描32次、取平均值代表该样品光谱、分辨率为4 nm、扫描范围900~1 700 nm。本实验光谱数据的采集使用光谱仪自带采集软件BWSpec4、数据的预处理与相关算法的实现均采用Matlab软件实现、78个样品的近红外吸光度光谱图如图1所示。 图1 原始近红外光谱 表1 丁二酸浓度的统计学结果 所测发酵液中目标成分丁二酸、利用高效液相色谱方法(HLPC)测其含量[15]、其化学值统计如表1所示。 采用蒙特卡罗法剔除了奇异样本6个、剩下的样本将运用K-S方法将样本集分为校正集55以及验证集16。 2.2 DFA变量筛选 2.2.1 调节参数 在DFA中、除了种群大小P对DFA算法的迭代效率有所影响外、需要调节算法中的光照吸收率γ、步长系数α、牵引权重ω。默认对DFA算法进行多次运算、取适应度函数最优值作为结果、并取其平均值作为参数调整过程的评判标准。 P以10为间隔、取值范围从20~80、当P值增加、提高了种群的多样性、经多次迭代尝试后、当P取值在40以上、寻优精度并无提高、无需再增加种群规模、体现了萤火虫算法的并行特性。 γ以0.2的间隔取值为[0.1,1.6]; 其他参数默认不变的情况下、γ变化与适应度函数值的关系如图2(a)所示。 图2 RMSECV随γ参数变化的趋势图 图3 RMSECV随α参数变化的趋势图 由图2(b)可看出、随着γ变大、RMSECV收敛渐缓、当其值在0.1~0.4时最终RMSECV趋于平稳、当超过0.4后、最小RMSECV值逐渐增大、即校正模型的性能逐渐变差。 适应度函数值随着α的变化而受到影响、变化情况如图3所示。 α的取值范围为[1,10]、间隔为1。由图3(b)可知、当α增至7时、最小RMSECV达到最佳、随后校正模型变差、由于图3(a)中RMSECV采用的是多次计算取平均、8之后的取值在迭代过程中、其终止结果变化范围较大、说明优选结果极易陷入局部最优。 牵引权重ω表示每次种群迭代中最优萤火虫所占权重、在牵引权重公式中加入衰减系数Δ、迭代初始期需要接近于1的ω、以增强种群中各萤火虫的联系、快速收敛至全局最优、而随着ω的逐渐变小、在迭代后期、逐渐脱离消除当前最优萤火虫的影响、以免陷入局部最优。 由以上可知、DFA算法的参数设定如表2所示。 表2 DFA的相关参数设置 2.3.2 变量选择 参数设定后、采用DFA算法对光谱数据进行筛选、经算法处理后、如图3所示、根据波长变量频率由高到低进行选择、图3中虚线表示所选变量频率次数最低值、当某段区域的迭代次数低于该阈值时、即表示忽略该区域; 反之、选择该区域。而阈值从50开始递减、步长为2、随着噪音和不相关区域的去除、模型性能指标趋于稳健和精准、而阈值继续减小会去除含有有效信息的区域、以此判断并确定阈值大小。 由图4可知、其选择的区域主要在1 370~1 420、1 550~1 560和1 570~1 610 nm等波段、而丁二酸中甲基基团吸收峰多集中于1 100~1 200、1 350~1 400和1 650~1 700 nm区域、次甲基吸收峰多集中于1 150~1 200、1 400~1 450和1 650~1 700 nm区域、其羧基官能团在1 900 nm处吸收峰明显、可看出所选择的主要区域与理论有机基团吸收峰区域大多有所重叠、同时DFA选择了少量相关性较强的吸收谱带、以增加建立模型所需的信息量。 图4 波长变量的选择分布 2.4 建立校正模型 表3 丁二酸浓度的各定量校正模型性能比较 图5 校正模型回归 由表3可知、两种波长变量筛选方法均能很好的提高校正模型的预测精度、但DFA效果要优于标准GA优化算法以及全光谱建模、变量数由494降至45、变量数要少于GA优化方法所筛选的变量数、且模型的相关系数以及RMSECV也要优于以上两种方法、可看出在波长选择阶段、FA算法不仅尽可能的剔除了噪声数据、而且保存了较稳定的波段用于校正模型的建立。基于DFA波长优选建立的模型回归效果如图5所示。 基于发酵过程中发酵液丁二酸含量建立近红外光谱PLS校正模型、对近红外光谱进行波长优选、实验结果显示DFA波长优选建立的PLS校正模型优于全光谱、GA优化算法; 提高了模型建立的效率、增强了模型的精确性和稳定性。本文只针对近红外光谱波段优选的应用进行了部分修改、还可与其他传统波长优选方法进行混合应用或利用优化算法进行DFA的参数调节、继而提高算法的普适性和外推能力。说明了DFA以及其所代表的群智能算法在近红外光谱分析领域具有巨大潜力与实用价值。 该算法也有其不足之处、如参数调节对其收敛性影响较大、理论基础薄弱等。萤火虫算法在近红外分析领域的理论和应用两方面都有重要意义。 [1] CHU Xiao-li、YUAN Hong-fu(褚小立、袁洪福). Modern Instruments(现代仪器),2011、17(5): 1. [2] KONG Cui-ping、CHU Xiao-li、DU Ze-xue,et al(孔翠萍、褚小立、杜泽学、等). Chinese Journal of Analytical Chemistry(分析化学),2010、38(6): 805. [3] XIA A-lin、YE Hua-jun、ZHOU Xin-qi,et al(夏阿林、叶华俊、周新奇、等). Chinese Journal of Analysis Laboratory(分析试验室),2010,29(9): 18. [4] GUO Zhi-ming、HUANG Wen-qian、PENG Yan-kun,et al(郭志明、黄文倩、彭彦昆、等). Chinese Journal of Analytical Chemistry(分析化学),2014,42(4): 513. [5] Yang Xinshe. Firefly Algorithms for Multimodal Optimization. International Symposium on Stochastic Algorithms SAGA 2009: Stochastic Algorithms: Foundations and Applications,2009. 169. [6] Zouache D,Nouioua F,Moussaoui A. Soft Computing,2016,20(7): 1. [7] Rodrigues P S,Wachs-Lopes G A,Erdmann H R,et al. Pattern Analysis and Applications,2015,18(2): 1. [8] Karthikeyan S,Asokan P,Nickolas S. The International Journal of Advanced Manufacturing Technology,2014,72(9-12): 1567. [9] Jati G K,Suyanto. Evolutionary Discrete Firefly Algorithm for Travelling Salesman Problem. in: Adaptive and Intelligent Systems,Springer-Verlag Berlin Heidelberg,2011. 393. [10] LI Ming-fu、MA Jian-hua、ZHANG Yu-yan,et al(李明富、马建华、张玉彦、等). Computer Integrated Manufacturing System(计算机集成制造系统),2014、33(12): 2719. [11] CENG Bing、LI Ming-fu、ZHANG Yi,et al(曾 冰、李明富、张 翼、等). Journal of Mechanical Engineering(机械工程学报),2013、49(11): 177. [12] CHU Xiao-li、YUAN Hong-fu、LU Wan-zhen(褚小立、袁洪福、陆婉珍). Progress in Chemistry(化学进展),2004、16(4): 528. [13] FU Qiang、TONG Nan、ZHONG Cai-ming,et al(符 强、童 楠、钟才明、等). Computer Science(计算机科学),2014、41(3): 228. [14] Chandrasekaran K,Simon S P,Padhy N P. Information Sciences,2013,249(2): 67. [15] CAI Ting、SU Li、CHEN Ke-quan,et al(蔡 婷、苏 溧、陈可泉、等). Chinese Journal of Bioprocess Engineering(生物加工过程),2007、5(1): 66. Wavelength Variable Selection Method in Near Infrared Spectroscopy Based on Discrete Firefly Algorithm LIU Ze-meng1,ZHANG Rui2,ZHANG Guang-ming1*,CHEN Ke-quan2* 1. College of Electrical Engineering and Control Science,Nanjing Tech University、Nanjing 211816,China 2. College of Biotechnology and Pharmaceutical Engineering,Nanjing Tech University、Nanjing 211816,China Discrete firefly algorithm; Near infrared spectroscopy; Wavelength variable selection; Succinic acid fermentation Aug. 27,2015; accepted Dec. 9,2015) 2015-08-27、 2015-12-09 国家(863计划)项目(2015AA021005)、江苏省产学研联合创新基金项目(BY2014005-07)资助 刘泽蒙、1990年生、南京工业大学电气工程与控制科学学院硕士研究生 e-mail:wfwgghb@njtech.edu.cn *通讯联系人 e-mail:kqchen@njtech.edu.cn; zgmchina@163.com O657.3 A 10.3964/j.issn.1000-0593(2016)12-3931-06 *Corresponding authors2 结果与讨论

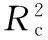
3 结 论