核优化相关向量机太赫兹频谱特征提取方法

钟毅伟、沈 韬,2*、毛存礼、余正涛

1. 昆明理工大学信息工程与自动化学院、云南 昆明 650500 2. 昆明理工大学材料科学与工程学院、云南 昆明 650500

核优化相关向量机太赫兹频谱特征提取方法

钟毅伟1、沈 韬1,2*、毛存礼1、余正涛1

1. 昆明理工大学信息工程与自动化学院、云南 昆明 650500 2. 昆明理工大学材料科学与工程学院、云南 昆明 650500

太赫兹频谱对分子非局域振动模式的变化较为敏感。因此、其波形容易受到多种理化因素的影响、会产生峰值改变、频移、甚至整体波形的变化、单一地从固定峰值特征与物质的对应关系上进行组分分析和物质鉴别容易产生较大误差甚至错误。针对此问题、提出区别于局部特征提取方法的基于核优化相关向量机(KO-RVM)的整体图形特征提取方法、并与支持向量回归算法(SVR)进行比较。结果表明、经过期望最大化算法进行基函数参数控制的RVM适用于太赫兹透射谱的特征提取、可对每种物质的光谱数据进行稀疏表示、控制提取图形特征的数量。利用已提取特征构造的模型能够还原频谱曲线的整体特征、对谱线各频段的拟合效果更加一致、同时所提取的特征还可作为不同物质间太赫兹光谱相似性度量和共同特征发现的依据。

太赫兹频谱； 特征提取； 相关向量机； 核函数优化

引 言

多数大分子物质的转动及部分振动能级位于太赫兹波段、如非局域的分子内振动、骨架振动、氢键、范德华力等。此类振动易受外界物理和化学环境变化的影响、使其太赫兹频谱波形发生不同程度的改变[1-2]。如文献[3-6]中牛血清蛋白、青霉胺同质异构体、双氯芬酸和四烷基铵盐的实验中、在温度变化、分子结构改变、水分蒸发、分子大小及颗粒形状不同、或共晶体形式转变时、太赫兹频域透射谱都会发生不同程度的整体变化、同时发生峰值改变和频移。此类研究说明、在不同实验条件下、相同物质的太赫兹频谱测量结果会有很大区别、多数共晶体和有机大分子无法通过标定少数峰值特征进行定性分析。而传统的分析方法目前仅可对一些理想条件下的化合物、共晶体以及同质异构体标定明显的吸收峰。如文献[7-9]中就对蔗糖结晶、微晶纤维素、尿嘧啶-尿素共晶体等物质的特征吸收峰进行了标定、并利用其吸收峰进行结晶度和混合物浓度等方面的估计。从中我们可以看出、传统方法在对太赫兹频谱特征进行分析时、多次进行特征峰值出现位置或固定采样点处频谱参数的判断、同时结合数学模型的推导。如Partha等利用TCF(时间相关函数)结合高斯衰减模型及涨落耗散定理、拟合多种烷烃溶剂中硝基苯的太赫兹频谱[10]。整个分析过程将会极大地增加模型复杂度和计算成本、对于计算机性能和分析人员的专业知识提出了极高的要求。而且、研究人员目前尚未发现太赫兹频谱的各类图形特征(如峰高、峰宽、峰值频率和波形整体斜率等)与对应物质的理化性质之间的确切联系。在此情况下、研究快速有效的物质太赫兹频谱整体图形特征提取和分析方法、去除冗余信息的同时保留主要图形特征、可为物质分类、理化性质与频谱图形的对应关系研究起到良好的支撑作用。

除了在传统方法中结合德拜模型、比尔-朗伯定理等数学模型进行分析外、目前广泛应用的太赫兹频谱特征分析方法有主成分分析法(PCA)、支持向量机(SVM)、支持向量回归(SVR)、偏最小二乘法(PLS)等[11-15]。其中PCA和PLS方法对频谱的特征提取过程为多个采样点组合的线性映射、所提取的特征维没有与原频谱的图形对应关系或物理对应关系、但是得到的特征具有较高的有效性和区分度、可用于物质分类和聚类分析。PLS在文献[15]中的各改进算法可分区间进行PLS拟合、并选取拟合精度最高的频率区间作为特征谱区构造定量回归模型。但是这种应用方法所提取的特征为局部特征、不利于表达频谱波形的整体特征。而利用PLS或SVM进行拟合时、提取特征的数量难以控制、不利于频谱全谱的稀疏表示以及后续的特征向量构造。针对此问题、本文拟用期望最大化算法对训练数据集上的RVM核函数参数进行寻优、同时提取太赫兹频谱的整体图形特征、控制特征提取的数量、以期用稀疏的特征点和平滑的拟合模型最大程度地保存频谱的主要峰值频率、峰高、峰宽和波形整体斜率等全局图形特征。并利用重构的拟合模型与3种滤波后的频谱曲线进行比较、以检验其拟合模型的特征保存程度、再与SVM的改进算法进行比较。

1 数据预处理

受实验仪器本身的信号干扰和环境波动的影响、样品的太赫兹光谱中通常会带有少量噪声、且此类噪声往往由多个元误差因素叠加产生。此类情况符合大数定律中高斯分布的假设、因此我们采用S-G滤波和两种小波变换对原频谱数据进行滤波、去除其中的高斯噪声和其他高频噪声、得到3种滤波后的频谱数据。本文所采用的数据为抗坏血酸(ascorbic acid)在0.9～6 THz、温度300 K、PE基质中含量为5%的条件下的透射谱、并四苯(tetracene)在0.9～6 THz、温度60 K、PE基质中含量为5%条件下的透射谱、以及核黄素(riboflavin)在0.9～6 THz、温度300 K、PE基质中含量为10%条件下的透射谱。

在以上的数据基础上、我们使用核优化RVM算法(kernel optimized RVM)对未经滤波的数据进行特征提取、并利用所提取的特征进行回归模型重构。分别使用启发式阈值小波消噪、固定式阈值小波消噪和Savitzky-Golay滤波算法对原数据进行处理、并计算回归模型与这3种滤波数据的均方根误差MSE、以直观地对比重构模型所保存特征的有效性。

2 RVM回归模型

特征提取是对信号的测量指标进行整合、重组和取舍的过程、其目的是去除冗余、噪声、并将信号转化为利于后续处理的表达方式。对于光谱而言、直接提取原曲线中的关键图形特征点更有利于理化性质与图形特征对应关系的分析、也将有利于物质频谱分类和相似性度量方面的研究。相关向量机是由Michael E Tipping于2001年提出的一种基于稀疏贝叶斯框架的有监督回归训练模型[16]。此方法在支持向量机的结构风险最小化理论和由权重决定的超曲面分类模型基础上、提出为每个权重分配一个先验正态分布、通过优化这些先验分布中各参数自身的分布、使多数对构造回归模型或分类模型影响微小的基函数所对应的权值由于先验分布p(wi|α)以及p(wi|t，α，σ2)快速收敛于0而被修剪(α和σ2即为分布超参数)。相关权值及其对应的相关向量被训练出来、利用相关权值与基函数矩阵的乘积构造回归模型或分类模型、以达到稀疏表示的目的。因为相关向量机采用了全概率框架进行参数的迭代优化和训练、避免了传统支持向量机预测结果非概率性、支持向量随训练样本的增长而线性增长、内积核必须满足梅西定理等缺点、进一步增强了泛化能力、提高了预测结果的容错性、并且获得比支持向量机更加稀疏的预测模型。RVM训练得到的权值向量是概率选择的结果而非阈值条件所决定、避免了局部过拟合或欠拟合、更有利于整体图形特征的提取。RVM的学习过程如下：

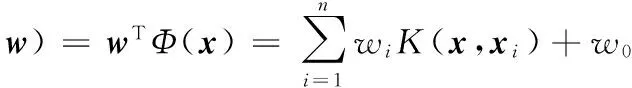
(1)

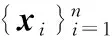
ti=y(xi，w)+εi

(2)

其中εi为噪声项、其均值为零、服从方差为σ2的高斯分布。有了前面的模型和假设、为目标向量分配高斯先验分布、表示为

(3)

通常、我们希望训练得到的权值向量w使上式概率最大、即求出上式的最大似然估计。但是这样会造成所有样本都参与构造模型、得出的权值向量也会导致过拟合问题。在支持向量机理论中、为了避免在不可分模式下的过拟合问题、根据结构风险最小化理论构造权值向量w的最小化泛函、设置了模型复杂度和不可分离点数量之间的平衡参数、以此作为权值向量的约束条件[17-18]。所以在相关向量机的假设中、以类似的思想直接为权值向量的每一个分量添加先验分布以进行约束

(4)

其中、α和β=σ-2为权值向量先验分布函数中的超参数、分别服从Gamma分布、且相互独立、形态参数和尺度参数的初值为0。在定义了权值的先验分布后、需求出未知参数w，α，σ2的后验分布

p(w，α，σ2|t)=p(w|α，σ2，t)p(α，σ2|t)

(5)

式(5)右边第一项为

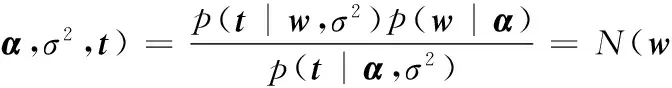
(6)

其中均值矩阵μ=σ-2ΣΦTt、协方差矩阵Σ=(σ-2ΦTΦ+A)-1、超参数对角矩阵A=diag(αi)。因为p(α，σ2|t)正比于p(t|α，σ2)p(α)p(σ2)而α和σ2的先验分布已知、则式(5)右边第二项可通过最大化p(t|α，σ2)而求出

(7)

其中C=σ2I+ΦA-1ΦT。在求解使式(7)概率最大的α和σ2时、无法直接求得它们的解析解(closed form)。因此这里使用的是Tipping等[19]于2003年提出的快速边缘似然最大化方法(fast marginal likelihood maximization)、设超参数向量α的似然函数为

log|C|+tTC-1t]

(8)

将αi对应C的矩阵第i列移除、有

=L(α-1)+l(αi)

(9)

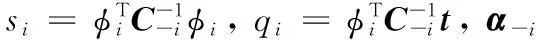
3 基于期望最大化的高斯核函数优化

由于相关向量机的经典框架缺少关于各权值的先验分布中方差之间的结构性先验概率约束、因而其稀疏性仍受核函数及核参数的控制、在一些情况下可能出现低频部分或高频部分欠拟合以及整体波形过拟合或欠拟合的现象[20-21]。为了解决RVM的稀疏性控制问题、近年来许多学者在此课题上提出了一些新的观点。如Schmolck[20]等改造各权值向量的先验分布、即对式(4)进行改进、通过噪声相关平滑函数取代超参数的Gamma分布、从而使权值向量的分布不再服从student-t分布、得到平滑相关向量机(smooth RVM)。但是即使先验足够光滑、该方法也无法保证输出函数的绝对光滑、这也是导致无法适当拟合的原因[22]、而且此方法仍旧依赖于核函数的准确选择和组合、无法通过控制单一参数使算法在所有拟合任务上适用。文献[19]中所阐述的方法对原RVM框架进行了显著的改进、实现了对边缘分布的极大似然函数快速求解、但是在核宽度选择不当的情况下仍不足以提供适当的拟合结果。因此、在能够进行频谱整体图形特征提取的基础上、需进一步降低提取特征的稀疏度、并且各频段的核函数参数的选择应适用于该频段的拟合任务、以获得更加均匀的拟合效果。本文在上述方法的基础上采用了期望最大化核学习方法(exception maximization)、通过分别估计高斯核函数宽度向量的每个分量对L(α)的影响、以解决高斯核函数宽度b2的选择问题[21]。

设输入向量x与原样本集中第i个输入向量xi之间的高斯核函数为

(10)

在原框架中、b=b1=…=bN、核矩阵每一列的核宽度相同、没有根据原信号的频率和噪声特点进行估计。而在最大期望核学习方法中、设核宽度向量为b=[b1、…、bN]、在假设其他参数已知的情况下、求使得式(8)关于向量b最大时的值、并设置核宽度的几何平均为恒定值、作为极大似然优化的约束条件

(11)

(12)

其中μb为核宽度向量均值约束条件。引入拉格朗日乘子λ、则最大似然函数的约束优化问题可表述为

(13)

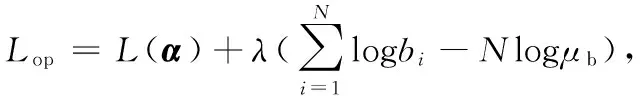
D=(C-1ttTC-1-C-1)ΦA-1=σ2((t-y)μT-ΦΣ)

(14)

其中Dmn=∂L(α)/∂φmn、化简得

(15)

使式(15)为0、并满足均值约束条件、求解各个最优bm、组合得到最优核宽度向量b=[b1、…、bN]。由于在迭代过程中、超参数对角矩阵A不断更新、使得均值矩阵μ及协方差矩阵Σ不断更新、所以L(α)及核矩阵也会相应更新。为避免训练过程出现震荡、核矩阵更新速度设置为低于其他参数更新速度。通过上述迭代训练过程、核优化相关向量机(kernel optimized RVM,KO-RVM)可避免自适应相关向量机(ARVM)和自适应核学习相关向量机(AKL-RVM)采用梯度下降法导致收敛过慢的问题、也可避免sRVM的核函数选择问题、同时计算复杂度没有明显提高、在训练速度上和快速边缘似然最大化方法接近。另外、由于太赫兹频谱波形在不同频段的波动幅度经常出现较大差别、高斯核函数优化的RVM算法可进一步避免不同频段拟合效果不一致的问题、将更加适用于太赫兹频谱的整体图形特征提取以及各频段曲线的拟合。

4 实验及结果分析

4.1 数据

本文所采用的数据为抗坏血酸(Ascorbic Acid)在0.9～6 THz、温度300 K、PE基质中含量为5%的条件下的透射谱、并四苯(Tetracene)在0.9～6 THz、温度60 K、PE基质中含量为5%条件下的透射谱、以及核黄素(Riboflavin)在0.9～6 THz、温度300 K、PE基质中含量为10%条件下的透射谱。以上数据均来源于日本理化研究所太赫兹数据库(www.riken.jp/THzdatabase/)。每组数据采样点数均为6 000以上、保证了光谱曲线的信息量和特征提取时的稀疏度对比、原频率单位波数变换为太赫兹、如图1所示。

4.2 特征提取与重构模型

首先利用epsilon-SVR和KO-RVM对每种物质的透射谱进行特征提取、在两种算法各自的拟合模型与原数据的均方根误差接近时、通过对比支持向量与相关向量的数量差距、来判断在相近的拟合效果下哪种算法所提取的图形特征更稀疏、再进一步对比两种算法根据这些特征所重构出的拟合模型的平滑性。而后、改变epsilon-SVR算法的误差系数以降低其提取特征的稀疏度(即降低支持向量的稀疏度)、对比稀疏度下降的epsilon-SVR模型与KO-RVM模型的拟合效果。

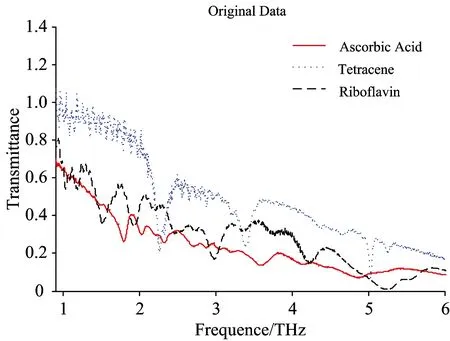
图1 抗坏血酸(Ascorbic Acid)、并四苯(Tetracene)、核黄素(Riboflavin)的太赫兹透射谱曲线

Fig.1 Terahertz transmission spectra of Ascorbic Acid,Tetracene and Riboflavin

由于每种太赫兹光谱检测方法都不可避免地受到多种系统因素和环境因素的共同作用而含有噪声、这类噪声符合大数定律中高斯分布的假设、所以我们应用三种滤除高斯噪声的滤波方法分别得到每种物质的三组透射谱滤波数据、并计算每种算法的拟合模型与滤波数据的RMSE、以此判断训练得到的模型是否保留了光谱的主要特征以及能否拟合原曲线。这里采用的三种滤波方法分别是启发式阈值小波消噪(heursure)、固定式阈值小波消噪(sqtwolog)和Savitzky-Golay滤波(S-G)、如表1所示。

从图2(a)、(d)、(g)可以看到、在保证对三种物质频谱的回归均方根误差(RMSE)均小于3%的情况下、epsilon-SVR的特征稀疏度较低、图中蓝圈表示的支持向量的数量均达到了5 400以上、而我们所采用的频谱曲线样本点数量为6 349、提取特征的数量超过了原样本数量的80%、没有起到很好的特征提取及降维的作用。相对的、核优化RVM对三种物质的拟合误差RMSE均达小于3%、所提取的特征数量占原样本数量的1.5%左右、特征稀疏度较高、可以对原数据模型进行稀疏表示。当调整epsilon-SVR的误差系数和惩罚系数、使其提取的特征下降至4 000以下时、出现了图2(b)、(e)、(h)中较严重的欠拟合现象。此结果说明SVM的改进算法依旧依赖于惩罚系数以及误差系数的设置、在保证拟合效果的情况下无法控制其特征提取的稀疏度。而改进的RVM算法能够在只提取少量关键特征的情况下保证对原光谱曲线的准确拟合、重构模型具有良好的特征还原性、RMSE均小于0.02。

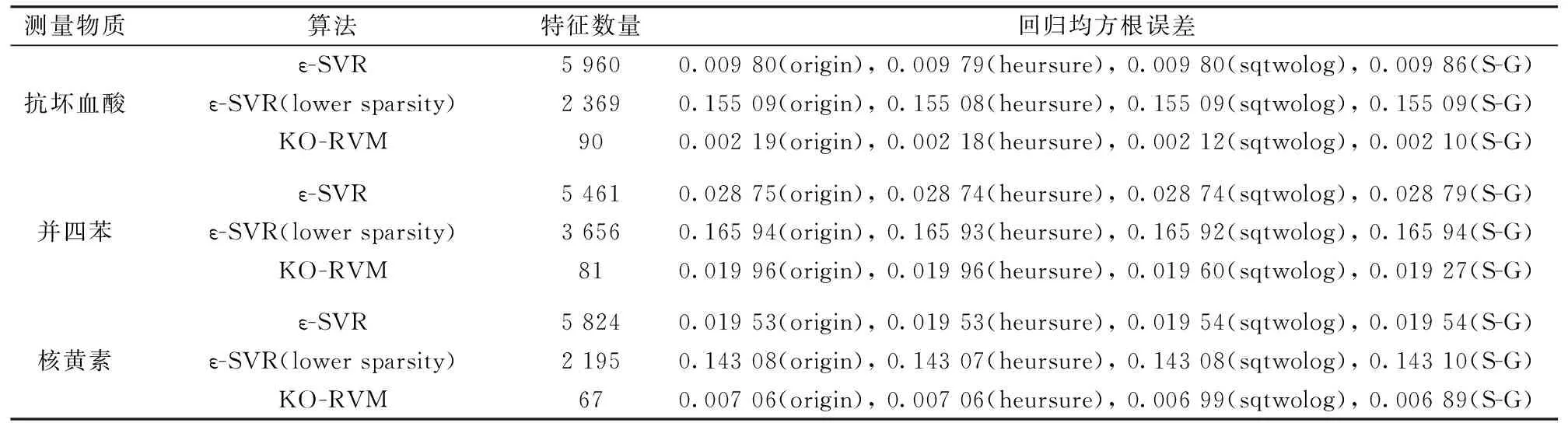
表1 KO-RVM与参数调整后的ε-SVR对比的训练结果及回归均方根误差(RMSE)

另外、从局部放大图2(j)和(k)中可以看到、左边的epsilon-SVR局部拟合模型与原数据误差较大、并且出现了过拟合现象、没有平滑原曲线中的任何毛刺。而核优化RVM算法的拟合模型在平滑了毛刺的基础上、还原了原曲线的主要峰值特征、没有出现频移或剧烈的幅值变化、并且在此基础上提取了少量对重构模型具有关键作用的特征[图2(k)中的蓝圈为提取的图形特征]。相对的、核优化RVM提取的特征较为均匀和稀疏、epsilon-SVR提取的特征集中于震荡剧烈的部分以及峰值附近、且提取的特征数量较多、不利于降低后续分析工作的计算复杂度。

结合图2和表1的实验结果我们可以看出、KO-RVM与参数选择适当的epsilon-SVR拟合效果接近、但是在用于模型重构的图形特征数量上、KO-RVM比epsilon-SVR稀疏两个数量级、且没有降低对原模型的拟合质量。在与3种滤波数据进行对比时、KO-RVM与滤波后数据以及原数据的RMSE均小于0.02、在不刻意进行参数调优的情况下、还原模型未出现过拟合或欠拟合现象、图形特征稀疏性明显。对比拟合模型和原频谱曲线可发现、峰值、峰宽、峰值频率等主要图形特征均未出现明显改变、整体特征保存良好。另外、本实验所采用的SVR和RVM代码在执行效率上不具有可比性、故不作时间复杂度和迭代次数方面的具体分析比较(SVR代码为已编译版本、RVM代码未编译； SVR的平均训练时间为9 s、RVM的平均训练时间为13 s)。

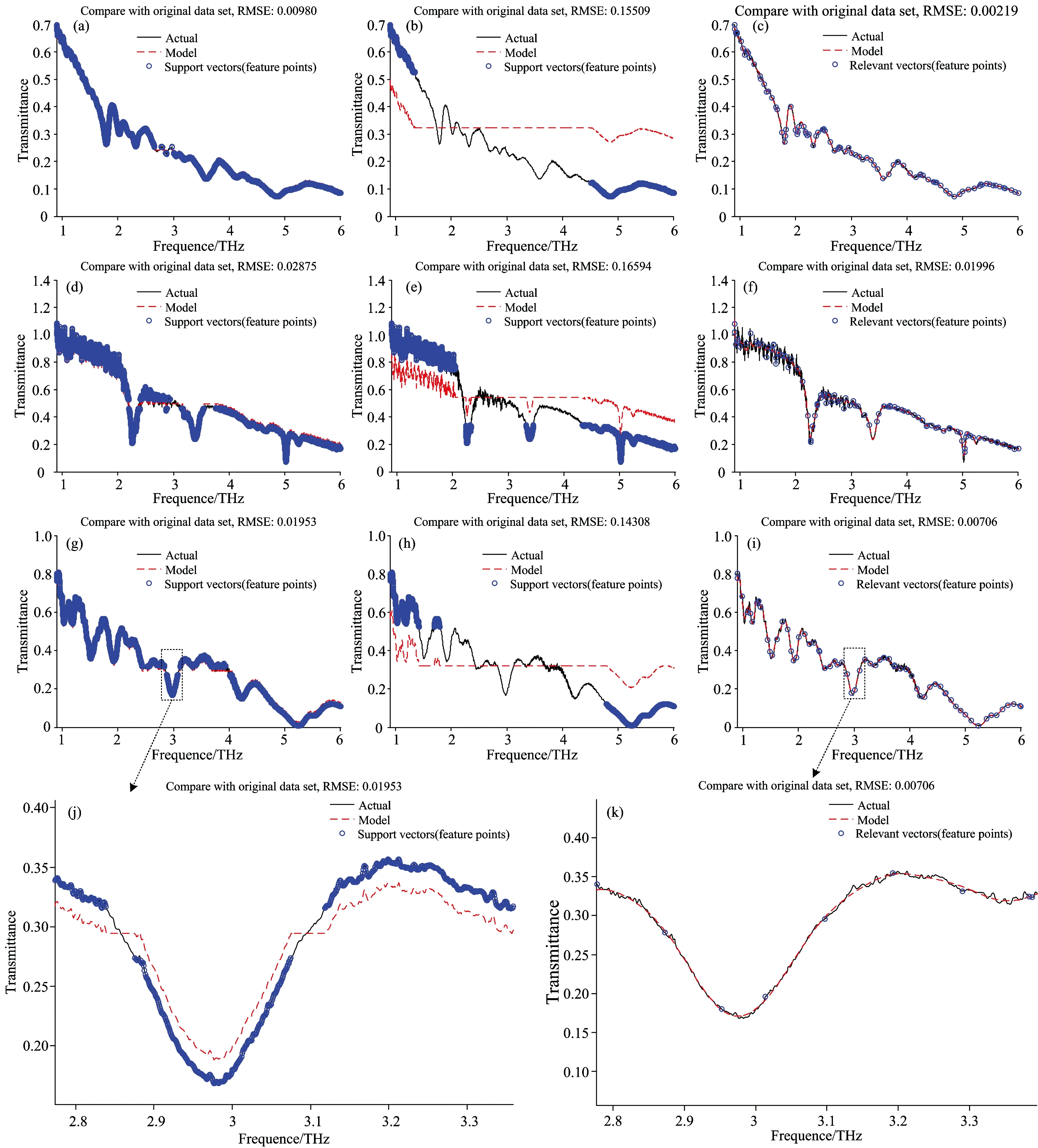
图2 (a)、(b)、(c)为抗坏血酸光谱拟合结果； (d)、(e)、(f)为并四苯光谱拟合结果； (g)、(h)、(i)为核黄酸光谱拟合结果

其中(a)、(d)、(g)为准确拟合的epsilon-SVR算法的拟合模型与支持向量； (b)、(e)、(h)为特征数量降至4 000以下的epsilon-SVR所产生的拟合模型； (c)、(f)、(i)为核参数优化的RVM进行的拟合以及相关向量； (j)、(k)为(g)和(i)的局部放大

Fig.2 (a),(b),(c) showed the fitting results of Ascorbic Acid spectrum,(d),(e),(f) showed the fitting results of Tetracene spectrum； (g),(h),(i) showed the fitting results of Riboflavin spectrum Besides,(a),(d),(g) stand for the good fitting results of epsilon-SVR,and (b),(e),(h) stand for the result of feature sparsity below 4 000； In addition,(c),(f),(i) showed the remarkable fitting result of KO-RVM； Graphs (j) & (k) are the enlarged views of (g) & (i)

5 结 论

在太赫兹频段、化合物、混合物或单质的频域波形受到多种理化因素的影响、会产生峰值变换、频移、甚至整体波形都会产生变化、所以本文在此基础上提出区别于局部特征提取的基于最大期望的核优化RVM整体特征提取方法、并与SVR改进算法进行比较。实验结果表明、在三种有较明显峰值特征以及峰宽较大的有机物光谱的拟合任务中、核优化RVM表现出了优异的拟合精度、拟合模型具有良好的平滑性、与滤波后数据相对比、没有出现明显的过拟合或欠拟合现象。在稀疏度方面、相较于现在应用广泛的用于拟合任务SVM方法、其提取出的用于重构拟合模型的整体图形特征点更加稀疏、在重构拟合模型时更加关键。同时相关向量保留了与原数据图形的物理意义间的对应关系、可为之后的多类物质太赫兹光谱图形的簇内和簇间相似性分析以及成分分析提供便利。以上各项优点都表明了该算法在太赫兹光谱数据量日益丰富背景下、对各类物质的太赫兹光谱与理化性质的图形对应关系的分析研究具有重要意义及应用价值。

[1] Baxter J,Guglietta G. Analytical Chemistry,2011,83：4342.

[2] Fuse N,Takahashi T、Ohki Y,et al. IEEE Electrical Insulation Magazine,2011,27(3): 26.

[3] Ji T,Zhao H,Han P,et al. Nuclear Science and Techniques,2013,24(1): 1.

[4] Burnett A,Kendrick J,Russell C,et al. Analytical Chemistry,2013,85(16): 7926.

[5] Li X,Fu X,Liu J,et al. Journal of Molecular Structure,2013,1049: 441.

[6] King M、Buchanan W、Korter T. Analytical Chemistry,2011,83(10): 3786.

[7] Ueno Y,Rungsawang R,Tomita I,et al. Analytical Chemistry,2006,78(15): 5424.

[8] Kim J,Boenawan R,Ueno Y,et al. Journal of Lightwave Technology,2014,32(20): 3768.

[9] Ermolina I,Darkwah J,Smith G. AAPS Pharmscitech,2014,15(2): 253.

[10] Dutta P,Tominaga K. Journal of Molecular Liquids,2009,147(1-2): 45.

[11] Chen T,Li Zhi,Mo Wei. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy,2013,106: 48.

[12] Ge H,Jiang Y,Xu Z,et al. Optics Express,2014,22(10): 12533.

[13] Avila F,Mora M,Oyarce M,et al. Journal of Food Engineering,2015,162: 9.

[14] El Haddad J,de Miollis F,Sleiman J,et al. Analytical Chemistry,2014,86(10): 4927.

[15] Wang Q,Ma Y. Chemometrics and Intelligent Laboratory Systems,2013,127: 43.

[16] Tipping M. Journal of Machine Learning Research,2001、(1): 211.

[17] Vapnik V. IEEE Transactions on Neural Networks,1999,10(5): 988.

[18] Bowd C,Medeiros F,Zhang Z,et al. Investigative Ophthalmology & Visual Science,2005,46(4): 1322.

[19] Tipping M,Faul A. Fast Marginal Likelihood Maximization for Sparse Bayesian Models. Proceedings of the Ninth International Workshop on Artificial Intelligence and Statistics,2003.

[20] Schmolck A、Everson R. Machine Learning,2007,68(2): 107.

[21] Mohsenzadeh Y、Sheikhzadeh H. IEEE Transactions on Neural Networks and Learning Systems,2015,26(4): 709.

[22] Cheng D,Nguyen M,Gao J,et al. Neural Networks,2013,48: 173.

Terahertz Spectrum Features Extraction Based on Kernel Optimization Relevance Vector Machine

ZHONG Yi-wei1,SHEN Tao1,2*,MAO Cun-li1,YU Zheng-tao1

1. School of Information Engineering and Automation,Kunming University of Science and Technology,Kunming 650500,China 2. School of Materials Science and Engineering,Kunming University of Science and Technology,Kunming 650500,China

Terahertz spectrum is sensitive to the change of the nonlocal molecular vibration mode. Accordingly,the spectral waveform is susceptible to variety of physical and chemical factors,which will lead to peak changes,frequency shifts,and even deformation of the overall waveform. Component analysis and material identification from the correspondence between the fixed peak features and materials will prone to cause errors or mistakes. Therefore,to solve this problem,we proposed a method based on Kernel Optimization Relevance Vector Machine (KO-RVM),which extracts global graphic features to distinct from the local features extraction method. And we use Support Vector Regression (SVR) algorithm as comparison. The result shows that,when basis functions’ parameters of RVM are optimized with expectation-maximization algorithm,it will be suitable for feature extraction of terahertz transmission spectrum. The spectrum can be sparsely represented,and the amount of extracted graphic features is substantially reduced. Reconstruction models based on these features are capable of retaining the overall spectral characteristics,and fitting results for each band are more consistent,while the extracted spectrum features can be used as basis of similarity measurement and the common characteristics investigation between different materials.

Terahertz frequency spectrum; Feature extraction; Relevance vector machine; Kernel optimize

Sep. 4,2015; accepted Jan. 18,2016)

2015-09-04、

2016-01-18

国家自然科学基金项目(61302042),云南省应用基础研究基金项目(2013FD010),昆明理工大学材料学院青年拔尖人才项目(14078343)资助

钟毅伟、1988年生、昆明理工大学信息工程与自动化学院硕士研究生 e-mail: zhongyiweiKM@163.com *通讯联系人 e-mail: shentao@kmust.edu.cn

O657.3

A

10.3964/j.issn.1000-0593(2016)12-3857-06

*Corresponding author