变分代数能量自洽法研究Li2分子部分电子态的解析势能

2016-06-05张春国樊群超孙卫国范志祥

光谱学与光谱分析 2016年12期

关键词：变分势能解析

张春国、樊群超*、孙卫国,、范志祥、张燚

1. 西华大学理学院先进计算研究中心、四川成都 610039 2. 四川大学原子与分子物理研究所、四川成都 610065

变分代数能量自洽法研究Li2分子部分电子态的解析势能

张春国1、樊群超1*、孙卫国1,2、范志祥2、张燚2

1. 西华大学理学院先进计算研究中心、四川成都 610039 2. 四川大学原子与分子物理研究所、四川成都 610065

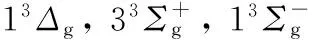
Li2；振动能谱；解析势能函数；变分法；自洽方法

引言

分子精确的振动光谱和解析势能函数是化学物理和原子分子物理领域中重要的研究对象之一[1-3]。获得双核分子精确的振动光谱和解析势能函数不仅可以掌握分子的内部物理行为[4]、还能计算出分子正确的能级结构[5]、从而为原子分子的散射和化学反应碰撞提供有效的数据支撑[6]。此外、精确的双核分子解析势能也是研究多核分子体系解析势能函数与振动能谱的基础[7]。

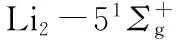
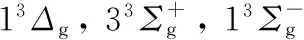
1 理论与方法

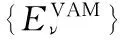
VVAECM(R)=VMHMS(R)+Λ(R)[VMHMS(R)-VM(R)]

(1)

式中VMHMS(R)是对HMS势改进后得到的MHMS势、VM(R)表示的是Morse势、它们分别为

VMHMS(R)=-De(1+a1x+a2x2+a3x3)e-a1x

(2)

VM(R)=De[e-2βx-2e-βx]

(3)

上式中De是分子离解能、x=R-Re、R为分子核间距、Re为分子核间距的平衡位置、β表示为

β=(f2/(2De))1/2

(4)

(5)

势能展开系数an是振动力常数fn的函数[13]

(6)

(7)

(8)

由二阶微扰理论可求出振动力常数fn[13]

(9)

(10)

其中(De,Re,ωe,ωexe,αe)是分子常数、μ是约化质量、式(1)中Λ(R)为变分函数

(11)

通过以下步骤调整式(11)中的变分参数λ来确定解析势能函数的具体形式：

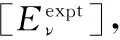
(2)将已知的分子常数(De,Re,μ,ωe,ωexe,αe)利用式(5)、式(9)和式(10)求出振动力常数(f2,f3,f4)、再通过式(6)—式(8)计算展开系数(a1,a2,a3)。

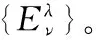
2 结果与讨论

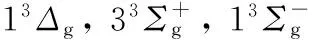
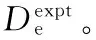
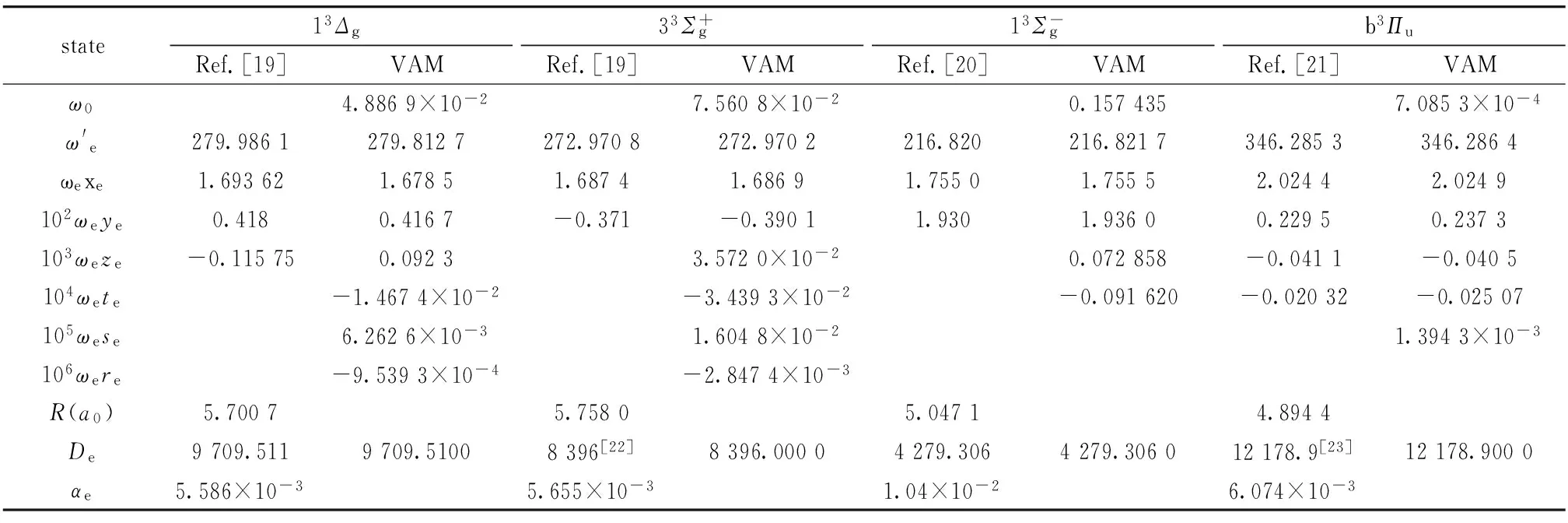
表1 Li2分子部分电子态的分子光谱常数 (cm-1)

表2 Li2分子部分电子态的VAECM势能的力常数fn、展开系数an和变分参数λ

Eh=Hartree=219 474.630 67 cm-1

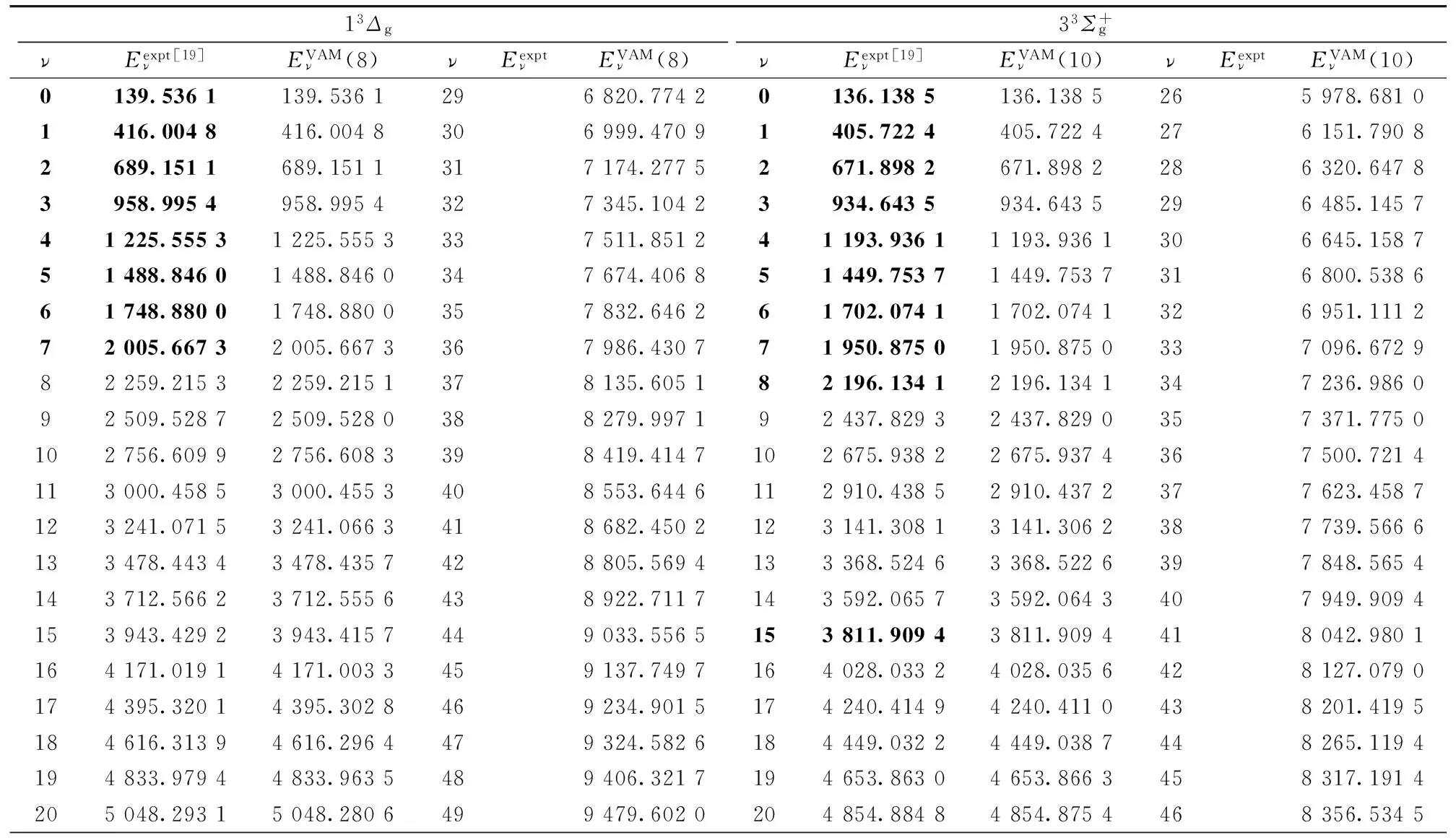
表3 Li2分子部分电子态的振动能级(cm-1)

续表3

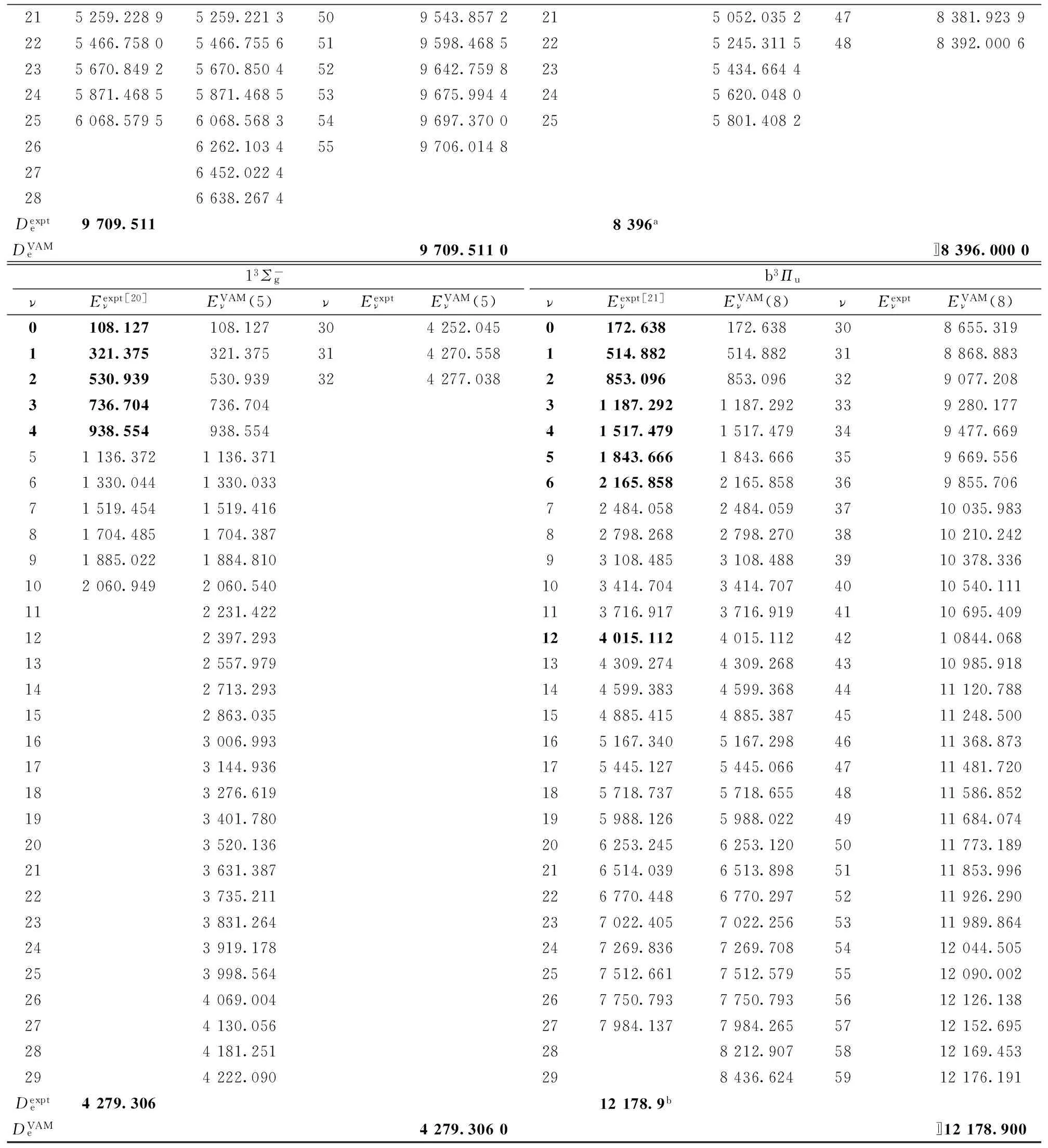
215259.22895259.2213509543.8572215052.0352478381.9239225466.75805466.7556519598.4685225245.3115488392.0006235670.84925670.8504529642.7598235434.6644245871.46855871.4685539675.9944245620.0480256068.57956068.5683549697.3700255801.4082266262.1034559706.0148276452.0224286638.2674Dexpte9709.5118396aDVAMe9709.5110〛8396.000013Σ-gb3ΠuνEexptν[20]EVAMν(5)νEexptνEVAMν(5)νEexptν[21]EVAMν(8)νEexptνEVAMν(8)0108.127108.127304252.0450172.638172.638308655.3191321.375321.375314270.5581514.882514.882318868.8832530.939530.939324277.0382853.096853.096329077.2083736.704736.70431187.2921187.292339280.1774938.554938.55441517.4791517.479349477.66951136.3721136.37151843.6661843.666359669.55661330.0441330.03362165.8582165.858369855.70671519.4541519.41672484.0582484.0593710035.98381704.4851704.38782798.2682798.2703810210.24291885.0221884.81093108.4853108.4883910378.336102060.9492060.540103414.7043414.7074010540.111112231.422113716.9173716.9194110695.409122397.293124015.1124015.1124210844.068132557.979134309.2744309.2684310985.918142713.293144599.3834599.3684411120.788152863.035154885.4154885.3874511248.500163006.993165167.3405167.2984611368.873173144.936175445.1275445.0664711481.720183276.619185718.7375718.6554811586.852193401.780195988.1265988.0224911684.074203520.136206253.2456253.1205011773.189213631.387216514.0396513.8985111853.996223735.211226770.4486770.2975211926.290233831.264237022.4057022.2565311989.864243919.178247269.8367269.7085412044.505253998.564257512.6617512.5795512090.002264069.004267750.7937750.7935612126.138274130.056277984.1377984.2655712152.695284181.251288212.9075812169.453294222.090298436.6245912176.191Dexpte4279.30612178.9bDVAMe4279.3060〛12178.900

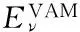
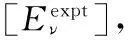
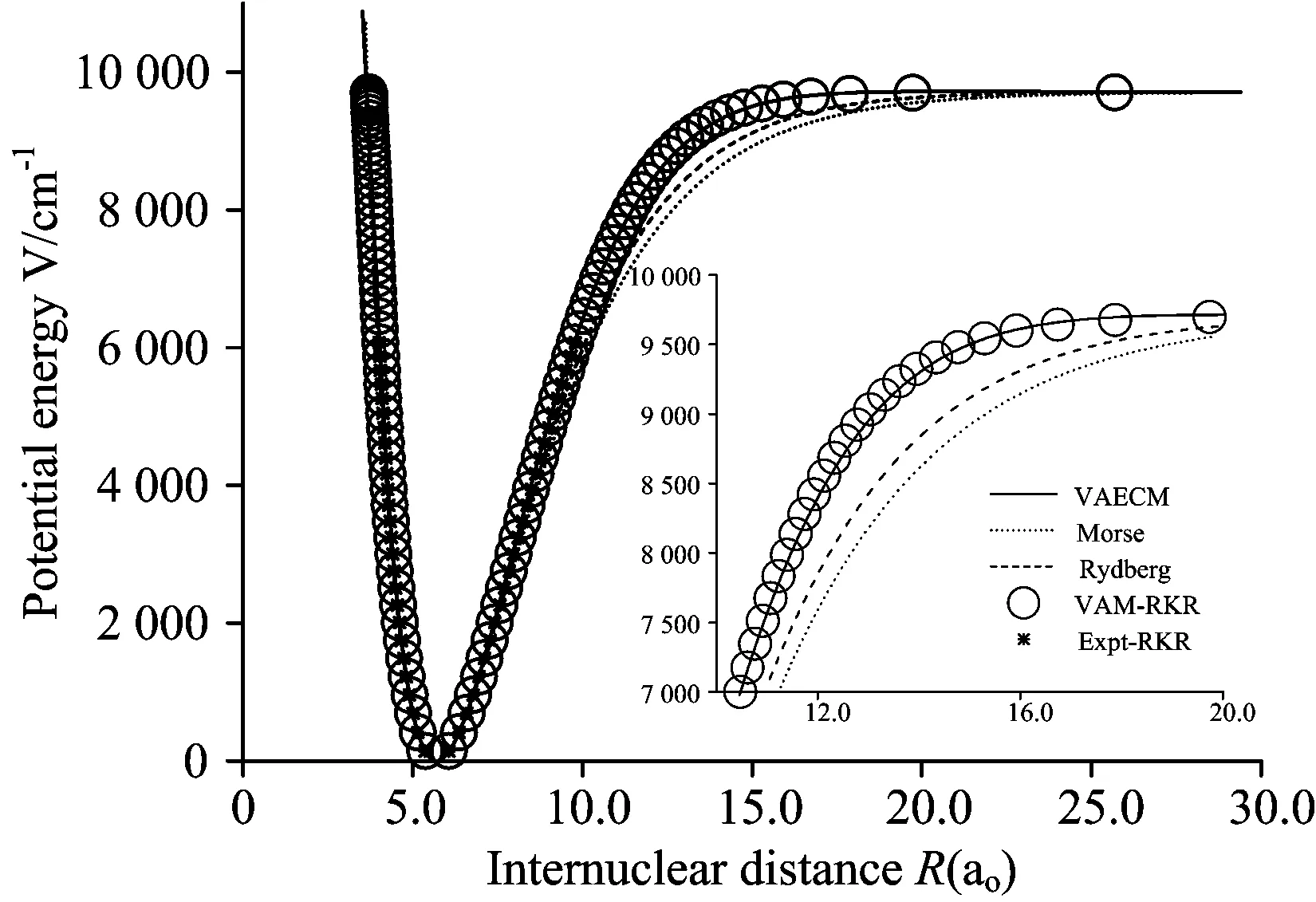
图1 Li2分子13Δg电子态势能曲线

○：VAM-RKR势； *：Expt-RKR势； ——：VAECM势变分参数λ=0.47； ……：Morse势； -----：Rydberg势

Fig.1 Potential energy curves (PECs) for the 13Δgstate of Li2

○：VAM-RKR data; *：Expt-RKR data; ──：VAECM potential withλ=0.47; ……：Morse potential; -----：Rydberg potential

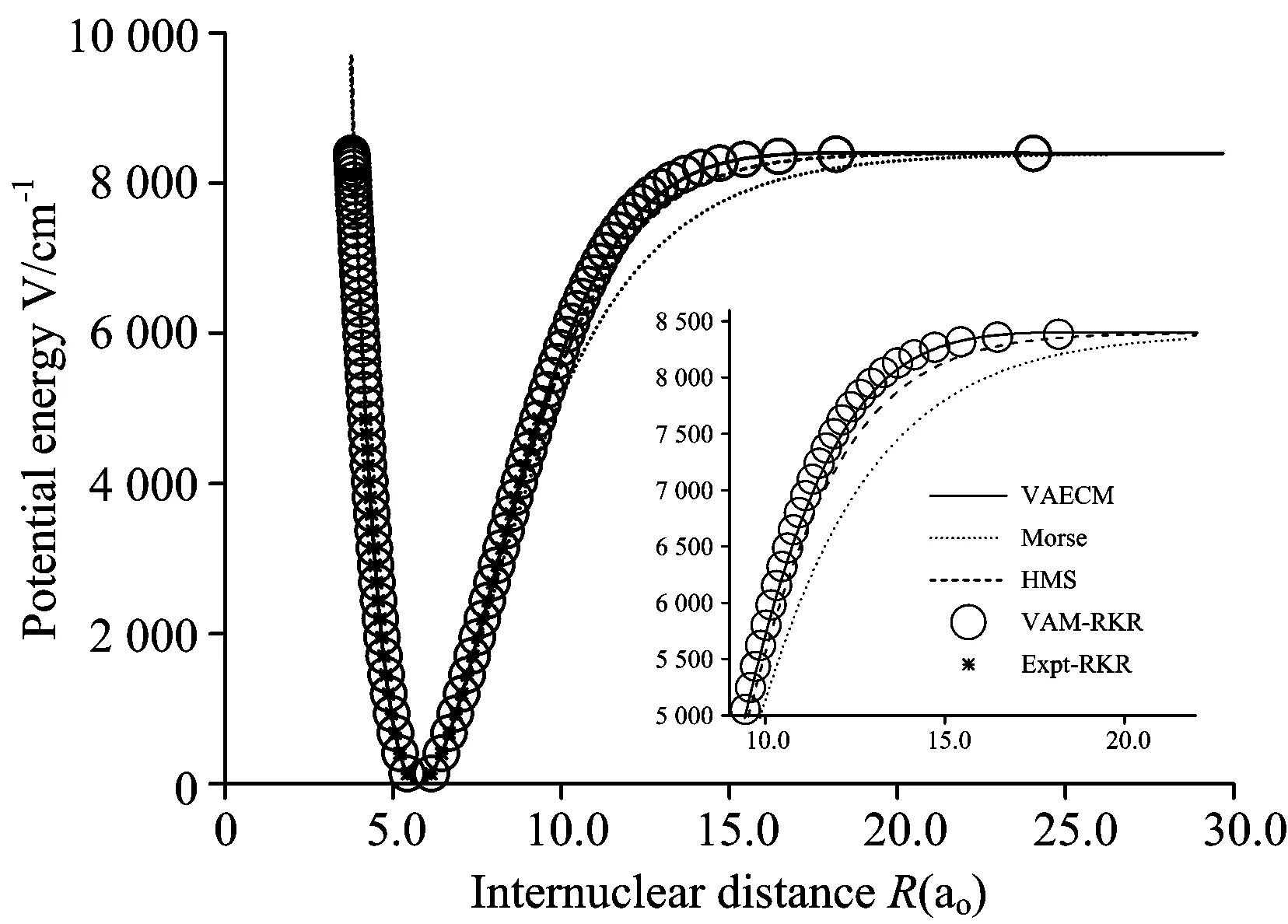
图2 Li2分子电子态势能曲线

○：VAM-RKR势； *：Expt-RKR势； ——：VAECM势变分参数λ=-2.43； ……：Morse势； -----：HMS势

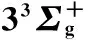
○：VAM-RKR data; *：Expt-RKR data; ──：VAECM potential withλ=-2.43; ……：Morse potential; -----：HMS potential

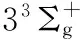
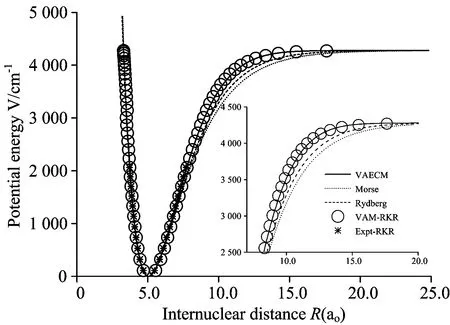
图3 Li2分子电子态势能曲线

○：VAM-RKR势； *：Expt-RKR势； ——：VAECM势变分参数λ=-1.10； ……：Morse势； -----：Rydberg势

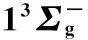
○：VAM-RKR data; *：Expt-RKR data; ──：VAECM potential withλ=-1.10; ……：Morse potential; -----：Rydberg potential

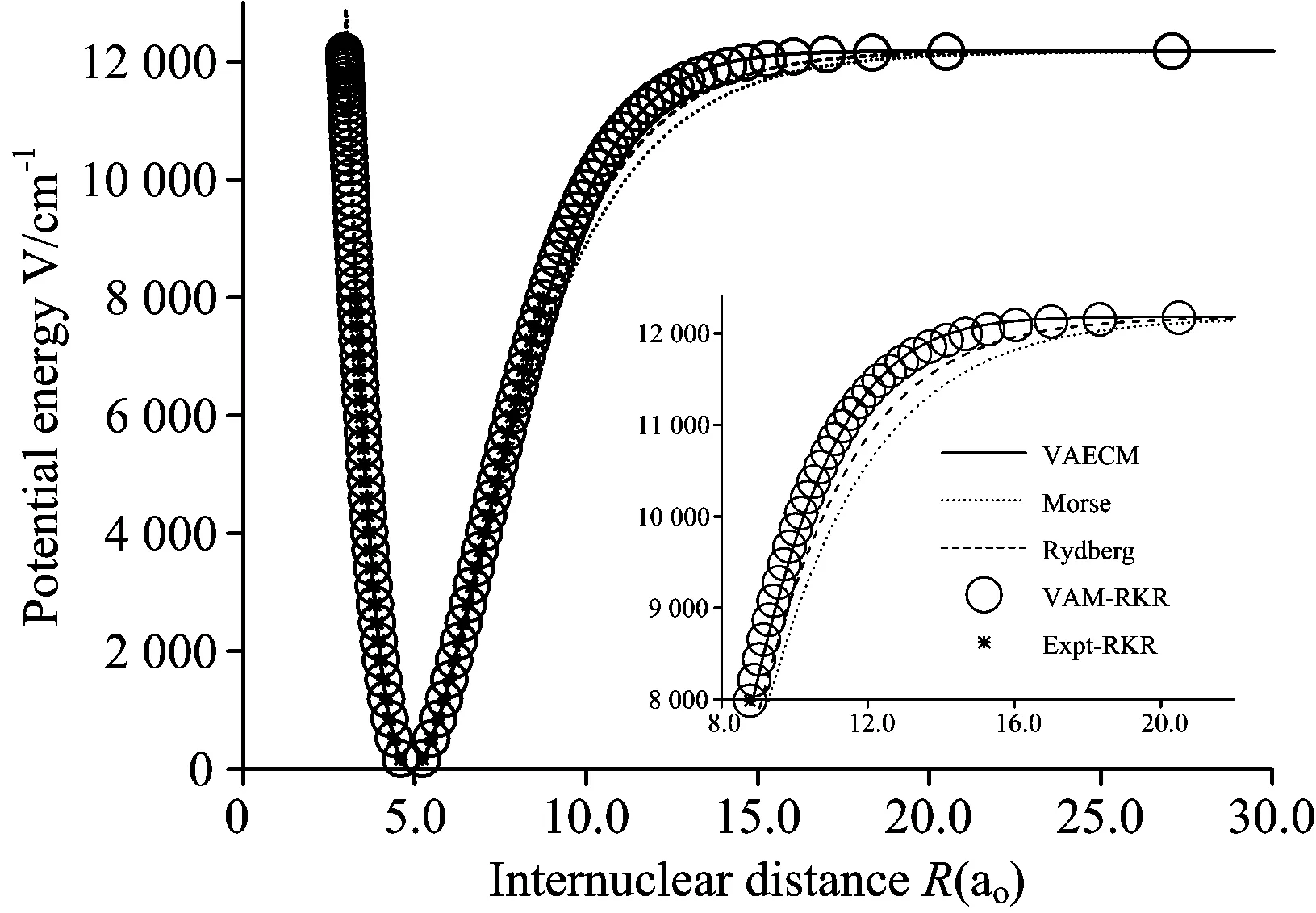
图4 Li2分子b3Πu电子态势能曲线

○：VAM-RKR势； *：Expt-RKR势； ——：VAECM势变分参数λ=-1.34； ……：Morse势； -----：Rydberg势

Fig.4 PECs for the b3Πustate of Li2

○：VAM-RKR data; *：Expt-RKR data; ──：VAECM potential withλ=-1.34; ……：Morse potential; -----：Rydberg potential

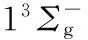
3 结论

[1] Miles R D,Morgus L,Kashinski D O,et al. J. Chem. Phys.,2006,125：154304.

[2] Le Roy R J,Dattani N S,Coxon J A,et al. J. Chem. Phys.,2009,131：204309.

[3] Dattani N S,Le Roy R J. J. Mol. Spectrosc.,2011,268：199.

[4] Matsunaga N,Zavitsas A A. J. Chem. Phys.,2004,120：5624.

[5] Herberg G(赫兹堡G). Molecular Spectra and Molecular Structure (Ⅰ)—Spectra of Diatomic Molecules(分子光谱与分子结构(第1卷)—双原子分子光谱). Translated by WANG Ding-chang(王鼎昌、译). Beijing: Science Press(北京：科学出版社),1983. 307.

[6] Jones K M,Maleki S,Bize S,et al. Phys. Rev. A,1996,54：1006.

[7] Liang Z,Tsai H L. J. Mol. Spectrosc.,2008,252: 108.

[8] Dai X C,Clevenger J O,Liu Y M,et al. J. Mol. Spectrosc.,2000,200：120.

[9] Song M,Yi P,Dai X C,et al. J. Mol. Spectrosc.,2002,215：251.

[10] Coxon J A,Melville T C. J. Mol. Spectrosc.,2006,235：235.

[11] Halls M D,Schlegel H B,DeWitt M. Chem. Phys. Lett.,2001,339：427.

[12] Sun Weiguo,Hou Shilin,Feng Hao,et al. J. Mol. Spectrosc.,2002,215：93.

[13] Sun Weiguo,Feng Hao. J. Phys. B: At. Mol. Opt. Phys.,1999,32：5109.

[14] Fan Qunchao,Sun Weiguo,Feng Hao,et al. Eur. Phys. J. D,2014,68,5.

[15] ZHANG Yi,SUN Wei-guo,FU Jia,et al(张燚、孙卫国、付佳、等). Acta Phys. Sin. (物理学报),2012,61(13)：133301-1.

[16] Zhang Yi,Sun Weiguo,Fu Jia,et al. J. Quant. Spectrosc. Radiat. Trans.,2013,120：81.

[17] Morse P M. Phys. Rev.,1929,34：57.

[18] Huxley P,Murrell J N. J. Chem. Soc. Faraday. Trans. Ⅱ,1983,79：323.

[19] Li D,Xie F,Li L,et al. J. Mol. Spectrosc.,2007,246：180.

[20] Yiannopoulou A,Ji B,Li L,et al. J. Chem. Phys. 1994,101：3581.

[21] Russier I,Yiannopoulou A,Crozet P,et al. J. Mol. Spectrosc.,1997,184：129.

[22] Schmidt-mink I,Muller W,Meyer W. Chem. Phys.,1985,92：263.

[23] Kaldor U. Chem. Phys.,1990,140：1.

Studies on the Analytical Potential Energies for Partial Electronic States of Li2with Variational Algebraic Energy Consistent Method

ZHANG Chun-guo1,FAN Qun-chao1*,SUN Wei-guo1,2,FAN Zhi-xiang2,ZHANG Yi2

1. School of Science,Research Center for Advanced Computation,Xihua University,Chengdu 610039,China 2. Institute of Atomic and Molecular Physics,Sichuan University,Chengdu 610065,China