基于并联装配模型的飞机壁板件装配偏差分析*

孙辉鹏，谭昌柏，安鲁陵，王志国

（南京航空航天大学机电学院，南京 210016）

飞机壁板件是构成机身的主要部件，其装配质量关系到飞机制造质量及性能，对其进行装配偏差分析进而提高装配质量具有重要意义。壁板件由大量弱刚性的柔性零件装配而成，在进行装配偏差分析时，不但要考虑刚体定位偏差的影响，还要考虑过约束定位及装配力作用下柔性变形的影响。

针对柔性件的装配偏差分析，需要借助有限元分析工具，早期的分析方法采用直接有限元蒙特卡洛仿真法，该方法简单明了，且每次计算中能够考虑贴合实际装配过程的有限元分析，从而得到更精确的结果，但由于有限元分析非常耗费时间，这种方法计算成本很高，难以在实际中运用。Liu和Hu[1]提出了影响系数法，该方法基于小变形、线弹性的假设，通过构建敏感度矩阵，建立零件偏差输入与装配体回弹偏差输出之间的线性关系，大大提高了柔性件装配偏差分析的效率；同时，Merkley[2]、Bihlmaier[3]、Mortensen[4]提出了线性接触模型，运用超元刚度矩阵方法来构建模型计算表达式，相较于通过单位力响应方法构建敏感度矩阵，超元刚度矩阵方法显得更为灵活高效。

柔性件装配过程可大致分为4步：定位、夹紧、焊（铆）接、回弹释放。Cai等[5]针对柔性件装配特点，提出了“N-2-1”定位方案，即柔性件在“3-2-1”确定性定位基础上，再施加“N-3”的过约束定位，该方案可有效降低柔性件在主平面内的法向变形。邢彦锋等[6]通过对两块薄板件的装配分析，进一步将柔性件装配过程细化为7个子过程，综合考虑了过约束定位及夹具释放方式对最终装配偏差的影响。Saadat等[7]运用有限元分析方法对机翼翼盒装配偏差进行了分析预测。Lin等[8]针对飞机壁板件包含大量同规格零件（如长桁、角片）的结构特点，提出了同类零件超元刚度矩阵快速生成的方法，在构建完成某一零件超元刚度矩阵的基础上，其他同规格零件的超元刚度矩阵只需做相应的转换即可得到，无需重复通过有限元分析工具生成，显著提高了分析效率。靳思源等[9]针对飞机壁板件装配工艺特点，提出一种刚柔混合的装配偏差建模方法。Cheng等[10-11]提出了一种面向自动钻铆过程的飞机薄壁件多工位铆接偏差模型。

目前，飞机壁板件装配偏差的分析基本按照定位、夹紧、铆接及回弹释放这4个经典步骤进行分析，而没有针对飞机壁板件的具体装配工艺建模，造成壁板件装配偏差模型构建不合理，从而导致分析过程不准确，分析结果偏离实际装配情况。本文将根据飞机典型壁板件装配工艺特点，首先建立壁板件典型装配工艺下的并联装配偏差模型，进而建立飞机壁板件装配偏差传递模型。最后，通过实际案例对所提出的装配偏差模型进行求解，并进行有限元仿真验证。

1 飞机壁板件典型装配工艺

飞机壁板件由数量众多的弱刚性钣金件（蒙皮、长桁、角片及钣金框）组成，其中蒙皮尺寸较大，这些零件装配时容易产生变形而导致装配偏差，所以需要使用专门的装配型架（夹具）进行定位夹紧，以确定各零件间的相对位置，防止零件变形，保证壁板件具有准确的尺寸和气动外形，如图1所示。

图1 壁板件装配Fig.1 Assembly of panel part

壁板件的具体装配工艺流程如下：

（1） 蒙皮通过工艺耳片安装在型架上，同时以内型卡板确定蒙皮内形，并在蒙皮的外表面用绑带将其夹紧；

（2） 长桁通过DA孔紧靠蒙皮内形定位，并用临时紧固件将长桁与蒙皮紧固；

（3） 角片通过DA孔紧靠蒙皮内形定位，并用临时紧固件将角片与蒙皮紧固；

（4） 在长桁、角片在蒙皮上定位后，将长桁与蒙皮、角片与蒙皮、角片与长桁进行铆接；

（5） 最后钣金框通过DA孔在相应的角片上进行定位并临时紧固，然后将钣金框与角片进行铆接。

其中，各组成零件DA孔设置如图2所示。

图2 组成零件DA孔设置Fig.2 DA hole setting of component part

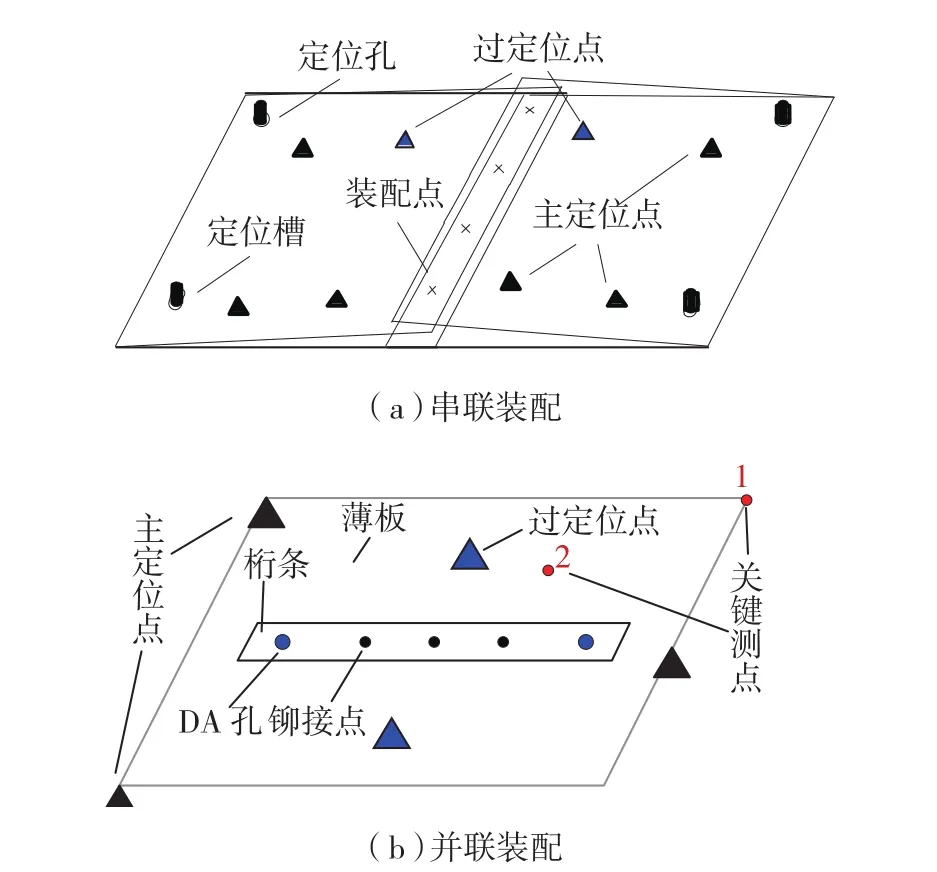
图3 柔性件装配模型Fig.3 Assembly model of flexible parts

2 飞机壁板件装配偏差建模

依据柔性件装配特点，可将其装配分为串联装配与并联装配，如图3所示，通常在对柔性薄板件装配偏差进行分析时，所用的装配模型都为串联装配模型，并将装配过程大致分为4步：定位、夹紧、铆接及释放回弹。但根据上述对飞机壁板件装配工艺的介绍可知，壁板件各零件间的装配基本为并联装配，零件间不是各自完成定位，而是通过DA孔实现相对定位，零件间的铆接也不是边缘搭接，而是其中一零件铆接到另一零件表面上，所以串联装配模型显然不能继续适用于壁板件的装配偏差分析，故本节将依据壁板件装配特点提出相应的并联装配模型，对其进行装配偏差分析建立并联装配偏差模型；在此基础上，按照壁板件装配顺序将其分解成许多相应的子装配过程，在依次对子装配进行偏差分析的基础上，即可建立壁板件装配偏差模型。

2.1 并联装配偏差模型

如图3（b）所示，并联装配模型以薄板与桁条装配为例，在综合考虑夹具偏差及其配置对最终装配偏差影响的基础上，将此模型的装配过程细化为6步，同时在小变形、线弹性假设的基础上依次对其进行装配偏差分析，主要分析薄板与桁条装配后其主平面的法向装配偏差，最终建立并联装配偏差模型，具体分析过程如下。

（1）薄板“3-2-1”刚体定位。

首先，薄板进行“3-2-1”刚体确定性定位，以确定其几何位置关系。如图4所示，薄板通过主定位点1、2、3进行确定性定位，考虑到桁条是通过DA孔与薄板实现相对定位的，这一阶段产生的薄板定位偏差不会对薄板与桁条的最终装配偏差造成影响，故不计入此阶段的定位偏差。

（2）薄板“N-3”过约束定位。

由于薄板的弱刚性特点，为减小其主定位平面内的法向变形，需对薄板进行额外的“N-3”过约束定位，从而实现薄板的“N-2-1”定位（如图5所示）。在薄板主平面上施加额外的“N-3”个夹持力将该点夹持到所对应过约束定位位置，此时薄板在夹持力的作用下势必会产生柔性变形，导致薄板偏差源（DA定位孔、铆接点、关键测点）处的偏差发生变化。

设薄板过约束定位点处的法向制造误差为VAe=[VAe1，VAe2]，考虑额外过约束定位偏差Ve=[Ve1，Ve2]的影响，则薄板在过约束定位点处的夹持位移可表示为：

图4 薄板“3-2-1”定位Fig.4 "3-2-1" location of sheet metal

图5 薄板过约束定位Fig.5 Over constrained location of sheet metal

图6 桁条DA孔定位Fig.6 DA hole location of stringer

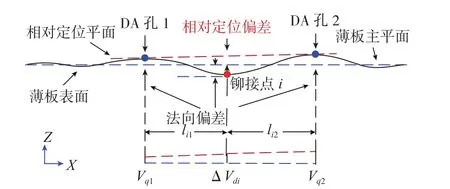
图7 DA孔相对定位偏差Fig.7 Relative locating variation of DA holes

在夹持力Fe=[Fe1，Fe2]的作用下，薄板偏差源处 的 法 向 变 形 量 为 ∆Vse=[∆Veq，∆Vem，∆Vek]，其 中∆Veq=[∆Veq1，∆Veq2]为薄板 DA 孔处的法向变形量，∆Vem=[∆Vem1，∆Vem2， ∆Vem3]为薄板铆接点处的法向变形量，∆Vek=[∆Vek1，∆Vek2]为薄板关键测点处的法向变形量，则根据柔性件受力与变形之间的关系得：

其中，KAe为超元刚度矩阵，其边界条件为薄板“3-2-1”定位。

（3）桁条通过DA孔定位。

如图6所示，桁条通过DA孔紧贴薄板表面进行定位，并进行临时紧固，以实现了桁条与薄板的相对定位。当薄板在DA孔处存在法向偏差时，会造成桁条与薄板的相对定位偏差（如图7所示）。设桁条与薄板DA孔相对定位时不发生表面接触干涉，则铆接点i处产生的相对定位偏差可表示为：

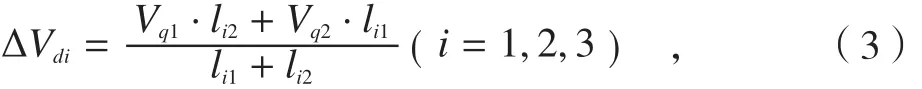
其中,li1、li2分别为铆接点i在主平面内距DA孔1、2的长度；Vq=[Vq1，Vq2]为薄板DA孔处的法向偏差，且有Vq=VAq+ ∆Veq；VAq= [VAq1，VAq2]为薄板 DA 孔处的法向制造误差。将公式（3）改写成矩阵形式，可表示为：

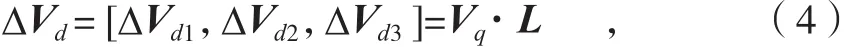
其中

设薄板与桁条对应铆接点处在主平面内法向制造误差分别为VAm=[VAm1，VAm2，VAm3]和VBm=[VBm1，VBm2，VBm3]，则桁条通过DA孔在薄板表面上定位后，铆接点i处以薄板表面为基准的铆接偏差可表示为Vmi=∆Vdi+VAmi+VBmi+ΔVemi（i=1，2，3），即有：

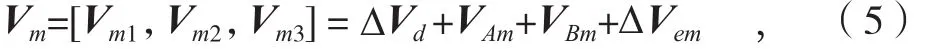
此阶段桁条通过DA孔定位，只是确定了桁条的几何位置关系，包括其与薄板的相对位置，桁条与薄板不会产生变形。

（4） 薄板与桁条进行夹紧铆接。

如图8所示，施加额外夹紧力将桁条铆接点夹紧到薄板对应铆接点处，然后进行铆接。为便于夹紧力的计算，设桁条与薄板夹紧铆接时桁条在DA孔处夹持固定住，DA孔处的支反力将在下一步中进行释放。

图8 夹紧铆接Fig.8 Clamping and riveting

设铆接点处的夹紧力为Fm=[Fm1，Fm2，Fm3]，桁条在DA孔处夹持固定住，其支反力为Fq=[Fq1，Fq2]，则根据柔性件受力与变形之间的关系得：

其中，KBc为超元刚度矩阵，其边界条件为桁条在DA孔处夹持固定住。同时通过有限元分析软件可以求得夹紧力Fm与支反力Fq的关系，可表示为：

其中，Cqm为夹紧力与支反力之间的关系矩阵。

（5） 铆接夹紧及DA孔处的固定夹持释放。

当桁条与薄板铆接完成后，桁条DA孔处的固定夹持撤销，铆接夹紧释放，而此时薄板与桁条已组成装配体，其刚度发生变化。为模拟释放回弹变形，需在装配体的铆接处施加回弹力Frm及Frq，其中Frm= [Frm1，Frm2，Frm3]，Frq= [Frq1，Frq2]，如图9所示。回弹力大小分别等于铆接夹紧力、夹持支反力，方向相反，即有：

在回弹力的作用下，薄板与桁条所组成的装配体会发生回弹变形，此时需要关注薄板上关键测点的变形量，根据柔性件受力与变形之间的关系可得：

图9 释放回弹Fig.9 Release and springback

其中，∆Vrq= [∆Vrq1，∆Vrq2]为 DA 孔处的变形；∆Vrm=[∆Vrm1，∆Vrm2，∆Vrm3]为铆接点处的变形；∆Vrk= [∆Vrk1，∆Vrk2]为薄板关键测点处的变形；Krk为超元刚度矩阵，其边界条件为装配体“N-2-1”定位。

（6） 装配体释放“N-3”过约束定位。

此时装配体处于“N-2-1”过约束定位状态，释放原来对薄板的“N-3”过约束定位后，装配体处于“3-2-1”确定性定位，故为完全释放，这种释放方式可消除重定位偏差，与测量基准相一致。为模拟装配体回弹变形，在原来薄板过约束定位点处施加相应的回弹力Fu=[Fu1，Fu2]，回弹力大小等于原来过约束定位处施加的夹持力，方向相反（如图10所示），即有：

在回弹力的Fu作用下，装配体产生回弹变形，此时需要关注装配体中薄板表面上关键测点的法向变形量，由柔性件受力与变形之间的关系可得：

其中，∆Vue=[∆Vue1，∆Vue2]为过约束定位点处的法向变形量，∆Vuk=[∆Vuk1，∆Vuk2]为装配体中薄板表面上关键测点处的法向变形量，Kuk为超元刚度矩阵，其边界条件为装配体“3-2-1”定位。

图10 过约束释放Fig.10 Over constrained release

至此，由上述对模型装配过程的分析，可以建立零件制造误差、夹具定位偏差与最终装配偏差之间的关系，继而建立并联装配偏差模型（如图11所示），最终装配偏差由装配过程各阶段变形叠加而成，所关注的关键测点的法向装配偏差为：

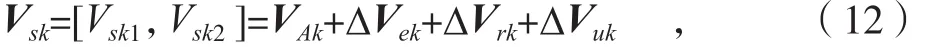
其中，VAk为关键测点的法向制造误差，∆Vek、∆Vrk及∆Vuk分别由公式（2）、（9）及（11）求得。

2.2 壁板件装配偏差模型

按照壁板件装配顺序，将其装配过程分解为多个子装配过程，针对各个子装配过程运用上述所提出的并联装配偏差模型进行装配偏差分析，其装配偏差输出作为下一个子装配的偏差输入，如图12所示，整个分析过程可以表示为：

其中，V为偏差源矩阵，包括每个装配零件上铆接点、DA孔及关键测点的偏差，上标表示其所处装配阶段；pi表示第i个子装配偏差分析函数，即运用并联装配偏差传递模型对第i个子装配进行装配偏差分析，其输出为V（i）；F为夹具装配偏差矩阵；n表示共有n个子装配过程。

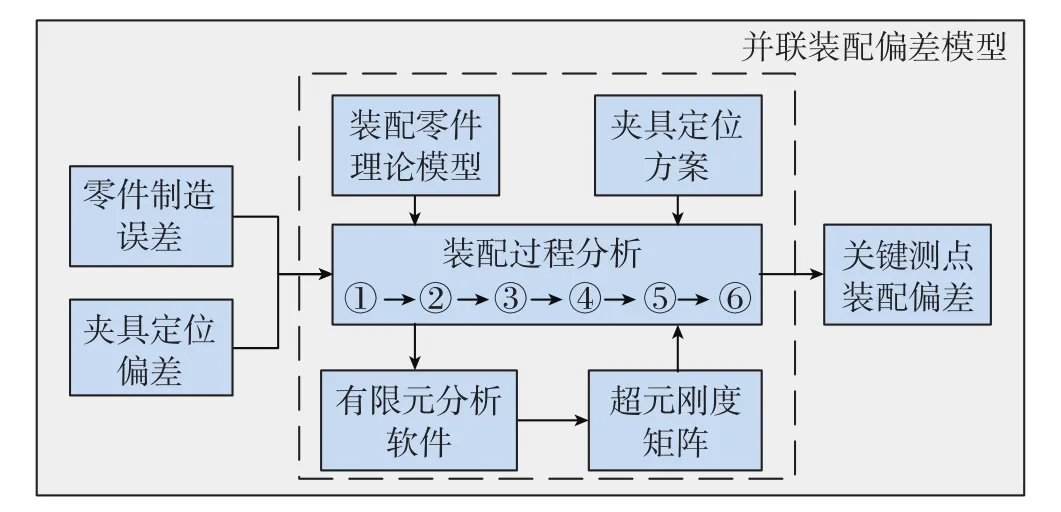
图11 并联装配偏差模型Fig.11 Assembly variation model in parallel

图12 壁板件装配偏差模型Fig.12 Assembly variation model of panel part

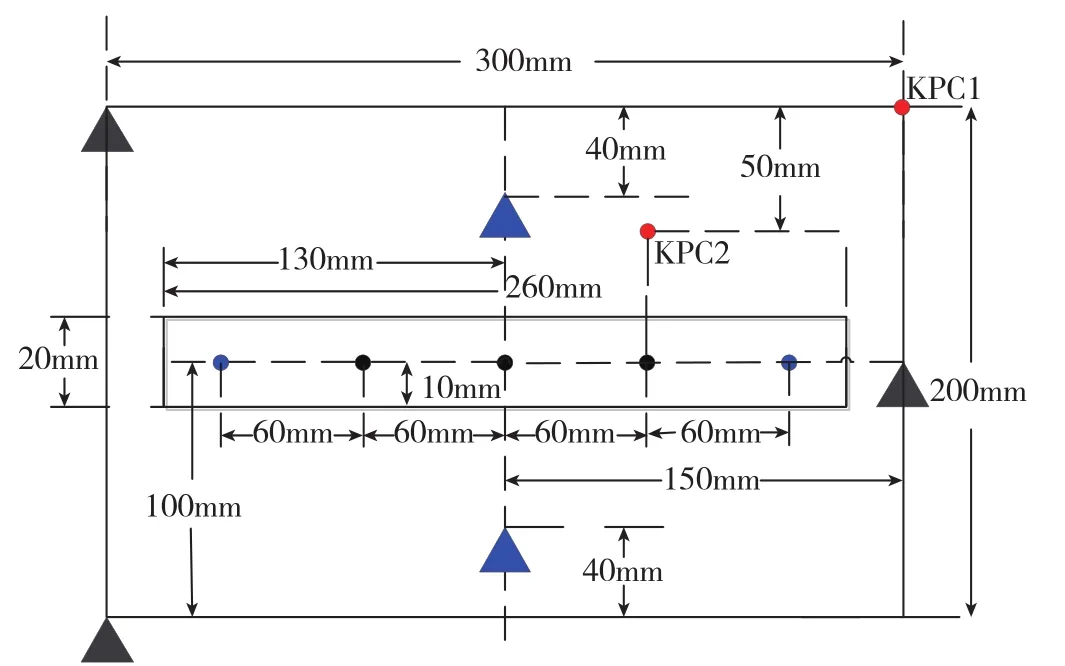
图13 并联装配模型尺寸示意图Fig.13 Size diagram of the assembly model in parallel

表1 零件材料属性

表2 偏差源设定 mm

3 案例研究

针对以上提出的并联装配偏差模型及壁板件装配偏差模型，本节将借助有限元分析软件——ABAQUS，对具体案例模型进行超元刚度矩阵提取，然后进行偏差模型计算；同时运用ABAQUS对该具体案例模型进行有限元仿真装配；然后将偏差模型计算偏差值与有限元仿真装配偏差值进行对比分析。

3.1 并联装配模型偏差分析

如图13所示所选用的并联装配模型包括夹具定位位置、铆接点及DA孔位置，以及薄板上选取的关键测点位置。薄板和桁条都为铝合金，其材料属性如表1所示。定义4组（A1、A2、B1、B2）偏差源输入，其中偏差源包括零件在DA孔、铆接点、过约束定位点及关键测点处的制造误差，以及夹具过约束定位偏差，不失一般性，设零件制造误差只存在于薄板上，桁条无制造误差，如表2所示。

依据并联装配偏差模型，对上述案例模型进行求解。公式中所需的超元刚度矩阵KAe、KBc、Krk及Kuk运用有限元分析软件ABAQUS进行提取，如图14所示。其计算结果如表3所示。

同时运用有限元分析软件ABAQUS，依据表2中的偏差输入建立实际偏差模型，并对其进行有限元仿真装配，然后输出关键测点的装配偏差（如图15所示），仿真结果如表4所示。

将表3中与表4中的结果进行对比，发现本文提出的并联装配偏差模型计算结果的变化趋势及数值与有限元仿真装配结果值相近，进而证明了其有效性。

图14 并联模型超元刚度矩阵提取Fig.14 Super element stiffness matrix extraction of the parallel model

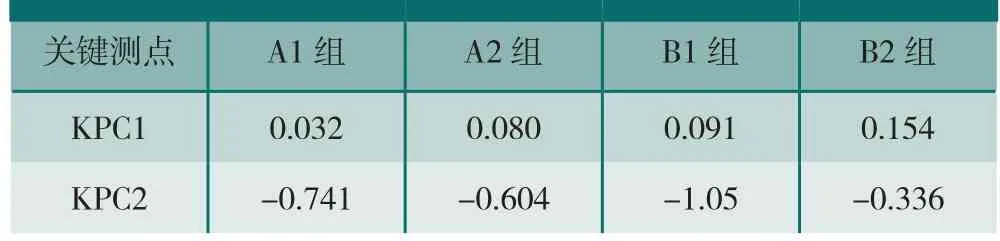
表3 关键测点装配偏差计算值 mm

图15 并联模型有限元仿真装配应变云图Fig.15 Assembly strain contour of FEM for the parallel model

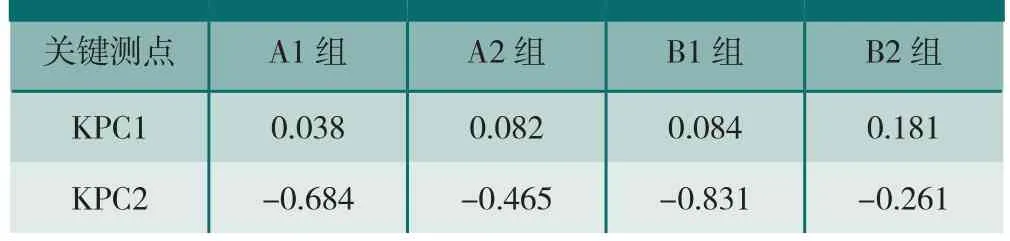
表4 关键测点仿真装配偏差值 mm

表5 零件材料属性

图16 蒙皮尺寸偏差Fig.16 Dimensional deviation of skin

表6 卡板工作型面定位偏差 mm

3.2 壁板件装配偏差分析

壁板件由蒙皮、长桁、角片及钣金框组成，都为铝合金材料，其中蒙皮为单曲率，半径为1990mm，长为2000mm，宽为1917mm，各组成零件的材料属性如表5所示。

壁板件装配偏差源包括零件制造误差及夹具定位偏差。壁板件组成零件都为钣金件，制造成形精度不高，不失一般性，此处主要考虑蒙皮的制造误差，如图16所示蒙皮截面，其上下两端法向偏差为2mm；夹具定位偏差主要考虑内型卡板工作型面的定位偏差，即过约束定位偏差，将卡板工作型面等效为9个过约束定位点，从上到下依次编号，案例模型中共包含两个卡板，设其定位偏差一致，如表6所示。

壁板件组成零件众多，为简化案例模型，只选取其中的5根长桁、4个角片及1个钣金框，如图17所示。按照壁板件装配工艺将其装配过程分为10个子过程（蒙皮→长桁1→长桁2→长桁3→长桁4→长桁5→角片1→角片2→角片3→角片4→钣金框），根据如图12所示的壁板件装配偏差模型进行装配偏差分析，每个子过程的分析根据图11所示的并联装配偏差模型进行求解。

同时，运用有限元分析软件ABAQUS对上述壁板件案例模型进行仿真装配，仿真过程同样按照壁板件的装配顺序依次进行，各个子过程的仿真装配应变云图如图18所示。

如图17中所示，以壁板件四个端点为关键测点，依照壁板件装配的10个子过程分别通过壁板件装配偏差模型求解和有限元仿真装配得到各个阶段关键测点的法向装配偏差，并对其进行结果对比，如图19所示，4个关键测点的模型求解结果与仿真装配结果基本吻合，从而验证了壁板件装配偏差模型的有效性。

图17 壁板件装配模型Fig.17 Assembly model of panel part

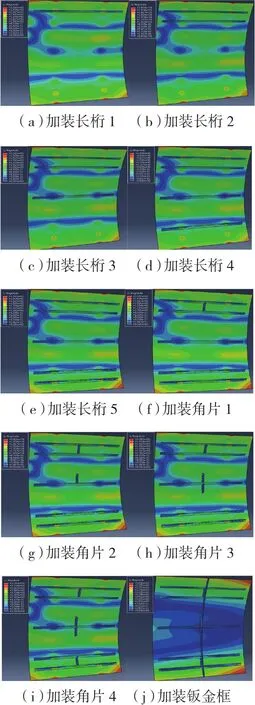
图18 壁板件仿真装配应变云图Fig.18 Assembly strain contour of FEM for panel part

图19 壁板件关键测点法向装配偏差结果对比Fig.19 Comparison of the results of assembly variation in the normal direction on the key points of panel part

4 结束语

本文针对壁板件装配工艺特点，提出了壁板件组成零件典型装配的并联装配模型，在小变形、线弹性假设的基础上，将其装配过程细分为6个子过程分别进行了装配偏差分析，建立了并联装配偏差模型，在此基础上，依照壁板件装配顺序建立了壁板件装配偏差模型；最后以具体案例模型分别验证了并联装配偏差模型和壁板件装配偏差模型的有效性，为飞机薄壁类结构部件的装配偏差分析及预测提供了理论及技术手段。

[1]LIU S C, HU S J. Variation simulation for deformable sheet metal assemblies using finite element methods[J]. Journal of manufacturing science and engineering, 1997, 119(3):368-374.

[2]MERKLEY K G. Tolerance analysis of compliant assemblies[D].Provo: Brigham Young University, 1998.

[3]BIHLMAIER B F. Tolerance analysis of flexible assemblies using finite element and spectral analysis[D]. Provo: Brigham Young University, 1999.

[4]MORTENSEN A J. An integrated methodology for statistical tolerance analysis of flexible assemblies[D]. Provo: Brigham Young University, 2002.

[5]CAI W, HU S J, YUAN J X. Deformable sheet metal fixturing:principles, algorithms, and simulations[J]. Journal of Manufacturing Science and Engineering, 1996, 118(3):318-324.

[6]邢彦锋, 赵晓昱, 吴伟蔚. 基于夹具配置的薄板件装配偏差分析模型[J]. 计算机集成制造系统, 2010,16(2):280-286.

XING Yanfeng, ZHAO Xiaoyu, WU Weiwei. Assembly variation analysis model based on fixture configurations for sheet metal parts[J].Computer Integrated Manufacturing Systems, 2010, 16(2):280-286.

[7]SAADAT M, SIM R, NAJAFI F. Prediction of geometrical variations in airbus wingboxassembly[J]. Assembly Automation, 2007,27(4):324-332.

[8]LIN J, JIN S, ZHENG C, et al. Compliant assembly variation analysis of aeronautical panels using unified substructures with consideration of identical parts[J]. Computer-Aided Design, 2014, 57:29-40.

[9]靳思源, 沈利冰, 金隼, 等. 飞机壁板件装配偏差的刚柔混合建模方法与应用[J]. 机械设计与研究, 2013, 29(3):58-61.

JIN Siyuan, SHEN Libing, JIN Sun, et al. Rigid-flexible hybrid modeling method and application of airplane wall plate assembling deviation[J]. Machine Design and Research, 2013, 29(3):58-61.

[10]CHENG H, LI Y, ZHANG K, et al. Efficient method of positioning error analysis for aeronautical thin-walled structures multistate riveting[J]. The International Journal of Advanced Manufacturing Technology, 2011, 55(1-4):217-233.

[11]CHENG H, LI Y, ZHANG K, et al. Variation modeling of aeronautical thin-walled structures with multi-state riveting[J]. Journal of Manufacturing Systems, 2011, 30(2):101-115.