CFRP索斜拉桥地震波行波效应分析

杨吉新， 马璐珂， 高 辉， 黎建华， 刘 佩

(1.武汉理工大学 交通学院，湖北 武汉 430063；2.中国市政工程中南设计研究总院有限公司,湖北 武汉 430010)

CFRP索斜拉桥地震波行波效应分析

杨吉新1， 马璐珂1， 高 辉1， 黎建华1， 刘 佩2

(1.武汉理工大学 交通学院，湖北 武汉 430063；2.中国市政工程中南设计研究总院有限公司,湖北 武汉 430010)

碳纤维增强聚合物(CFRP)具有轻质、高强、耐腐蚀、耐疲劳等优良性能，在大跨度桥梁中将会广泛应用。对跨度大或延迟时间长的结构需考虑行波效应的影响，且其对CFRP索斜拉桥和普通斜拉桥影响程度也不相同。因此，为研究CFRP索斜拉桥在地震波行波效应下的动力性能，以某一大跨度斜拉桥为背景，建立模型，按照等强度原则将钢索换为CFRP索，计算并获得CFRP索斜拉桥在地震波一致激励和多点激励作用下的位移、应力及分别对应的时程曲线。计算结果表明，行波效应对CFRP索斜拉桥地震响应有显著的影响，使得该桥的时程曲线发生了较显著的变化，塔根效应增加显著，结构部分位移增长非常显著，对轴力影响比对剪力的影响更为明显，因此在大跨度CFRP索斜拉桥的设计分析中必须考虑行波效应的影响。

CFRP索斜拉桥；行波效应；地震响应分析；有限元

随着桥梁的发展,其跨度越来越大,而碳纤维增强聚合物(CFRP)具有轻质、高强、耐腐蚀、耐疲劳等优良性能[1],能够解决桥梁跨度增大的诸多问题,将广泛应用于大跨度桥梁中。地震波的传播速度是个有限值, 到达结构不同支座时发生时间延迟,对跨度大或延迟时间长的结构,需考虑行波效应的影响。

1982年项海帆教授[2]对天津永和斜拉桥进行了考虑行波效应的地震反应分析,计算结果表明塔顶位移在有相位差时减小,并呈周期性变化,因此得出由于非一致激励输入引起动力位移互相抵消和行波效应对漂浮体系的斜拉桥有利的结论。陈幼平和周宏业[3]再次以永和桥为例,其结果却与前者有较大出入,即行波效应可能使斜拉桥地震反应显著增大,塔根弯矩可增大1倍,主梁轴力可增大6～10倍,因此斜拉桥的行波效应可能对结构的破坏有十分重大的影响。Ghaffar AM和Nazmy AS等[4-7],张翠红[8],武芳文[9]分别对不同跨度的斜拉桥进行了考虑行波效应的地震反应分析,并比较与一致地震动作用的结构响应进行对比、分析。

由此看出,对于斜拉桥的行波效应研究得出的结果还不是很一致,不同的研究者常常得出不同甚至完全相反的结论,而地震波行波效应对钢索斜拉桥和CFRP索斜拉桥影响程度不同,现阶段对CFRP索斜拉桥的行波效应研究比较少,因此有必要对CFRP索斜拉桥的行波效应进行分析,以确定地震波行波效应对CFRP索桥梁的影响。

1 模型概况

本文以肇庆市阅江大桥为背景,以其结构为参照,建立模型。其位于广东省中西部肇庆市,呈南北向横跨于西江河上,连接肇庆市和高要市,河宽约1 500 m,桥型采用单索面预应力混凝土斜拉桥方案,主桥跨径布置为160 m+320 m+160 m,墩、塔、梁固结。主梁采用单箱五室预应力混凝土箱型截面,箱顶宽度33.5 m,梁高3.7 m;塔柱下部为实心混凝土结构,上部拉索锚固区及拉杆采用钢结构;斜拉索采用1 670 MPa级斜拉索,采用双层HDPE防护低应力平行热镀锌钢丝拉索和冷锚固;桥梁的设计基准年为100 a,地震动峰值加速度为0.05g。本文以肇庆阅江大桥为基本模型,分析CFRP索斜拉桥在考虑行波效应地震作用下动力性能。

2 计算模型

根据阅江大桥,建立有限元分析模型。由于拉索下部固结在梁处,其受力不仅仅是轴向力,因此全桥模型均采用梁单元beam3。根据背景桥梁的情况,不同位置选用不同的材料特性和单元特性。x、y轴分别表示桥梁横向和竖向。梁两端只约束竖向位移,墩底约束横竖向位移。为研究CFRP索斜拉桥的动力特性,将实际桥梁中的钢索替换为CFRP索,替换采用等轴向强度原则,即,Acσc=Asσs(σ为材料的容许应力),同时考虑垂度的影响,选用恩斯特公式[10]对拉索的弹性模量进行换算,换算前后材料特性如表1所列。

表1 钢索与CFRP索材料特性

3 研究方法与原理

3.1 行波效应分析方法

行波效应分析方法有三种:直接加速度法,大质量法和位移输入法。地震动的输入模式直接关系到地震反应分析的结果,要根据实际情况慎重选取。

(1) 直接加速度法:将加速度记录直接施加在整个结构上进行瞬态动力学分析,它是最简单最精确的一种方法,可以同时施加各种荷载,一般不会出现收敛困难的问题,但是因为加速度的输入只能施加在整个结构上而不能有选择地施加在结构单元或节点上,所以只能进行一致激励分析。

(2) 大质量法[11]:在结构的支承点上,建立一个单元点质量单元,给这一节点单元设定很大的质量,通常为结构总质量的106以上,使得结构的质量相对于大质量可以忽略,然后利用大质量的惯性力将地震荷载施加到需要激励的目标结构上。进行动力分析时,放松支承节点相应激励方向的自由度约束,然后在支承节点激励方向施加很大的力,这个力为质量单元的质量与地面加速度的乘积。通过这个方法,可间接地把地面加速度施加到墩底节点上。这种方法的优点是可以方便施加多点激励。缺点是质量阻尼系数再乘上质量矩阵后会在系统中产生很大的阻尼力,这将导致地震动输入的不精确,从而导致系统响应的不精确;当结构上同时作用重力荷载、预应力荷载等时,非线性分析容易遭遇收敛困难。此外,当地震动输入为行波或多点激励时,采用这种方法不易得结构的相对位移响应。

(3) 位移输入法:把位移时程记录施加在各基础节点上,这种方法较之大质量法简单,可方便施加多点激励,可直接得到结构的相对位移响应,且可以同时施加各种荷载,一般不会出现收敛困难的问题。地震波加速度记录比较容易获得,而地面位移记录不易获得,通常是通过加速度记录转化而来,精度较差。这样一来,给结构施加位移记录,容易导致加速度的不连续,从而导致结构响应的不精确。

上述三种模式各有优缺点,直接加速度法比较精确但不能输入多点激励,其余两种方法可输入多点激励但系统响应的精确性相对较差。

3.2 计算原理

位移输入法精度满足计算要求,且形式简单、计算方便,故本文采用位移输入法进行地震波的输入。

将结构自由度位移分为非支承处的自由度位移xs和支承处的自由度位移xb,结构平衡方程为

(1)

Kss为非支承处的自由度刚度矩阵,Kbb为支承处的自由度刚度矩阵,Ksb、Kbs为两者耦合自由度刚度矩阵。Rs为外部荷载,Rb为支座反力。

地震动反应的实质是地震在基底引起的位移对上部结构的反应,但是由于结构的质量和位移会产生惯性力,所以结构的动力平衡方程[12]如下:

(2)

方程可简化为

(3)

xb为地面运动位移向量,对于多点激励不同基底有不同位移向量。

4 斜拉桥时程计算分析

本次计算基本假定如下:① 行波激励采用修正后的天津波,地震动输入采用位移输入法,采用软件SeismoSignal对加速度时程波进行积分得到位移时程波。地震波时程变化如图1所示。② 假定地震波从左桥塔侧向右桥塔侧传播,为了同时考虑波速的影响, 根据斜拉桥相邻桥墩之间距离,计算地震波传播速度分别为150、300、500、1 000、2 000、10 000、40 000 m/s, 求得各墩输入的迟滞时间后输入位移时程波对应的时程分析结果,不考虑斜拉桥的几何非线性后的地震响应。③ 该桥跨径较大,故只考虑了桥纵向行波效应,横向及横向与纵向的组合不予以考虑,且行波效应只考虑主塔支承处地震波相位变化的影响规律,没有考虑地震波在传播过程中的频散、振幅衰减、波形变化。

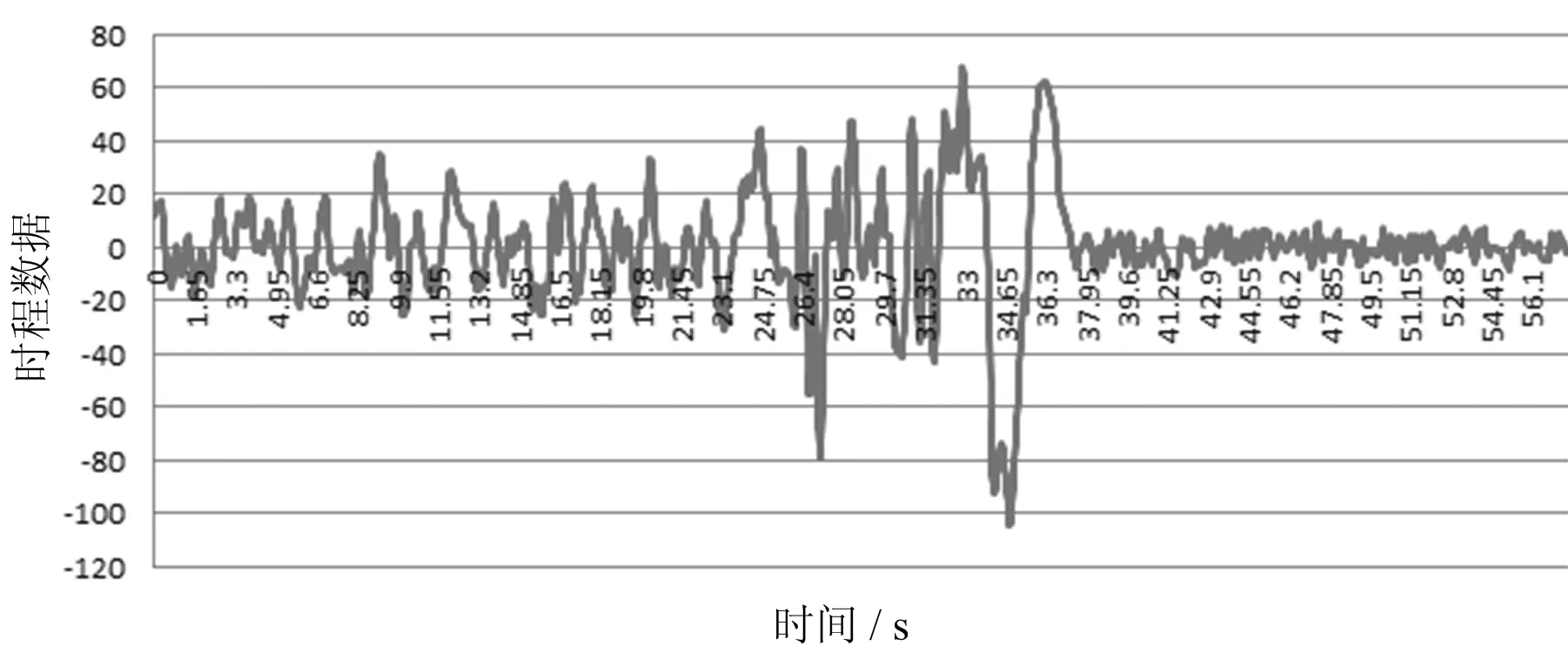
图1 天津波时程数据图

4.1 时程分析结果

CFRP索斜拉桥在调整后纵向天津波的激励下,不同视波速和一致激励下斜拉桥地震反应桥梁关键截面位移对比如表2、表3所列。

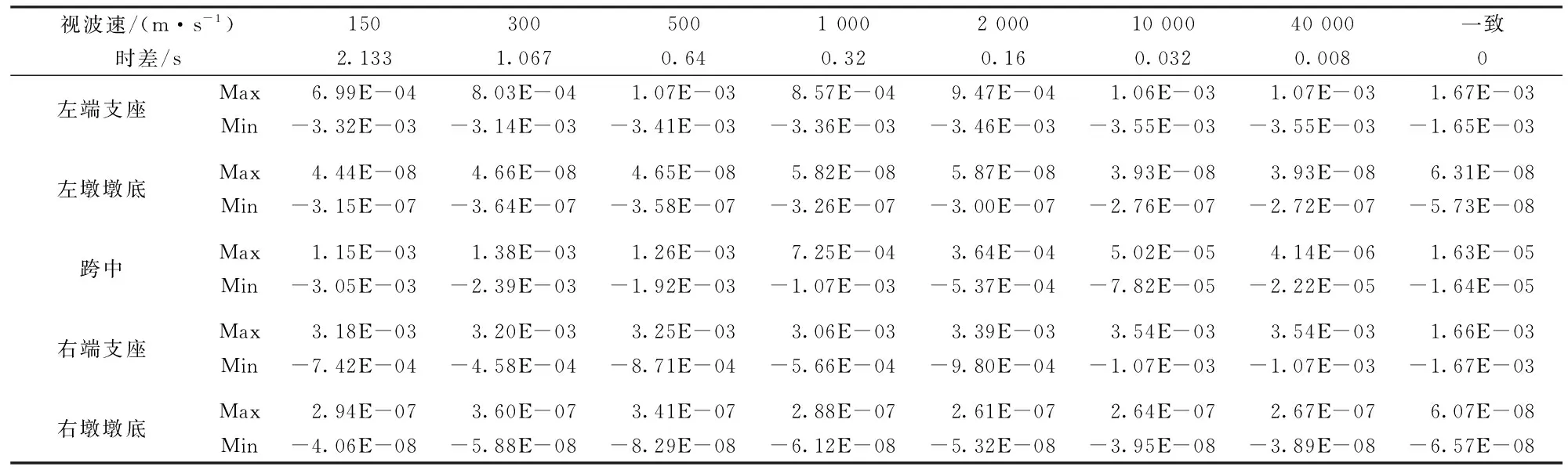
表2 CFRP索斜拉桥行波效应横向位移 m

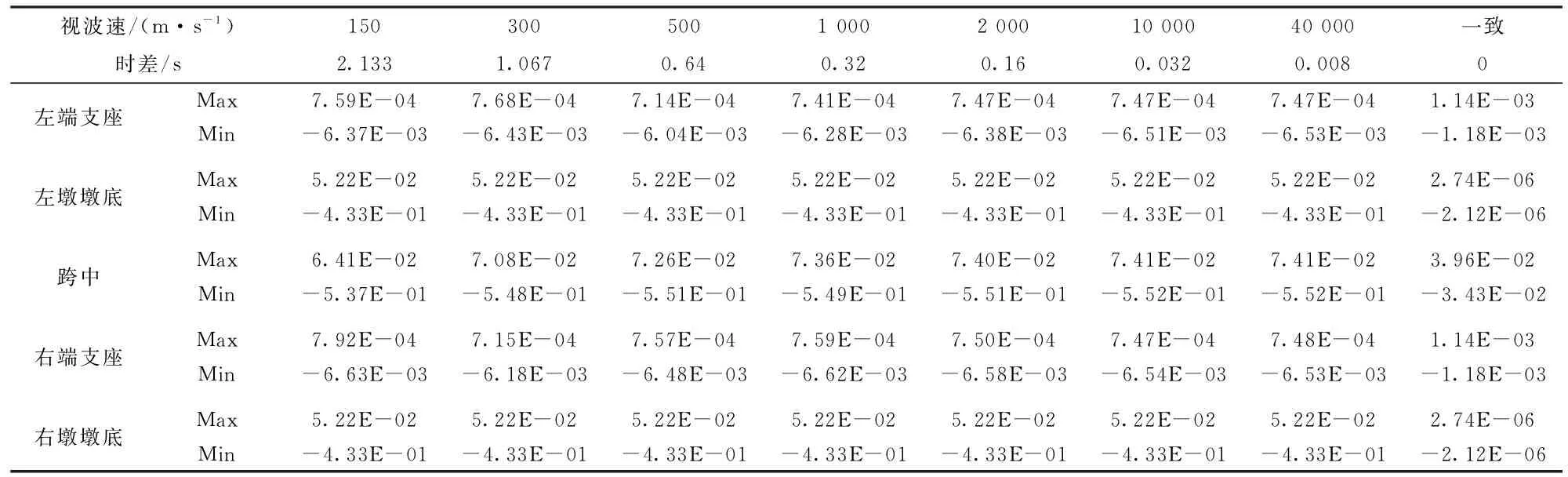
表3 CFRP索斜拉桥行波效应纵向位移 m

关键截面行波效应位移时程曲线如图2所示(以跨中、右支座、右墩墩底为例进行说明)。

图2 CFRP索斜拉桥位移时程曲线

关键截面轴向应力和剪切应力的结果如表4、表5所列。

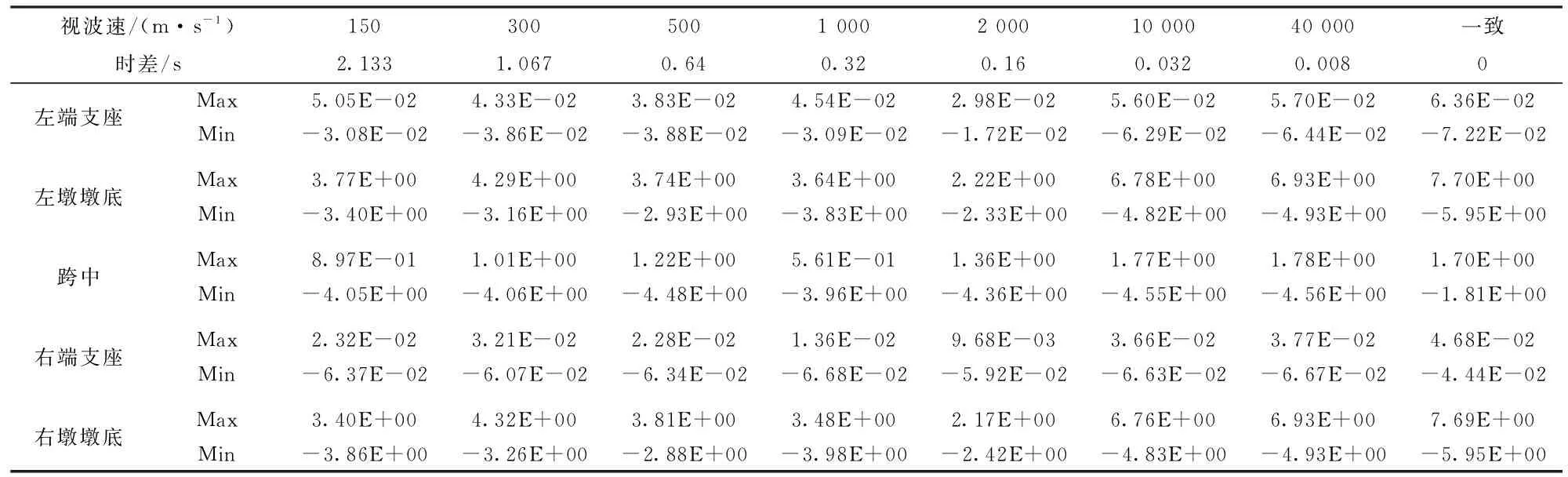
表4 CFRP索斜拉桥行波效应轴向应力 MPa

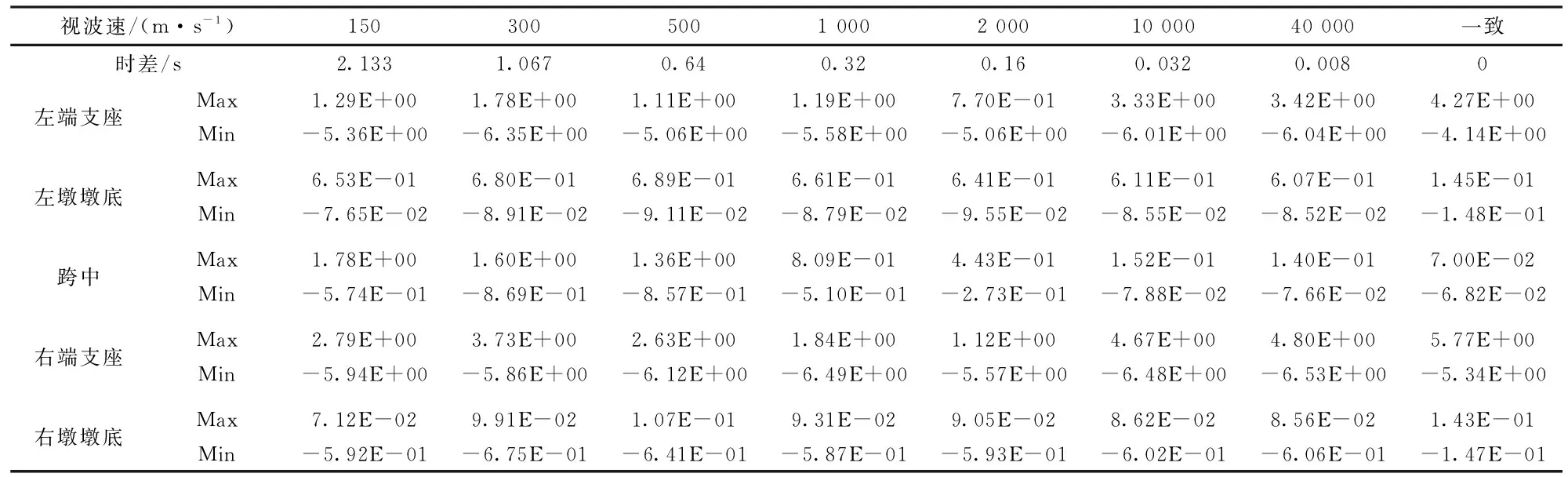
表5 CFRP索斜拉桥行波效应剪切应力 MPa

应力时程曲线如图3所示(以跨中、右支座、右墩墩底为例进行说明)。

图3 CFRP索斜拉桥行波效应应力时程曲线

4.2 结果对比分析

(1) 从位移最大值结果上看,与一致激励的计算结果相比,考虑行波效应后,在横向位移结果中,左塔左侧关键截面大部分正向位移均减小或无明显增加,反向位移大部分为大范围的增大,左塔右侧各截面处正向位移均较为明显的增大,而反向位移除跨中外,其余各截面反向位移均比一致激励条件下的位移减小。跨中位移无论正反方向,均比一致激励条件下位移值大。而对于纵向位移,各截面考虑行波效应之后均比一致激励条件下位移值明显增大。因此,对于CFRP索大跨度斜拉桥地震响应分析,必须考虑纵向地震波作用下的行波效应的影响。

(2) 从关键截面位移时程曲线图中可以看出,桥梁各处相同视波速下的桥梁各处位移大致趋势相同,均较一致激励有明显的差别;同一位置在不同视波速作用下大致趋势相同,但是随着视波速的增加,波动幅度从大变小,当行波波速达到一定程度时,结构的地震时程分析结果与一致地震动输入下的结果基本吻合,一方面说明此时可忽略行波效应的影响,同时也证明了位移输入法在计算行波效应时的可行性;考虑行波效应之后,结构部分位移增长非常显著,因此在设计中按照一致激励进行计算设计偏于保守,在大跨度桥梁的设计分析中必须考虑行波效应的影响。

(3) 分析应力结果表,可以得到,除两支座处,其余各截面轴力无论正向或是反向,大部分均较一致激励增大,支座处反向轴力明显增大,而正向轴力虽减小,但是减小的幅度较小。而剪应力除跨中截面外,其余截面不同视波速应力增大或减小没有明显的规律,而跨中三个截面,不同视波速下的剪应力均增大。因此,行波效应对CFRP索斜拉桥地震响应有显著的影响,但不同截面影响差异较大。

(4) 从关键截面应力时程曲线分析可以得到,同一截面处,不同视波速地震波对其影响应力变化图大致趋势相似;随着地震视波速的增加,斜拉桥地震响应逐渐增加直至趋于一致激励下的地震响应。主梁内力某一视波速时超过一致激励下的主梁内力剪力,但最后均会趋近于一致激励时的地震响应。行波效应对轴力影响比对剪力的影响更为明显。

5 结束语

CFRP索斜拉桥多点激励与一致激励相比,行波效应的存在使得该桥的时程曲线发生了较显著的变化,使塔根的效应增加显著;当行波波速达到一定程度时,结构的地震时程分析结果与一致地震动输入下的结果基本吻合,一方面说明此时可忽略行波效应的影响,同时也证明了采用位移输入法模式在计算行波效应时的可行性;与考虑行波效应的斜拉桥主梁和桥塔抗震设计相比,一致激励下斜拉桥的抗震设计偏保守,但在中视波速阶段桥塔和主梁截面内力会大于一致激励,因此在抗震设计要根据实际视波速来判断行波效应对斜拉桥地震响应的影响。

此外,相比于钢索斜拉桥,采用CFRP索后能减小主梁的最大内力值和最大位移,可以减小主梁的材料用量,节约成本;能减小索塔中的控制内力值和最大位移,改善结构的受力状态;桥梁的变形特征基本接近。因此,相对于钢索斜拉桥,CFRP索斜拉桥在抗震性能方面体现一定的优势,为CFRP索在大跨度的斜拉桥中的应用提供理论参考。

CFRP索的推广应用对大跨斜拉桥抗震性能的提高具有重要的参考价值, 然而CFRP 索也有如锚固难、造价高以及颤振临界风速低[12]等不足之处,这需要进一步的探讨和研究。

[1] 李晓莉.CFRP材料在超大跨度斜拉桥拉索中的应用研究[J].武汉理工大学报，2006, 28(2):30～33.

[2] 项海帆.斜张桥在行波效应作用下的地震反应分析[J].同济大学学报,1983(2):1～9.

[3] 陈幼平,周宏业.斜拉桥地震破坏的计算研究[J].地震工程与工程振动,1995,15(3):127～134.

[4] Nazmy A S,Abdel-Ghaffar A M.3-D non-linear seismic behavior of cable-stayed bridge[J].Journal of Structural Engineering,1991,117(17):24～27.

[5] Abdel-Ghaffar A M,Nazmy A S.Cable-stayed bridge under seismic action recent development and their future[J].Journal of structural Engineering,1991,117(11):24～27.

[6] Nazmy A S,Abdel-Ghaffar A M.Effects of ground motion spatial variability on the response of cable-stayed bridge[J].Earthquake Engineering & Structure Dynamics,1992,21(8):1～20.

[7] 张翠红.大跨度斜拉桥多点激励效应研究[D].南京：东南大学,2004.

[8] 武芳文.超大跨度斜拉桥考虑行波效应的地震动随机响应研究[J].地震学报，2010(3):193～202.

[9] Soneji B B,Jangid R S. Passive hybrid systems for earthquake protection of cable-stayed bridge [J]. Engineering Structures,2007(29):57～70.

[10] 周士金，刘荣桂，蔡东升，等.CFRP索大跨斜拉桥的非线性地震响应控制分析[J].中国公路学报，2011,24(3):64～71.

[11] 张新军,应磊东.超大跨度CFRP 索斜拉桥的力学性能分析[J].公路交通科技，2008,25(10):74～78.

[12] 卢鹏程,应磊东. 碳纤维索(CFRP)斜拉桥的抗震性能分析[J].建筑技术，2010,41(1):60～63.

2016-09-06；修改日期：2016-09-22

安徽省高校自然科学研究项目(KJ2016A448)

杨吉新(1964-)，男，湖南永州人，博士，武汉理工大学教授．

U441.3

A

1673-5781(2016)05-0649-05