悬索线型拱轴线在大跨度拱桥的应用讨论
2016-06-05卢元刚王胜男
卢元刚, 高 磊, 王胜男
(1.安徽省交通规划设计研究总院股份有限公司,安徽 合肥 230088;2. 安徽六安飞宇建设工程有限公司 合肥分公司,安徽 合肥 230088)
悬索线型拱轴线在大跨度拱桥的应用讨论
卢元刚1, 高 磊1, 王胜男2
(1.安徽省交通规划设计研究总院股份有限公司,安徽 合肥 230088;2. 安徽六安飞宇建设工程有限公司 合肥分公司,安徽 合肥 230088)
基于大跨径等截面拱桥的恒载分布更接近于沿拱轴均匀分布,该文推导了拱轴线的新型公式——悬索线拱轴线方程,并结合工程实例进行实桥分析计算,计算结果表明拱圈应力均匀性,验证悬索线型拱轴线在大跨度拱桥中应用价值。
拱轴线; 悬索线; 拱形参数;应力
1 概 述
1.1 常用的拱轴线样公式
各类拱桥,选择拱轴线的原则,是尽可能地降低由于荷载产生的拱圈内弯矩值。最理想的拱轴线是与拱上荷载作用下的压力线吻合,这时拱圈截面只受轴向压力,而无弯矩作用。但事实上是不可能获得这样的拱轴线的,因为除恒载外,拱圈还要受活载、温度变化和材料收缩等因素作用。由于恒载所占的比重很大,因此以恒载压力线作为设计拱轴线,可以认为基本上是适宜的。
目前,拱桥常用的拱轴线型有圆弧线、 悬链线和抛物线[1-2]。
(1) 圆弧线。在均布径向荷载作用(如水压力)下,拱的合理拱轴线为一圆弧线。常用于20 m跨径以下的小拱桥,其受力示意如图1所示。
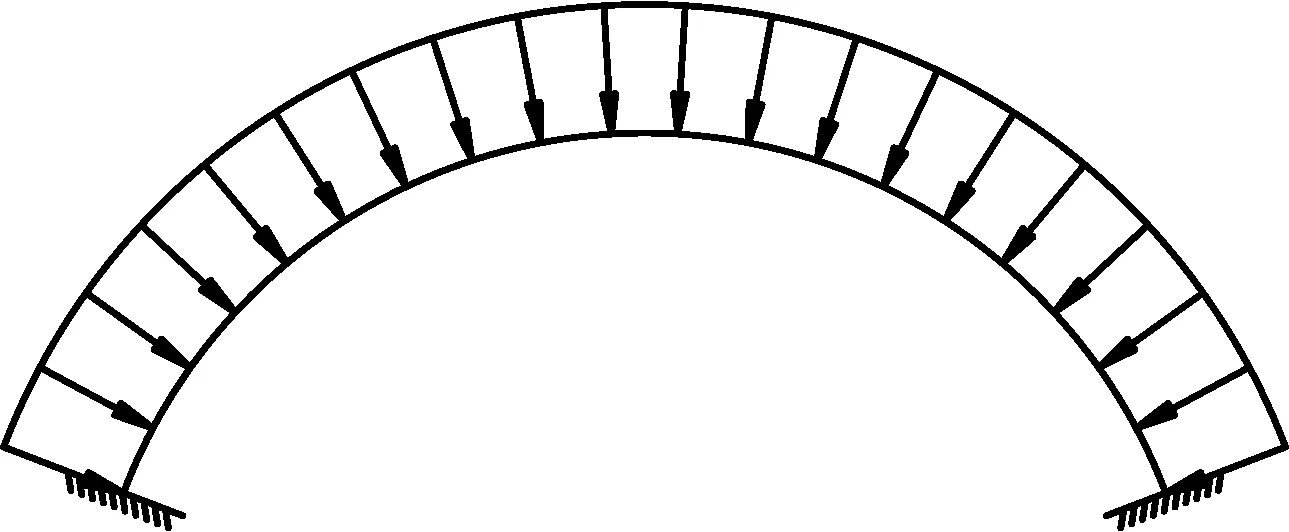
图1 圆弧线型拱轴线受力简图
(2) 悬链线。实腹公式拱桥的恒载集度,从拱顶向拱脚均匀增加,这种荷载分布图公式的拱圈压力线是一条悬链线,因此实腹公式拱桥常采用悬链线作为拱轴线,其受力示意如图2所示。
(3) 抛物线。在沿跨径均布荷载作用,拱的合理拱轴线为二次抛物线,对于恒载集度比较均匀的拱桥,往往使用二次抛物线作为拱轴线,其受力示意如图3所示。
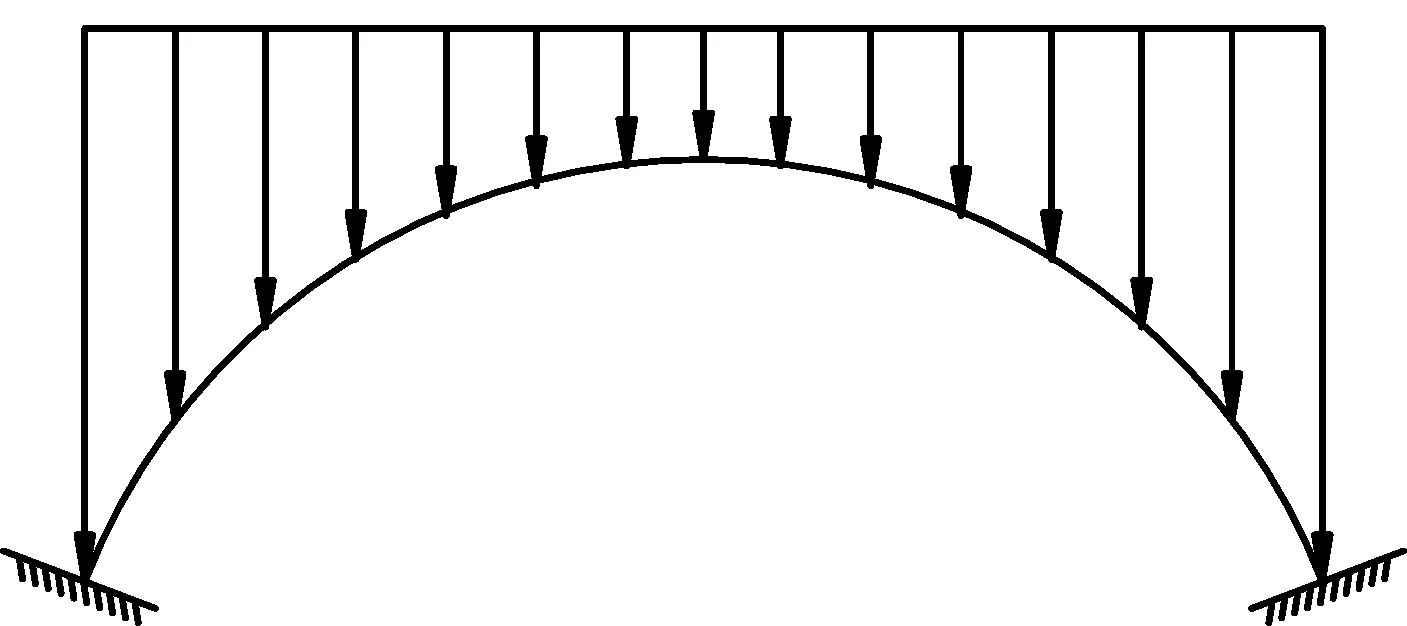
图2 悬链线受力简图
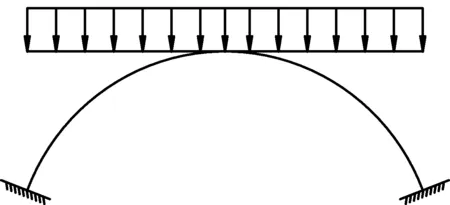
图3 抛物线型拱轴线受力简图
1.2 新型拱轴线——悬索线的提出
对于大跨径,其恒载分布接近于沿拱轴均匀分布,由于已有拱轴线线型无法直接反映这种荷载形公式,因此,该种情况下的合理拱轴线线型及其应用是一个值得研究的问题。本文结合实际工程建议可选择悬索线作为桥梁拱轴线,其受力示意如图4所示。
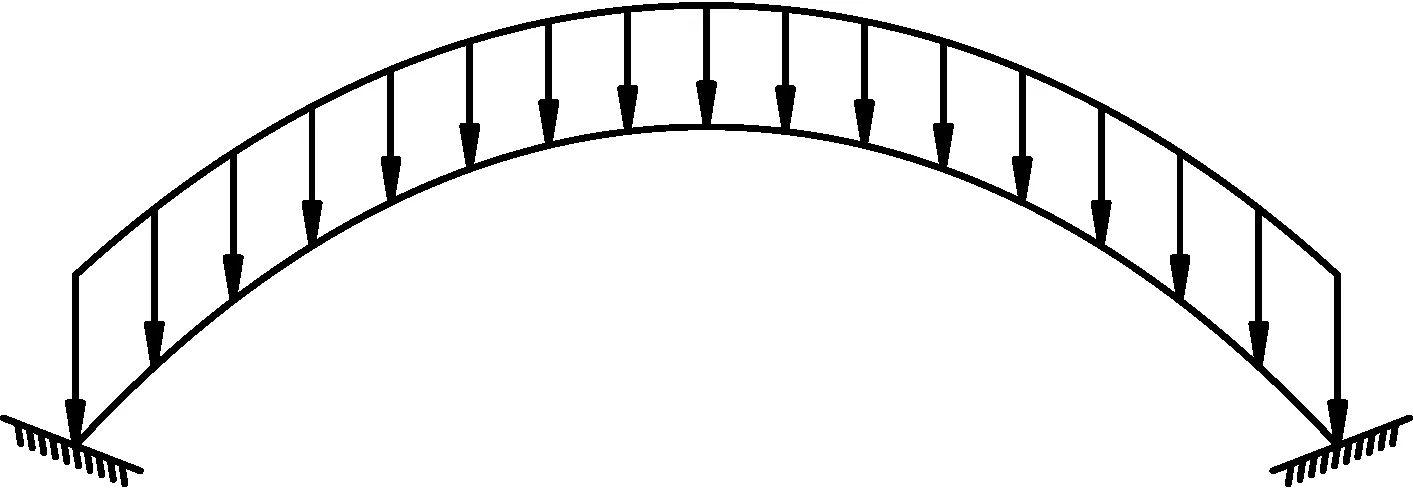
图4 悬索线型拱轴线受力简图
2 悬索线型拱轴线
2.1 悬索线方程推导
设如图5所示半跨拱桥,不计弹性压缩,若作用沿拱轴线均布的荷载w,其拱轴线为恒载压力线,故在恒载作用下拱顶截面处弯矩M=0,由于对称性剪力Q=0,只作用有恒载推力Hg。
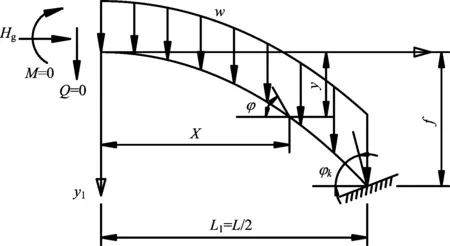
图5 悬索线拱轴线计算图示
以拱顶为原点建立坐标系,水平向为x轴,竖直向下为y1。
对拱脚取矩,可得
(1)
其中,∑Mj为半拱恒载对拱脚的弯矩;Hg为拱的恒载水平推力(不计弹性压缩);f为计算矢高。
对任意截面取矩,因考虑理想拱轴线,假设任意一截面上不存在弯矩,由ΣM=0,y1Hg-Mx=0,得出
(2)
其中,Mx为任意截面x以左全部恒载对x截面的弯矩。
将上述方程二次求导,
(3)
沿x轴的恒载集度gx与沿拱轴线本身的恒载集度w之间有如下关系:
gxdx=wds得出:
(4)
将上述公式带入(3)可得
上述微分方程的解为
(5)
其中,D1,D2为两个为积分常数。
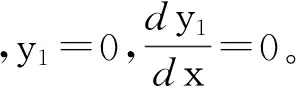
将以上两个条件带入(5)可得
由上公式,可解得
带入(5),得
(6)
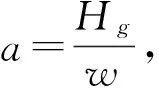
(7)
(7)式即为与假设荷载形公式对应的合理拱轴线方程。
(7)式是按照合理拱轴线的概念得到,它与一条两端支承的链索在单位弧长作用的荷载为常数w时所形成的曲线方程一致, 不过需要将链索形成的曲线绕水平轴旋转 180°。这是因为拉索为柔性索,在自重作用下各截面的弯矩为零,而合理拱轴线是通过使线上各点的截面弯矩为零确定的。柔性索本身的特性恰好满足合理拱轴线的要求。因此, 这种新的拱轴线型称为悬索线,(7)式称为悬索线方程[3-4]。
2.2 拱形参数a的确定
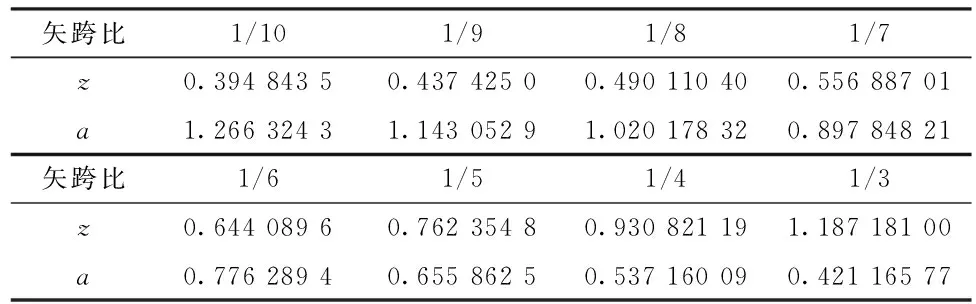
从悬索线方程可知,拱轴形状由参数a唯一确定,不妨将其称为拱形参数。下面首先介绍拱形参数a的确定。建立如图6 所示坐标系, 引入边界条件:
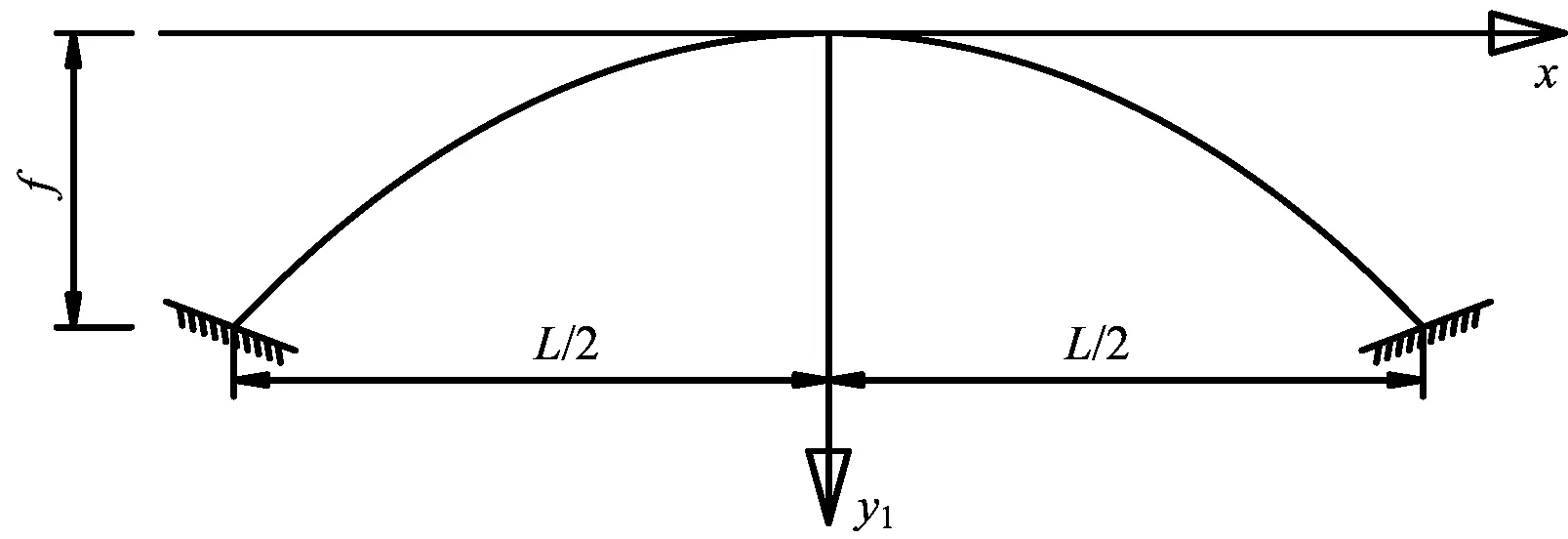
图6 悬索线坐标系
和y1=f
(8)
代入(7)式
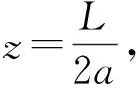
(9)
用迭代法对上述方程求解,其迭代步骤如下:
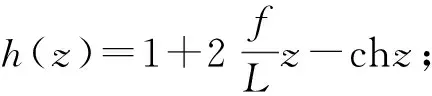
(10)
② 给定2个迭代初始值z1、z2,使得h(z1)、h(z2)异号。
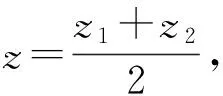
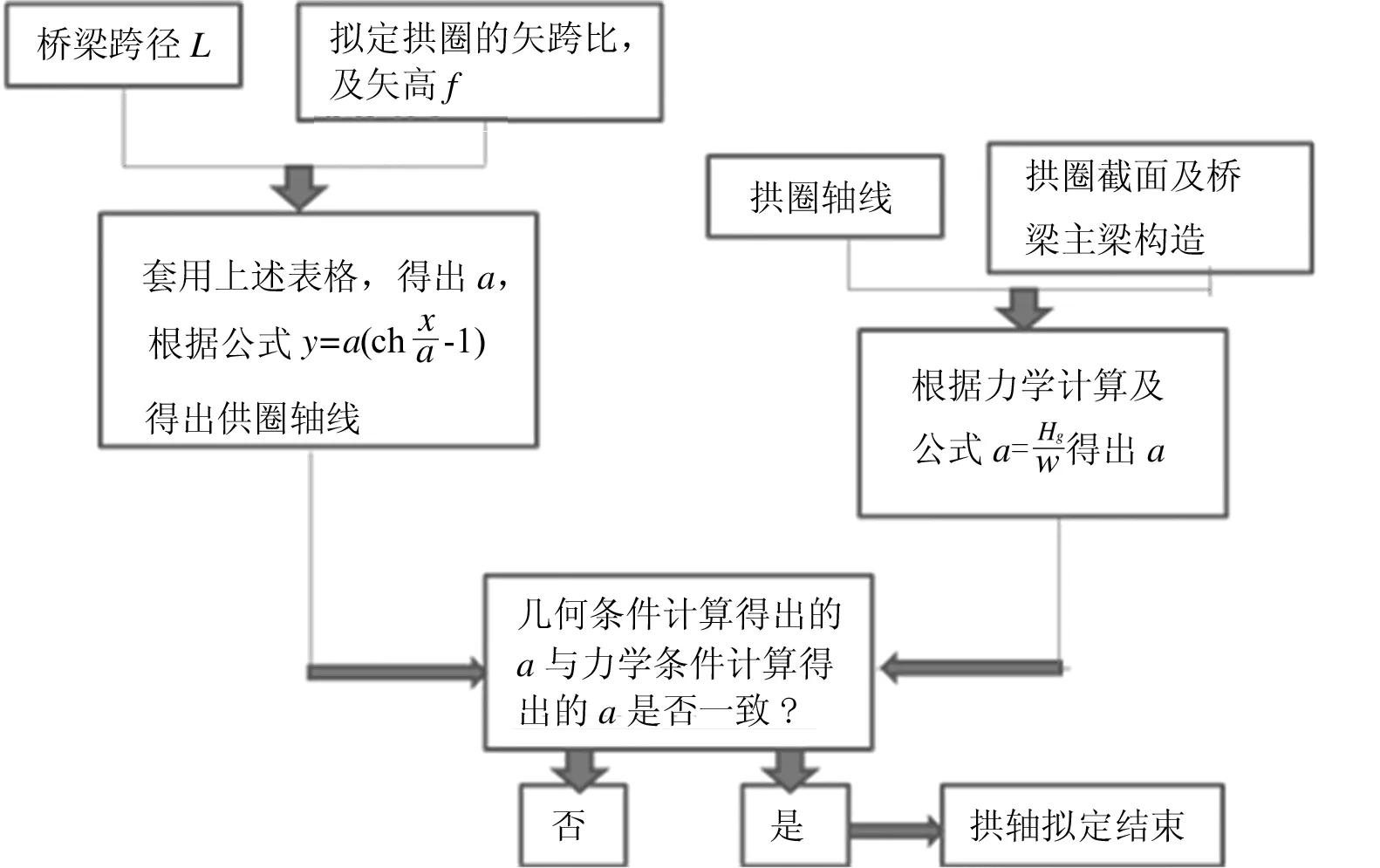
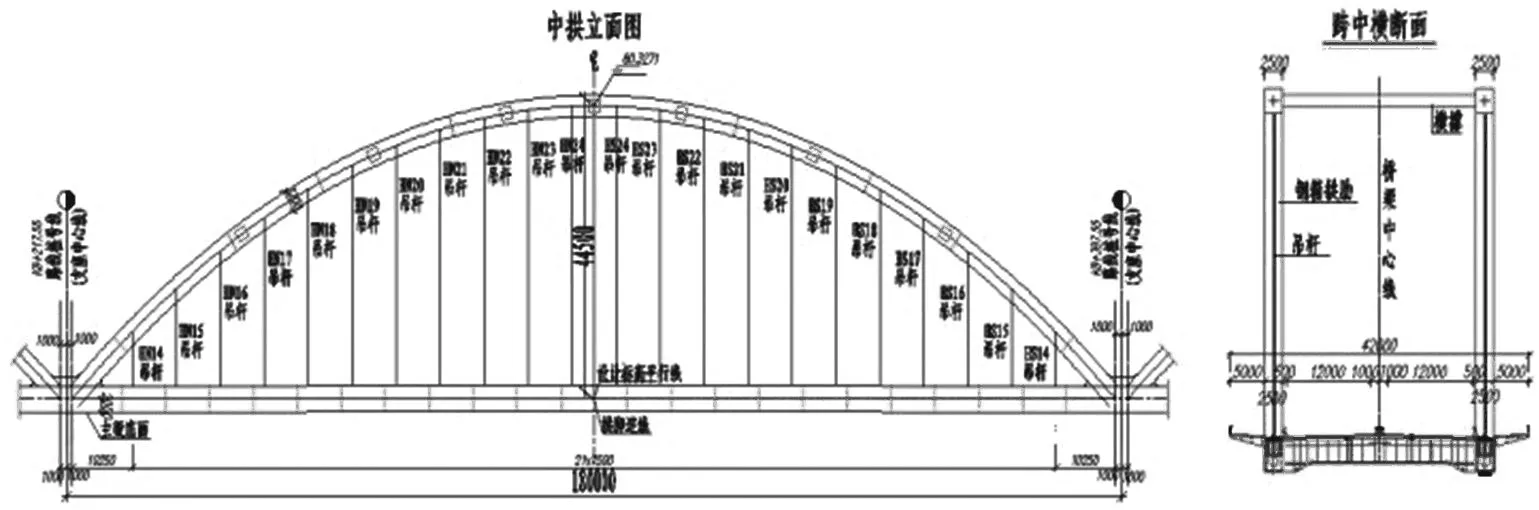
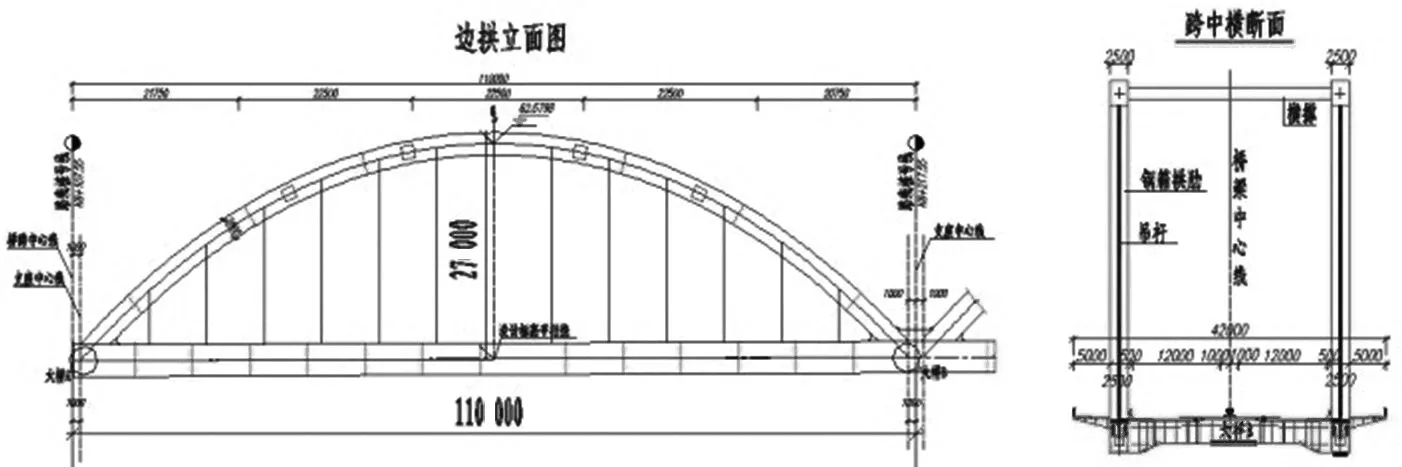
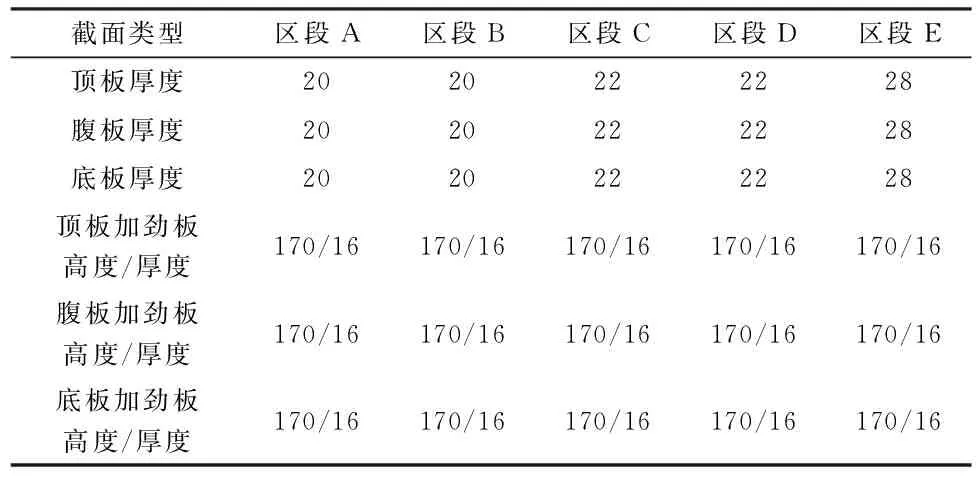
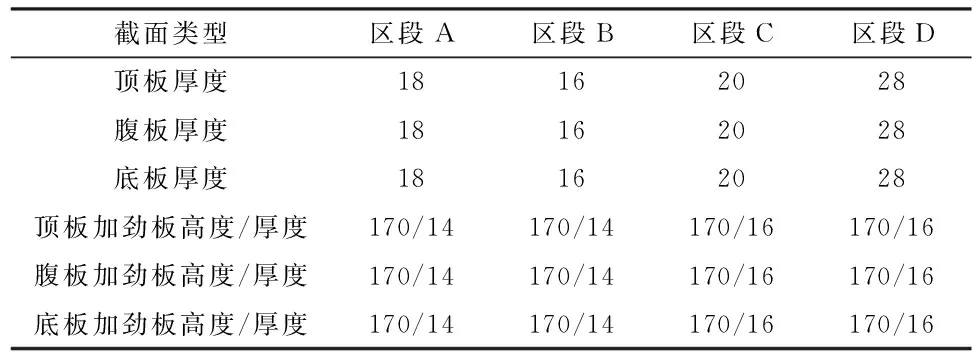
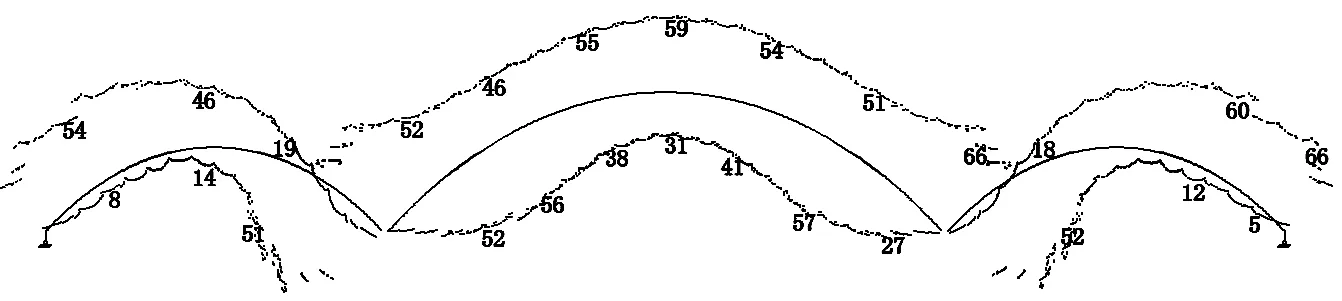
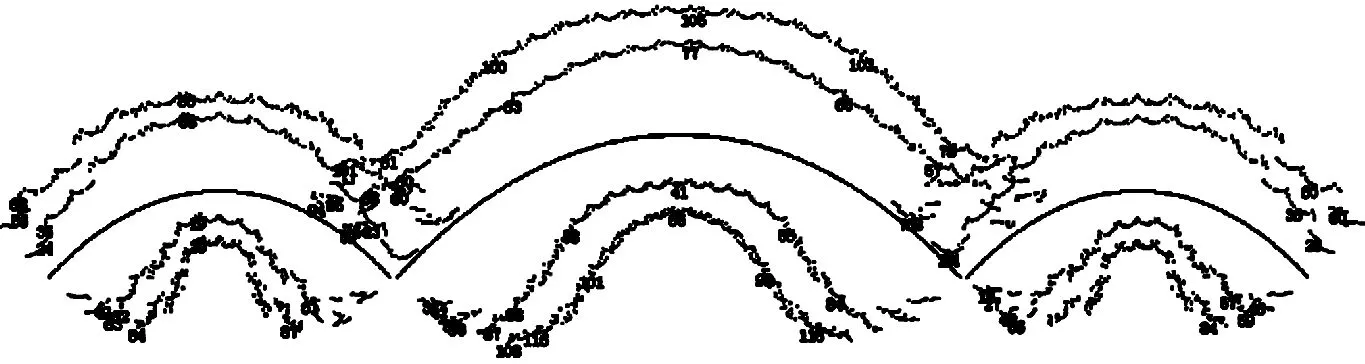
④ 若h(z1)与h(z2)同号,则z1=z;若h(z1)与h(z2)同号,则z2=z,重复第3步,直至h(z1)-h(z2) 从上面的分析中看出,拱形参数a不仅与矢高和跨径的相对比值有关,而且与跨径的数值也有关。用迭代法确定 z 的值时,只要已知拱桥的矢跨比;但要确定悬索线方程拱形参数 a, 则需要已知拱桥具体的跨径l 和矢高 f。表1列出了单位跨径时与常见矢跨比对应的z 值和a值(令L=1)。 当然,也可根据拱形参数定义a=w/Hg,确定a,但在最初的设计中,w、Hg都是待定的,而拱的跨度和矢高是可以事先确定的, 因此常用方法是根据几何边界条件确定参数a。 表1 常见矢跨比(1/12~1/3)对应的参数z和a(令L=1)[5] 拱轴线参数拟定,见图7所示。 图7 拱轴线参数拟定步骤 3.1 设计概况 孔李淮河特大桥为三跨钢箱下承连续系杆拱桥方案,跨径布置为110m+180m+110m,拱圈轴线采用悬索线(图8)。 图8 淮南孔李淮河大桥总体布置图 拱肋系统由中拱肋、边拱肋及拱顶风撑等组成。中拱顺桥向计算跨径178m,立面矢高44.5m,矢跨比为1/4,拱轴线为悬索线,根据L=178,a=0.537 160 09,主拱轴线方程为: y=44.5-(0.537 16×178)×(cosh(x/0.537 16×178)-1) 横桥向,由双榀拱肋组成,拱肋间距为29.5m,中拱(图9)设置7道风撑。 图9 中拱立面图 两侧边拱(图10)计算跨径108m,立面矢高27m,矢跨比为1/4,拱轴线为悬索线,根据L=108,a=0.537 160 09,得出边拱轴线方程为: y=27-(0.537 16×108)×(cosh(x/(0.537 16×108))-1) 图10 边拱立面图 中拱肋钢箱高3 200mm,宽2 500mm,顶、底板及纵向加劲肋厚度为变厚度,除拱梁结合段外,共划分为5个区段(表2)。 表2 中拱拱圈断面细部构造表 边拱肋钢箱高2 200mm,宽2 500mm,顶、底板及纵向加劲肋厚度为变厚度,除拱梁结合段外,共划分为4个区段(表3)。 表3 边拱拱圈断面细部构造表 3.2 拱圈计算模型建立 (1) 计算程序:桥梁博士V3.1.0;校核验算:MidasCivil。 (2) 材料参数:拱肋、主梁等钢结构采用Q345qD钢材;吊杆、柔性系杆:采用预应力钢绞线。 (3) 计算荷载:① 一期恒载:包括拱圈、纵梁自重,按实际断面计算,横梁按集中荷载计算。② 二期恒载包括桥面板、桥面铺装、防撞护栏等,合计222.12kN/m。③ 支座沉降:主墩基础取0.02m,过渡墩基础取0.01m计算。④ 汽车荷载:公路-Ⅰ级。考虑横向折减、纵向折减及偏载系数,计算得到横向分布系数为3.681。⑤ 人群荷载:人群荷载标准值为2.5kN/m2,人行道全宽10m。 (4) 施工阶段划分[6]:按实际施工步骤划分施工阶段,模拟钢拱、钢梁组合顶推到位到成桥的主要施工过程,全桥共划分为76个施工阶段。本文只给出拱圈顶推到位后,桥面板及其他二期恒载施加桥拱圈应力,和全桥正常使用阶段拱圈应力计算结果[7]。 3.3 拱圈计算结果 (1) 顶推到位,二期恒载施加桥拱圈计算结果。拱圈顶推到位后,二期恒载施加前,拱圈应力如图11所示。 图11 拱圈顶推到位后拱圈应力图 拱圈拱顶及拱脚最大压应力均为60MPa,均小于钢箱梁容许应力设计值,且应力较均匀。 (2) 正常使用情况下,拱圈计算结果。在正常使用阶段,标准组合作用下,钢拱圈上、下缘应力如图12所示。 拱圈拱脚最大压应力为118MPa,拱顶最大压应力为105MPa,均小于钢箱梁容许应力设计值[8-10],拱圈拱脚至拱顶应力较均匀,悬索线型拱轴线是合理的。 图12 标准组合下拱圈应力图 通过以上计算结果看出,在拟定矢跨比的前提下,通过查询常见矢跨比悬索线拱轴参数表,可得出悬索线方程,并实际计算验证了所选定拱轴线合理性。同时因矢跨比是事先拟定的,不同的矢跨比可能也会影响拱圈受力情况,故下阶段应针对具体桥跨研究矢跨比拟定相关问题。 悬索线是等截面无铰拱拱轴线型的一种新型型式。悬索线应用的一大优点是计算方便,这可从其拱形参数a的确定及受力计算中看出。 对于大跨径等截面拱桥,当桥面铺装、 拱上构造的自重与拱肋相比所占比例很小时, 可认为恒载分布近似沿拱轴均匀分布。另外对于施工中常见的裸拱状态,悬索线就是此时的合理拱轴线型。 总之,由于悬索线计算方便,适用于沿拱轴均匀分布的荷载形式, 恰好与大跨径或特大跨径等截面拱桥恒载分布相符,因此悬索线在大跨径或特大跨径等截面拱桥上适用范围广泛, 值得大力推广。 [1] 姜友生.桥梁总体设计[M] .北京:人民交通出版社,2012. [2] 范立础.桥梁工程[M].北京:人民交通出版社, 1996. [3] 陈宝春.钢管混凝土拱桥设计与施工[M].北京:人民交通出版社,1999. [4] 李传习,夏桂云.大跨度桥梁结构计算理论[M].北京:人民交通出版社, 2002. [5] 肖汝诚.确定大跨径桥梁结构合理设计状态的理论和方法研究[D].上海:同济大学,1996. [6] 汪 瑞,吴 冲,苏庆田.九堡大桥连续组合拱桥拱脚节点计算分析[A].第十九届全国桥梁学术会议论文集(下册)[C].北京:人民交通出版社,2010.1054~ 1058. [7] 童 林.悬索线钢管混凝土拱梁组合体系及吊杆张拉计算研究[D].长沙:长沙交通学院,2003. [8] 李国平.连续拱梁结合桥的性能和特点[J].桥梁建设.1999(1):10~13. [9] 叶建龙,孙建渊,石 洞,等.梁拱组合吊杆张拉力的确定及分析[J].城市道桥与防洪,1999,23(1):44~47. [10] 张国栋,张 锋.拱-梁共同作用的桥梁有限元分析[J].三峡大学学报(自然科学版),2001(10):400~412. 2016-08-19;修改日期:2016-08-25 卢元刚(1984-),男,安徽宿州人,硕士,安徽省交通规划设计研究总院股份有限公司工程师. U448.22 A 1673-5781(2016)05-0577-04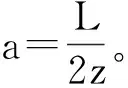
3 应用实例

4 结束语
