B10铜合金高温流变行为及BP神经网络本构模型

韩茂盛，陶 欢

（中国船舶重工集团公司 第七二五研究所，河南 洛阳 471000）

B10铜合金高温流变行为及BP神经网络本构模型

韩茂盛，陶 欢

（中国船舶重工集团公司 第七二五研究所，河南 洛阳 471000）

利用Gleeble-1500D热模拟机对B10铜合金进行热压缩实验，研究了该合金在高温塑性变形过程中的流变应力行为。实验温度为800～950℃，应变速率为0.1～15s-1。研究结果表明，B10铜合金的流变应力随着变形温度的增加而减小，随着应变速率的增大而增大。基于BP神经网络建立了该合金的本构关系模型，预测值与实验值对比表明BP神经网络具有很高的预测精度，所建立的本构模型平均相对误差在1%以内。该模型能够客观真实地描述B10铜合金的高温塑性变形行为，为该合金热变形分析提供基础。

B10铜合金；流变行为；本构关系；BP神经网络

B10合金是以镍、铁为主要合金元素的铜合金，具有优良的耐海水腐蚀性能和抗海生物污损性能，因此广泛应用于舰船、海上石油工程的海水管路系统[1,2]。目前，B10合金主要是以管材及管系附件（如凸缘、法兰等）的形式应用，而其成形方式需要经过高温塑性加工成形[3]。金属热变形流变应力是材料在高温下的基本性能之一，不仅受变形温度、变形程度、应变速率和合金化学成分的影响，也是变形体内部显微组织演变的综合反映，因此，研究材料的高温流变行为是制定热加工工艺的关键。

材料的本构关系是材料的流动应力与变形热力参数之间的函数关系，是联系材料塑性变形行为与各种成形参数的桥梁，在以有限元为代表的现代塑性加工力学中，金属的流变应力值是提高理论计算精度的关键[4,5]。目前，建立材料本构关系时多根据实验数据，借助于回归模型来获得一些经验公式以满足工程技术要求。但是材料的变形过程是一个非常复杂的非线性问题，在实验过程中容易受到各种随机因素的干扰，变形条件与流变应力的关系很难用简单的数学模型准确描述。

人工神经网络具有简单的非线性处理单元的复合映射即可获得复杂的非线性处理能力，不需要给出数学模型，通过对给定的样本数据进行学习，从大量的数据中提取规则，以一组权重形式形成一种网络的稳定状态，然后通过联想记忆和推广能力来获取所需数据。BP算法是普遍使用的一种神经网络学习算法，具有一定的联系容错能力。因此，利用BP算法来建立材料本构关系获得了较为广泛的应用[6-8]。

本文利用Gleeble-1500D热模拟机对B10合金进行高温等温压缩实验，研究其在热变形条件下的流变应力行为，并以不同变形温度、不同应变速率和应变下的等温恒应变速率压缩实验数据作为学习样本，利用BP神经网络建立B10合金的本构关系模型，并对其进行误差分析，为合理制定B10合金热加工工艺提供指导依据。

1 实验

实验用原材料为B10合金铸锭，其化学成分见表1。将铸锭在950℃进行均匀化处理后，加工成ø10mm×15mm的圆柱试样。实验设备采用Gleeble-1500D热模拟实验机，合金的变形温度T分别为800℃、850℃、800℃、950℃，应变速率ε˙分别为0.1、1、10、15s-1，变形量均为60%。以10℃/s的加热速率将试样加热到变形温度，保温3min，变形结束后水淬。

表1 实验合金化学成分（Wt%）

2 B10铜合金高温流变行为

图1为B10合金热压缩变形时的真应力应变曲线。从图中可以看出，当变形温度和应变速率一定时，真应力总体趋势随着应变的增加先迅速增大，随后增大速率减缓，最后基本趋于稳定，这是因为热压缩开始阶段，由于位错的交滑移和攀爬引起的软化不足以补偿由位错密度增加带来的硬化，因此真应力急剧增大；随着变形量的增加，晶粒内参与滑移的可动位错数量增加，软化作用增强，与加工硬化趋于平衡，真应力亦趋于平稳。由图中还能发现，峰值应力及稳态应力随着变形温度的降低和应变速率的提高呈增加趋势，且温度越低，增加的幅度越明显，表明该合金为正应变敏感材料。当变形温度为800℃～850℃时，随着真应变的增加，真应力一直在增加，表明变形过程中动态硬化占主导地位，塑性变形较为困难，因而难以进行变形加工；当变形温度达到900℃以上时，真应力达到峰值后不随着真应变的增加而增大，甚至出现动态软化，特别是应变速率较低、变形温度较高时，应力下降的趋势尤为明显，这一方面是热压缩变形时发生了动态回复和动态再结晶的作用，另一方面由于热压缩变形中的绝热温升现象导致实际温度随着压缩过程的进行有所升高，一定程度上导致了变形抗力的下降。

3 B10铜合金BP神经网络本构模型

3.1 模型建立

BP神经网络即采用BP算法的多层感知器神经网络模型，由输入层、隐含层和输出层组成，其训练过程由信息正向传播和误差反向传播两部分组成，正向传播时，输入信息由输入层经隐含层单元处理后传向输出层，每一层神经元的状态只影响下一层神经元状态。若在输出层得不到希望输出，则转入误差反向传播，将误差信号沿原神经元连接通路返回。返回过程中，逐一修改各层神经元连接的权值，通过上述过程的不断迭代，最终使得信号误差达到允许范围内，网络结束学习训练过程[9-10]。本文采用三层BP神经网络模型，输入层包含变形温度T、真应变ε和应变速率ε˙三个节点，输出层只有一个输出量，为真应力σ，如图2所示。

3.2 数据预处理

图1 B10合金在不同应变速率下热压缩变形的真应力-应变曲线

从真应力-应变曲线中选取624组数据点，其中488组作为训练样本，176组作为检验样本。由于变形温度、变形速率和真应变的数值相差较大，如果同时用于网络的输入节点，势必会湮没小数据对径向函数的作用，造成隐含层与输入层之间权值调节上的困难，从而影响网络的收敛速度和精度，因此根据BP神经网络输入输出规范要求，在建立网络之前必须对所有数据进行归一化处理，使各特征变量在0～1范围内取值，避免网络模型迭代计算时数值过于集中在某些神经元和权值上而降低模型的解算精度，计算公式如下：

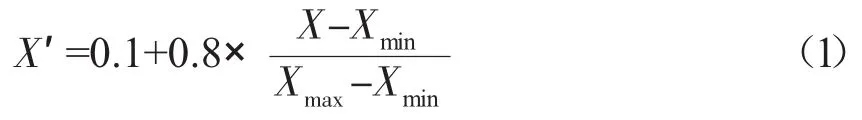
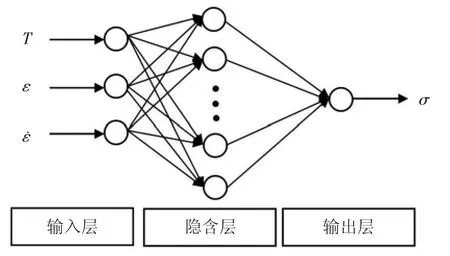
图2 BP神经网络模型

式中，X为实验所获得的原始数据，Xmin和Xmax为原始相应数据的最小值和最大值，X′为参数X归一化处理后的数值。

公式（1）用来归一化温度和流变应力，由于应变已经在0～1之间，不需要归一化处理。但是，由于应变速率变化很大，而且归一化后数值很小，因此，采用公式（2）进行归一化。

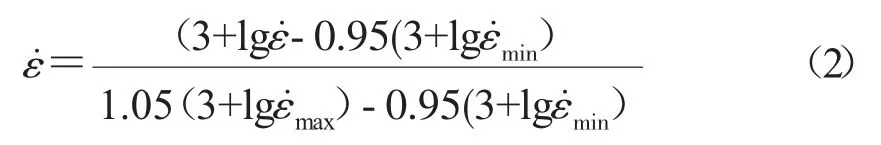
3.3 模型训练

采用Matlab将归一化后的训练样本对BP神经网络进行训练，转移函数为“tan sigmoid”和“pure linear”，训练函数为"Trainlm"，训练目标误差为10-4。在网络模型训练时，隐含层神经元数目的选择是一个至关重要的问题，数目太少会导致训练出来的网络容错性差，不能识别参与未参与训练的样本；数目过多会导致学习时间过长，误差不一定最佳，因此隐含层单元数存在一个最佳值[11]。为了确定隐藏层的神经元的数量，从两个神经元开始，采用试错法进行一一训练，图3为不同隐藏神经元的网络性能。从图中可以看出，随着隐含层神经元个数的增加，网络性能开始呈现显著提高的趋势，当隐藏层存在16个神经元时，具有最小的平均方根误差，因此，一个具有16个神经元的隐藏层用于预测B10铜合金的流变应力。BP网络模型经过1200个循环达到稳定状态。

图3 不同隐含层神经元个数的网络性能

3.4 结果分析

由于BP神经网络预测输出的真应力值在0～1之间，因此需要反归一化处理后才能与实验值进行比较。将公式（1）进行移项处理，并替换其中的相应项，便可得到反归一化运算公式：

式中，σ0为预测真应力值，σmax、σmin为检验样本真应力的最大值和最小值，σn为网络输出的归一化处理后的真应力值。

图4为采用BP神经网络模型预测的B10铜合金流变应力与实验值的对比图，从图中可以看出，采用BP神经网络模型预测的流变应力值与实验值吻合良好，且具有较高的精度。

图5为BP神经网络模型预测的流变应力值与实验值的关联性曲线，从图中可以看出，BP神经网络预测的流变应力与实验数据的相关性较好，拟合相关系数达到0.9999。

对于模型精度的评价，可用平均相对误差表示：

式中，Ei为流变应力的实验值，Pi为通过BP模型计算的预测数据，N为实验分析数据点的个数。经计算，得到平均相对误差为0.56%，进一步证明BP神经网络模型具有较高的精度，可满足工程计算要求。

4 结论

图4 B10铜合金流变应力值与实验值的对比

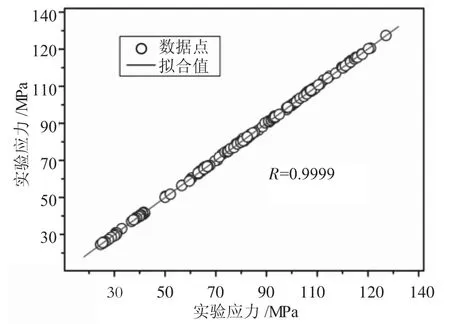
图5 BP神经网络模型预测流变应力值与实验值的关联性曲线

（1）通过热压缩实验得到了B10铜合金在应变速率为0.1～15s-1和变形温度为800～900℃的真应力-应变曲线，发现B10铜合金的流变应力随着变形温度的增加而降低，随着应变速率的增大而增大。

（2）基于实验获得的样本数据，采用BP神经网络模型对样本数据进行训练和预测并进行验证，结果显示计算值和预测值的拟合相关系数达0.9999，得到的平均相对误差在1%以内，表明BP神经网络模型具有较高的精度，能较好地满足工程计算要求。

[1]林乐耘，徐 杰，赵月红.国产B10铜合金海水腐蚀行为研究[J].中国腐蚀与防护学报，2000，20（6）：361-364.

[2]郑俊涛，张三平，周学杰，等.白铜B10和B30冲刷腐蚀对比研究[J].装备环境工程，2010，27(1)：40-42.

[3]王祝堂，田容璋.铜合金及其加工手册[M].长沙：中南大学出版社，2001.

[4]Sha W,Edwrads K L.The use of artificial neural networks in materials science based research[J].Materials and Design,2007, 28:1747-1752.

[5]Mordike B L,Ebert T.Magnesium:properties-applicationspotential[J].Materials Science and Technology,1997,13:210.

[6]田希杰，高 军.基于人工神经网络的冷挤压精度预测[J].锻压装备与制造技术，2007，6.

[7]李慧丽，吴朋越，谢水生.利用BP神经网络预测铜合金挤压力[J].锻压装备与制造技术，2005，2（22）.

[8]Bariani P F,Bruschi S,Negro T.Prediction of nickel-base superalloys'rheologicalbehavior under hot forging conditions using artificial neural networks[J].Journal of Materials Processing Technology,2004,152:395-400.

[9]张兴全，彭颖红.Ti-17合金本构关系的人工神经网络模型[J].中国有色金属学报，1999，9（3）：590-595.

[10]刘学峰，马胜军，刘锦平.Cu-12%Al合金高温压缩变形过程中本构关系的 BP神经网络模型[J].材料工程，2009，1：10-13.

[11]楼顺天，施 阳.基于MATLAB的系统分析与设计-神经网络[M].西安：西安电子科技大学出版社，1998.

High temperature flow stress behavior of B10 copper alloy and BP neural network constitutive model

HAN Maosheng,TAO Huan
（Luoyang Ship Material Research Institute,Luoyang 471000,Henan China）

The hot compression test has been conducted to B10 copper alloy by use of Gleeble-1500D simulator under temperature range from 800℃ to 950℃ andstrain rate range from 0.1s-1 to 15s-1.The flow stress behavior of this alloyduring plastic deformation at elevated temperature has been studied.The experimental results show that the flow stress of B10 copper alloy decreases with the increase of deformation temperature but enhances with the increase of the stain rate.The constitutive relationship model has been built to this alloy on the basis of BP neural network.By comparison between the predicted value with the experiment value,it is shown that BP neural network has high prediction accuracy.The average relative error of the constitutive model is less than 1%.This model can objectively and truly describe the plastic deformation behavior of the B10 copper alloy at high temperature.It provides basis for hot deformation analysisof this alloy.

B10 copper alloy;Flow stress behavior;Constitutive relationship;BP neural network

TG146.1

A

10.16316/j.issn.1672-0121.2016.06.028

1672-0121（2016）06-0112-04

2016-04-27；

2016-06-15

韩茂盛（1987-），男，硕士，工程师，从事材料制备、加工方面研究。E-mail：cfdeng2000@163.com